基于系数搜索的振动补偿在平台重力测量中的应用研究

牟宗磊, 李振飞, 胡 若, 要佳敏, 冯金扬

(1. 山东科技大学 电气与自动化工程学院,山东 青岛 266590; 2. 中国计量科学研究院,北京 100029; 3. 国家市场监管总局时间频率与重力计量基准重点实验室,北京 100029)

地球重力场信息是广泛应用于计量、地球物理、导航制导、资源勘探与国防等领域的重要战略资源[1-3]。绝对重力仪是获取地球重力场信息的重要仪器,随着野外、海洋和航空等领域重力测量需求的增加,平台式绝对重力仪迅速发展[4]。与相对重力仪相比,绝对重力仪不存在零点漂移,无需定期标定和校准,且具有良好的长期稳定性[5]。因此,平台式绝对重力测量在动态环境中具有重要的应用价值。Sokolov等[6]在海上开展了平台式激光干涉绝对重力仪重力测量的研究。浙江工业大学的研究团队[7-8]利用原子重力仪进行了车载静态和动态测量。

在激光干涉绝对重力仪测量过程中,参考棱镜为落体棱镜提供一个惯性参考点,理论上应该相对惯性参考系静止,但是在实际测量过程中,参考棱镜总是会受到地面振动的干扰,导致振动干扰耦合进干涉仪测量到的落体位移中,严重影响重力加速度的测量精度[9-10]。目前,主要采用两种方法减小振动对测量精度影响,一是使用隔振系统,尽可能减少地面振动对参考棱镜的影响;二是建立一套振动补偿方法,通过传感器测量参考棱镜的振动干扰,在后续计算时去除振动对干涉仪测量到落体轨迹的干扰[11-13]。与隔振系统相比,振动补偿方法更适用于复杂的地面静态测量环境或者动态测量环境[14-15]。在振动补偿算法研究方面,Wang等和Qian等提出了简化传递函数模型的振动补偿算法,在不同环境下,利用相关分析法或黄金分割法对时延系数和增益系数进行实时计算,对下落物体轨迹信号进行修正,并给出重力值的实测结果。

与研制重力仪时常见的实验室环境相比,复杂环境的绝对重力测量对平台式绝对重力仪的测量精度提出了不同的要求。以飞行器发射场的重力校准为例,地球重力场信息会影响飞行器的初始定位和飞行控制,进而影响飞行器的落点精度,几十mgal(1 mgal=10-5m/s2)的重力扰动会使得飞行器落点偏差达到千米级。当飞行器落点偏差的限差量在100 m以内时,重力测值的精度应优于4 mgal[16],根据计量学的相关要求[17],可以合理假设该指标指的是包含因子k=2的扩展不确定度。基于保守评估的思想,本文研究能使车载平台重力测量的合成标准不确定度(包含因子k=1)达到2 mgal的振动补偿方法,此时符合该精度要求的测量结果必然全部满足上述指标。

本文基于NIM-3C型激光干涉式绝对重力仪和升降平台搭建了一套模拟车载平台重力测量的试验系统,并在三种不同地面环境上进行试验。利用基于系数搜索的振动补偿方法对实测数据进行处理,经过振动补偿后的重力值测量准确度优于2 mgal。本文的研究成果,有望为提高车载平台绝对重力仪的野外静态、动态测量测量精度提供支持。

1 原理分析

1.1 绝对重力仪工作原理

激光干涉式绝对重力仪以激光波长作为长度基准,以原子钟作为时间基准[18]。角锥棱镜作为落体在真空腔内做自由落体运动,用激光干涉法测量落体的下落距离s,用原子钟同步的时钟信号测量对应的下落时间t。对(s,t)数据进行最小二乘拟合,再进行固体潮、气压、极移等各项修正,得到被测点的重力加速度值,测量精度可以达到微伽量级[19-20]。其测量原理,如图1所示。

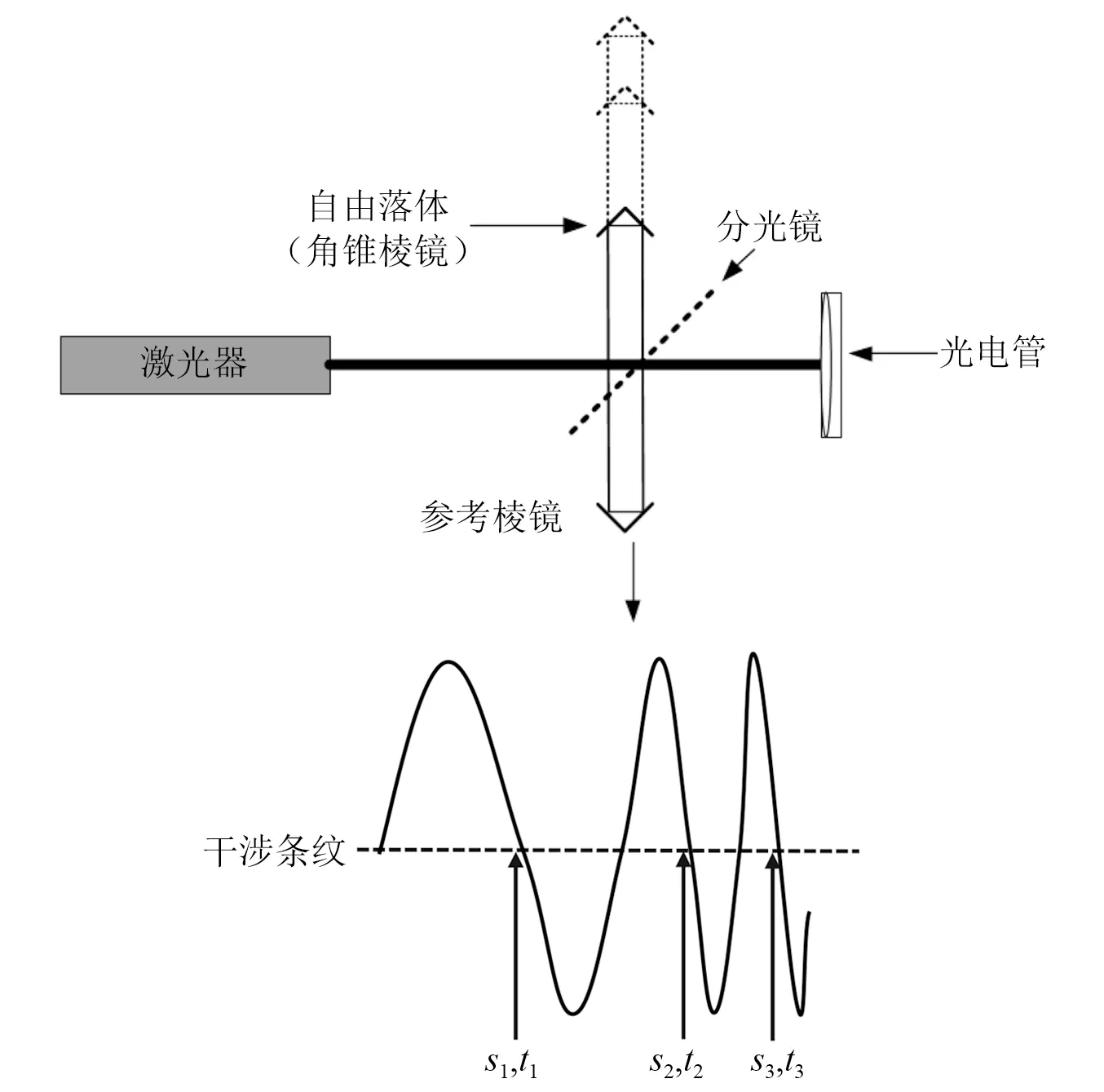
图1 绝对重力仪测量原理图Fig.1 Schematic diagram of the absolute gravimeter measurement

对于激光干涉式绝对重力仪,真空中做自由落体的物体轨迹可以用一个理想的二次函数来表示

(1)

式中:s0,v0为物体自由落体的初始位移和初始速度;g0为要测量的重力加速度;S(t)为t时刻理想的自由落体位移。

1.2 振动补偿原理

在实际测量中,由于参考棱镜受到外界振动的干扰,会给测量轨迹引入振动干扰,激光干涉仪测量到落体的实际运动轨迹为

(2)

式中,N(t)为参考棱镜的运动。

振动补偿的基本原理是在测量落体轨迹的同时使用地震计记录参考棱镜的振动信息,在后续计算时通过算法去除参考棱镜振动的干扰。地震计测量到的振动用Nm表示,由于传感器的敏感结构和参考棱镜是不同的物体,地震计测量到的振动Nm并不等同于参考棱镜受到的实际振动N。因此,提高振动补偿精度的关键是地震计测量到的信号尽可能接近于参考棱镜的真实运动。另外,两者之间存在着一个传递函数关系,Nm和N之间的传递函数G(s)可以表示为

(3)

式中:G1为地面振动V0到参考棱镜振动N的传递函数;G2为地面振动V0到地震计输入的传递函数;G3为地震计的传递函数。

传递函数中G1/G2受重力仪底座的结构、地震计与参考棱镜在底座上的固定方式、地震计与参考棱镜之间距离等因素的影响,并不容易被直接确定。地震计自身的传递函数G3并非幅频特性恒定、相频特性为线性的理想传递函数,有可能会随着测量时间以及环境的变化而发生变化。虽然实际的传递函数不易测量,但是单次测量中测量环境不会发生显著变化。因此,现有的振动补偿算法大多利用一个具有时延系数τ和增益系数A的传递函数模型来简化实际的传递函数G(s)[21],地震计输出Nm与参考棱镜运动N的关系可以表示为

N(t)=ANm(t+τ)

(4)

式中:A为增益系数;τ为时延系数。

修正后的运动轨迹可以表示为

(5)

在求解时延系数时,首先,给定时延τ的搜索范围,通过对位移拟合残差RS和振动位移的拟合残差RN进行相关性分析找出最大相关系数,确定时延τ;再给定增益A的搜索范围,对S′(t)进行二次拟合得到拟合残差R′,遍历搜索使得R′标准差达到最小值对应的增益A。最后,将求得的时延系数和增益系数代入到式(5),计算得到振动补偿后的重力值。

2 试验方法

2.1 试验方案

基于NIM-3C型绝对重力仪、宽频带地震计、升降平台等硬件设备,设计搭建了一套模拟车载升降平台的绝对重力测量系统。在三种不同的地面环境进行了试验,并验证上述程序的振动补偿效果,试验地点为中国计量科学研究院昌平院区。

NIM-3C是中国计量科学研究院自主研制的可移动式绝对重力仪,可适用于车载及野外环境[22]。地震计选用的是加拿大nanometrics公司生产的Trillium120型速度传感器,带宽为0.008 3～150 Hz,灵敏度为1 200 V/(m/s)。升降平台是模拟车载工况的装置,高度1.82 m,重力仪的干涉仪和真空筒三脚架固定在升降平台上。在实际车载工况中,当车辆停在测量地点后,为避免测试车辆轮胎引入振动,使用升降平台将重力仪和车辆进行分离。本次试验在三种不同的地面环境进行,试验现场如图2所示。

图2 试验现场Fig.2 Test site

2.2 试验前期准备

在进行重力值测量前,由于当前模拟车载升降平台的振动频率带宽未知,因此在正式采集干涉条纹信号和地震计信号前,先使用加速度计搭建了一套振动测量装置,确认三种工况下落过程中参考棱镜附近的振动情况。本文选用了河北美泰电子科技公司生产的MSA1000A-02型加速度计,灵敏度为1 000 mV/g,-3 dB带宽为10～800 Hz,量程为±2g(g=9.8 m/s2),可以适应较强振动干扰及移动平台环境。

采集参考棱镜处的振动信息时,将控制电机运动的外触发信号分出一路接入振动数据的采集仪器上,在控制落体下落的同时,触发加速度计采集参考棱镜处的振动信息。对应自由落体时间范围的振动数据频域信息,如图3所示。

图3 参考棱镜处振动频域信号Fig.3 Vibration frequency domain signal at retro-reflector

由图3可知,参考棱镜的振动主频在150 Hz以内,因此选用的地震计符合试验要求。

3 试验结果及分析

本次试验采集了三种工况下各100次下落的试验数据,以办公室大厅的试验结果为例。落体棱镜在真空中自由下落时,干涉仪和地震计记录到激光干涉条纹信号和振动信号,通过对下落位移信号进行二次拟合,可以得到每次下落轨迹的拟合残差RS,振动数据经二次拟合得到残差RN,结果如图4(a)所示。通过截取不同时间段的振动信号计算两者的相关性并找出最大相关系数,结果如图4(b)所示。根据最大相关系数求得时延系数,结果如图4(c)所示。计算增益时,设定初始增益A0为1,步长d为0.01,100次下落数据计算得到的增益系数,结果如图4(d)所示。

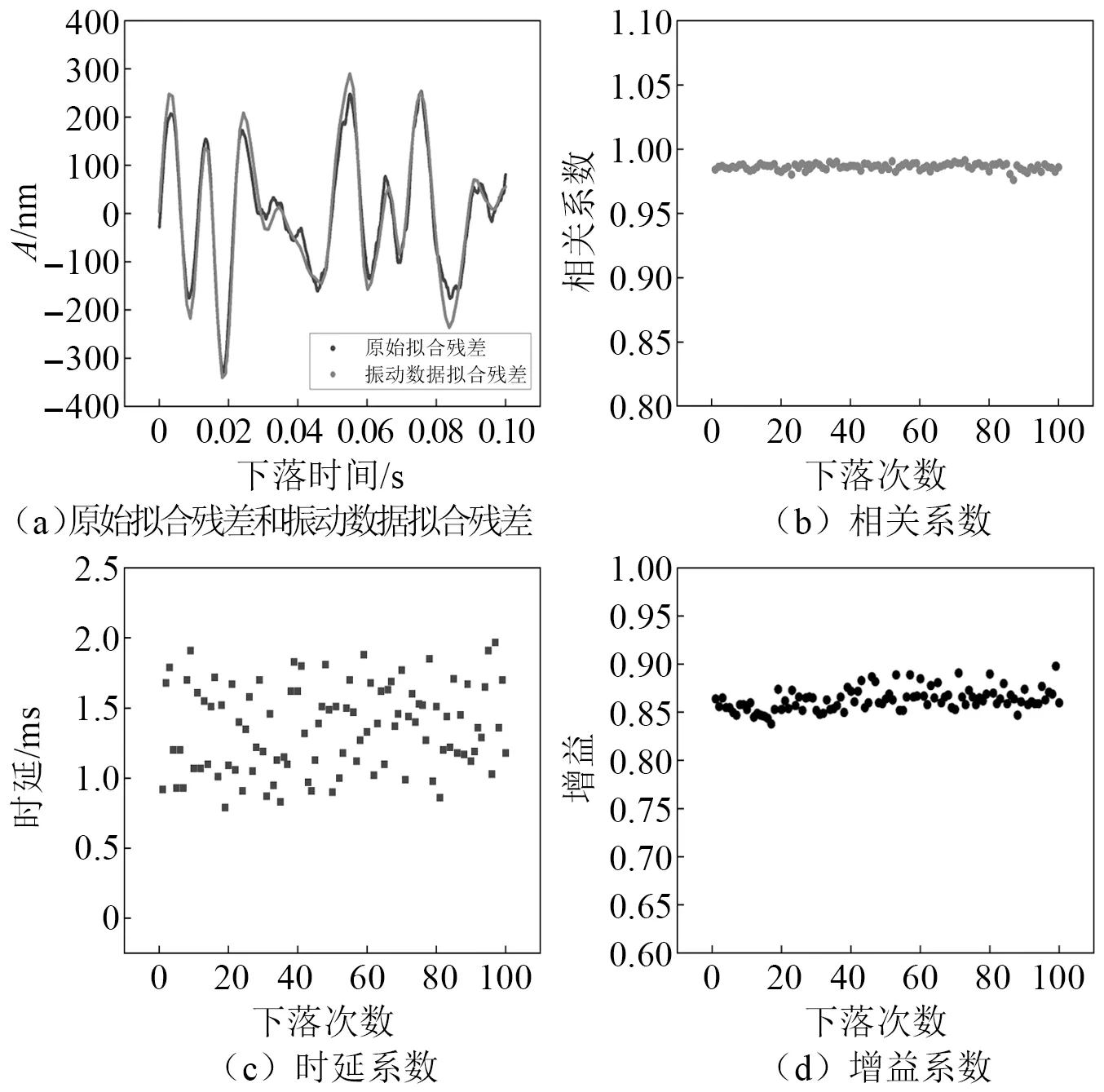
图4 数据处理结果(办公室大厅)Fig.4 The results of data processing(Office hall)

在此试验工况下,100次下落数据的最大相关系数平均值为0.99,相应时间延迟τ的平均值为1.36 ms,标准差为0.3 ms,增益A的平均值为0.86,标准差为0.012。如前所述,理论上试验环境及试验条件不变时时间延迟和增益的真值应该保持不变。因此,选用100次下落数据时间延迟系数和增益系数的平均值进行振动补偿。

将2017年在中国计量科学研究院举行的第十届国际绝对重力仪关键比对ICAG-2017中测量点位的重力值作为参考真值,通过相对重力仪引值到试验位置,得到室内办公室大厅的重力参考真值g0为98***0.7 mgal,室外方砖地面的重力参考真值g1为98***0.8 mgal,室外柏油地面的重力参考真值g2为98***0.8 mgal。室内地面环境振动补偿前后的拟合残差和重力值,如图5所示。

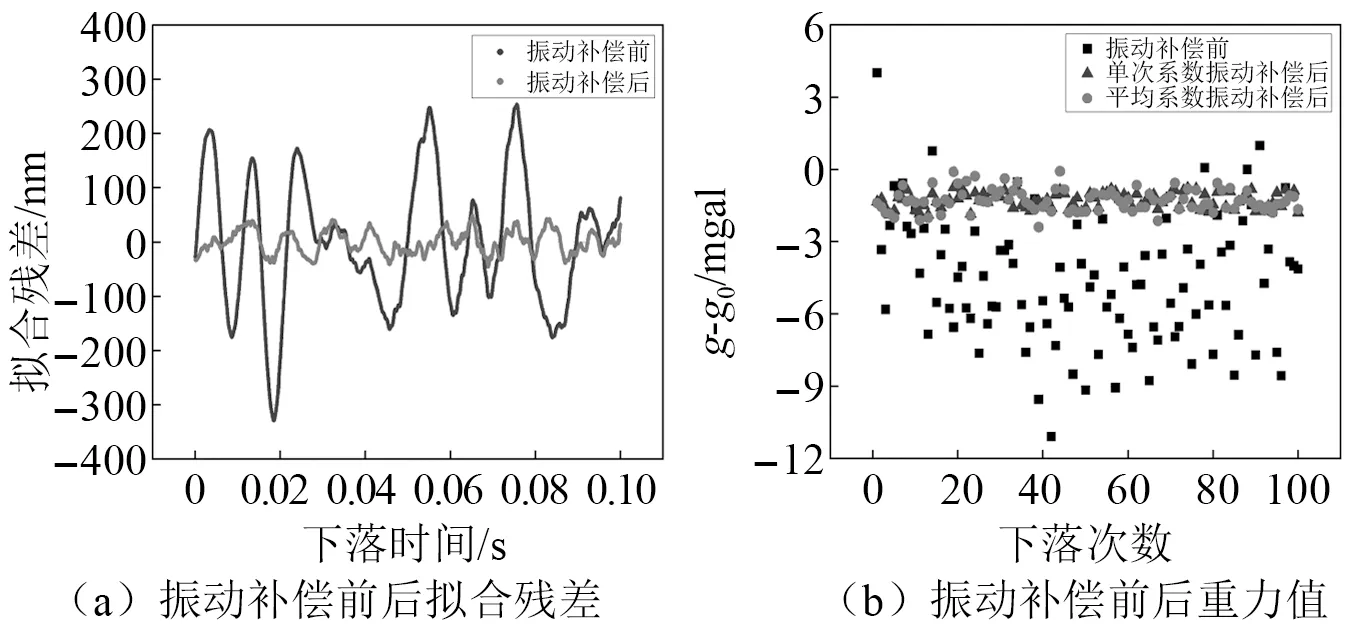
图5 振动补偿前后重力值和残差(办公室大厅)Fig.5 Gravity values and residuals before and after vibration correction(Office hall)

其中,室内地面环境振动补偿前重力平均值为98***6.1 mgal,标准差为2.64 mgal;单次下落数据搜索得到的系数进行振动补偿后重力平均值为98***9.4 mgal,标准差为0.32 mgal;100次下落数据搜索得到的平均系数进行振动补偿后的平均值为98***9.4 mgal,标准差为0.45 mgal,单次下落经过振动补偿后的拟合残差也得到了修正。用单次下落数据搜索得到的系数进行振动补偿的结果和100次下落的平均系数进行振动补偿的结果差异不大,再次说明系数的平均值确实可以作为真值的合理估算值,因此后续使用系数的平均值进行振动补偿。

室外两种地面环境振动补偿前后的重力值结果,如图6所示。

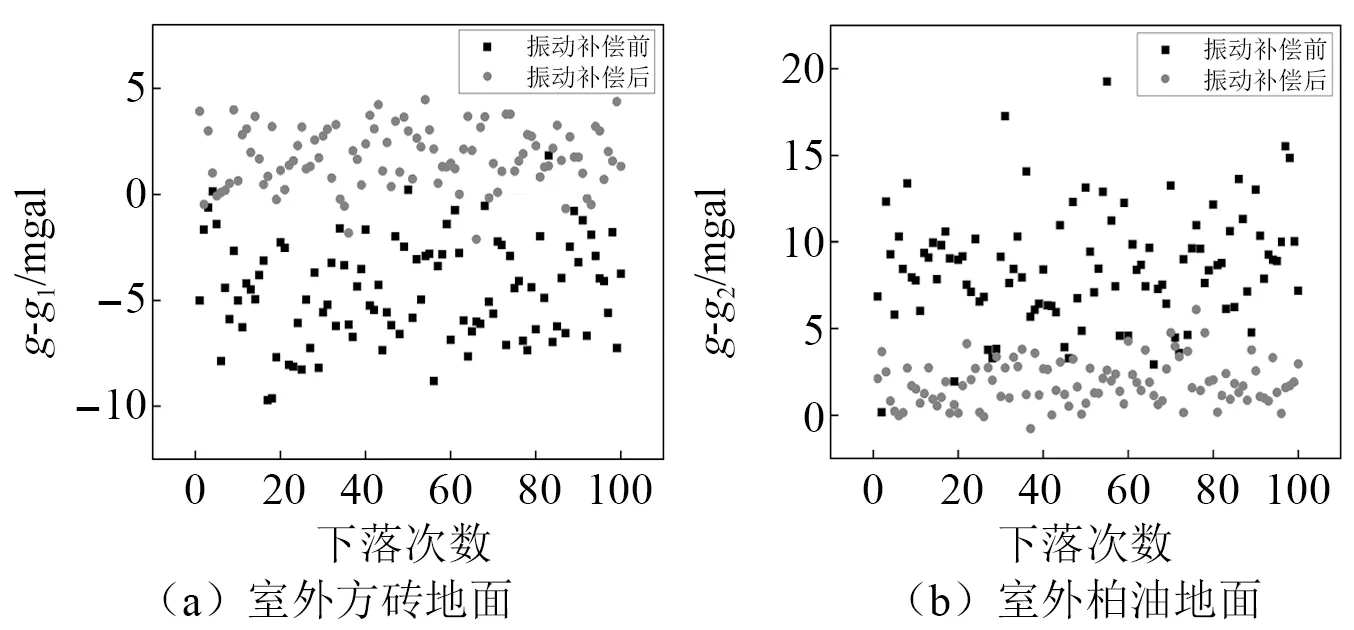
图6 室外地面环境振动补偿前后重力值Fig.6 Gravity values before and after outdoor ground environment vibration correction

其中,室外方砖地面环境振动补偿前重力平均值为98***6.3 mgal,标准差为2.36 mgal;振动补偿后的平均值为98***2.6 mgal,标准差为1.39 mgal。室外柏油地面环境振动补偿前重力平均值为98***9.4 mgal,标准差为3.22 mgal;振动补偿后的平均值为98***2.7 mgal,标准差为1.28 mgal。

三种工况下的试验结果,如表1所示。

表1 三种地面工况试验结果对比Tab.1 Comparison of test results under three ground conditions

计算时,时延系数和增益系数使用的均为平均值。由表1对比分析可知,在室内环境中,通过振动补偿算法,可以将重力值标准差减小83%,跟重力参考值的差值减小到-1.28 mgal。室外两种地面环境,经振动补偿后,方砖地面重力值标准差减小41%,跟重力参考值的差值改善为1.76 mgal。柏油地面重力值标准差减小60%,跟重力参考值的差值减小到1.86 mgal。在三种不同试验工况下,经过振动补偿算法的后处理,重力值均能够满足2 mgal的测量准确度。

4 结 论

本文基于NIM-3C型光学绝对重力仪搭建了一台模拟车载升降平台绝对重力测量系统,介绍了绝对重力仪的工作原理和基于系数搜索的振动补偿方法,评估了自由落体过程中试验环境的振动情况。在重力测量过程中,使用地震计记录振动信号,计算原始位移拟合残差和振动数据的拟合残差相关系数最大值得到时延系数。使用遍历法来计算增益系数,以单次下落拟合残差标准差的最小值来确定增益,对测量结果进行振动补偿后处理。试验结果表明,基于系数搜索的振动补偿算法在三种不同地面工况下均有良好的效果。在室内地面工况下,振动补偿后能将重力值的标准差减小83%,在室外地面工况下,经过振动补偿后,方砖地面重力值标准差减小41%,柏油地面重力值标准差减小60%。振动补偿后的重力值均能够满足2 mgal准确度要求。

随着绝对重力仪技术的发展,适用于野外定点观测甚至动态平台的绝对重力仪需求正在迅速增加,振动补偿技术也正朝着适应高动态测量环境的方向发展。本文的研究成果可以为后续平台式绝对重力仪开展野外静态、动态测量提供支持。