二阶主共振下旋转叶片振动抑制器稳定性研究

宋 洋, 张 博, 陈旭东, 丁 虎, 陈立群

(1. 上海大学 力学与工程科学学院,上海 200444; 2. 长安大学 理学院,西安 710064; 3.西安热工研究院有限公司,西安 710054)

旋转叶片是燃气轮机的核心部件,其在工作过程中常常因为内共振而发生大幅的有害的振动,导致其损坏,进而令燃气轮机无法正常使用。主动控制作为一种精准有效的减振措施,受到国内外学者的广泛关注。

一直以来都有学者针对旋转叶片的非线性动力学行为进行了研究,通常将旋转叶片建模为梁、板或壳。Yao等[1]利用多尺度法获得了1∶2内共振情形下的自治演化方程,并给出不同参数下数值模拟的相位图、波形和功率谱,说明了旋转叶片同时存在周期性与混沌运动。Karimi等[2]将叶片建模为Eular-Bernoulli梁,用摄动法研究了自由振动的旋转叶片在三种不同内共振条件下的运动情况,揭示了不同模态之间的能量转移现象。Zhang 等[3]用多尺度法得到了1∶2内共振条件下考虑预变形的旋转叶片的演化方程,研究了参数变化对系统响应的影响,揭示了叶片运动过程中的跳跃现象和饱和现象。Zhang等[4]将亚音速气流激励下的旋转预扭转的复合材料叶片视作一个复合悬臂矩形板,利用三阶剪切变形板理论von-Karman型非线性理论和Hamilton原理,推导出了叶片的控制方程。李红影等[5]针对壳板凸肩叶片,应用Donnell’s简化壳理论建立了其非线性振动微分方程,并用伽辽金法对方程离散化,又用平均法分析了模态方程组。Roy等[6]将旋转叶片建模为Timoshenko梁,分析了系统参数对固有频率和系统响应的影响。文献 [7-12]用对叶片不同内共振情形进行了研究,探索出了叶片的非线性动力学行为。

有关旋转叶片的振动控制也吸引着很多学者的关注。主动控制具有附加质量小的优点,适合用于旋转叶片高温高压特殊的工作环境。智能材料常作为作动器用于主动控制当中。对主动控制的研究多是在对隔振系统的主动控制方法的开发和应用上[13],针对旋转叶片主动控制方面的研究较少。驼海涛等[14]用试验研究的方法,基于压电纤维复合材料(macro fiber composite,MFC)设计了一款PID(proportional integral differential)自整定控制器,降低了太阳电池阵帆板在各种外激励作用下的振动,并且加快了帆板趋于稳定的时间,使帆板的振动得以有效的控制。宋奎辉等[15]设计了一套旋转力发生器原理样机,用主动控制试验验证了其对旋翼桨毂的振动有着显著的控制效果。杨理华等[16]提出了一种不需要外界参考信号的自适应控制策略,可以应用于复杂安装环境下旋转机械的振动主动控制。张仕明等[17]提出了一种迭代-二次规划算法,进一步减小了控制信号的保守,提升了控制性能。张博等[18]将压电纤维复合材料应用于旋转叶片,用多尺度法分析了1∶2内共振条件下的一阶主共振的情形下的主动控制,分析了控制器参数对叶片振动及其稳定性的影响。利用压电纤维复合材料可以在几乎没有附加质量的条件下完成对旋转叶片的振动控制。虽然主动控制方法适合用于在非线性结构中,但是在信号传递过程中,不可避免得会产生时滞。Xu等[19]研究了考虑时间延迟的van der Pol-Duffing振荡器,研究了时间延迟对平衡点的稳定性和分岔的影响。Xu等[20]考虑了一类同时具有线性和非线性反馈的一阶时滞微分方程,从定性和定量两方面研究了对具有时滞反馈的非线性系统分岔引起的动力学问题。以上研究说明了时间延迟给系统的动力学行为带来的影响是复杂的,如何利用时间延迟带来的有利因素,也是重点研究的方向之一。

长期以来,对旋转叶片的研究大多通过研究其不同条件下的振动特性,优化结构参数设计或调整转速以降低叶片的振动,少有通过主动控制的方法来控制叶片振动的研究。故本文基于梯度环境下旋转叶片动力学模型,引入MFC传感器和作动器建立闭环受控系统。近期Lu等[21]利用MFC压电纤维复合材料,设计了自适应控制系统,用试验验证了控制效果的有效性。本文采用PD(proportional differential)控制,控制效果明显,控制过程简单。采用多尺度的方法分析了受控叶片在二阶主共振情形下稳态响应,揭示了叶片的响应随控制参数演变的规律。

1 模型描述和控制系统运动方程

本文研究的基于MFC压电纤维复合材料的旋转叶片振动控制系统,如图1所示。在叶片两侧对称地布置MFC传感器和作动器。控制器工作时,MFC传感器测量叶片位移信号并传输给计算机,经过分析运算后得到控制信号,并将控制力信号输出给MFC作动器,通过作动器的响应实现对旋转叶片的振动控制。

图1 包含MFC传感器和作动器的旋转叶片示意图Fig.1 Schematic of a rotating blade containing an MFC sensor and actuator

叶片模型如图2所示。本文采用2016年Zhang等研究中的利用Lagrange原理结合假设模态法再通过模态变换得到的叶片旋转时的动力学方程。控制过程如图3所示。在2019年Zhang等和顾伟等的研究中,立方非线性项对系统响应的影响很小,所以本文不计立方非线性项,运动微分方程为

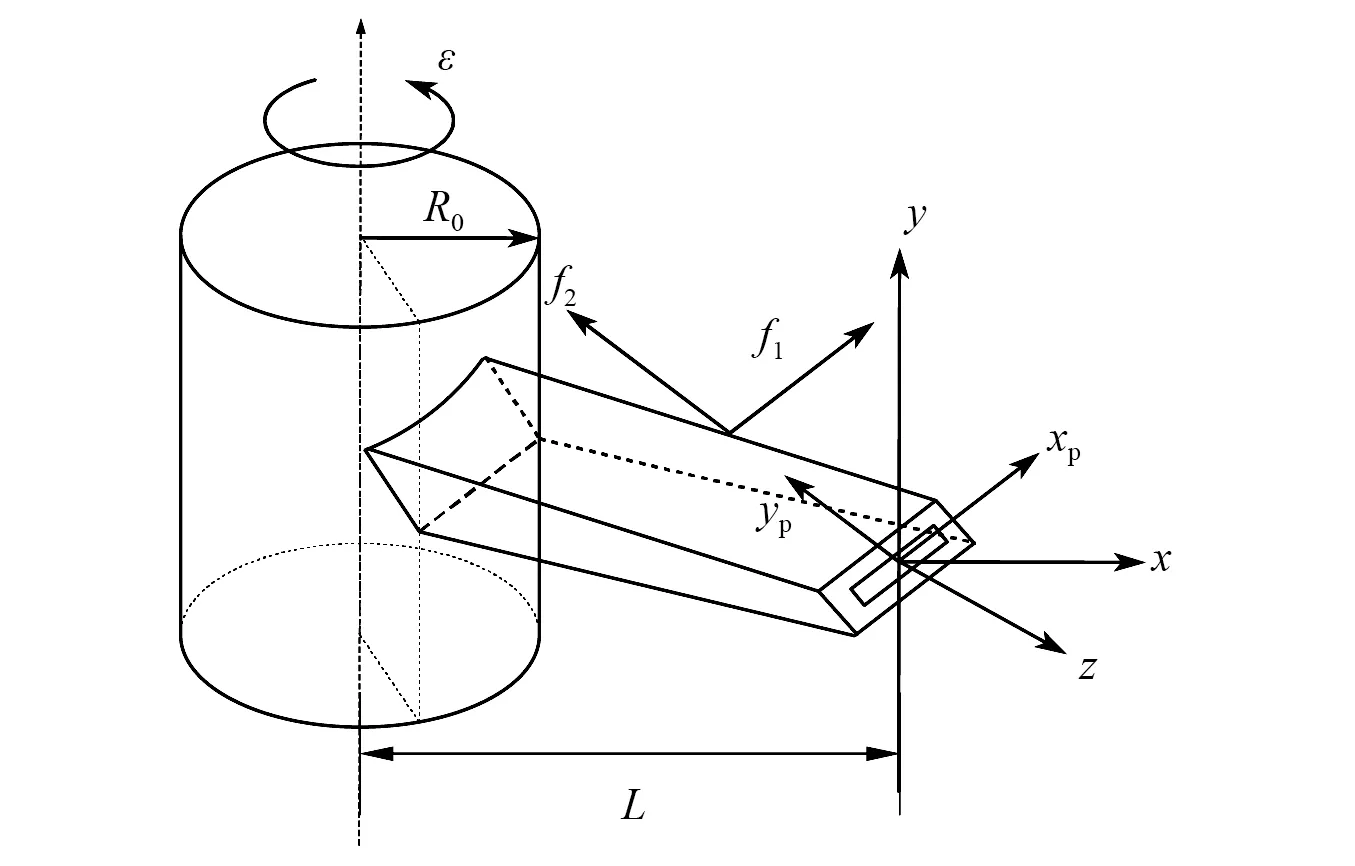
图2 模型坐标选取与受力示意图Fig.2 Schematic diagram of model coordinate selection and force

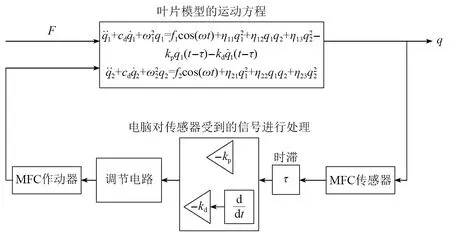
图3 控制过程方框图Fig.3 Control process block diagram

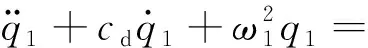
(1)

(2)

式中:q1,q2分别为弦向和翼向模态坐标;cd为无量纲阻尼系数;ω1,ω2为叶片前两阶无量纲固有频率;u(t)具体表达式为

(3)

式中:kp为位移反馈增益;kd为速度反馈增益;τ为信号采集、传输、运算、响应等环节产生的时间延迟,通常是一个小量;其他参数的意义可以参考张博等的研究。

2 多尺度法的摄动分析

对方程进行重刻度,并引入两个时间尺度

q1,2↔εq1,2,cd↔εcd,f1,2↔ε2f1,2,
kp↔εkp,kd↔εkd,T0=t,T1=εt

(4)

式中,ε为无量纲小参数。采用多尺度法,假设式(1)和式(2)的解分别为

q1(t)=q10(T0,T1)+εq11(T0,T1),
q2(t)=q20(T0,T1)+εq21(T0,T1)

(5)

后文会利用数值积分验证近似解的合理性。

则考虑延迟效应下,采集到的弦向位移信号

q1(t-τ)=q10(T0-τ,T1-ετ)+

εq11(T0-τ,T1-ετ)=

q10τ(T0,T1)+εq11τ(T0,T1)

(6)

将式(5)、式(6)代入式(1)、式(2)并对比同幂次系数

ε项

(7)

ε2项

(8)

式(7)的通解为

q10=A1(T1)eiω1T0+cc,
q20=A2(T1)eiω2T0+cc

(9)

式中:cc为前面各项的共轭复数;A1,A2为T1的复函数,写成极坐标形式

(10)

由式(6)和式(9)得

q10τ(T0,T1)=A1(T1-ετ)eiω1(T0-τ)+cc=

A1τeiω1(T0-τ)+cc

(11)

根据假设τ为小量,Taylor展开,因为

A1τ(T1)=A1(T1-ετ)=

A1(T1)-ετD1A1+o(ε2)

(12)

本文讨论1∶2内共振条件下的二阶主共振,引入解谐参数

ω2=2ω1+εσ1,ω=ω2+εσ2

(13)

将式(9)～式(13)代入式(8)得

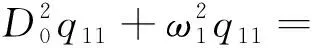
kpA1eiω1(T0-τ)-kdD0A1eiω1(T0-τ)+cc

(14)

避免久期项的出现,需满足

kpA1e-iω1τ-kdiω1A1e-iω1τ=0,

(15)

分离实部和虚部,得到受控系统自治演化方程

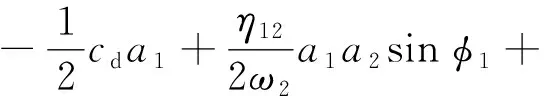
(16)

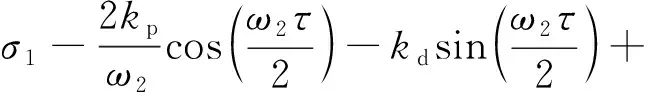
(17)

(18)

(19)

式中,φ1=σ1T1-2β1+β2,φ2=σ2T1-β2为了研究该受控系统的稳态响应,可令受控系统演化方程等号左侧为0。本文采用Mathematica研究受控系统的动力学行为。

用李雅普诺夫稳定性理论研究演化方程的稳定性。

3 受控系统响应演化规律

采用张仕明等研究中的参数,如表1所示。

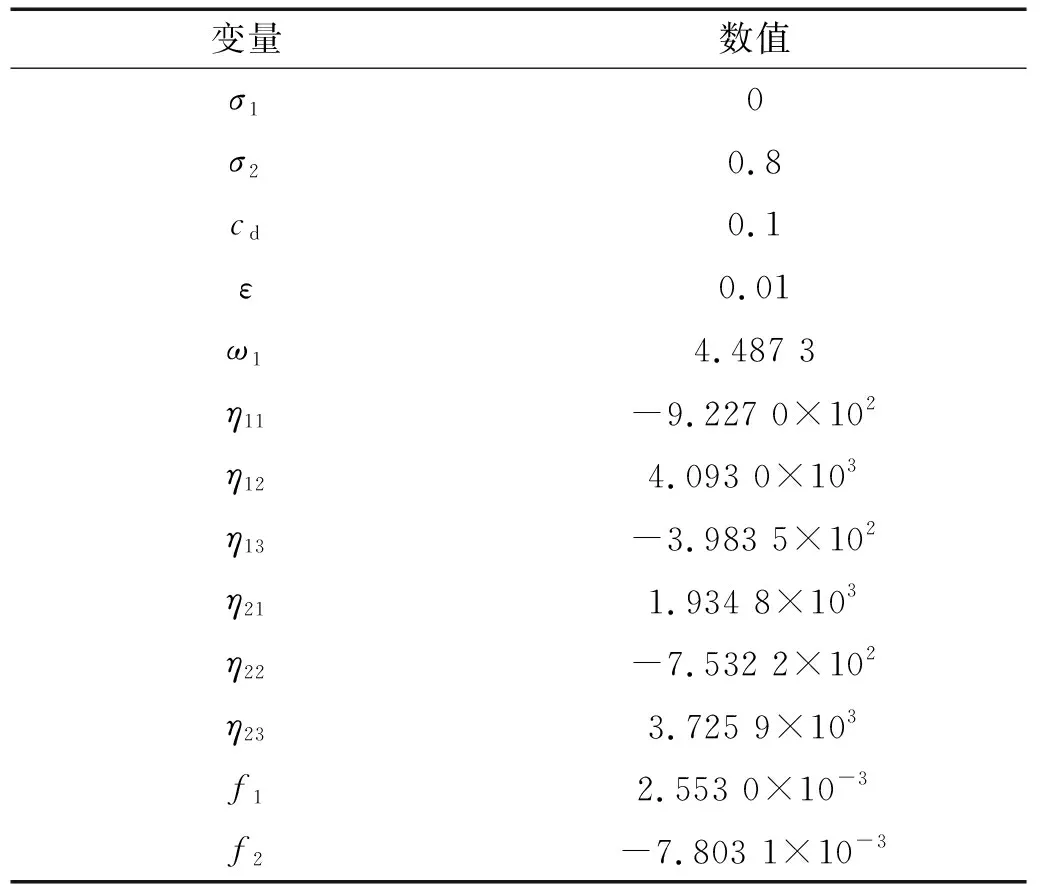
表1 算例系统计算参数Tab.1 Parameters of example toroidal drive system

与一阶主共振不同的是,二阶主共振时的解析解分为单模态解和双模态解。

为求出稳态响应时振幅的解析解,令式(16)～式(19)的左侧等于0,解出a1,a2的解析解。

单模态解:

对于式(16),a1=0显然是式(16)的一个解。故将a1=0代入式(18)和式(19),得

(20)

根据式(20)解得

(21)

进而可得到关于a2的响应方程

由式(22)可解得稳态响应的单模态解

a1=0

(23)

(24)

非线性方程通常伴随着多解,当a1≠0时,可以得到方程的双模态解。

双模态解:

根据式(16)～式(19),解得

再令式(25)左侧φ1与φ2对应的正余弦平方和等于1,可消去φ1与φ2,得到响应方程

(26)

其中,

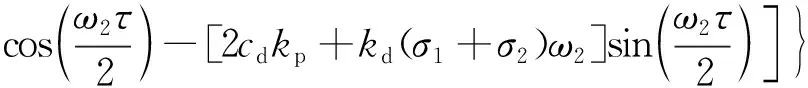
(27)

解得

(28)

(29)

当稳定在双模态解时,前两阶模态都有响应。用a1,a2稳态时,的解析解分析旋转叶片发生1∶2内共振时,受控旋转预变形叶片的稳态动力学响应,图中稳定部分用粗线画出,不稳定部分用细线画出。

如图4所示,在关于σ2=0对称的激励频率范围出现两次跳变现象,两个峰向相反的方向弯曲,这被称为双跳跃现象。从图4中可以看到,当速度增益kd增加时,能使方程达到双模态解的激励频率范围变窄,系统更容易收敛到单模态解,并且双模态解的最值也随着kd的增大而减小,这说明速度增益可以有效地抑制两阶模态的振幅,这相当于增加了系统的阻尼。

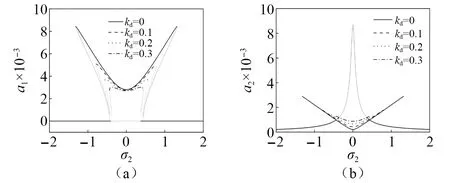
图4 不同速度增益kd下受控系统频响应曲线(τ=0)Fig.4 Frequency response curve of the controlled system for different speed gains kd(τ=0)

如图5所示,曲线不再以σ2=0为对称轴对称,说明引入位移增益相当于破坏了系统1∶2内共振的条件,峰值出现在V形曲线的最左端。随着位移增益kp增大,双模态解的最低点逐渐向右偏移。从图5中发现,在一定的频率范围增大kp反而会使振幅增大。这说明位移增益需要适当选取。此外,从图5(a)还可以看出,当σ2=0时,V形曲线都交于一点,说明此时位移增益对叶片没有控制效果。

图5 不同位移增益kp下受控系统频响应曲线(τ=0)Fig.5 Frequency response curves of controlled systems for different displacement gains kp(τ=0)

如图6所示,第一阶模态响应随kp变化的曲线朝左侧弯曲,出现多值现象,且峰值随着时间延迟τ增大而减小,曲线的峰值到0值中间出现一段不稳定区域,且随着τ增大,不稳定区间逐渐减小。但是当τ增大到0.03时,系统在一定kp范围内出现所有的解都不稳定的情况。不稳定时系统可能会是发散的,这种情况应该被避免。第二阶模态随kp变化的曲线也在一段区间内出现多值情况,并且峰值随着τ增大而减小。

图6 不同时间延迟τ下a1,a2随kp的变化曲线(kd=0)Fig.6 The curve of a1,a2 with kp for different time delay τ(kd=0)

如图7所示,当kd为在一段取值为负数的区间内,会令系统不稳定,随着时滞量增加,系统的稳定部分逐渐向右侧偏移。当取值达到稳定后,kd增大,会降低第一阶模态的响应,第二阶模态响应先减小后增大,继续增大kd,两阶模态都将稳定至单模态解。

图7 不同时间延迟τ下a1,a2随kd的变化曲线(kp=2)Fig.7 The curve of a1,a2 with kd for different time delay τ(kp=2)

如图8所示,适当选取kp的值,可以有效降低在kd变化过程中的峰值。

图8 不同位移增益kp下a1,a2随kd的变化曲线(τ=0)Fig.8 The curve of a1,a2 with kd for different displacement gains kp(τ=0)

4 时滞量对控制器稳定性的影响

图9绘制了不同时滞量下受控系统在速度-位移增益平面内的稳定区域与不稳定区域图,其中:区域A为不稳定区域;区域B为单模态解稳定但是双模态解不稳定的区域;区域C为双模态解稳定但是单模态解不稳定的区域;区域D为单模态解和双模态解都稳定的区域。 从图9中可见,随着时滞量增大,不稳定区域的边界逐渐倾斜。

图9 不同时滞量下受控系统增益稳定性区域Fig.9 Area of gain stability of the controlled system for different time delays

如图10所示,在图9(c)中稳定区域与不稳定区域的交界处取一点kd=0.216 4,kp=3.322, (在图9(c)中用黑色的点标出)绘制了稳态响应随时时滞量的变化曲线。发现在不同频率下的临界时滞相差较小。

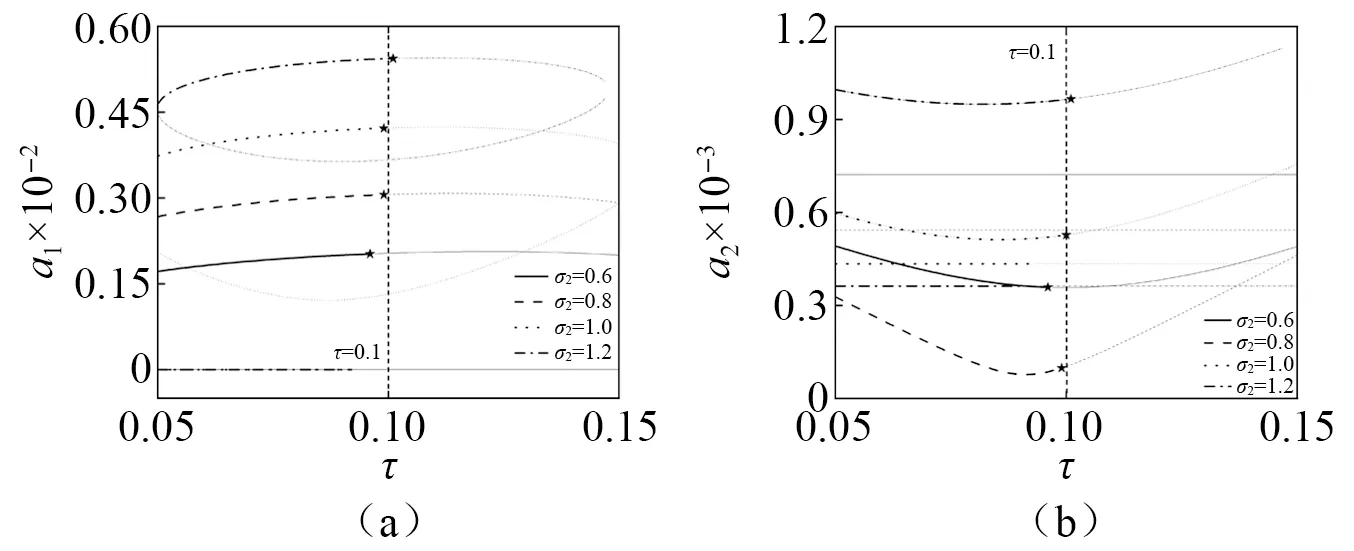
图10 稳态响应随时滞量的变化曲线(kd=0.216 4,kp=3.322)Fig.10 The curve of the steady-state response with time delay(kd=0.216 4,kp=3.322)

5 数值积分

如图11所示,为验证多尺度法的正确性,用龙格库塔法对式(1)、式(2)进行数值积分。时滞量τ接近0.1的过程中控制效果逐渐减弱;当时滞量τ达到0.1时,失去控制效果;当时滞量τ超过0.1时,将时间延长5倍,发现系统变得不再稳定,系统的振幅急剧增加。

图11 不同时滞量下受控系统响应的时间历程Fig.11 The time history of the controlled system for different time delay

如图12所示,用龙格库塔法对式(1)、式(2)进行数值积分,并把时间选取得足够长让系统进入稳态,对原系统进行正反扫频,其中:圆圈代表正向扫频时的数值积分点;方块代表反向扫频时的数值积分点;曲线代表多尺度法求出的解析解。 发现正反扫频时发生跳跃现象的跳跃点不同,在跳跃点处响应发生突变。数值积分与解析解吻合良好,验证了多尺度法的正确性。

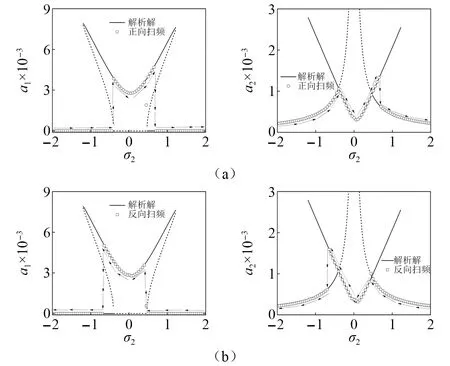
图12 正反向扫频数值积分结果与解析解的对比(kd=0.1, kp=0.2, τ=0.05, cd=0.05)Fig.12 Comparison between the integral result of forward and reverse sweep frequency values and the analytical solution (kd=0.1, kp=0.2, τ=0.05, cd=0.05)

6 结 论

本文研究了旋转叶片的闭环控制系统,采用多尺度法得到了1∶2内共振的二阶主共振时受控系统的自治演化方程,通过演化方程得到了系统稳态响应的一阶近似振幅的解析解,用解析解进行后续的参数分析,分析了系统的动力学行为,研究了时滞对系统稳定性的影响。通过数值验证,一阶近似振幅与原系统响应振幅吻合较好,也证明了多尺度法的准确性。得到如下结论:

(1)1∶2内共振的二阶主共振的演化方程具有两对平衡点,响应曲线会出现多值现象。

(2)位移增益使频响曲线的峰值偏移,因为位移增益可以近似看作是改变了ω2的值,这相当于破坏了系统1∶2内共振的条件。

(3)在接近临界时滞的过程中控制效果逐渐减弱,超过临界时滞后系统发散。

(4)数值积分验证了多尺度法的正确性,正反向扫频的跳跃点不同。

(5)展望:叶片在特定转速下,前两阶固有频率会出现公度关系,此时前两阶模态会存在能量交换,形成内共振。本文针对1∶2情形的内共振,分析了考虑时滞效应的PD反馈控制对叶片控制效果,验证其可在几乎不影响叶片质量的前提下对叶片的振动进行控制,可以有效地避免叶片振动带来的危害,具有工程应用价值。日后将会对1∶3内共振,谐波共振等不同共振情况的主动控制进行研究。