Periodic electron oscillation in coupled two-dimensional lattices

Yan-Yan Lu(陆艳艳), Chao Wang(王超), Jin-Yi Jiang(将金益), Jie Liu(刘洁), and Jian-Xin Zhong(钟建新)

Hunan Key Laboratory of Micro-Nano Energy Materials and Devices,School of Physics and Optoelectronics,Xiangtan University,Hunan 411105,China

Keywords: quantum diffusion,periodic oscillation,coupled systems,disorder,Anderson localization

1.Introduction

The Bloch oscillation is a quantum phenomenon that occurs in periodic lattices due to Bragg reflection when electrons are subjected to a constant electric field,which differs significantly from the behavior of accelerated motion in classical physics.[1,2]It is further proved[3,4]that a constant electronic field transforms the continuous electronic band spectrum of a periodic lattice into a series of equidistant energy levels separated by the energy spacing ∆E=eFaand superposition of the localized Wannie–Stark eigen-states results in periodic oscillation of electrons with temporal periodicityTB=h/(eFa)and spatial widthLB=WB/(eF),whereWB,F,a,eandhare the electronic bandwidth, the applied electronic field, the lattice spacing,the electron charge,and the Planck constant,respectively.It was very difficult to realize the Bloch oscillation in crystals due to the bearing capacity of electronic field in real materials and the lose of electron coherence caused by impurities,defects,and atomic thermal vibrations.Two approaches have been employed to observe the Bloch quantum oscillation in periodic systems, focusing on either increasing the lattice spacing or increasing the coherence time.After 60 years of its prediction,Bloch oscillation was first observed successfully in semiconductor superlattices by significantly enlarged the superlattice spacing in the order of thousands of times larger than the atomic scale.[5–7]In recent years, systems of cold atoms in optical potential lattices have been widely used to simulate and study quantum behaviors of electrons in solids because of longer decoherence time for atoms and wide range of tunability for lattice geometry and lattice spacing as well as atom–potential and atom–atom interactions.The Bloch oscillation of cold atoms has been realized in various experimental setups.[8–14]The Bloch oscillation of quantum particles in periodic systems in nature is a phenomenon of wave scattering and thus has also been observed in optical[15–19]and phonon systems[20]in recent years.Nevertheless, it has been a great challenge to realize periodic electron oscillation in materials at atomic scale.

We recently found that quantum diffusion of electrons(time evolution of electron wavepackets) in the coupled two identical one-dimensional (1D) lattices of mirror symmetry exhibits a well-defined periodic oscillation with a frequency determined by the interchain hopping strength and undergoes a damped periodic oscillation when random perturbation of site potentials exists.[21]In this paper, using coupled square lattices as a model system,we expand upon the theory of periodic electron oscillation for coupled 1D lattices to coupled 2D crystals of multiple atomic layers with mirror symmetry in the framework of tight-binding Hamiltonian.We show that the wavepacket of an electron initially located on one atomic layer in the coupled 2D lattices exhibits the same type of periodic oscillation or damped periodic oscillation (with disordered potentials) in both transverse and longitudinal directions with the frequency determined by the interlayer hopping strength.With the research advances in 2D materials in recent years,few-layer graphene can be routinely obtained experimentally.[22–28]We numerically study quantum diffusion in the AA-stacked bilayer and tri-layer graphene films with mirror symmetry to verify the universality of the periodic oscillation independent of lattice geometry and to provide theoretical guidance for its possible experimental realization.

2.Theory

On the basis of the periodic oscillation of quantum diffusion in the coupled two identical 1D lattices of mirror symmetry,[21]we develop a general theory for periodic electron oscillation in the coupled multiple layers of identical 2D lattices of mirror symmetry.The system of coupled square lattices ofmlayers shown in Fig.1 with lattice spacingaand lattice sitesNfor each layer is used to present the theory.The Hamiltonian of the systemHhas the following tight-binding form:

whereHαis the sub-Hamiltonian for each layer andHα,βrepresents the coupling between different layers.In the framework of tight-bonding scheme with nearest-neighbor hopping,HαandHα,βare given by

Fig.1.Schematic illustration of the system for coupled 2D atomic layers of square lattice with mirror symmetry.Parameters εi,v,and u correspond to onsite potential, nearest-neighboring intralayer hoping and interlayer hoping,respectively.

The eigen-states of the coupled lattices are given by the Schr¨odinger equationH|ψ〉=E|ψ〉,whereEand|ψ〉are the eigenenergy and eigenvector, respectively, which can be derived from the iso-spectrumel(l=1,2,...,N)and their corresponding eigenvector〉for themidentical layers given by Schr¨odinger equationswith

EigenenergyEand eigenvector|ψ〉 of the coupled system ofmidentical 2D layers can be obtained from Eq.(7).

For the system of coupled three 2D lattices,eigenenergyEk(k= 1,2,...,3N) and eigenvector|ψk〉 are given by the three sets of values,andand their corresponding eigenvectors from Eq.(7)

The time evolution of an electron wave packet[29,30]in the coupled layers is described in general by

where coefficientCkis determined by the initial condition of the wave packet.We note thattin Eq.(10)is rescaled by the Planck constant ħ.Assuming the electron is initially located at siten0on layer 1, one hasCk=〈ψk/1,n0〉.Substituting Eqs.(8) and (9) into Eq.(10), we can derive the analytical form ofΨ(t)for the coupled two layers and three layers.

For the system of coupled two 2D lattices,

ProjectingΨ(t) to local orbitals of lattice sites, we have the wavefunction at sitenon different layers)(t)with

The probability of finding electron on different layers is thus given by

where ∆rn=rn −rn0is the planar position difference.Substitution of Eq.(13)into Eq.(15)leads to

For the system of coupled three layers of 2D square lattices with electron initially located at a site on the top layer,we have

From Eq.(9) and projectingΨ(t) to local orbitals of lattice sites, we have the wavefunctionα)(t)at sitenon different layers

The probability of finding electron on different layers is thus given by

The spreading widths on different layers follow

whereds(t) is the spreading width of the wavepacket on the isolated single layer without coupling.The form of periodic oscillation depends on the initial position of the electron.When the electron is initially located at a site on the middle layer,we have

and

For large time,sinceds(t)≈d(t)due tods(t)≫a,Eqs.(16),(20),and(22)indicate that the fluctuation of spreading width on different layers is given by(t)=(t)/d2(t)=Pα(t).Therefore, the probability of finding electron and the spreading width on each layer exhibit a well-defined periodic oscillation with frequencies determined by the interlayer hopping strength.For the system of coupled two layers with electron initially located on one layer,the oscillation frequency isf0=u/π.For the coupled system of three layers with electron initially located on the middle layer, electron appears on different layers with an oscillation frequency.For the coupled system of three layers with electron initially located on the outer layer, the occurrence oscillation frequencies for middle layer and outer layers areand, respectively.From the above theoretical analysis,one can see that the existence of the periodic oscillation is a result of energy level splitting of the iso-spectrum for the identical 2D crystals under interlayer coupling,independent of the system size and boundary condition.Therefore, the periodic oscillation persistently exists before and after the wavepacket reaches the boundary.Equations (8a) and (9a) indicate that the level of energy splitting is of the order of interlayer hopping strengthu.Thus,one expects that the periodic oscillation exists in the coupled disordered 2D crystals if the strength of disorder is smaller thanu.This is indeed the case in the coupled identical 1D systems with Anderson disorder of strengthW, where a damped periodic oscillation occurs with a decay time inversely proportional to the square ofWand a slight frequency change proportional to the square ofW.[21]It is interesting to examine if the behavior of damped periodic oscillation still holds in the coupled 2D lattices.

3.Numerical results

We use the coupled two/three identical layers of square lattice to numerically illustrate the periodic electron oscillation.The system size ofN=51×51×2 and open boundary condition are used in the calculations.The method of direct diagonalization of Hamiltonian is employed to directly solve the static and time-dependent Schr¨odinger equations and calculate the wavefunctions,probabilities of finding electron,spreading widths of electronic wavepackets.The initial location of the electron is at the center of layer 1.

Figure 2 illustrates the behavior of quantum diffusion in the coupled bilayers withεi=0,v=1,andu=1.Figure 2(a)shows that the spreading width of wavepacketd(t) increases linearly with time and stops increasing after the wavepacket reaches the boundary att ≈10.5 as shown by the probability of finding electronPb(t) on boundary sites in the upper inset of Fig.2(a).Further analysis of the numerical results confirms thatPα(t) (α=1,2) and the fluctuation part ofdα(t)exhibit the periodic oscillation at any time (before or after the wavepacket reaches the boundary) with the frequency off0=u/πgiven by Eqs.(14)and(16).As examples,behaviors of periodic oscillation ofPα(t)anddα(t)are illustrated in the lower insects in Fig.2(a) for time intervals 0≤t ≤10.5 and 75≤t ≤85 corresponding to the cases for the wavepacket before reaching and after reaching the boundary, respectively.Examples of onsite distributions of probabilityP(1)n(t) andP(2)n(t) on different layers at the time after different successive periods of oscillation are shown in Fig.2(b).One can clearly see that the wavepacket occurs only on the upper layer att=3.14 or the bottom layer att=4.71 and repeats the same behavior att=590.62 ort=592.19,spreading out on two layers alternatively with the periodicity given byf0=u/π.

Disorder may exist in the system of coupled layers.We use the Anderson-type model of disorder.[21,31–34]to examine the stability of the periodic oscillation against disorder by adding a random value in the interval [−W,W] to all onsite energies of the system.Through analysis ofPα(t) anddα(t) on the system of disordered coupled bilayers, we find thatPα(t)and ¯d2α(t)exhibit the same damped periodic oscillation as found in coupled 1D systems described by

where the decay timet0followst0∼W−2and the frequency parameterfhas a slight increase asWincreases described by∆f=f −f0∼W2.

Fig.2.Time evolution of wave packet in the coupled bilayer square lattices with N =51×51×2, εi =0, v=1, and u=1.(a) Spreading width of the wave packet d(t)in the coupled system and associated spreading width dα(t) and probability Pα(t) on layer 1 (blue line) and layer 2 (red line) in two typical time intervals as marked by arrows.The upper inset shows the total probability of finding electron Pb(t)at boundary sites and the time of the wave packet reaching the boundary is marked by dashed line.(b) Onsite distributions of wave packet )(t) on layer 1 and 2) (t) on layer 2 at the time after 1(t =3.14), 1.5(t =4.71)periods of oscillation and 188(t=590.62),188.5(t=592.19)periods of oscillation.

Figure 3 illustrates quantum diffusion in disordered bilayers of sizeN= 51×51×2 with 20 different configurations of disorder,wherev=1,u=1,andεi ∈[−W,W].Figure 3(a)shows the behavior ofd(t)withW=1.As expected,d(t) stops increase before reaching the boundary as shown in Fig.3(a) due to the localization of eigenstates in the 2D disordered systems.The oscillation lengthdα(t) and probabilityPα(t) still show periodic oscillation, but their amplitudes decay with time.As examples, the periodic oscillations ofdα(t) and probabilityPα(t) are shown in the insets of Fig.3(a) during time intervals 0≤t ≤25.We focus on the analysis ofP1(t) andd1(t) due toP1(t)+P2(t)=1 and(t)+(t)=d2(t).Figure 3(b) shows the FFT frequency spectra ofP1(t)during time intervals 0≤t ≤500 for different values ofW.From Fig.3(b),one can see that the spectrum has only one frequency peak under smallWin all cases, locating at almost the same position forW=0.Under large disorder,the frequency distribution widens significantly, indicating the absence of periodic oscillation of single frequency.ProbabilityP1(t)and spreading width(t)for different values ofWand their fit to Eq.(23)are shown in Figs.3(c)and 3(d),in which parametert0is from the linear fit of the plot of ln(2P1−1)againsttas shown in Fig.3(e), whereP1is the peak value ofP1(t).Parameterfis from fitting numerical results ofP1(t)and(t)to Eq.(23).Values oft0andfversusWin Fig.3(f)clearly show that the data can be well fitted byt0∼W−2and∆f=f −f0∼W2.

Fig.3.Time evolution of wave packet in the coupled disordered 2D square lattices with N=51×51×2,v=1,u=1,εi ∈[−W,W]and different degrees of disorder W.(a)Spreading width of wave packet d(t)with W =1 and associated spreading width dα(t)and probability Pα(t)on layer 1(blue line)and layer 2(red line)in the time intervals as marked by arrow.(b)FFT frequency spectrum of probability P1(t)as a function of W.(c)and(d)P1(t)and(t)=(t)/d2(t)for W =0.5,0.7,0.9(open circles)and corresponding fitting results(lines)with t0=33.3,16.6,9.9 and f =1.006,1.011,1.016, respectively.(e)ln(2P1−1)versus t for W=0.3,0.4,0.5,0.6,0.7,0.9(symbols)and corresponding linear fitting results (lines) with t0 =94.7,52.3,33.3,22.8,16.6,9.9, respectively, where P1 is the peak value of P1(t).(f) Values of t0 and f versus W(symbols)and corresponding fitting results(lines)to t0 ∼W−2 and ∆f = f −f0∼W2 (inset).

Fig.4.Time evolution of wave packet in the coupled disordered 2D square lattices of three layers with N =51×51×3, v=1, u=1, εi ∈[−W,W]and different degrees of disorder W.(a)and(b)P2(t)and(t)=(t)/d2(t)for W =0.3,0.6,0.9(open circles)and corresponding fitting results(lines)with t0=65.28,15.83,6.98 and f =1.41774,1.42621,1.43728,respectively.(c)FFT frequency spectrum of probability P2(t)as a function of W.(d)Values of t0 and f versus W (symbols)and corresponding fitting results(lines)to t0 ∼W−2 and ∆f = f −f0 ∼W2.

The perfect fit of the damped periodic oscillation to Eq.(24)can be seen in Figs.4(a) and 4(b).The relationship between the values oft0andWis described byt0∼W−2shown in Fig.4(d).The slight change of frequency can be well fitted by∆f=f −f0∼W2as shown in inset of Fig.4(d).

4.Coupled system of graphene layers

We apply the theory to AA-stacked bilayer and tri-layer graphene films with mirror symmetry for verifying the universality of periodic oscillation as well as for the possible experimental realization of periodic electron oscillation.The system size used isN=7688 withx=31×2a,y=31×a,z=d,whereais lattice spacing equal to 0.142 nm,anddis the distance between the layers equal to 0.335 nm,nearest-neighbor intralayer hopingv=−2.7 eV.[35,36]In the case of disordered bilayer graphene,numerical results are from the average of 20 different disordered configurations for reliable results.

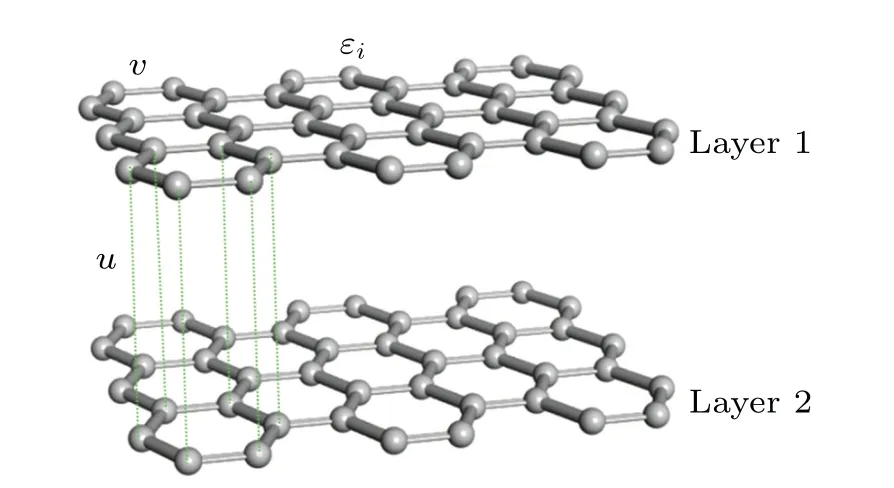
Fig.5.Schematic illustration of coupled bilayer graphene layers with mirror symmetry(AA stacking).Parameters εi,v,and u correspond to onsite potential, nearest-neighboring intralayer hoping, and interlayer hoping,respectively.

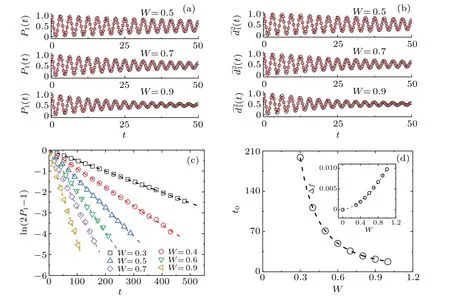
Fig.6.Time evolution of wave packet in the coupled bilayer graphene with N =3844×2, v=2.7, u=1, εi ∈[−W,W] and different degrees of disorder W.(a)and(b)P1(t)and(t)for W =0.5, 0.7, 0.9(open circles)and corresponding fitting results(lines)with t0 =71.115, 36.112, 21.858 and f =1.00288, 1.00531, 1.00823, respectively.(c) The plot of the values of ln(2P1−1) versus t for W =0.3, 0.4, 0.5, 0.6, 0.7, 0.9 (symbols) and corresponding linear fitting results (lines) with t0 =198.78, 111.3, 71.115, 49.328, 36.111, 21.858, respectively, and P1 is the peak value of P1(t).(d)Values of t0 and f versus W (symbols)and corresponding fitting results(lines)to t0 ∼W−2 and ∆f = f −f0 ∼W2 (inset).

Electron in bilayer graphene exhibits the same periodic oscillation with the frequency given byf0=u/πand the same behavior of damped periodic oscillation described in Eq.(23).Figures 6(a)and 6(b)illustrate the damped periodic oscillations ofP1(t)and(t),respectively.From the amplitudes of the damped oscillation,we obtain the characteristic decay timet0through fitting as shown in Fig.6(c).By substitutingt0into Eq.(23) and fitting the data ofP1(t) and(t) to Eq.(23), we obtain the frequencyfof the damped periodic oscillation.Excellent fits toP1(t)and(t)can be seen from Figs.6(a)and 6(b).Changes oft0andfwithWare shown in Fig.6(d).The relationship between the values oft0andWis described byt0∼W−2.Inset of Fig.6(d)shows that ∆f=f −f0∼W2.

Fig.7.Time evolution of wave packet in the coupled tri-layer graphene with N=3844×3,v=2.7,u=1,εi∈[−W,W]and different degrees of disorder W.(a) FFT frequency spectrum of probability P2(t) as a function of W.(b) and (c) P2(t) and (t) for W =0.3, 0.6, 0.9 (open circles)and corresponding fitting results(lines)with t0=128.88,32.096,14.16 and f =1.41561,1.4193,1.42443,respectively.(d)Values of t0 and f versus W (symbols)and corresponding fitting results(lines)to t0 ∼W−2 and ∆f = f −f0∼W2.

For the tri-layer graphene,electron displays the same periodic oscillation behavior as in bilayer graphene but with different frequenciesgiven by Eqs.(19)–(22).When disorder exists, the damped periodic oscillation is described by Eq.(24).Figure 7(a)illustrates the frequency distribution of damped oscillations ofP2(t) asWincreases,which shows a distinctive peak around the intrinsic frequency under weak disorderW

5.Discussion and conclusions

In summary, we have developed a general theory for the periodic oscillation of electronic wavepacket spreading in coupled systems of 2D periodic crystals with mirror symmetry in the framework of tight-binding Hamiltonian without disorder or with disordered potentials.Using coupled bilayer and tri-layer 2D square lattices, we analytically and numerically showed that time evolution of an electronic wavepacket initially distributed on one atomic layer exhibits a periodic oscillation in both vertical direction and horizontal direction with frequencies determined by the interlayer hopping strength and the number of atomic layers.The underlying mechanism for the periodic oscillation is the equal-level splitting of every level of the iso-spectrum of the identical 2D lattices,irrelevant to the system size and boundary condition.We further examined the stability of the periodic oscillation in coupled 2D crystals with disordered site potentials and numerically show that the wavepacket undergoes the same behavior of damped periodic oscillation as found in the coupled 1D disordered systems.Finally,we applied the theory to the AA-stacked bilayer and tri-layer graphene of honeycomb lattice with mirror symmetry and found the same behaviors of periodic oscillation and damped periodic oscillation, which provide a theoretical guidance for the observation of the periodic oscillation in experiments.The periodic oscillation here for the coupled systems of 2D crystals with mirror symmetry has the same forms found in the coupled 1D systems with mirror symmetry.[21]This universal periodic oscillation can be understood from the physical perspective of the mirror symmetry of the Hamiltonian and the effect of finite size quantum confinement.Under transverse mirror symmetry, the electron wavefunction in the coupled identical 2D systems(or 1D systems)is given by the product of the 2D system (or 1D system) and the wavefunction of the transverse chain of finite size composed ofmatoms (m ≥2).[29]The confinement of electron under finite size along transverse direction results in the periodic oscillation of electron within the distance ofmatoms,which in turn leads to the periodic oscillation along the longitudinal direction within the spreading width of the wavepacket determined by the 2D (or 1D) system.Because the periodic oscillation is caused by the transverse chain ofmatoms of mirror symmetry,its frequency is determined solely by the interlayer(or interchain)coupling strength,irrelevant to the dimensionality and the type of onsite potentials in the 2D(or 1D)systems.It is intriguing that the disorder results in the same behavior of damped periodic oscillation both in coupled 1D systems and 2D crystals with the universal scaling behaviorst0∼W−2and∆f=f −f0∼W2, which might come from the similarity of localization of wavefunctions in 1D and 2D disordered electron systems.

The periodic electron oscillation in coupled 2D crystals shares some common features with Bloch oscillation driven by electronic field.In both cases, the electron exhibits periodic oscillation at atomic scale with ultra-high frequencies.For the coupling-induced oscillation, the electron oscillates periodically between different layers and its width increases with time when the wavepacket does not reach the system boundary and is determined by the system lateral size for longer time.The spatial width of the Bloch oscillation is finite determined by the electric field.The periodicity of the Bloch oscillation is given byTB=h/(eFa).Because the bearing capacity of electric filed in materials is in the range ofF ∼105–107V/m,one hasTB∼10−10–10−12s,which is larger than the electron decoherence time in materials.Considering the rescaling factor Planck constant ħ, one has the realistic periodicity for the coupled bilayer system given byTC=h/(2u).Because the interlayer coupling is in the rage of 0.01 eV to 1 eV,we haveTC∼10−13–10−15s,which is much smaller than the electron decoherence time in crystals.The coupling induced periodic oscillation has unique advantages over Bloch oscillation, including no need of applying electric field, faster oscillation with the periodicity much shorter than the electron decoherence time, and tunability by adjusting the interlayer coupling strength.Our model for the coupled 2D atomic layers paves the way for future observation of periodic electron oscillation in material systems at the atomic scale.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant No.11874316),the National Basic Research Program of China(Grant No.2015CB921103),and the International Visiting Faculty Program of Hunan Provincial Government,China.