Transport properties of CrP

Xuebo Zhou(周学博), Ping Zheng(郑萍), Wei Wu(吴伟),†,Yu Sui(隋郁), and Jianlin Luo(雒建林),4,5,§

1School of Physics,Harbin Institute of Technology,Harbin 150001,China

2Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3Laboratory for Space Environment and Physical Sciences,Harbin Institute of Technology,Harbin 150001,China

4School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

5Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: CrP,thermal transport,Wiedemann–Franz law

1.Introduction

The Wiedemann–Franz (WF) law describes the relationship between the electron thermal conductivity (κel) and the electrical conductivity (σ) of metals.In 1927, Sommerfeld used Fermi Dirac statistics and quantum mechanics to derive the theoretical relationship of the WF law[1,2]

whereeis the charge of electron,Tis the absolute temperature,kBis Boltzmann constant, andL0= 2.44×10−8W·Ω·K−2is Sommerfeld’s value.The WF law is widely regarded as a robust property of metals and one of the basic properties of a Fermi liquid, having been verified in numerous metals.Most of the charge transport behavior in conventional metals can be described by the free-electron gas model.That is,electrons are thought to travel freely until they collide with phonons or impurities.These scatters are usually elastic scatters that relax both the momentum and the energy flow.Electrical transport is related to momentum relaxation of electrons, and thermal transport is related to energy relaxation of electrons.Therefore,the blocking effect of scattering on electrical and thermal transport is similar in this case.In other words, the electron thermal conductivity and electrical conductivity of conventional metals usually obey the WF law.

Pressure-induced superconductivity has been found in CrAs, and magnetic order is suppressed with the appearance of superconductivity when a pressure of 7 kbar is applied.[3,4]The lattice structures of CrP and CrAs are the same, and the paramagnetic band structures of the two compounds are similar.[5]Both of them have non-trivial band crossing points at theYpoint, and the atomic radius of the P atom is smaller than that of the As atom,which is equivalent to chemical pressurization of CrAs.Therefore, it is necessary to study the physical properties of CrP.CrP crystalizes in the space groupPnma.In simple 3d transition-metal phosphides, there are three crystal structures, namely hexagonal NiAs-type structure, orthorhombic MnP-type structure, and orthorhombic NiP-type structure.[6]The distortion of the structure is related to the filling of electrons in the d shell: TiP and VP are the NiAs-type structure type; CrP,MnP,FeP,and CoP are the orthorhombic MnP-type structure;NiP is the orthorhombic NiPtype structure.[7,8]Schematic diagram of the transition from NiAs-type to MnP-type structure is given in Fig.1(a).CrP is a Pauli paramagnetic compound.The electron band structure of CrP was calculated at room temperature, as shown in Fig.1(b).Interestingly,there is a band crossing at theYpoint of the Brillouin zone of CrP, which is four-fold degenerate and protected by the nonsymmorphic symmetry of the space group.[5,9]CrP has a linear dispersion relationship in theY–Γdirection and a parabolic dispersion relationship in theY–Sdirection.An small Fermi pocket is formed at theYpoint,due to the crossing of∼47 meV lower than the Fermi level.[5,9]CrP is a good metal because of other multiple large Fermi surface sheets.The semi-Dirac-like energy-momentum dispersion relation nearYwill make CrP a topological semimetal in the absence of other multiple large Fermi surface sheets.[5,9]

Fig.1.(a)Schematic diagram of the transition from NiAs-type to MnP-type structure.(b)The calculation results of electron band structure and the density of states(DOS)of CrP.[10]

In this study,we carried out the heat capacity,the electrical and thermal transport measurements on CrP.By extracting the electron thermal conductivity, the thermal and electrical transport properties of CrP were compared.The normalized Lorentz number remains nearly 1 above about 160 K,but begins to decrease below 160 K due to the difference in momentum and energy relaxation time in electron–phonon inelastic scattering.The normalized Lorentz number starts to recover below 25.6 K,which comes from the fact that electron–defect scattering as elastic scattering replaces electron–phonon scattering predominates at low temperature.

2.Experimental details

CrP single crystals are grown using the Sn flux method.Polycrystal of CrP and cosolvent Sn were packed into a quartz tube sealed in vacuum.The feedstock was heated to 1150◦C and kept for two days.It took two weeks to slowly cool to 700◦C.Single crystals were obtained by centrifugation at 700◦C.A resistance heater was used to generate a heat currentj=P/Sin the plane, wherePandSare the heater power and the cross-sectional area of the sample,respectively.The voltage ∆Vwas measured by a Keithley 2182A nanovoltmeter.The temperature gradients ∆T/lwere measured with E-type thermocouples, wherelis the distance between the thermal contacts.The thermal conductivity was measured byκxx=jl/∆T.The thermal and electrical transport measurements were all performed in a 9-T Quantum Design physical property measurement system.

3.Result and discussion

Figure 2(a) shows the temperature (T) dependence of electrical resistivity (ρ) in CrP at zero magnetic field.The resistivity behavior is similar to that in the literature.[9]Figure 2(b) shows the temperature dependence of magnetic susceptibility magnetic susceptibilityχof CrP.No evidence of long-range magnetic order was found in the temperature range from 2 K to 800 K.When the temperature decreases from 800 K to 160 K,the magnetic susceptibility slowly decreases until it is lower than 160 K, the magnetic susceptibility increases.However,the overall change of magnetic susceptibility is small and there is no magnitude change.

Figures 2(c) and 2(d) show the temperature dependence of specific heatCp(T).Above 10 K,Cp(T)is dominated by the phonon contribution.Below 10 K,Cp(T)can be fitted with the standardCp(T)/T=γ+βT2expression.[11,12]A fit(red line)to the data using this expression is shown in Fig.2(c).The termγTis the electronic specific heat,and the termβT3is the phonon specific heat.The phonon specific heat conforms to the Debye model,and Debye temperature is usually equivalent to room temperature,so theβT3form of phonon specific heat is only valid at low temperatures.The electronic specific heat follows Fermi statistics.Noticeably, the thermal disturbance is much smaller than the Fermi energy at room temperature,so theγTform can be extended to the 2–300 K temperature region to obtain the electronic specific heat.The phonon specific heat is obtained by subtracting the electron specific heat from the total specific heat data.[12]The total specific heat,the specific heat of phonon(Cph),and electron(Cel)are shown in Fig.2(d).In the high-temperature range,phonon specific heat is dominant, and the effect of electron specific heat is gradually obvious with the decrease of temperature.

To address the interactions and accompanied scattering mechanism in CrP in more detail, we measured the thermal transport property.Figure 2(e)shows the temperature(T)dependence of thermal conductivity (κ).With the decrease of temperature, the thermal conductivity firstly increases until it reaches the maximum value around 24 K,and then decreases rapidly.Since the WF law generally holds at 300 K, we assume that the WF law is also obeyed at 300 K in CrP.[12]Thus,at 300 K, we can use the resistivity and the WF law to get the thermal conductivity of the electronκel(300 K).Then the phonon thermal conductivity at 300 K can also be obtained byκph(300 K)=κ(300 K)−κel(300 K).According to the relation between phonon thermal conductivity and phonon specific heat,κph(300 K)=vlCph(300 K),the coeffciientvlcan be obtained,wherevis the sound velocity andlthe phonon mean free path.By extending it to the whole temperature region(the free pathlactually increases at low temperatures), the phonon thermal conductivity can be obtained,κph=vlCph.The electron thermal conductivity is obtained by subtracting the phonon thermal conductivity from the total thermal conductivity data.[12]We have isolated phonon thermal conductivity(κph)and electron thermal conductivity(κel)from the total thermal conductivity.At 300 K, the phonon thermal conductivity is of the same order as the electron thermal conductivity,and the electron thermal conductivity gradually dominates as the temperature decreases.Figure 2(f)shows temperaturedependent normalized Lorenz numberL/L0=κel/(L0σT),whereL0is Sommerfeld’s value.The electrical and thermal transport operation of CrP is in accordance with the WF law at high temperature.Below∼160 K,L/L0starts to decline rapidly.At 25.6 K,the minimum value ofL/L0is 0.39.Below 25.6 K,it begins to show signs of recovery.

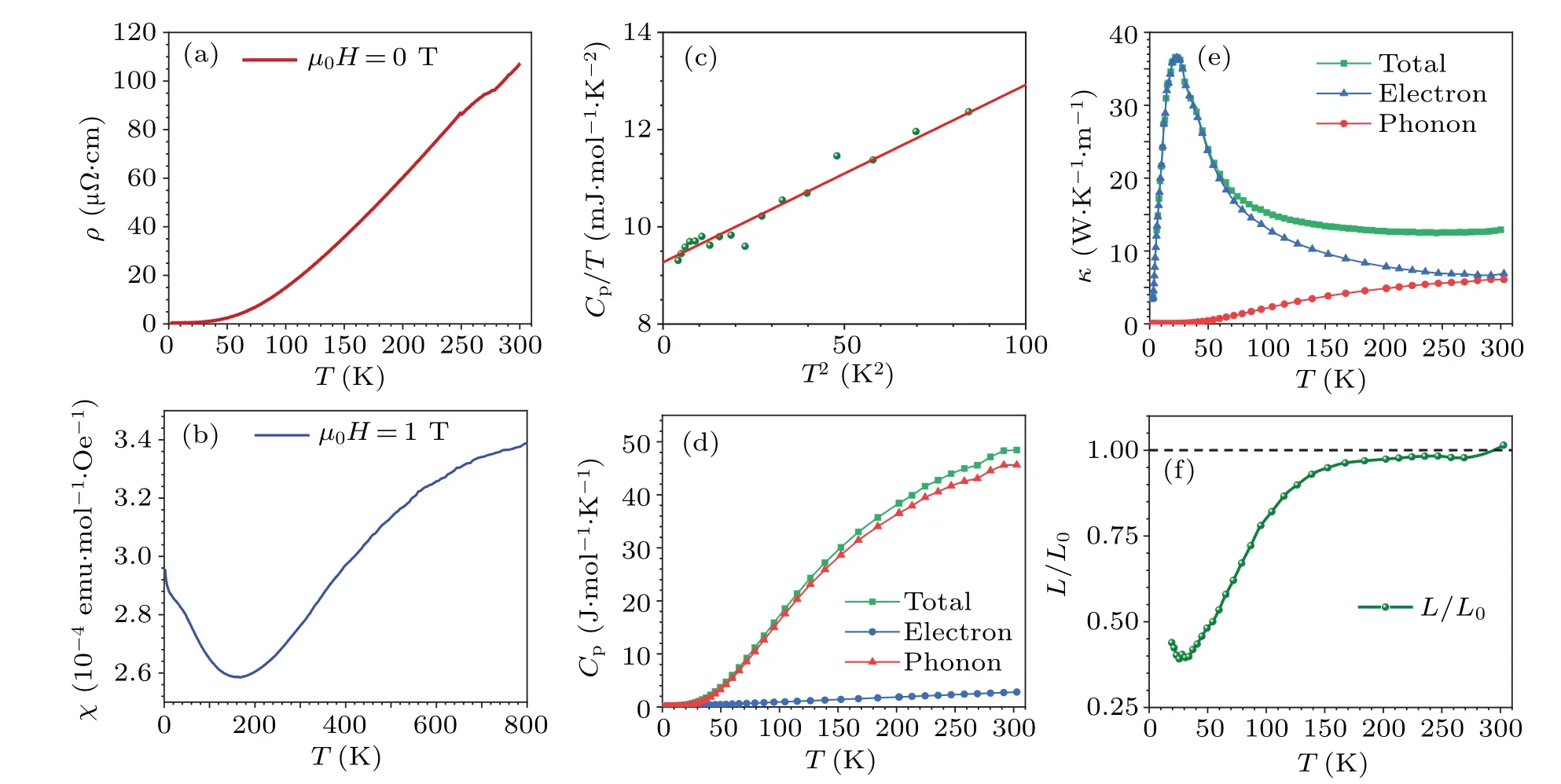
Fig.2.(a)Temperature dependence of resistivity ρ of CrP.(b)Temperature dependence of magnetic susceptibility χ of CrP.(c)Temperature dependence of the specific heat Cp(T)of CrP.The solid red line shows a fit to the data using Cp(T)/T =γ+βT2.(d)Measured temperature dependent total heat capacity, Cp (total), separated phononic part, Cph, and electronic part, Cel.(e) Temperature-dependent measured total thermal conductivity,κ (total),calculated phononic part κph (phonon)from heat capacity and the subtracted electronic part κel (electron)from the measured data.(f)Temperature-dependent normalized Lorenz number,L/L0,where L0 is Sommerfeld’s value.

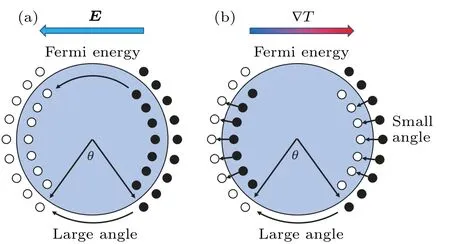
Fig.3.(a) Schematic representation of electron scattering in an electric field.The electrons close to the Fermi surface are driven by the external electrical field.The filled small spheres are occupied electron states and the open small spheres are unoccupied electron states.The electrons can only return to equilibrium through large-angle scatterings(horizontal processes).(b) Schematic representation of electron scattering under a temperature gradient.The electrons close to the Fermi surface are driven by the external temperature gradient.The filled small spheres are occupied electron states and the open small spheres are unoccupied electron states.The electrons can relax through both largeangle scatterings and small-angle scatterings(vertical processes).

The abnormal behavior of normalized Lorentz numbers in the middle temperature region in Fig.2(f)can be attributed to inelastic electron–phonon scattering.The electron scattering process in electrical and thermal transport is different,[13]as shown in Fig.3.Electrons driven by the electric field during electrical transport can only be relaxed by large-angle scattering (horizontal process), thus changing the direction of motion.Large-angle scattering can be approximated as elastic scattering,although there is little energy loss.Electrons driven by the temperature gradient during thermal transport can also relax through the large-angle scattering mechanism, in addition to the existence of an additional relaxation mode,namely small-angle scattering.Small-angle scattering is inelastic scattering and restores equilibrium by transferring some energy to the lattice.This results in a discrepancy between momentum relaxation time and energy relaxation time.With the decrease of temperature, the scattering of electrons with long wave phonons is inhibited obviously,so the scattering of electrons and short wave phonons is dominant.The scattering of short-wave phonons and electrons does not easily change the momentum of the electron, but it is easier to change the energy of the electron through the small-angle scattering process.Therefore, the energy relaxation time will be shorter than the momentum relaxation time.[14–16]

As the temperature drops further,the number of phonons decreases rapidly and electron–phonon scattering is no longer dominant.At low temperatures, electron–defect scattering is dominant.Since the effective mass of electrons is much smaller than that of defects in general,electron–defect scattering is elastic scattering.The elastic scattering relaxation times for momentum flow and energy flow are the same and do not break the WF law, so the normalized Lorentz number begins to recover.[13,14]

4.Conclusion

We have carried out the heat capacity,electrical and thermal transport measurements on CrP.By extracting the electron thermal conductivity,the thermal and electrical transport properties of CrP are compared.The normalized Lorentz number remains nearly 1 above about 160 K, but begins to decrease below 160 K due to the difference in momentum and energy relaxation time in electron–phonon inelastic scattering.The normalized Lorentz number starts to recover below 25.6 K,which comes from the fact that electron–defect scattering as elastic scattering replaces electron–phonon scattering predominates at low temperature.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.12134018, 11921004,and 11634015), the National Key Research and Development Program of China (Grant Nos.2022YFA1602800,2021YFA1401800, 2017YFA0302901, 2017YFA0302903,and 2022YFA1402203), the Strategic Priority Research Program and Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (Grant No.XDB33010100),and the Synergetic Extreme Condition User Facility(SECUF).