基于扩展PFC2D-GBM模型的单齿切削花岗岩破碎机制
黄继庆 胡海 樊思成 刘伟吉 祝效华

摘要:常規钻井工具在钻进深部油气资源地层岩石的过程中,通常会遇到钻速低、成本高等问题。为提高钻头在深部硬地层的钻进效率、优化破岩参数,利用扩展PFC2D-GBM模型建立基于真实晶粒结构的花岗岩模型,对PDC单齿切削作用下的破岩机制进行深入分析,分别从宏细观尺度讨论围压、前倾角以及切削速度对破岩效果的影响。结果表明:在切削过程中,岩石中总会萌生晶内拉伸裂纹、晶内剪切裂纹、晶间拉伸裂纹以及晶间剪切裂纹4种微裂纹;无论在何种工况下,晶间拉伸裂纹的数量总是最多且分布范围最广;在无围压时,矿物晶粒在PDC齿作用下沿晶粒边界脱离岩石形成岩屑,产生的裂纹基本是晶间拉伸裂纹,只存在极少的晶内裂纹;随着围压的增大,晶内剪切裂纹的萌生会得到一定的促进作用,并且围压越大,这种促进作用更强。
关键词:硬岩; 花岗岩; PFC2D; 细观破碎; 数值模拟
中图分类号:TE 921 文献标志码:A
引用格式:黄继庆,胡海,樊思成,等.基于扩展PFC2D-GBM模型的单齿切削花岗岩破碎机制[J].中国石油大学学报(自然科学版),2023,47(2):81-89.
HUANG Jiqing, HU Hai, FAN Sicheng, et al. Rock cutting mechanisms of granite using an extended PFC2D-GBM model[J].Journal of China University of Petroleum(Edition of Natural Science),2023,47(2):81-89.
Rock cutting mechanisms of granite using an extended PFC2D-GBM model
HUANG Jiqing1, HU Hai2, FAN Sicheng1, LIU Weiji2, ZHU Xiaohua2
(1.CNPC Bohai Petroleum Equipment Manufacturing Company Limited, Tianjin 300457,China; 2.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China)
Abstract: Low penetration rate and high cost are the main problems encountered in drilling of deep oil and gas formation using conventional drilling tools. In order to improve the drilling efficiency of drill bits in deep and hard rocks and to optimize the rock breaking parameters, a granite rock model based on real grain structures was established using an extended PFC2D-GBM model, and the rock breaking mechanisms with a PDC single-tooth were studied. The effects of confining pressure, rake angle and cutting speed on granite fragmentation were discussed at macro and micro scales. The results indicate that, in the rock cutting process, four types of micro cracks can be generated in the rock matrix,i.e. intragranular tensile crack, intragranular shear crack, intergranular tensile crack and intergranular shear crack. The number of the intergranular tensile cracks is always the largest and its distribution range is also the widest under any working conditions. When there is no confining pressure, mineral grains can be broken off from the rock matrix along the grain boundaries under the action of the PDC teeth, and the cracks generated are basically the intergranular tensile cracks, only with a few intragranular cracks. However, with the increase of the confining pressure, the initiation of intragranular shear cracks can be promoted, and the higher the confining pressure, the more of the intragranular shear cracks.
Keywords:hard rock; granite; PFC2D; meso-fragmentation; numerical simulation
作为世界能源结构的主体,石油、天然气的消耗量随着世界经济不断发展而日益增加。由于不断的开采,浅层容易被开发的常规油气资源越来越少,高效开发深层、超深层油气资源成为中国实现能源接替战略的重大需求,是当前和未来油气勘探开发的重点和热点[1-2]。油气资源的勘探开发从浅层向深层、超深层发展的过程中,钻遇硬度高、研磨性高、可钻性级值高的岩石的概率越来越大[3]。牙轮钻头、金刚石钻头等常规破岩工具在深井、超深井的钻进过程中,通常会遇到钻头磨损严重、钻井成本高等问题[4],这严重影响了深部硬地层的机械钻速,从而导致勘探开发成本大量增加。在常规破岩钻头中,PDC钻头相对于牙轮钻头等其他钻头具有较高硬度、耐磨性好、结构简单和设计灵活的特点[5],具有更大的改进空间。为提高PDC钻头在硬岩地层中的钻进效率,许多学者和专业人员进行了大量的尝试和试验[6-7],而众多数值模拟试验在钻头的设计和优化过程中功不可没[8-11]。然而,许多模拟试验大多将岩石考虑成均质结构,忽略岩石内部细观结构的影响,在一定程度上制约了对钻头结构的进一步有效优化。为进一步研究岩石在PDC齿切削作用下的破碎机制,笔者以典型的深部硬岩—花岗岩[12-13]为研究对象,引入岩石内部细观晶粒真实的结构及其分布状态,建立花岗岩扩展PFC2D-GBM模型,讨论在PDC单齿线性切削作用下,围压、前倾角以及切削速度对花岗岩破碎情况的影响,以期为PDC钻头的进一步优化以及深部油气资源的高效开采过程提供新思路、新方法。
1 花岗岩模型建立与标定
1.1 扩展PFC2D-GBM模型
破碎机制的研究必然与岩石的细观力学行为等方面有关。然而,通过室内试验只能观测到岩石的宏观力学行为,对于岩石内部微裂纹的扩展等现象却难以观测,并且室内试验无法实现完全相同条件下的重复性操作。近年来,通过数值方法再现岩石破碎的完整过程成为解决上述问题的新方法[14-16]。PFC(particle flow code)作为基于非连续介质力学的代表性软件[17],不仅可以模拟岩石材料的宏观特性和细观力学特性,而且可以很方便地揭示细观层面上岩石的动态力学特性[18]。在PFC中,岩石由微小的、离散的颗粒组成,颗粒与颗粒之间通过特定的力学接触而相互联系在一起。当有外力作用时,各个颗粒之间的接触被压缩、分离或滑动,颗粒因此会发生平移、旋转和变形,众多微小颗粒的细观力学行为汇集成岩石的宏观力学行为。为使岩石模型贴近岩石的真实结构,Potyondy[19]在PFC2D中建立了一种基于晶粒结构的复杂岩石模型(grain based model, GBM)。GBM极大的促进了对岩石细观力学行为的研究[20-21]。
基于上述模型,将传统GBM中表征晶粒形状的多边形替换为真实的花岗岩晶粒轮廓图,使模型的微观结构更贴近真实的岩石。采用的岩样来自湖北随州的花岗岩,主要矿物组分为斜长石(21.9%)、钠长石(47.5%)、石英(19.3%)以及黑云母(9.3%),其晶粒轮廓明显、矿物成分易区分。按照刘伟吉等[22]提出的方法建立基于真实晶粒轮廓的花岗岩扩展PFC2D-GBM模型。模型建立过程如图1所示。
1.2 细观参数标定
PFC中的数值模型能用于探究岩石破碎机制的前提,是必须能够再现特定的宏观力学行为。根据图1所示的过程建立非均质花岗岩模型,并按矿物种类在合理范围内赋予颗粒力学参数。通过单轴压缩试验和巴西劈裂试验获得岩石模型的抗压强度、弹性模量以及抗拉强度。用于单轴压缩试验的模型是一个矩形,其高度为50 mm、宽度为25 mm,包含35 078个颗粒;用于巴西劈裂试验的模型则是一直径为25 mm的圆,包含13 644个颗粒。标定试验的结果如图2、3所示。
两个标定试验的抗压强度为84.8 MPa、弹性模量为10 451.4 MPa、抗拉强度为5.31 MPa。通过室内试验得到抗压强度为86.37 MPa、弹性模量为10 707.6 MPa、抗拉强度为4.85 MPa。抗压强度、弹性模量、抗拉强度标定结果与试验结果间误差分别为1.82%、2.39%、9.4%,误差均小于10%,证明相关参数能用于后续试验。标定模型中颗粒的最小半径为7.5×10-5 m、最大半径为1.25×10-4 m,颗粒密度为2 700 kg/m3,摩擦系数为0.5,平行键半径倍数为1,平行键摩擦角为30°。模型中的其他微观参数[22]如表1所示。
2 切削破岩数值模拟
2.1 切削破岩模型
基于花岗岩模型,采用表1中的各项细观参数并导入PDC齿,建立如图4所示的切削破岩模型。该模型包含7 716个颗粒,长度为20 mm,高度为12 mm。PDC齿的直径为12 mm。讨论花岗岩地层处于平衡压力钻井时的破碎情况,该状态下井筒内的液柱压力与地层压力相等。将花岗岩模型的底边固定,通过两侧的刚性壁及上方的柔性边界颗粒链向其施加围压pc。两侧的刚性壁上施加的围压代表地层压力,上方柔性边界颗粒链施加的压力代表钻井过程中的液柱压力。PDC齿与岩石之间的接触不会受到柔性边界颗粒链的影响,因为PDC齿能够穿过柔性边界颗粒链与花岗岩直接接触。
2.2 結果分析
研究围压、切削速度以及前倾角对花岗岩在PDC单齿线性切削作用下破碎情况的影响。围压pc为0~6 MPa,增量为2 MPa;前倾角θ为5°~20°,增量为5°;切削速度υ为0.5~2.0 m/s,增量为0.5 m/s。PDC齿切削花岗岩的整个过程中切削深度为1 mm,切削行程为5 mm。
2.2.1 岩屑与裂纹
图5为υ=1.0 m/s时,不同pc和θ作用下花岗岩的破碎情况,图6为θ=5°时,不同pc和υ作用下花岗岩的破碎情况。图5、6展示了岩屑的生成以及不同种类裂纹的萌生和分布情况。为更好地展示岩石的破碎情况,其中未显示柔性边界颗粒链。
由图5可以看出:pc=0 MPa时产生的岩屑尺寸都比较大,并且基本沿PDC齿的切削面分布;当pc≠0 MPa时,岩屑的尺寸都比较小。在整个切削过程中,岩石中萌生晶内拉伸裂纹、晶内剪切裂纹、晶间拉伸裂纹以及晶间剪切裂纹4種微裂纹。
由图5、6可知,无论在何种工况下,总是会萌生大量的晶间拉伸裂纹,其数量最多且分布最广,晶间拉伸裂纹不仅在直接损伤区大量萌生,也广泛分布在远离直接损伤区的更深处的各晶粒边界上。pc=0 MPa时,PDC齿主要造成晶粒与晶粒之间的破坏,各晶粒在PDC齿作用下沿晶粒边界脱离岩石形成岩屑,岩屑的尺寸普遍较大。此时在直接损伤区产生的裂纹基本是晶间拉伸裂纹,只存在非常少的晶内裂纹;而随着围压增大,直接损伤区内晶内裂纹的萌生得到促进,并且围压越大,这种促进作用越强。这是由于在PDC齿将矿物晶粒从岩石上剥离后,柔性边界颗粒链向下施加的压力使PDC齿再次与岩屑相互作用,导致岩屑发生二次破碎,从而产生大量晶内裂纹。并且当pc=0 MPa、θ=5°时,切削过程产生的晶内裂纹数量最少。pc≠0 MPa时,在同一围压条件下,不同前倾角对花岗岩造成的破碎相差并不是很明显。
与图5展示的情况相似,图6中pc=0 MPa时的岩屑尺寸也普遍较大。而在同一围压条件下,不同切削速度对花岗岩造成的破坏相差并不明显。但随着围压的增大,同一切削速度下花岗岩的破碎难度增加,因为围压增大会使岩石内部的微孔隙逐渐闭合,各矿物晶粒之间变得更加致密,PDC齿对花岗岩造成破坏的难度逐渐加大。在pc没有达到极限值以前这种趋势不会发生变化。
2.2.2 切削力与裂纹变化
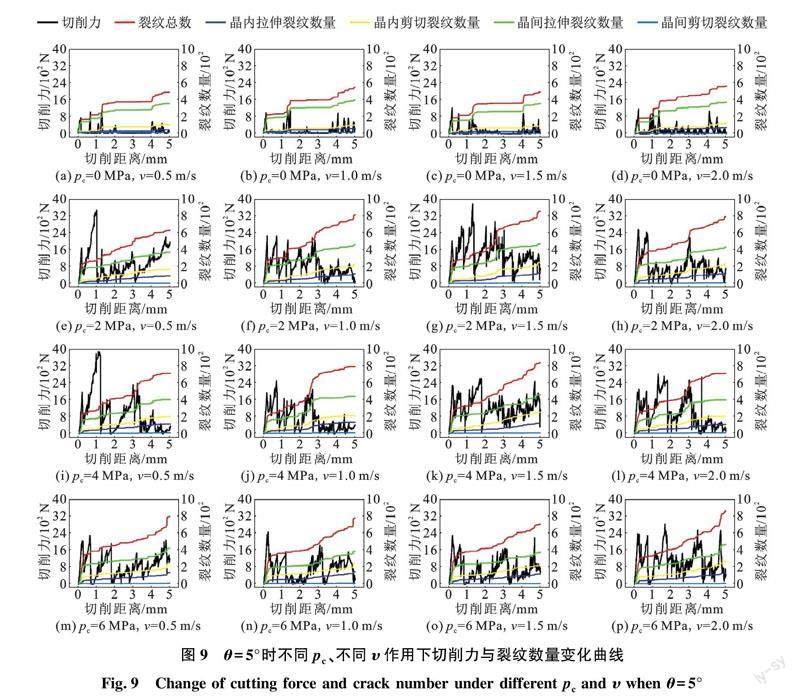
切削花岗岩的过程中PDC齿会受到岩石对其产生的作用力,即切削力。通过对PDC齿和岩石模型的动态监测,可以得到切削力以及各类型裂纹的变化情况。图7为υ=1.0 m/s时,不同pc和θ作用下切削力与裂纹数量的变化曲线。图8为切削模型局部展示。图9为θ=5°时,不同pc和υ作用下切削力与裂纹数量的变化曲线。
在pc=0 MPa的条件下,切削力变化曲线波峰的数量最少,并且波峰的峰值小,即无围压状态下切削力的频率和幅度都比较小。这是因为晶粒边界的力学参数比晶粒内部各粒子之间的力学参数弱,PDC齿对花岗岩造成的破坏主要发生在各晶粒边界处,产生的岩屑通常是整块的矿物晶粒,这与岩屑尺寸在无围压状态下普遍偏大的现象相吻合。从图9可知,pc=0 MPa时,切削力变化曲线的波峰数量会随着切削速度的增大而增多,但每个波峰的峰值并不大,这意味着PDC齿的切削速度越大,无围压状态下切削力的变化频率越高。然而,图7显示前倾角的增大又会减小切削力变化曲线的波峰数量,即前倾角的增大可以降低切削力的变化频率。另外,由图7和9可以看出,在pc≠0 MPa时,在切削行程超过3 mm后,切削力变化曲线在大多数情况下会出现明显的下降。由图8可知,当切削行程为3 mm时,PDC切削齿直接作用在3号晶粒上,而由图7与9中pc=0 MPa时的破碎情况可知,3号晶粒几乎是整块从花岗岩上脱离,因此3号与4号晶粒之间的边界比较薄弱, PDC齿极易对其造成破坏,因此造成了上述切削力变化曲线的下降。
从图7中可以看出,随着θ的不断增大,相同围压条件下切削力变化曲线中大峰值波峰的数量减小,相应地,峰值平均值减小。在θ为5°和20°时,相同围压条件下的切削力平均值最小,且波峰的分布更加均匀,这表明PDC齿受到的力最小且受力的频率更稳定,PDC齿受到的损伤最小。由图9可知,当υ=0.5 m/s时,有围压状态下切削力曲线在切削过程的初期总是会出现峰值很高的大波峰;在υ=1.5 m/s时,切削力曲线在有围压状态下的波谷在整个切削过程中始终维持在一个较高水平,PDC齿处在持续受力的状态;而与υ=1.0 m/s时的情况相比,υ=2.0 m/s时切削力曲线的波峰的峰值更大。综合切削力曲线在4个切削速度与不同围压条件下的变化情况,PDC齿在υ=1.0 m/s时受力最小。
在所有工况下,裂纹总数在切削过程初期总是会出现骤增,此时PDC齿与花岗岩之间发生相互作用,切削力出现第一个波峰。此后,裂纹总数的变化与切削力曲线波峰的变化情况直接相关:当切削力曲线出现波峰时,裂纹总数增加。在大多数情况下,波峰的峰值越大且大峰值波峰越密集时裂纹总数的增加越明显。而当切削力曲线不出现波峰或波峰的峰值处于较低水平时,各种类型的裂纹数量几乎不发生变化。晶内剪切裂纹与晶间拉伸裂纹的数量与裂纹总数变化趋势一致,
不同工况下晶间拉伸裂纹的数量与裂纹总数变化趋势一致。
4种微裂纹中,晶间拉伸裂纹的数量从始至终都处在最高水平,晶内剪切裂纹的数量次之,晶内拉伸裂纹数量始终处于较低水平,而晶间剪切裂纹数量基本为0且几乎没有变化。当其他条件相同时,晶内剪切裂纹的数量总是会随围压的增大而增大。晶内拉伸裂纹与晶间拉伸裂纹随围压的变化规律不太明显。
综上可知,围压的增大会促进晶内剪切裂纹的萌生,并且当υ=1.0 m/s时,在θ=5°与θ=20°的情况下,切削力的最大峰值相对其他情况更小,且波峰分布更加平均,此时PDC齿受力最小且受力频率更稳定。
2.2.3 破碎比
为进一步描述花岗岩的破碎情况,引入破碎比K来表示花岗岩在切削过程受到的破坏,K的计算公式为
K=Sd/St.
式中,Sd为发生破坏的颗粒总面积,m2;St为整个模型包含的所有颗粒的面积总和,m2。
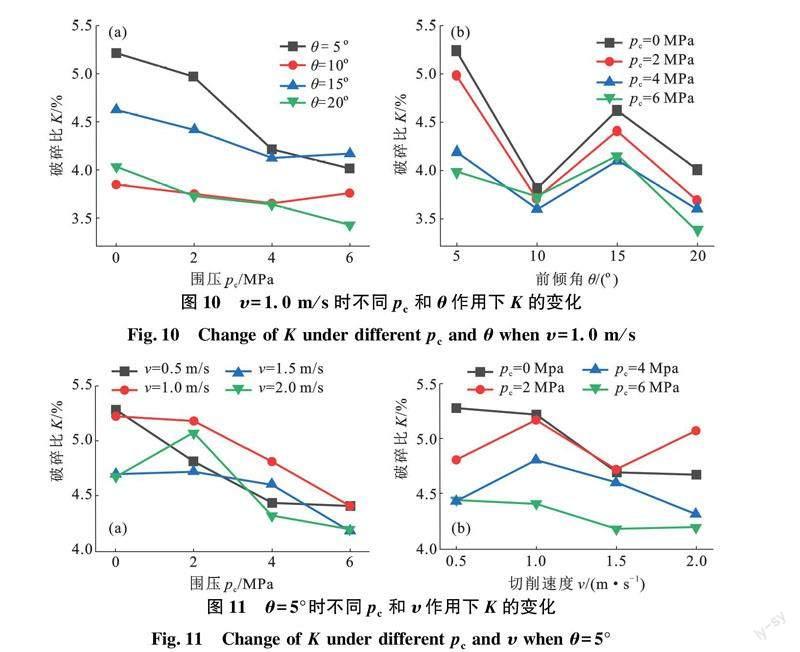
图10为υ=1.0 m/s时不同pc和θ作用下破碎比的变化情况。由图10(a)可以看出,不同切削角度下的破碎比随着围压的增大而减小。这是由于随着围压的增大,岩石内部的微孔隙逐渐闭合,各矿物晶粒之间变得更加致密,PDC齿对花岗岩造成破坏的难度逐渐加大。而在pc没有达到极限值以前,这种趋势不会发生变化。由图10(b)可以看出,相同围压条件下破碎比随θ的增大呈波浪式变化,即K随θ的增大先减小后增大,然后再减小。在不同工况下,θ=5°时的破岩效率最高。
图11为θ=5°时不同pc和υ作用下K的变化情况。由图11(a)可以看出,同一围压条件下,不同切削速度的破碎比随着围压的增大而有不断减小的趋势,这与图10中情况相似,都是由于岩石内部的微孔隙随着围压的增大而逐渐闭合造成的。相對于其他3种切削速度,υ=1.0 m/s时的K大多数情况下都是最大的。由图11(b)可以看出,同一围压条件下切削速度的改变对破碎比的改变并不明显。在没有围压时,切削速度的增加会导致破碎比逐渐减小。
3 结 论
(1)在整个切削过程中,岩石中会萌生晶内拉伸裂纹、晶内剪切裂纹、晶间拉伸裂纹以及晶间剪切裂纹4种微裂纹。其中晶间拉伸裂纹数量最多且分布最广,不仅在直接损伤区大量萌生,也广泛分布在远离直接损伤区的更深处的各晶粒边界上。
(2)不存在围压时,PDC齿主要造成晶粒之间的破坏,矿物晶粒在PDC齿作用下沿晶粒边界脱离岩石形成岩屑,此时产生的裂纹基本是晶间拉伸裂纹,只存在很少的晶内裂纹。而随着围压的增大,晶内剪切裂纹的萌生会得到一定的促进作用,并且围压越大,这种促进作用越强。
(3)当υ=1.0 m/s、θ=5°时,PDC齿受力最小且受力的频率更稳定,并能保证较高的破岩效率。
参考文献:
[1]陈浩,李邦润,蔡灿,等.深井高温岩石破岩机理及生热分析[J].石油机械,2021,49(1):1-10.
CHEN Hao, LI Bangrun, CAI Can, et al. Rock breaking mechanisms and heat generation analysis on high temperature rocks in deep wells[J]. China Petroleum Machinery, 2021,49(1):1-10.
[2]胡文瑞,鲍敬伟.石油行业发展趋势及中国对策研究[J].中国石油大学学报(自然科学版),2018,42(4):1-10.
HU Wenrui, BAO Jingwei. Development trends of oil industry and Chinas countermeasures[J].Journal of China University of Petroleum(Edition of Natural Science),2018,42(4):1-10.
[3]黄家根,汪海阁,纪国栋,等.超声波高频旋冲钻井技术破岩机理研究[J].石油钻探技术,2018,46(4):23-29.
HUANG Jiagen, WANG Haige, JI Guodong, et al. The rock breaking mechanism of ultrasonic high frequency rotary-percussive drilling technology[J]. Petroleum Drilling Techniques, 2018,46(4):23-29.
[4]王滨,邹德永,李军,等.深部及复杂地层中PDC钻头综合改进方法[J].石油钻采工艺,2018,40(1):44-51.
WANG Bin, ZOU Deyong, LI Jun, et al. A comprehensive method to improve the performance of PDC bits in deep and complex formations[J]. Oil Drilling & Production Technology, 2018,40(1):44-51.
[5]唐胜利,曹小军,高欣,等.PDC切削齿后倾角与破岩关系的数值模拟[J].煤炭技术,2019,38(4):154-157.
TANG Shengli, CAO Xiaojun, GAO Xin, et al. Numerical simulation of relationship between back rake of PDC cutter and rock breaking[J]. Coal Technology, 2019,38(4):154-157.
[6]邹德永,蔡环.布齿参数对PDC钻头破岩效率影响的试验[J].中国石油大学学报(自然科学版),2009,33(5):76-79.
ZOU Deyong, CAI Huan. Experiment on effect of cutter parameters of PDC bit on rate of penetration[J].Journal of China University of Petroleum(Edition of Natural Science), 2009,33(5):76-79.
[7]王家骏,邹德永,杨光,等.PDC切削齿与岩石相互作用模型[J].中国石油大学学报(自然科学版),2014,38(4):104-109.
WANG Jiajun, ZOU Deyong, YANG Guang, et al. Interaction model of PDC cutter and rock[J].Journal of China University of Petroleum(Edition of Natural Science), 2014,38(4):104-109.
[8]祝效华,但昭旺.PDC切削齿破碎干热岩数值模拟[J].天然气工业,2019,39(4):125-134.
ZHU Xiaohua, DAN Zhaowang. Numerical simulation of rock breaking by PDC cutters in hot dry rocks[J]. Natural Gas Industry, 2019,39(4):125-134.
[9]祝效华,李海.PDC切削齿破岩效率数值模拟研究[J].应用基础与工程科学学报,2015,23(1):182-191.
ZHU Xiaohua, LI Hai. Numerical simulation on mechanical special energy of PDC cutter rock-cutting[J]. Journal of Basic Science and Engineering, 2015,23(1):182-191.
[10]马清明,王瑞和.PDC切削齿破岩受力的试验研究[J].中国石油大学学报(自然科学版),2006,30(2):45-47.
MA Qingming, WANG Ruihe. Experimental study on force of PDC cutter breaking rock[J]. Journal of China University of Petroleum(Edition of Natural Science), 2006,30(2):45-47.
[11]景英华,袁鑫伟,姜磊,等.高速旋转冲击钻井破岩数值模拟及现场实验[J].中国石油大学学报(自然科学版),2019,43(1):75-80.
JING Yinghua, YUAN Xinwei, JIANG Lei, et al. Numerical simulation and field experimental study on rock breaking in high speed rotating percussion drilling[J]. Journal of China University of Petroleum(Edition of Natural Science),2019,43(1):75-80.
[12]宫凤强,伍武星,李天斌,等.深部硬岩矩形隧洞围岩板裂破坏的试验模拟研究[J].岩土力学,2019,40(6):2085-2098.
GONG Fengqiang, WU Wuxing, LI Tianbin, et al. Simulation experimental study of spalling failure of surrounding rock of rectangular tunnel of deep hard rock[J]. Rock and Soil Mechanics,2019,40(6):2085-2098.
[13]李地元,胡楚维,朱泉企.预制裂隙花岗岩动静组合加载力学特性和破坏规律试验研究[J].岩石力学与工程学报,2020,39(6):1081-1093.
LI Diyuan, HU Chuwei, ZHU Quanqi. Experimental study on mechanical properties and failure laws of granite with an artificial flaw under coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Engineering, 2020,39(6):1081-1093.
[14]祝效华,刘伟吉.楔形钻齿作用下岩石破碎及微观劣化过程[J].中国石油大学学报(自然科学版),2017,41(1):90-95.
ZHU Xiaohua, LIU Weiji. Numerical simulation of rock breaking and microscopic deterioration under wedge-shaped drill bit teeth[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(1):90-95.
[15]FAIRHURST C. Rock engineering: where is the laboratory?[J]. Rock Mechanics and Rock Engineering, 2019,52(12):4865-4888.
[16]趙吉坤,张子明,仝兴华,等.岩石宏细观弹塑性损伤破坏对比研究[J].中国石油大学学报(自然科学版),2007,31(4):78-84.
ZHAO Jikun, ZHANG Ziming, TONG Xinghua, et al. Comparison of macro-scale and meso-scale elasto-plastic damage failure in rocks[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007,31(4):78-84.
[17]CUNDALL P A, STRACK O D L. A discrete numerical mode for granular assemblies[J]. Géotechnique, 1979,29(1):
47-65.
[18]HUANG Haiying, DETOURNAY E. Discrete element modeling of tool-rock interaction II: rockindentation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013,37(13):1930-1947.
[19]POTYONDY D O. A grain-based model for rock: approaching the true microstructure: Proceedings of Bergmekanikki Norden 2010—Rock Mechanics in the Nordic Countries 2010[C]. Kongsberg: Norwegian Group for Rock Mechanics, 2010.
[20]ZHOU Jian, LAN Hengxing, ZHANG Luqing, et al. Novel grain-based model for simulation of brittle failure of alxa porphyritic granite[J]. Engineering Geology, 2019,251:100-114.
[21]SAADAT M, TAHERI A. A numerical approach to investigate the effects of rock texture on the damage and crack propagation of a pre-cracked granite[J]. Computers & Geotechnics, 2019,111:89-111.
[22]劉伟吉,胡海,祝效华,等.围压条件下电脉冲破碎干热岩机理[J].天然气工业,2022,42(4):117-129.
LIU Weiji, HU Hai, ZHU Xiaohua, et al. Breaking mechanisms of hot dry rock by electric pulse under confining pressure[J]. Natural Gas Industry, 2022,42(4):117-129.
(编辑 李志芬)
收稿日期:2022-09-20
基金项目:国家能源局能源领域“科技助力经济2020”重点专项(9);国家自然科学基金项目(52004229)
第一作者:黄继庆(1969-),男,教授级高级工程师,硕士,研究方向为石油机械技术开发和管理。E-mail:huangjiqing@cnpc.com.cn。
通信作者:刘伟吉(1989-),男,副教授,博士,研究方向为高效破岩理论与方法、钻井提速提效技术。E-mial;lwj2017_swpu@163.com。

