液体火箭上升段制导方法的发展综述*

李惠峰,张 冉,王嘉炜

北京航空航天大学宇航学院,北京 100191

0 引言

火箭制导的任务是控制火箭的质心运动,即根据导航提供的飞行时间和飞行状态产生推力和姿态控制指令,使火箭达到期望的终端状态。现有文献中的制导一词可从2种角度理解:从狭义角度,其特指火箭控制系统中的制导律,即实现期望飞行轨迹的控制规律和策略;从广义角度,制导涵盖了火箭任务轨迹和飞行策略的设计,是一门研究如何“管理”轨迹的学科。本文从狭义角度出发,介绍液体火箭上升段制导方法的发展历程,并展望其未来的发展方向。

运载火箭上升段制导是一门历史悠久的学科。第二次世界大战期间,德国“V-2”火箭就搭载了惯性导航器件,通过调整火箭姿态和发动机关机时间控制火箭的飞行轨迹,初步形成了制导的概念。第二次世界大战后,各国的航天计划进一步推动了上升段制导的发展,逐渐形成了大气层内摄动制导、大气层外显式制导的飞行策略,这一策略迄今为止仍被广泛使用[1]。21 世纪以来,深空探测和载人航天等任务对制导方法的智能自主性、任务适应性和故障适应性提出了更高的要求。而控制理论、数值计算、机器学习等领域的突破和箭载计算能力的增强为制导方法的进一步发展提供了坚实的基础。智能制导、计算制导等概念已吸引了国内外研究人员的广泛关注[2-7]。基于数值规划和强化学习的上升段制导方法可能迎来新的突破。

然而,上升段制导亦是一门对可靠性要求极高的学科。经过多次飞行试验的成熟制导方法一般得到长期沿用。上世纪60至70年代提出的迭代制导和动力显式制导至今仍是主要的大气层外制导方法[1,6,8]。例如,美国正在开发的空间发射系统(SLS)就使用了航天飞机的动力显式制导方法,并复用了部分程序代码[9-10]。事实上,当现有制导方法的功能和性能可以满足任务要求时,新的制导方法一般难以得到应用。在这样的学科背景下,上升段制导的几次变革显得尤为突出,一般带来了制导功能或性能上的突破。为分析变革原因,并展望未来潜在的突破方向,本文整理了上升段制导发展的背景和驱动力。一般来说,上升段制导的发展离不开3个因素:飞行任务需求、控制计算理论、箭载计算平台。

首先,让火箭的运载能力更强、飞行更安全、成本更低是火箭总体设计的一项主要目标[4]。在控制系统层面,这构成了上升段制导发展的主驱动力。近年来,总体设计对上升段制导的性能(特别是故障适应性)提出了越来越高的要求[11-13]。而火箭设计亦受益于上升段制导功能上的突破。例如,具有主动减载能力的制导方法能够降低火箭所受的气动载荷,进而降低结构质量;具有终端姿态调节能力的制导方法能够省去火箭末级的调姿系统。先进的制导方法不仅是实现标称飞行轨迹的工具,还能够在一定程度上缓和火箭任务设计中的矛盾,直接或间接地增强火箭各项指标。

其次,上升段制导上游学科(包括控制理论和数值计算)的发展提供了新的理论工具。以最优控制理论为例,它一方面为大气层内摄动制导提供了标称轨迹的离线优化算法,另一方面为分析火箭最优轨迹性质提供了理论基础,支撑了大气层外显式制导的设计和性能评估。而火箭轨迹规划问题的数值求解方法,从早期的梯度法到上世纪末的序列二次规划和凸内点法,亦取得了长足的进步[14-15]。数值方法能够在越来越短的时间内求解越来越复杂的火箭轨迹规划问题,为在线轨迹规划[16-21],和基于闭环轨迹优化的制导方法提供了基础[22-25]。

最后,箭载计算平台的运算能力大幅上升。运算能力曾是过去制约制导方法复杂度的一项因素,如今已成为应用先进制导技术的驱动力。随着箭载计算机的核心数量、浮点计算效率的提升,以及并行处理单元、现场可编程门阵列(FPGA)等硬件计算设备规模的扩大,箭载计算平台能够提供的算力已经远远超出了经典制导方法的需要。如何充分应用这些算力增强制导的智能自主性成为了一项研究热点,特别是推动了机器学习在制导中的应用[7,26-30]。

考虑到大气层内外火箭质心运动特性和制导的主要设计目标存在差异,而大气层内外的制导策略亦存在较大差异,本文将分别介绍大气层外和大气层内制导方法的发展历程。

1 大气层外制导方法的发展

运载火箭的制导技术发展自上世纪50年代的弹道导弹制导技术,如“阿特拉斯”导弹采用的Delta制导方法和“雷神”导弹采用的Q制导方法[31]。这些制导方法依赖于离线规划的标称轨迹。早期的运载火箭,如“红石”运载火箭,亦采用了依赖标称轨迹的Delta最小化制导方法,通过不断修正火箭轨迹和标称轨迹的偏差来控制火箭飞行[32]。这些制导方法的计算公式简单,可应用当时的模拟计算机实现。需要指出的是,模拟计算机的计算精度对制导精度有着直接影响。以“雷神”导弹为例,关键参数每百分之一的偏差都可能导致约6.4 km的落点偏差。因此,“雷神”导弹对于3 km的精度要求直接决定了模拟计算精度的要求。此外,对标称轨迹的依赖性使得这些制导方法难以适应强大气扰动和推力故障,其控制精度和燃料最优性未能满足载人航天任务的要求。

上世纪60年代出现的显式制导概念提供了另一种制导思路。显式制导建立了制导指令和终端目标间的显式关系,根据火箭当前的飞行状态,规划火箭未来的飞行轨迹以生成制导指令[33-34]。显式制导的开发受益于箭载数字计算机的应用,一方面导航系统对完整飞行状态(位置和速度)的解算更加容易,另一方面解除了制导设计中对代数运算和迭代计算的限制。基于显式制导概念的大气层外制导方法如图1 所示。

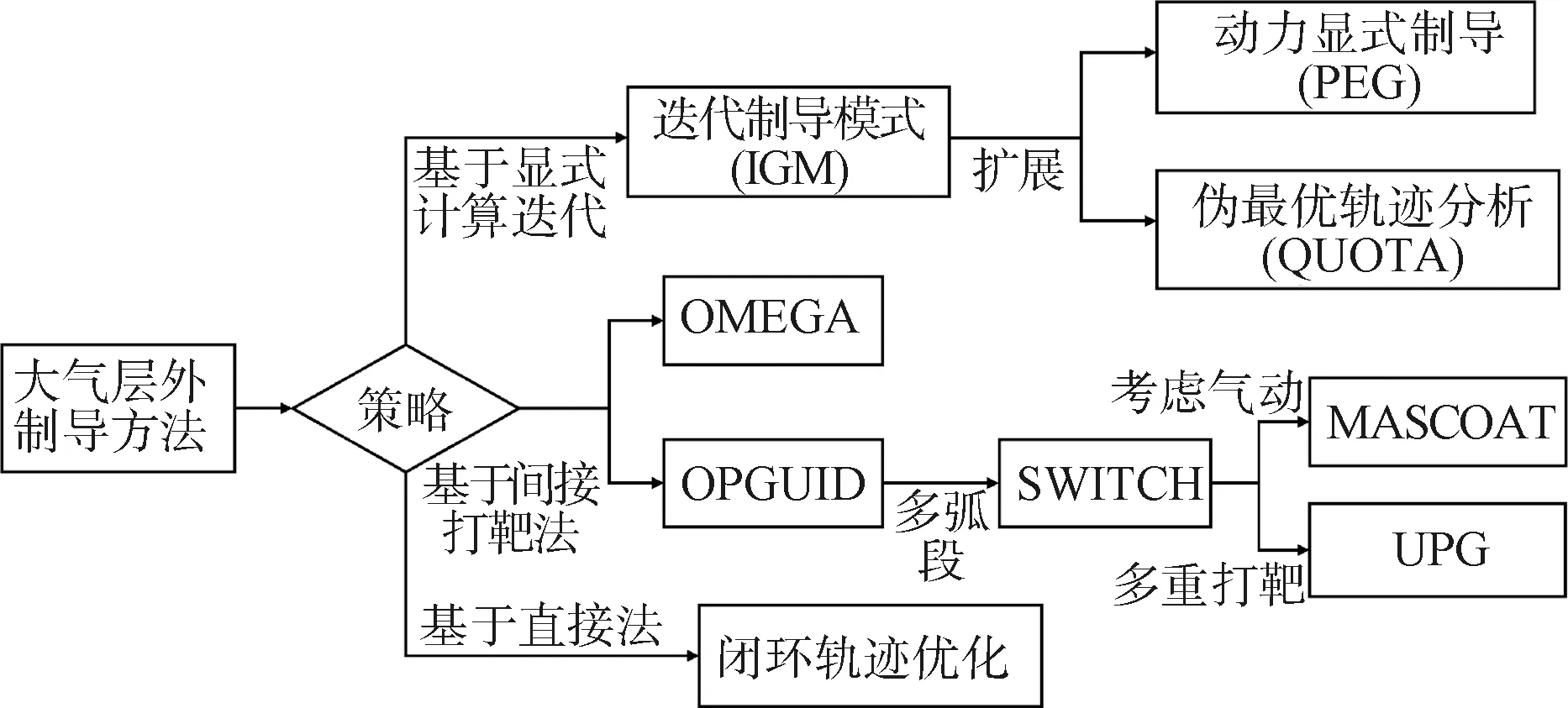
图1 大气层外制导方法的发展

1.1 迭代制导模式

迭代制导模式 (Iterative Guidance Mode,IGM) 是 NASA 于上世纪 60 年代为运载火箭开发的一系列制导方法,其中包括“土星五号”运载火箭采用的迭代制导方法[35-36]。迭代制导是一种路径自适应动力制导方法:不是去跟踪离线规划的标称轨迹,而是时刻根据当前位置和速度规划一条新的最优轨迹。基于线性程序角和平均重力场假设,最优轨迹的生成和制导指令的反解具有解析或半解析的形式,因此能够应用当时的箭载计算机实现。此外,迭代制导采用的线性程序角具有近似最优的性质,制导的燃料消耗接近最优轨迹[37]。在“土星”系列运载火箭上的数值实验显示,与最优参考相比,迭代制导多消耗的燃料通常不超过4%;在地月转移任务的多类单项偏差作用下中,近地点误差的平均值约为10 km,轨道倾角误差的平均值约为0.5°。迭代制导的燃料最优性和高制导精度为“阿波罗”系列任务的执行提供了支持,并使迭代制导成为了一种常见的上升段制导方法[38]。

迭代制导的一个主要公式是对程序角指令的分解,以俯仰通道为例:

(1)

葡萄籽原花青素对阿尔茨海默病模型大鼠学习记忆能力的改善作用及其机制研究 ……………………… 陈 伟等（13）：1760

从计算角度考虑,迭代制导的计算过程具有内外层结构:内层迭代搜索飞行时间;外层迭代搜索入轨点。内外环迭代一般均可在较少次数内收敛,而每次迭代只涉及到显式公式的计算,因此迭代制导具有较高的计算效率。考虑迭代制导的收敛性,内环迭代的收敛性与火箭推重比相关,而外环迭代的完整收敛性分析尚未见公开报道。尽管如此,迭代制导在数值算例中表现出了非常好的收敛性,并且迭代初值因具有明确的物理意义而容易设置,因此在工程中得到了广泛的应用。

国内亦展开了迭代制导的相关研究,研究成果见文献[40-43]。我国在“长征二号F”运载火箭遥八任务中首次使用了迭代制导方法,满足了空间交会对接任务对入轨精度的高要求[44-45]。随后,迭代制导应用到我国多款运载火箭上,验证了制导效果。国内研究团队对迭代制导提出了多种改进策略。例如,文献[46-50]研究了含有入轨姿态约束的制导问题,提出了同时控制入轨位置、速度和姿态的迭代制导方法。文献[51-53]研究了迭代制导在月面上升段和空间变轨任务中的扩展应用。文献[54]研究了多段接力迭代制导的应用方法。

在迭代制导的设计过程中,所做的另一个关键假设是重力加速度为常数,一般取为当前位置和预测入轨点处重力加速度的均值[36,39]。在火箭推重比较大而推进弧较短时,这一假设对燃料最优性的影响很小。然而,在火箭推重比较小且推进弧较长时,迭代制导的性能会下降,甚至出现迭代发散的现象。此时可通过设置中间目标轨道的方式实现制导,但这可能导致制导指令的跳变和燃料最优性的损失。此问题在后续开发的动力显式制导中得到了改进。

1.2 动力显式制导

动力显式制导 (Powered Explicit Guidance,PEG)是NASA在上世纪70年代为航天飞机开发的显式制导方法,历经多次改进后,在SLS上亦得到应用[8,55]。航天飞机的任务样式较土星五号更为多样,且部分任务中火箭推重比很低,可能导致迭代制导的性能下降甚至迭代发散。例如,在航天飞机的入轨和离轨过程中,推重比可能低至0.02～0.06,推进时间可能长达20 min,给迭代制导的收敛带来严峻的挑战。为此,NASA开展了多种制导算法的论证工作,在与最优制导(OPGUID)、伪最优轨迹分析(QUOTA)等制导方法的对比中,线性正切制导(Linear Tangent Guidance,LTG)受到了关注[56]。后来,Draper实验室基于LTG概念实现的一种制导方法被命名为动力显式制导,成为了航天飞机大气层外飞行的统一制导方法。

动力显式制导的一个主要公式是推力方向的线性正切变化:

(2)

图2 动力显式制导的线性正切规律

动力显式制导的一个特点是算法流程的模块化:与计算公式紧密耦合的迭代制导不同,动力显式制导可划分为多个功能具体的模块。通过改变各个模块的实现,动力显式制导可更好地适应具体的飞行任务[57]。例如,在推重比较低导致制导性能不佳时,可通过设计推力作用的预测模块予以修正[58]。此外,在航天飞机应用的动力显式制导中探索了数值方法的箭载应用:重力作用的预测采用了一种定步数数值积分方法[55]。与只使用解析公式的迭代制导不同,部分使用数值技术的动力显式制导具有更好的任务适应性[56]。

1.3 数值最优制导

最优制导是以某种最优规律产生推力和姿态指令的制导方法。闭环轨迹优化是一种较容易实现的最优制导策略:不断应用当前的飞行状态计算最优轨迹,再应用最优轨迹解中的控制量作为制导指令。尽管最优控制量的应用形式可为开环,最优轨迹的不断更新形成了一个闭环,使此类制导方法能够较好地适应飞行中的干扰和故障。另一种最优制导策略是邻近最优控制,应用最优轨迹上的敏感度矩阵直接形成反馈控制[59]。最优轨迹的计算一般依赖数值技术。

最优制导(OPGUID)是早期的一种最优制导方法,它实现了最优控制中的间接打靶法,通过猜测协态初值、计算最优轨迹、校正终端偏差的策略求解燃料最优轨迹规划问题[60]。OPGUID开发了一种最优轨迹的解析积分方法和一种定制化的牛顿法,在数值实验中表现出了良好的收敛性和收敛速度,长期作为候选制导方法与动力显式制导竞争[8]。然而,OPGUID的计算效率低于动力显式制导:在当时的地面大型机(IBM 7094)上,OPGUID的每次迭代需要0.5 s,而轨迹收敛一般需3～6次迭代。这限制了OPGUID在航天飞机上的实时应用。OPGUID后来发展形成了SWITCH制导方法,可对多推进弧、多滑行弧的火箭轨迹进行实时规划,然而多弧段的SWITCH制导方法存在收敛性问题[61]。为增强此类方法的收敛性,文献[62]提出了一种基于多重打靶法的制导方法,通过将火箭轨迹划分为多个阶段,降低了迭代对初值的敏感性。限制此类制导方法实际应用的一个主要原因是:与迭代制导和动力显式制导不同,迭代初值中的协态量缺乏物理意义,取值范围较大且难以设计系统的生成方法。

近年来,出现了应用最优控制中直接法的最优制导方法。直接法是指应用离散化方法将火箭轨迹规划问题转化为非线性规划问题并求解。此类方法形成的非线性规划问题一般具有中大规模(数百至数千个规划变量)和问题矩阵稀疏的特点。随着能够利用稀疏性的非线性规划方法(如序列二次规划方法和序列凸规划方法)发展和箭载浮点计算能力的进步,直接法已应用在各种火箭轨迹规划问题中[63]。例如,文献[64]提出了一种应用伪谱法实现闭环轨迹优化的制导方法。文献[65-66]提出了一种面向火箭上升段轨迹规划的牛顿-康托维奇方法。文献[67]提出了火箭动力故障下的救援轨道生成方法。文献[68]提出了一种能够处理阶段时长约束的多阶段轨迹规划方法。与OPGUID等基于间接打靶法的方法相比,直接法的一个优势是迭代初值的选择均具有物理意义,而协态量等对偶变量由底层的数学规划方法自行处理。基于直接法的闭环轨迹优化是一种很有前景的制导策略,但仍有收敛性、稳定性、解的存在性等问题需要进一步的分析。

2 大气层内制导方法的发展

运载火箭在稠密大气中飞行时,箭体结构、姿态控制、伺服系统均面临着较大的压力。作为细长体的火箭对气动载荷(如动压攻角积)非常敏感,在穿越大风区时,飞行控制系统的首要任务是降低箭体结构承受的载荷,而非控制轨迹误差。其次,姿态控制系统的设计和分析一般也是沿标称轨迹开展,大幅改变火箭飞行剖面可能带来不必要的风险。再次,大气层外的闭环制导方法对初始状态偏差具有较强的适应能力,使得大气层内的飞行对终端入轨精度的影响较小。上述特点在一定程度上限制了显式制导在大气层内的应用。目前大气层内的主要制导方法是基于标称轨迹的摄动制导方法,有时还辅以减载策略来进一步降低气动载荷。

2.1 摄动制导

运载火箭在大气层内飞行时,常应用摄动制导方法[69]。摄动制导方法的姿态角指令分为2部分:标称项和导引项。标称项来自离线规划的标称轨迹,选择1个自变量(如时间、高度、速度或马赫数)应用离线设计的插值表计算得到。以高度或速度作为自变量时,产生的轨迹散布可能较以时间为自变量时更小[1]。摄动制导的导引项则是根据摄动方程得到,通过在标称轨迹处线性化火箭运动方程形成反馈,控制火箭在标称轨迹附近飞行。

为降低火箭在跨声速段和最大动压段所受的气动载荷,大气层内制导中可加入减载策略。减载策略主要分为2类:离线减载和在线减载。离线减载通过在标称轨迹设计中考虑风场影响,从而降低火箭在跨声速段和最大动压段的气流攻角。文献[70]提出了一种高空风弹道修正方法,根据运载火箭发射前气象部门预测的风场信息修正飞行弹道,有效降低了“长征二号 E”运载火箭在几次飞行任务中的气动载荷。在线减载是根据火箭飞行中实时量测估计得到的过载或攻角进行反馈控制。文献[71-72]介绍了我国运载火箭使用的几种在线减载方法,包括基于攻角反馈、过载反馈和自抗扰控制的减载方法。此类方法的一个研究重点是如何取舍减载效果和轨迹精度。

2.2 闭环轨迹优化

部分任务对大气层内上升段制导的性能提出了更高的要求:一方面,这些任务对大气层内箭体分离时的飞行状态提出了约束,而摄动制导产生的状态散布可能不满足任务要求[73];另一方面,这些任务对火箭能量利用的最优性提出了较高要求,若应用反馈方法跟踪标称任务剖面,在强大气扰动下分离点的速度可能不满足任务要求。闭环轨迹规划为解决此类火箭的制导问题提供了一条可行的技术路线,通过在线规划推力和气动力复合作用下的飞行轨迹实现制导。例如,文献[74-75]提出了一种邻近-牛顿-康托维奇方法,能够实时规划火箭大气层内的轨迹,进而实现运载火箭上升段的终端速度最优制导。

可见,运载火箭大气层内的上升段制导问题具有强约束、强扰动的特征[76-77]。考虑到非线性气动力的作用,显式制导方法的设计具有一定的挑战性。然而在现有箭载计算能力的支持下,闭环轨迹优化和强化学习在此问题上均具有较好的应用潜力,有望进一步增强运载火箭对强大气扰动和故障的适应能力[3,78-81]。

3 总结与展望

介绍了运载火箭大气层内外制导方法的发展历程。上世纪提出的迭代制导、动力显式制导和大气层内的摄动制导目前仍是主要的制导方法。但近年来,火箭任务设计要求制导方法具有更强的智能自主性,从而更好地处理飞行中的强大气扰动和各类故障。这些要求为先进控制和数值计算方法在运载火箭上的应用提供了机遇。未来的上升段制导方法可能具有以下特点:

1)走向智能化。随着火箭设计(特别是动力系统和伺服系统)愈加复杂,在上升段制导系统中枚举所有可能故障并作相应处理愈发困难。亟需一种兼具感知、理解、决策、学习、适应能力的上升段制导方法,从而充分发挥火箭能力。

2)应用可靠的数值计算方法。随着数学规划求解器的数值稳定性提升,以及迭代求解火箭轨迹规划问题的理论进步,在箭载环境中使用甚至依赖数值计算进行上升段制导的条件逐渐成熟。若闭环轨迹优化的计算时间能够降低至毫秒量级,并且具有明确的收敛性保障,则有望成为一种系统且可靠的闭环制导策略,实现大气层外乃至大气层内的闭环最优制导。

3)与箭载计算设备深度融合。现有的制导方法一般未能充分利用箭载的异构计算资源,例如并行处理器与FPGA。充分应用箭载计算能力的制导方法可能在制导性能和计算效率上具有显著优势。

4)对未知干扰的估计和抑制能力。火箭上升段飞行中遇到的干扰,例如风干扰,常具有一定的结构特征,依高度的变化存在一定规律。根据干扰的结构特征对干扰进行估计甚至预测是改善上升段制导性能的一项关键手段。

综上所述,先进制导方法和箭载计算能力的结合有望进一步推动火箭控制系统的智能化、自主化,为下一代运载火箭保驾护航。