智能汽车轨迹跟踪控制算法研究综述
李松
(重庆交通大学机电与车辆工程学院,重庆400074)
缩略语
PP Pure Pursuit
PID Proportional Integral Derivative
LQR Linear Quadratic Regulator
MPC Model Predictive Control
ESO Extended State Observer
SMC Sliding Mode Control
ADRC Active Disturbance Rejection Control
FC Fuzzy Control
AC Adaptive Control
KF Kalman Filter
EKF Extended Kalman Filter
UKF Unscented Kalman algorithm
CKF Cubature Kalman Filter
PF Particle Filter
DL Deep Learning
RL Reinforcement Learning
CNN Convolutional Neural Network
PSO Particle Swarm Optimization
ILC Iterative Learning Control
DDPG Deep Deterministic Policy Gradient
0 引言
智能汽车研发是汽车产业向智能化转型的核心,智能汽车核心技术研发也得到了学术界和产业界广泛和高度的关注。智能汽车不仅能实现基础的驾驶动作,还能规避人为不良驾驶操作,大幅度降低安全风险,极大程度地减少交通事故发生率,同时也改善城市交通拥堵状况。智能汽车发展趋势不可逆转,由计算机、人工智能和控制工程等多学科领域共同发力,为中国智能汽车产业贡献高新技术和创新发展新方案。轨迹跟踪控制是智能汽车的核心技术之一,其本质是使智能汽车按照所设定的路径行驶,同时确保智能汽车操控稳定与安全。轨迹跟踪控制技术确保并期望改善智能汽车行驶舒适性和平稳性。
智能汽车的跟踪分为路径跟踪和轨迹跟踪2类[1]。不同之处是,路径跟踪问题中的参考轨迹是相对独立的,与时间关系不密切。而轨迹跟踪问题中,参考轨迹与时间密切相关,且对智能汽车随时间的响应速度和轨迹误差精度要求更高。为此,研究人员就不得不将轨迹和时间与空间建立密切关联,以保证轨迹跟踪过程的实时性,因此必须将智能汽车横向和纵向运动都与时间建立关系,从而实现智能汽车横向和纵向运动协调一致,使得智能驾驶行驶时能够迅速且平稳地按照参考轨迹运行。
本文以跟踪控制为重点研究对象,主要从基于几何运动学和动力学的跟踪控制算法及其优化方向进行研究,通过例举法和对比法,详细分析目前通用的跟踪控制方法原理及其优缺点,直观感受各种方法的试用范围和情景。
1 智能汽车轨迹跟踪算法
智能汽车的轨迹跟踪定义为:在车辆中,通常将质心(或后轮中心)选作控制点,由轨迹规划模块选择出当前时刻期望轨迹上的一个点作为合适的参考点,计算相应的速度、横向误差,使得控制点向参考点逼近,从而完成对期望轨迹跟踪过程[2],轨迹跟踪模型见图1。

图1 轨迹跟踪模型[2]
智能车辆的轨迹跟踪主要分为2类:(1)单纯基于几何运动学的跟踪算法,如纯跟踪算法(Pure Pursuit,PP)和斯坦利(Stanley)算法;(2)基于运动学模型和动力学模型的跟踪算法,如比例积分控制(Proportional Integral Derivative,PID)、线性二次调节器(Linear Quadratic Regulator,LQR)、模型预测控制(Model Predictive Control,MPC)、滑模控制和自抗扰控制等。表1中按轨迹跟踪算法分类,对当前轨迹跟踪控制和优化算法进行了总结。

表1 轨迹跟踪控制及优化算法
运动学是从几何学的角度对物体的运动规律进行分析,它包含了物体在空间中的速度和位置随时间而发生的改变。所以,车辆运动学模型可以反映车辆位置、速度、加速度与时间的关系。在建立汽车运动学模型时,必须综合考虑汽车的横向位置信息和汽车的偏航角。汽车动力学建模必须要考虑到汽车与路面间的作用力,考虑轮胎的侧偏特性。在高速行驶条件下,汽车运动学模型推导中,汽车前后车轮的运动轨迹与车轮的速度矢量不再一致。动力学模型比运动学模型增加了动态参数,更能表征汽车实际运行状态,因此,采用动力学模型对车辆的轨迹跟踪十分必要。
基于几何与运动学的跟踪算法常只适用于智能汽车车速<70 km/h 时轨迹跟踪,当车速≥70 km/h 时往往采用基于动力学以及考虑其他算法进行轨迹跟踪,如多算法融合、多约束等来提高精度与保证操纵稳定性。
1.1 纯跟踪算法(PP)
纯跟踪控制算法是一种典型的横向控制方法,最早由卡内基梅隆大学学者Wallace在20世纪八十年代提出[3],该方法对外界的鲁棒性较好。PP 算法利用期望路径与行驶路径的距离偏差来测量汽车位置信息、前轮转向角数据,来实现智能汽车的路径跟踪。纯跟踪算法具有实现简单、数据计算直观的优点,在跟踪过程中呈现出很好的鲁棒性。图2给出了纯跟踪算法控制的几何关系示意[4],该方法的基本原理是在对汽车转弯半径R进行控制的基础上,以汽车后轴中心为控制点,从该点出发到前视距为ld的参考路径目标点(Gx,Gy),再根据阿克曼转向模型(Ackerman Turing Model),计算出所需要的前轮转动角度[1]。
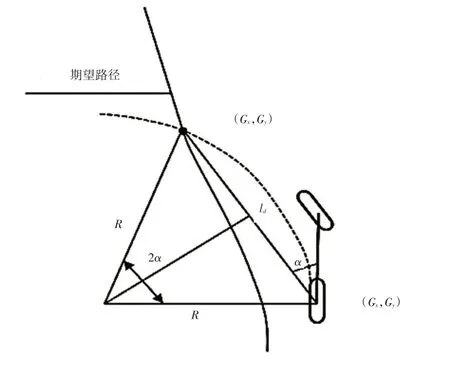
图2 纯路径跟踪模型[4]
根据几何关系:
可得车辆转向半径R和转向曲率ρ分别为:
式中,α为车辆中心平面与前视矢量的夹角;ye为侧向位移的误差。
算法可以理解为转向曲率ρ是关于侧向位移误差ye且增益系数为2/l2d的比例控制。
参考需求的转向半径R,l为车辆前后轮距离,结合阿克曼转向模型,可以计算出前轮转向角δf:
纯跟踪算法(PP)方法简便,对路面曲率扰动有较强的抗干扰能力,但其对前视点选取的依赖性较强,且最优化结果难以获得。另外,单纯的跟踪方法建立在一个简单的几何模型上,没有充分地考虑汽车动力学特征以及转向执行器的动态特征。在车速为100 km/h 行驶条件下,由于转弯曲率急剧改变容易引起汽车侧滑,且由于系统建模与真实汽车特征差异过大,跟踪效果不理想。
1.2 Stanley算法
Stanley 算法也称之为前轮反馈控制算法。Stanley 算法基本思路是根据前轮中心的路径跟踪偏差值进行计算,得到转向盘的转向控制量。Stanley 算法模型见图3。该算法以车辆前轴中心到最近参考轨迹点的距离为基础的非线性反馈函数,可以使横向跟踪误差指数收敛到零。通过汽车姿态和参考路径之间的几何关系,可以直接得到汽车转向盘的控制量。前轮转角的控制变量主要包括2个方面:

图3 Stanley运动学模型[5]
(1)航向误差形成的转角,就是期望轨迹上与车身最近点的切线方向与车辆方向的夹角。
(2)由横向误差造成的夹角,也就是在侧向偏差下,前轴车轮的中心与期望轨迹最近的点之间的夹角[5]。
在不计横向误差的前提下,汽车前轮的偏角必须与已期望路径参考点的切线方向一致。如果忽略了航向跟踪的偏差,则会使横向跟踪误差增大,从而使前轮转向角变大。
与纯跟踪算法相比,Stanley 算法的优势在于该算法同时兼顾了车辆偏航角和车辆与跟踪路径之间的横向误差,其核心思路是根据前轮的轨迹追踪偏移量来确定转向盘的转向控制量。在此基础上,提出了一种非线性反馈函数方法,该方法以车辆前轴中心与最近路径点的间距为基础,将横向跟踪误差指数收敛到零。利用汽车姿态和参考路径之间的空间位置相关性,可直接得到汽车转向轴角度的控制量。
当路径为连续可导且路径曲率变化时,Stanley 算法前轮反馈系统具有一定的局部指数收敛特性。但是可以看到,这种方法并不适合在汽车倒车的情况下使用,在像自动泊车这样需要短距离倒车的情况下也不能使用。此外,还需要有更高的期望路线的光滑平整度,在道路曲率光滑度不佳的时候,很可能会发生车辆响应超调过大的问题[6]。
1.3 比例积分(PID)算法
传统PID 控制算法发展较早,相对也更为成熟,由于PID 不需要对被控对象进行建模,而且其控制需要的参数较少,多应用于智能汽车纵向轨迹跟踪控制。此外,该算法在应用于智能汽车的横向轨迹跟踪控制时,由于单独的传统PID 控制算法已经无法满足如今多变的智能汽车参数及道路环境,无法适应高度自动驾驶汽车轨迹跟踪控制。目前纯粹的传统PID控制应用也已很少,应用更多的轨迹跟踪控制算法是和其他控制器联合实现复合控制,如Tsai 等[7]基于预测控制和输出递归模糊小波神经网络来进行在线参数学习和自适应PID 算法,Phu 等[8]利用模糊PID 来提高PID 的适用性,以PID 为基础,研究其他弥补短板的优化方向。
MARINO 等[9]提出了一种新型串级PID 横向控制方案,该方案采用外环回路,利用横向误差值间接获得所需的期望横摆角速度,内环采用比例积分(Proportional Integral,PI)控制,实现了对横摆角速度的实时追踪,并利用极点配置对控制器的参数进行调节,实现整体的渐近稳定性。然而,该算法仅根据智能汽车与路径之间的运动规律进行了线性化,不能实现较大幅度的横向位移量的递增收敛,也不能充分考虑执行器的限制因素。
北京理工大学赵熙俊等[10]提出了一种新的航向偏差反馈控制策略。分析运动学方程,获得了目标航向角误差。并在这基础上,以车与路耦合系统为基础,根据车速不同分段,提出了一种分段固定增益PID 控制算法,并通过实车实验验证了其对非结构性路面的良好跟踪性能,其横向控制系统试验结果如图4 所示。

图4 横向控制系统试验结果[10]
以上文献所提出的PID 控制方法在单一变量的情况下,能体现出较强的跟踪性能,包括速度、横摆角速度和航向角。尽管PID 控制方法简便、高效,从理论上讲,根据模型调整PID 参数能获得最佳结果。但在不知道模型或处于时变系统的情况下,调整PID 参数通常需要大量经验,且计算复杂度较高。同时,由于外界干扰和不确定因素的影响,使得难以达到大范围内的渐近稳定性。此外,常规PID 控制方法还存在着因执行器容量饱和而引起的积分操作发散现象,因此必须对其进行进一步的改进以防止积分饱和。
1.4 线性二次调节器(LQR)算法
LQR 采用全状态线性反馈控制器,构建闭环最优化控制系统,对二次优化问题进行归一化处理,给出优化结果的解析解,并在保证多个性能目标的前提下,进行优化设计,可以较好地完成对目标路径的最优跟踪控制,因此常被用于智能汽车横向运动控制中[11]。
徐明泽等[12]和张栩源等[13]都提出了融合LQR 和PID 算法,前者采用遗传算法对横向LQR 控制的关键参数进行了确定,后者提出了前轮转角补偿控制,都能提高智能汽车轨迹跟踪的精度及鲁棒性。
Snider[6]简要阐述了LQR 在轨迹跟踪方面的应用。采用汽车质心为控制点,对含有路面弯曲干扰的汽车进行建模,采用不考虑干扰项的线性二次型调节器,虽能保证系统的稳定性,但因干扰项的存在,其稳态误差依然存在。针对这一问题,又提出了一种在LQR 反馈控制的基础上增加道路曲率前馈环节的控制方法,以减小横向位移的稳定误差。但因为控制点在质心位置的预瞄距离为零,所以前馈信号只有被动响应,超调比较明显,而预瞄信号的加入可以提高控制效果。
二次调节控制器在多目标跟踪控制的表现良好,徐明泽等[12]和张栩源等[13]结合PID 算法进行横向控制,能发挥出2 种算法的优点。但LQR 结合PID 算法缺点也很明显,即在整个过程中都进行了线性化处理,将环境干扰和路面情况理想化,在乡村道路或人流量较大的胡同环境下不稳定性大大增加,需要制定合理的优化方法或者引入新的算法结合,降低外界干扰带来的影响。
1.5 模型预测控制(MPC)
由于智能汽车所面对的是一个不断发生变化的复杂环境,必须要符合关键安全约束和执行器约束条件。而MPC算法可以对预测信息进行全面分析,对多约束优化有着很强的处理能力。同时,其在理论与计算方面的同步发展,拓展了实时MPC的适用领域。传统MPC 已经较为成熟,如今更多的还是对MPC 算法进行改进,如基于参数自适应、变步长、时域自适应等的AMPC 算法,如基于多控制器、引入其他智能算法的蚁群算法、神经网络算法和遗传算法等。为此,研究人员在模型预测控制技术的基础上进行了大量的算法研究。Mata 等[14]提出了一种以多重约束为基础的最优轨迹跟踪控制策略,该策略采用了连续线性化误差模型,并采用二次规划求解MPC,从而实现了较好的轨迹跟踪精度。基于该方法,Son 等[15]提出了一种面向倒车行驶的转向控制方法,该方法具有比斯坦利(Stanley)方法更强的鲁棒性和更高的追踪准确率。
李伯雄等[16]提出一种将扩展卡尔曼滤波法与模型预测控制法结合的控制算法,模型结构如图5所示。试验采用3种不同的路面附着系数来模拟路面附着情况,用于实现车辆横向轨迹跟踪,以保证智能汽车在未知路面工况下的行驶安全,使智能汽车跟随预期轨迹行驶,有效提高了智能汽车在不同附着系数路面行驶时横向轨迹跟踪的稳定性及鲁棒性。

图5 横向跟踪控制算法模型[16]
赵树恩等[17]针对下智能汽车轨迹跟踪的精确性和车辆行驶稳定性等要求,提出一种基于扩张状态观测器(Extended State Observer,ESO)的MPC 策略,利用ESO 对车辆状态时变特性、道路环境不确定性因素引起的干扰进行在线估计,从而提高智能汽车在弯道且存在干扰环境下进行轨迹跟踪的鲁棒性和实时性。
相比较前面的PID 和LQR 轨迹跟踪算法,MPC算法在处理多约束问题上有更大的优势,在处理外界干扰和路面附着问题方面,跟踪算法精度更高,鲁棒性更好。但在实际应用过程中运算复杂,多约束处理时存在冲突,无法找到最优解,成本也高。
1.6 其他算法
由于滑模控制(Sliding Mode Control,SMC)对参数变化及扰动不敏感,系统具有极强的鲁棒性且当其应用于非线性系统时,无须进行复杂的线性化,能更便捷稳定地实现控制,也常应用于轨迹跟踪,如王俊昌等[18]基于快速幂次趋近律设计智能汽车轨迹跟踪SMC,通过智能汽车自主转向控制跟踪参考轨迹,通过横摆力矩控制跟踪参考横摆角速度。此外,利用横摆力矩控制量设计了前轮转向角补偿模块,通过轨迹跟踪和横摆稳定控制器的协调,进一步修正轨迹跟踪精度。
李鹤年等[19]基于遗传算法整定滑模参数、马瑞梓等[20]基于神经网络实现滑模变结构来提高控制精度和效果。Aslam 等[21]利用模糊滑模控制来对滑移转向智能汽车进行轨迹跟踪控制。
滑模控制和改进型自抗干扰控制算法本身在提高智能汽车操控性能、安全性和适应多样路况方面有显著优势。在此基础上使用快速幂次律、遗传算法、神经网络方法提高跟踪精度。滑模控制器由于成本高、耗能大和维护频繁的问题限制了其使用范围。表2总结了轨迹跟踪算法优缺点。
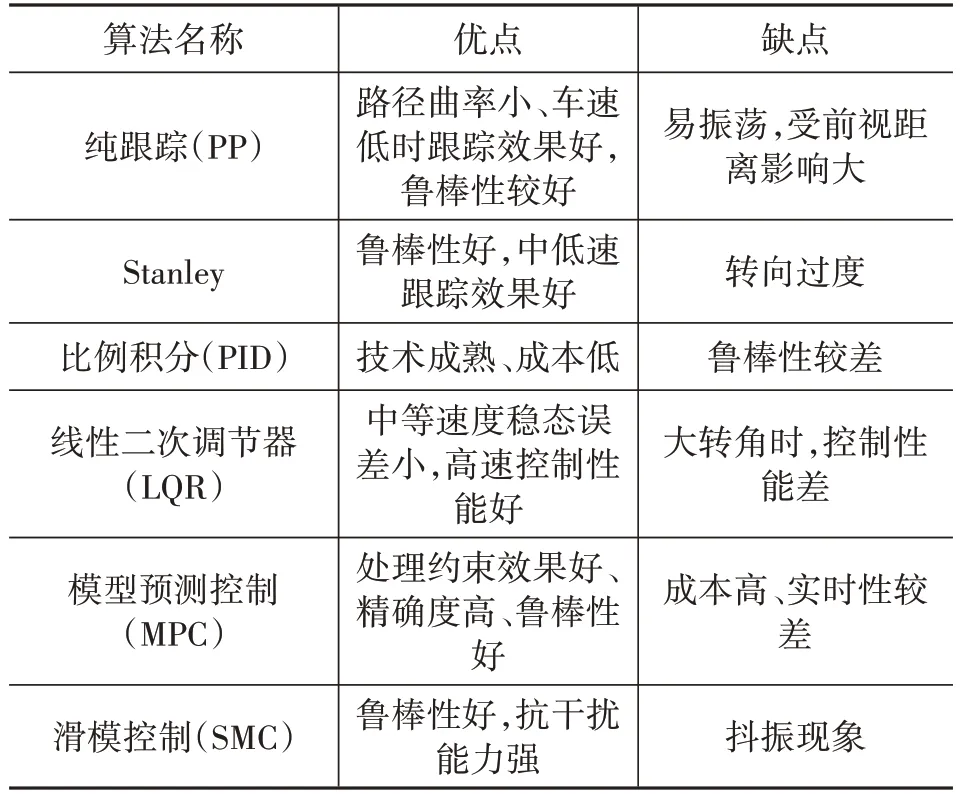
表2 轨迹跟踪控制算法优缺点
2 轨迹跟踪算法优化
传统轨迹跟踪控制算法大多只能适用于智能汽车中低速工况,高速工况下可能会失稳,精度有所降低。为提高智能汽车轨迹跟踪精度,通常会采用以下方法对轨迹跟踪算法进行优化。
2.1 卡尔曼滤波
周云等[23]针对基于压缩感知技术的目标跟踪算法存在的跟踪漂移问题,提出了一种采用改进压缩感知算法和卡尔曼滤波(Kalman Filter,KF)方法相结合的车辆目标跟踪算法,通过KF 增益系数对预测值与观测值进行修正,获得最终目标跟踪结果。最后,在修正后的目标区域周围进行正负样本采样,以实现朴素贝叶斯分类器更新,进而实现目标跟踪轨迹的实时更新。
于晨等[24]基于扩展卡尔曼滤波算法(Extended Kalman Filter,EKF)融合惯性传感器、地磁传感器与编码器数据,解决轮式移动机器人在实际轨迹跟踪任务中存在传感器测量误差且测量噪声统计信息获取困难的问题。
陈莹等[25]利用平方根卡尔曼滤波(Unscented Kalman Filter,UKF)提出了一种多传感器融合跟踪方法,以协方差平方根阵代替协方差阵参加迭代运算,可有效抑制滤波后的误差,提高系统的跟踪准确率。
卡尔曼滤波是比较成熟的状态估计算法,应用在智能汽车轨迹跟踪中,能很好地提高实时性和精确性,针对模型要求高和噪音测量误差问题,可以使用扩展卡尔曼滤波和粒子滤波方法进行改进。
2.2 粒子滤波
Jia 等[26]提出了一种基于粒子滤波(Particle Filter,PF)的自适应强跟踪粒子滤波算法。根据每时刻实际测量值和预测测量值之间的残差,通过特定算法流程,自适应地对遗忘因子和弱化因子进行调整,来提高跟踪精度。
Lin 等[27]提出了一种改进的基于PF 的跟踪算法,将所有颗粒分为2部分并分开放置。第一次放置的粒子数量足够大,以确保可以覆盖目标的粒子数量尽可能多,然后将第二部分粒子放置在与第一次放置粒子中的模板最高相似度的粒子位置,以提高跟踪精度,在复杂场景下的鲁棒性,并解决由快速移动目标引起的漂移问题。
粒子滤波性能与粒子数目有关,过多和过少粒子数目都会影响测试结果,Lin 等[27]提出了分步放置的方式解决了粒子滤波的估计结果不准确和复杂度高的问题。此外粒子滤波还存在采样偏差和粒子退化的问题,Jia等[26]对遗忘因子和弱化因子进行调整。除了上述方法外还可以通过基于树结构、基于网格方法对粒子滤波优化方法进行完善。
2.3 强化学习
增强学习是一种通过学习从状态到行为进行匹配来获得最大收益的一种学习机制。这学习机制必须在外界条件下持续试验,并根据外界条件(激励),持续地进行状态-行为优化对应关系。反复试验(Trial and error)和延时奖励(Delayed reward)是强化学习中的2 个主要特点。将其用于车辆跟踪,其背景包括车辆模型、跟踪模型、路面模型以及回报函数。
贺伊琳等[28]在此基础上,利用强化学习的深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法,在目标跟踪过程中,根据目标的横向偏差、角度偏差以及路径曲率,判断目标的转向角,进而完成目标的自动追踪,并进一步提升追踪准确度。
夏家伟等[29]提出一种基于近端策略优化的深度强化学习轨迹跟踪控制算法,生成轨迹任务数据集来模拟复杂的任务环境,以此作为深度强化学习控制器的训练样本输入,增强控制器的鲁棒性。
强化学习能在无模型情况下,机器学习驾驶数据是一种模仿人类驾驶的方式。在上述文献中可以看出强化学习提高了目标跟踪的精确性和智能化程度。与传统的控制算法结合,能实现更高级的轨迹跟踪效果,但需要在训练时间和样本效率方面做出更有效的改进。
2.4 深度学习
如Vaquero 等[30]利用卷积神经网络(Convolutional Neural Network,CNN)来对图像序列进行处理,可以有效地提取特征并预测物体的运动轨迹。
金辉等[31]提出了一种利用前馈神经网络对所处路段进行路面附着系数辨识的新算法,并提出了一种多参数的预测控制轨道追踪算法,从而在确保跟踪准确率和行驶平顺性的前提下,进一步提升了其运算效率。
李志坚等[32]结合高速公路监控视频,设计了高效的CG3 瓶颈层结构来优化Yolov5 目标检测算法,并利用改进了损失函数的Deepsort多目标追踪算法进行车辆轨迹检测与跟踪,优化后的算法得出的车辆检测精度由92.8%提高到了96.3%,精度提高了3.5%。
肖宗鑫[33]等基于径向基神经网络的自适应补偿和鲁棒控制设计了优化后的MPC轨迹跟踪控制系统,减轻智能汽车侧滑程度,提高智能汽车行驶稳定性。
相比于强化学习,深度学习在数据驱动学习、特征学习和表征能力、高级模式识别方面更有优势,同时也存在数据需求量大和解释性差的缺点,可以结合强化学习、可视化、注意力机制(Attention Mechanism)技术来改善。
2.5 迭代学习控制
对于具有重复运行这种特质的系统,采用迭代式学习控制,根据已有动作的误差信息,对当前动作的输入信号进行修正,从而实现对已有动作的最优控制。
裴九芳等[34]采用了迭代学习控制(Iterative Learning Control, ILC)来对所述移动机器人运动轨迹进行控制和跟踪。
卜旭辉等[35]利用ILC 理论对农机作业车的行驶轨迹进行了分析,利用压缩映射法对其进行了收敛分析。
姚文龙等[36]将时变、非线性因素纳入到一个迭代域下全格式动态线性化数据模型,并在此基础上,利用时间差分的思想,研究一种新的、具有最优特性的、无需建模的自适应迭代控制方法,有效提升了轨迹跟踪的准确性与鲁棒性。
由于迭代学习控制能适应非线性系统,有较小的模型依耐性。很多学者将其应用在轨迹跟踪方面,需要注意的是要对其初始化进行合理选择,以满足其收敛性较高的要求。
2.6 其他优化方法
除以上优化方向外,其他如多控制组合优化算法、粒子群优化算法、遗传优化算法等也有应用。例如吕文杰等[37]利用了模糊控制(Fuzzy Control,FC)的思路和纯跟踪的算法,将智能汽车行驶速度和航向偏角作为模糊控制器输入,以此将前视距进行合理动态调整。相对于固定前视距离的纯跟踪算法,该方法可以显著地改善目标的跟踪性能。
王鑫等[38]将PP 算法与Stanley 算法结合,对车轮转角的计算方式进行改进,根据智能汽车航向角、横向偏差、车速特性,基于合适的预瞄距离,实时计算智能汽车在当前车速下合适的车轮转角,更好地满足智能汽车跟踪精确度和平滑性要求。
唐传茵等[39]提出了一种可以调节参数的基于PSO算法的模型预测控制器,结合轮胎的动力学特性及智能汽车动态特性对轮胎侧偏角、质心侧偏角进行约束来提高智能汽车在高速下的路径跟踪效果。
苑风霞等[40]在遗传算法的基础上,引入了衰减速率先慢后快的高斯衰减函数,使其能够合理分配预测量和控制量的权重,证实了这样的策略对目标轨迹跟踪精度效果显著。
不同算法和调节参数方法引入,都是为了跟踪的效果又快又稳,满足乘坐安全性、平稳性和舒适行要求。要特别强调外界干扰、道路附着系数变化和动态场景下的实时性和精确度。随着技术不断突破,轨迹跟踪控制的效果也不断增强,多算法融合已经成为一种新趋势。
3 结论与展望
本文综述了智能车辆轨迹跟踪控制的相关研究。从几何运动学、运动学和动力学建模分类出发,对相关轨迹跟踪算法以及它们的优化方向进行了探讨。分析总结得到以下结论和展望:
(1)当前,智能车辆的轨迹跟踪研究并不满足于中低速车速的单一控制算法,需要多方向、多层次深入研究,纵向发展单一算法的延伸方向弥补原有不足,横向结合其他智能优化算法或者将多种轨迹跟踪算法结合来提高其控制精度和操纵稳定性。
(2)在智能化不断发展的时代,深度学习、强化学习凸显智能化算法与智能汽车轨迹跟踪控制联系会不断加深,应当拓展智能算法在轨迹跟踪上的应用场景。
(3)当前,轨迹跟踪应用场景简单,参考轨迹也大多较简单,轨迹跟踪控制算法很少得到应用于一些极端条件的场景上。在此基础上,针对城区、山区的复杂路况,充分利用实时感知和预报信息,开展基于不确定因素的智能汽车运动轨迹跟踪与控制方法研究。

