气流清扫的超音速喷管气动设计及其性能的对比分析

赵宏星，卢耀辉，王北昆，唐波，罗银生，陈德君，毛荣生

（1.西南交通大学 机械工程学院，成都 610031；2.唐山百川智能机器股份有限公司，河北 唐山 063000）

轨道车辆的制动力通过轮轨间黏着进行传递，轨道干燥时，黏着力足以为车辆提供制动力[1]，但特定环境下，潮湿的空气和较大的温差会使轨道表面被露水覆盖，导致制动力不足，影响运营[2-3]。高速气流在水膜表面可以产生拖曳力对其进行吹除，已用于灰尘和雪的清扫[4-5]，但用于水膜清扫的研究还未出现，因此提出使用拉瓦尔喷管产生超音速射流来清扫表面水膜。

清扫过程本质为水膜在高速气流剪切作用下的流动和破碎。雨水在飞机表面的流动与此过程类似[6]，其使用韦伯数作为高速气流作用下水膜的吹离判据。超音速气流产生的关键是拉瓦尔喷管气动设计。考虑到压缩机的性能限制，工业喷管尺寸在毫米尺度。微型设备的加工更难[7]，中心轴对称喷管性能更优，但对于微型制造难度更大，所以小尺寸喷管更倾向于使用2D喷管[8-9]。毫米级2D喷管的扩张角、雷诺数和深度对性能的影响也不相同[10]。型线也是影响喷管工作性能的重要因素[11]，其中，锥形型线在微喷管中最为常用[7]。型线设计中，常使用特征线法使壁面可以消波，从而提高喷管性能。其中，Sivell法多用于风洞，可以产生均匀实验段流场，微型喷管则普遍使用短化喷管设计方法[12]。

拉瓦尔喷管的水膜清扫能力取决于与水膜接触的外流场，需要对喷管内外流场的准确预测。微型超音速喷管的微型尺度导致黏性损耗过大而影响流场[13]。Cai等[8]和Meng等[9]分别对规律和随机的加工表面进行详细建模，并使用Sutherland模型来表征其黏性，通过实验验证了这种方法。清扫发生在喷管外，需要气流在出口外一段距离仍具有相当的动能。Zhao等[14]使用仿真和实验的方法对不同喷管外流场的衰减进行了研究，这对清扫性能的研究是必要的。喷管流场的仿真此前多对雷诺平均方程（RANS）进行求解，但这种方法无法表示湍流的各向异性。Quaatz等[15]基于大涡模拟（LES）对喷管的外流场进行了预测，LES方法仿真得到的激波结构与实验一致。

本文设计了不同的气流清扫拉瓦尔喷管，并进行流场和清扫性能的比较研究。分别设计了中心轴对称锥形喷管、中心轴对称Sivell法喷管、中心轴对称短化喷管和二维锥形型线喷管，基于LES方法建立了包括外流场的喷管流场数值仿真模型，并进行了仿真。基于仿真结果，研究了几种喷管的内外流场结构。分析了几种喷管外流场的水膜清扫性能差异，得到用于水膜清扫的最优喷管类型。

1 拉瓦尔喷管设计

1.1 气流清扫的性能要求

水膜的清扫过程如图1所示，高速气流到到达水膜时产生拖曳力，对水膜的做功为：

图1 超音速气流清扫水膜Fig.1 Water film removal process by supersonic air flow

式中：Wa为黏附功；ρa为来流气体密度；H为液膜高度；s为气流与液膜接触面积。水滴与固体表面的相互作用用黏附功计算：

式中：σlv为表面张力系数；θ为接触角。由于重力作用可以忽略[6]，因此当气体拖曳力做功大于黏附功时液滴破碎，水膜中破碎的部分随气流被吹离，黏附功与拖曳力做功为：

水膜的接触角受很多因素影响，分析中使用完全浸润的水膜作为标准水膜，接触角θ=0°，温度为25 ℃，其表面张力系数为71.97 mN/m。因此可以得到标准水膜在高速气流清扫后的厚度：

式中：Hw,cr为标准水膜清扫后理论上的剩余厚度[6]，并非任何表面的水膜在吹除后的厚度，实际清扫后的水膜厚度与水膜的状态和轨道状态等因素有关。气流的Hw,cr更低意味着同一水膜清扫后厚度更低，所以将其作为与水膜条件无关的气流清扫性能评价参数，称为等效水膜厚度。

1.2 拉瓦尔喷管的基本原理

拉瓦尔喷管由收缩段、喉部和扩张段组成。将其过程视为绝热等熵过程，理论上每个位置的马赫数与其所在的位置横截面面积A有关[16]，如式（6）所示。

式中：A1为喉部面积；k为比热比。设计工作状态完全膨胀，质量流量qm如式（7）所示。

式中：p0为入口气流的迟滞压力；T0为入口气流的温度；Rg为气体常数。根据压气机性能确定喷管的主要参数：入口迟滞压力p0=1.6 MPa；入口迟滞温度T0=573 K；出口马赫数Ma2=2.45；喉部面积A1=18.92 mm2；出口面积A2=47.72 mm2；流量qm=0.051 1 kg/s；Hw,2=0.169 μm。

1.3 拉瓦尔喷管的流道设计

微型喷管中常用的2种几何型面为中心轴对称和二维轴对称。型线设计方法众多，其中最普遍和简单的是锥形型线。本文分别设计了中心轴对称锥形型线喷管和二维轴对称锥形型线喷管，中心轴对称喷管锥形型线的半扩张角定为7.7°。二维锥形喷管性能由高宽比和半膨胀角决定，根据研究，选择出口的高宽比为0.4，半膨胀角为15°，以达到此结构下最优的喷管性能[10]。

型线分为收缩段和扩张段型线设计。收缩段型线对性能的影响较小，选择五次方曲线法[17]。特征线法（MOC）喷管设计方法是对喷管内流场较优的方法。经典MOC方法之一的Sivells法可以产生较为均匀的流场，但长度较长，制造难度较大，且会加剧附面层效应[18]。同样基于MOC的MLN法可以缩短喷管长度[19]，其中采用直音速线的SSL-MLN法的短化效果最好，可以减小附面层带来的性能劣化。

Sivell方法基于特征线理论，通过喷管的型线设计使激波在壁面上不断反射，从而在出口形成轴向射流[18]。假设扩张段存在4个区域，从喉部进入初始膨胀区（图2a①）。随后进入源流区，在其中，流体流动角从轴线到壁面均匀发散。经过后续区域（图2a②和③）壁面的反射后方向逐渐转变至轴线方向，进入均匀流区域，直至出口处气流方向都垂直于出口截面。特征线网格求解从源流区开始，气流的流动角从核心区0°逐步增加至最大流动角，通过特征线方程求解得到特征线网格，最后通过流量积分法在特征网格上截取得到的型线如图2a所示。

图2 型线设计Fig.2 Profile of Sivell nozzle

SSL-MLN中的SSL指假设喉部存在直线的音速线，然后经过初始膨胀和消波曲线后直接达到设计马赫数，采用这种方法可使喷管的扩张段缩短50%[19]。其在喉部进行初始膨胀，而后膨胀波从轴对称线处反射，与假设的音速线包围形成一个为非简单波的核心区，而其与扩张段壁面之间的过渡区也是一个非简单波区。2个区域都需要数值方法进行求解，根据音速线和中心轴对称线等边界理想参数与膨胀波的变化，并基于MOC方程，可以逐个求解2个区域内离散后的特征线网格。特征网格结果如图2b所示，图2b ①区为核心区特征线网格，图2b ②区为过渡区特征线网格。壁面根据壁面斜率与流动角关系方程确定，使用欧拉预测修正方案迭代求解[19]。

2 数值模型的建立

2.1 数值模型

毫米级喷管需注意气体的连续性，其可用努森数（Kn=l/L）即分子气体平均自由程l和设备特征尺度L之比评价，小于0.001的流场满足连续性流体假设[20]。微型喷管内表面积与流道体积之比更高，不同区域的黏性差异对流场的影响明显，选择Sutherland 方程描述黏性随温度的变化[8]。

微喷管的超音速流场雷诺数较高，这种自然非稳态湍流会受到强烈的非均匀性效应和快速变化的影响，大涡模拟（LES）将N-S方程进行滤波后的方程进行求解，在时间上是非均匀的，可以用于非稳态湍流流场量（大尺度涡）的直接求解[21]。选择经过实验验证的WMLES模型[22]进行SGS建模，处理大尺度上发生的不能在既定网格上进行计算的小尺度重要物理过程。

仿真使用压力入口出口，壁面绝热。采用二阶迎风差分对各个方程进行离散，使用Fluent的密度基隐式耦合双精度求解器。每个时间步通过对流场的几个方程残差进行控制，所有方程的残差小于1×10–5时为收敛[11]。LES使用隐式求解器时CFL需要在5～50，使用恒定边界条件调整时间步长，使流场可以进入稳态，或者稳定波动时取其平均值所在的时间步结果。

流场从出口处开始分别沿轴向和径向扩展10R2和5R2研究外流场特征[23]。设计的喷管参数见表1，结构如图3所示。Ld为扩张段长度，MLN-A相比Taper-A扩张段可以缩短50%以上。

表1 喷管的主要参数及其边界条件Tab.1 Key parameters and boundary conditions of nozzles

图3 不同喷管结构Fig.3 Structures of different nozzles

将网格划分为结构化网格为主的3-D网格，壁面进行加密，使边界层准确地预测。y+小于1.5[24-25]，选择Kamali的网格尺寸作为射流核心区域的尺寸约为0.3 mm，网格规模约2×106[26]。

2.2 模型验证

采用与Zhang相同的参数和MLN法设计得到一致的喷管，建立基于LES的数值模型，使用相同的边界条件进行仿真，结果与实验结果对比如图4所示[27]。将密度梯度进行处理与实验的纹影图进行对比发现，LES结果在中心轴向周围的衰减和马赫环的位置准确度较高，基本与实验结果一致。Kn数最大为6.42×10–5s，远小于0.001，连续性假设成立。

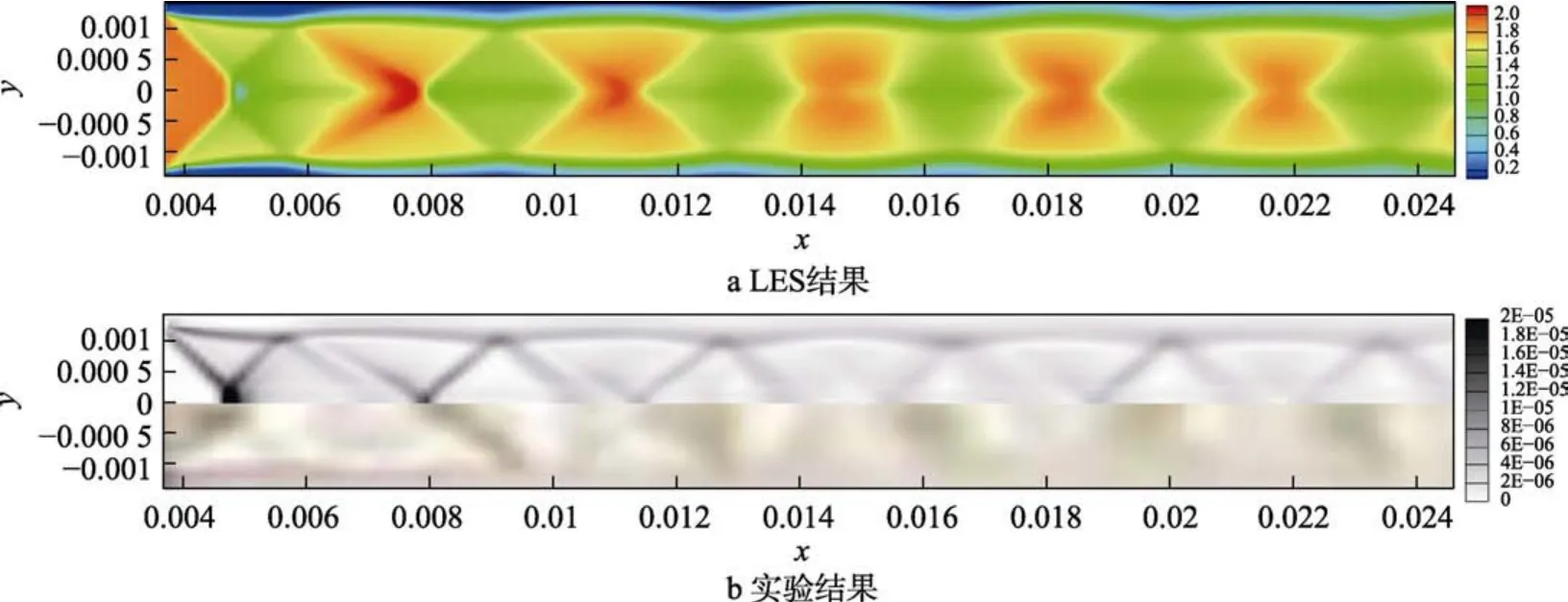
图4 仿真结果验证Fig.4 Verification of simulation results: a) LES results; b) experiment results

3 结果与讨论

马赫数在纵截面上的流场结构如图5所示。沿轴线和出口径向上马赫数的变化如图6所示。为方便比较对扩张段和外流场分别进行无量纲化处理，无量纲化坐标xL的–1～0为扩张段流场，0～4为外流场，出口径向无量纲化坐标yL从0到1为从中心轴线到壁面。

图5 不同类型拉瓦尔喷管的流场结构Fig.5 Flow field of different kinds of nozzles: a) Taper-A;b) Sivell-A; c) MLN-A; d) Taper-2D

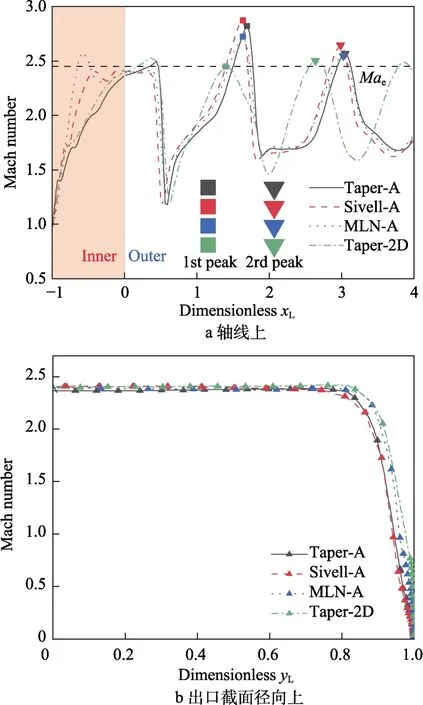
图6 不同结构喷管的马赫数Fig.6 Mach number of different nozzles: a) Mach number on the axis; b) Mach number on the radial direction of the outlet section

从图6a可知，气流的从喉部的音速开始加速，其中2种锥形型线喷管（Taper-A和Taper-2D）的马赫数变化类似，都以相对稳定的速度提升直到出口处。MOC喷管（MLN-A和Sivell-A）都是从扩张段开始快速提高，由于MLN-A喷管从扩张段初始段就以较大的扩张角膨胀，所以气流快速加速至设计马赫数，而后经过壁面的反射消波，到出口处接近设计马赫数。Sivell-A喷管的马赫数提升更加平稳，在整个收敛-扩张段的膨胀角都是更为连续的，出口处马赫数最高。Taper-A型喷管的出口马赫数最低。同时可以看出，喷管沿轴线的马赫数波动下降，其中3种中心轴对称喷管的波动特征类似，其达到波峰的顺序为Sivell-A、MLN-A和Taper-A，同时其波动幅值变化趋势恰好相反。这是因为过大的波动幅值会导致更多的能量耗散，马赫数进入波动下降阶段的2个波峰如图6a所示。

从图6b可以看出，Sivell-A喷管沿径向上的速度衰减相对较大，原因为气流通过喷管口后，迅速膨胀加速到设计马赫数，随着喷管长度的增加，附面层累计加厚，从而导致流速衰减变大。Taper-A喷管虽然也较长，但在接近出口的位置才膨胀充分，且马赫数较低，所以衰减次于Sivell-A喷管。Taper-2D喷管都在出口处才逐渐膨胀至设计状态，虽然喷管内壁面积与扩张段容积之比较其他喷管具有明显劣势，但附面层累计的效应相对更弱，最终导致其出口马赫数衰减情况更轻。MLN-A较短的长度使得在膨胀较为充分的情况下出口截面附面层也与Taper-2D喷管相当，优于其他2个喷管。

外流场线轴线上射流的剩余水膜厚度Hw,cr如图7所示。轴线上Hw,cr为马赫数的变化相似的波动状态。将MLN-A喷管射流在轴线上的速度、密度和Hw,cr变化趋势进行比较，结果如图8所示。可以发现，Hw,cr的波峰、速度波峰与密度波谷位置相同。Hw,cr与密度和速度平方分别成反比，速度波动幅度变化不大，而密度波动在峰值时约为出口处的4倍，因此在此设计参数下，Hw,cr主要受密度波动变化影响，密度波峰与Hw,cr波谷同一位置。

图7 等效水膜厚度沿中线轴线的变化Fig.7 Variation of equivalent water thickness along the centerline axis

图8 等效水膜厚度、速度和密度沿中线轴线的变化Fig.8 Variation of equivalent water thickness, velocity and density along the centerline axis

喷管在实际清扫时，气源的稳定性和喷管本身的振动会导致喷管位置和流场结构发生变化，因此要求实际清扫xL>2区域轴线上的Hw,cr最大值Hw,cr,max<0.2 μm。不同喷管类型的Hw,cr按Sivell-A、Taper-A、MLN-A和Taper-2D的顺序递减，代表其清扫性能变化相反。xL>2范围Hw,cr<0.2 μm的喷管有MLN-A和Taper-2D。

对在第二个马赫数波峰截面上的Hw,cr分别进行处理，得到Hw,cr<0.2 μm的区域面积，即有效清扫面积A0.2，以及各个喷管的A0.2与喷管1之比，见表2。可以看出，MLN-A喷管的A0.2最大，约为Taper-A的105%，更比Taper-2D喷管大15%，有效清扫面积最大。

表2 第二个波峰截面有效清扫面积Tab.2 Flow field structure of the second wave crest section

有效清扫面积内的Hw,cr沿径向的变化如图9所示。Taper-A和Sivell-A喷管在远离轴线的部分等效水膜厚度也有相当部分小于0.2 μm，但整体依然大于MLN-A和Taper-2D。同时MLN-A喷管的整体Hw,cr更小，也更均匀。Taper-2D的有效清扫面积形状与中心轴对称喷管不同，其与MLN-A喷管的有效清扫面积如图10所示，在使用中需要单独考虑。

图9 等效水膜厚度在第二个波峰截面沿径向的变化Fig.9 Radial variation of equivalent water thickness at the second wave crest section

图10 等效水膜厚度在第二个波峰截面的分布Fig.10 Distribution of equivalent water thickness on the second wave crest section

4 结论

1）通过清扫过程的动力学分析，得到基于韦伯数的吹离的判断方法和水膜清扫性能评价指标等效水膜厚度Hw,cr。

2）超音速气流进入外流场后速度呈波动衰减，喷管长度会加剧附面层。MOC喷管即MLN-A和Sivell-A的流场膨胀更充分，但MLN-A较短的长度使其附面层效应的影响更小，在速度波动中能量耗散最少。

3）喷管长度对性能影响较大，MLN-A和Taper-2D轴线上的清扫性能波动幅值更小，在xL>2区域的最大等效水膜厚度小于0.2 μm。MLN-A有效清扫面积比Taper-2D的喷管高15%以上，清扫性能最优。