基于移动边缘云的计算密集型任务卸载决策算法

王志强 王金婉

(济源职业技术学院信息工程系 河南 济源 459000) 2(南京大学信息管理学院 江苏 南京 210023)

0 引 言

随着物联网和可穿戴设备等移动技术的迅速兴起,智能移动设备的使用正变得越来越广泛,它为支持新型的移动应用提供了有力平台,在交互型游戏、人脸识别、自然语言处理等领域得到了广泛应用[1-2]。这种计算密集型应用比移动设备上执行的传统型应用需要更加强大的计算能力和消耗更多的能耗[3]。而通常移动设备拥有受限的计算资源(CPU频率和内存有限)和电池容量,这种移动应用的有效执行给移动设备带来了巨大挑战[4]。

由于边缘云服务器拥有比移动设备更加强大的计算能力,移动边缘云可以利用移动设备至云端服务器间的任务迁移解决移动设备上执行新型应用任务的效率问题,即计算卸载技术[5]。然而,云服务器通常距离移动设备较远,这样会导致较高的传输延时,不利于延时敏感型应用。移动边缘云作为一种新的计算模式[6-7],通过5G网络极大地拉近了云计算资源与移动设备间的距离,比较传统云计算,移动边缘云以计算卸载提供了更低的延时和计算灵活性。然而,考虑到经济性和扩展性问题,移动边缘计算服务器的计算能力通常较为有限,此外,密集型网络中的计算卸载可能导致更多的干扰和传输延时[8]。因此,将所有计算任务卸载到移动边缘计算服务器上执行显得不切实际,部分应用仍需在移动设备本地上执行。本地执行虽然能耗更高,但此时不存在额外的通信或等待延时。综合考虑,做出合理的任务卸载决策,是提高本地应用任务执行效率的关键问题。

任务卸载决策问题是移动边缘云中需要处理的关键问题,主要体现在:第一,卸载决策过程会随着任务数量的增加而呈指数级增长,利用穷尽搜索机制显然不切实际;第二,通用任务图结构(顺序任务结构和并行任务结构混合)的完成时间难以计算。此时的完成时间取决于多个客观因素,包括:移动设备端和边缘云端的并行性、边缘云端的负载状况、边缘云端与移动设备端间的通信带宽。

1 相关工作分析

移动边缘云中的任务卸载决策已有许多相关研究工作,优化目标各有不同,如移动设备端的能量优化问题、移动数据流应用的吞吐量优化问题、最为常见的计算密集型应用任务的完成时间优化问题。文献[9]设计了一种克隆云CloneCloud模型,该模型在给定的网络传输速率和设备计算能力的基础上可以利用离线算法计算应用的卸载决策。但由于作为离线算法使得寻优复杂度过高。文献[10]提出的MAUI模型可以实时地进行应用卸载决策,将卸载决策问题形式化为0-1线性规划问题,但求解整数规划的过高计算代价使得它并不适用于边缘云端的任务卸载问题。文献[11]设计的ODE算法本文研究有些类似,利用贪婪机制对通用的任务图中的任务卸载决策进行了求解。然而,该算法求解速度虽然较快,但在网络带宽受限较多时,其卸载决策解距离理论最优解相差较远,其执行效率较差。文献[12]提出了具有线性时间复杂度的近似最优卸载决策算法,然而,算法仅能够对连续的任务结构应用进行卸载决策求解,并没有考虑更为常规的并行任务结构的卸载决策问题,应用于计算密集型应用中的卸载决策表现较差。文献[13]提出了可用于通用任务结构的卸载决策算法,可以实现最大化的系统吞吐量,但是,该算法中所考虑的云端服务时间模型不切实际,不适用于实际环境。

本文提出一种计算密集型应用任务的卸载决策算法,可以实现移动设备端应用的完成时间最小化。算法考虑了更为普遍的任务结构类型,包含了顺序任务结构和并发任务结构。算法设计的出发点在于:(1) 若一个任务卸载执行,则较大可能其邻居任务也会卸载执行;(2) 应用的执行时间可以通过将任务卸载至边缘云端最大化边缘云端与移动设备端的并行性来降低任务完成时间。对于顺序任务构成的线性拓扑任务图,算法可以找到最优的卸载任务;而对于并发任务的通用拓扑任务图,算法可以最大化并行程度的同时实现任务卸载的更好负载均衡。

2 系统模型

将应用任务建模为有向任务图G(V,E),其中:V代表图的节点集,表示任务;E代表图的有向边集合,表示任务间的执行顺序约束。每个任务i∈V拥有一个权重si,表示任务i的执行指令数。有向边(i,j)∈E代表任务i与任务j间的数据传输。此时,任务i可视为父任务,任务j可视为子任务。如果一个任务拥有多个子任务,则称该任务为分叉任务(fork task),如果一个任务拥有多个父任务,则称该任务为合并任务(merging task)。每条边(i,j)拥有一个权重di,j,代表任务i至任务j间的数据传输量。

假设移动设备拥有单个CPU,其处理能力为μm。移动设备的无线设备可与自身CPU内核并行工作,CPU在进行任务计算过程中可与远程边缘云端间并行进行数据传输。若任务在移动设备上执行,则任务i的执行时间可表示为:

(1)

假设边缘云处理能力为μc。边缘云计算能力远大于本地移动设备处理能力,并且可以在多个提交应用的用户间共享,不同任务的卸载决策取决于当前边缘云负载状况。令Q表示当前边缘云端服务器上排队的任务集合,新到达任务的总排队时间为:

(2)

若任务i卸载至边缘云端执行,则其执行时间为:

(3)

需要注意的是,ci不包括任务的排队时间。若将任务卸载至边缘云端执行,在移动设备上该任务的父任务的数据传输则需要通过网络数据传输,同样地,边缘云端的执行任务也需要将数据传输至移动设备端上执行的子任务。令R表示移动设备与边缘云端间的无线数据通信速率。给定任务i与任务j的连接链路,如果一个任务在移动设备端执行,一个任务卸载至边缘云端执行,则链路的数据传输时间为:

(4)

本文的目标是将一个应用的部分任务卸载至边缘云端执行,从而降低应用的完成时间,提高应用执行效率。即给定应用的任务图结构G(V,E),算法需要寻找卸载至边缘云的任务集合,并实现应用执行时间的最小化。

3 任务卸载方法设计

目前的任务图主要有两种任务结构:顺序任务结构和并发任务结构。对于顺序任务,由于边缘云端拥有比移动设备端更强大的处理能力,因此将任务卸载至边缘云端执行可以大大降低应用完成时间。对于并发任务,除了需要充分利用边缘云端处理能力,还需要利用移动设备端与边缘云端的并行处理能力。以下就两种任务类型的卸载决策分别作出讨论。

3.1 顺序任务卸载

为了降低顺序任务的完成时间,可以尽可能将任务卸载至边缘云端执行以利用更强大的云端服务器处理能力。然而,此时的任务卸载会导致网络数据传输时间增加,该时间需要小于卸载任务节省的时间,这样才可以最终降低应用任务的完成时间。在某些情形中,网络传输数据的时间可能高于任务在本地移动设备端执行的时间。研究表明,顺序任务图的最优卸载任务集合应为任务图中连续任务序列。以图1的任务图为例,若部分任务需要卸载至边缘云端以降低任务完成时间,则任务必须是连续相邻的,如图1中的任务j至任务k。

图1 顺序任务

对于线性拓扑结构的n个任务序列,假设第一任务和最后一个任务在本地移动设备端执行,从任务j(入口任务)至任务k(出口任务)被卸载至边缘云端执行。给定入口任务j和出口任务k,其完成时间可计算为:

(5)

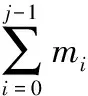
算法1顺序任务卸载决策

1.In:G(V,E)

2.EntryTask←1

3.ExitTask←1

4.Tmin=T(1,1)

5.Forj←1 ton-1

//寻找入口任务EntryTask

6.Fork←jton-1

//寻找出口任务ExitTask

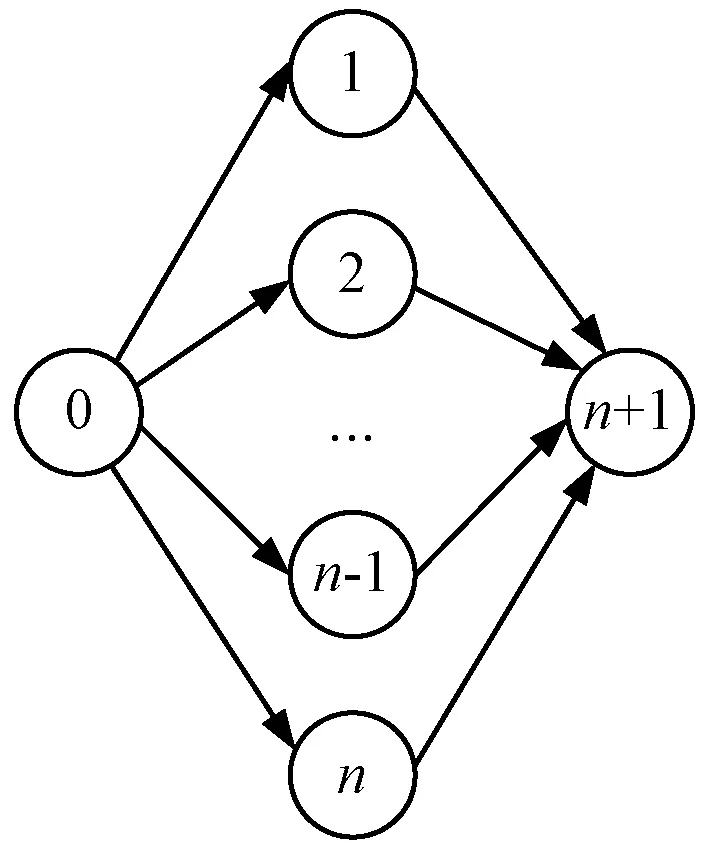
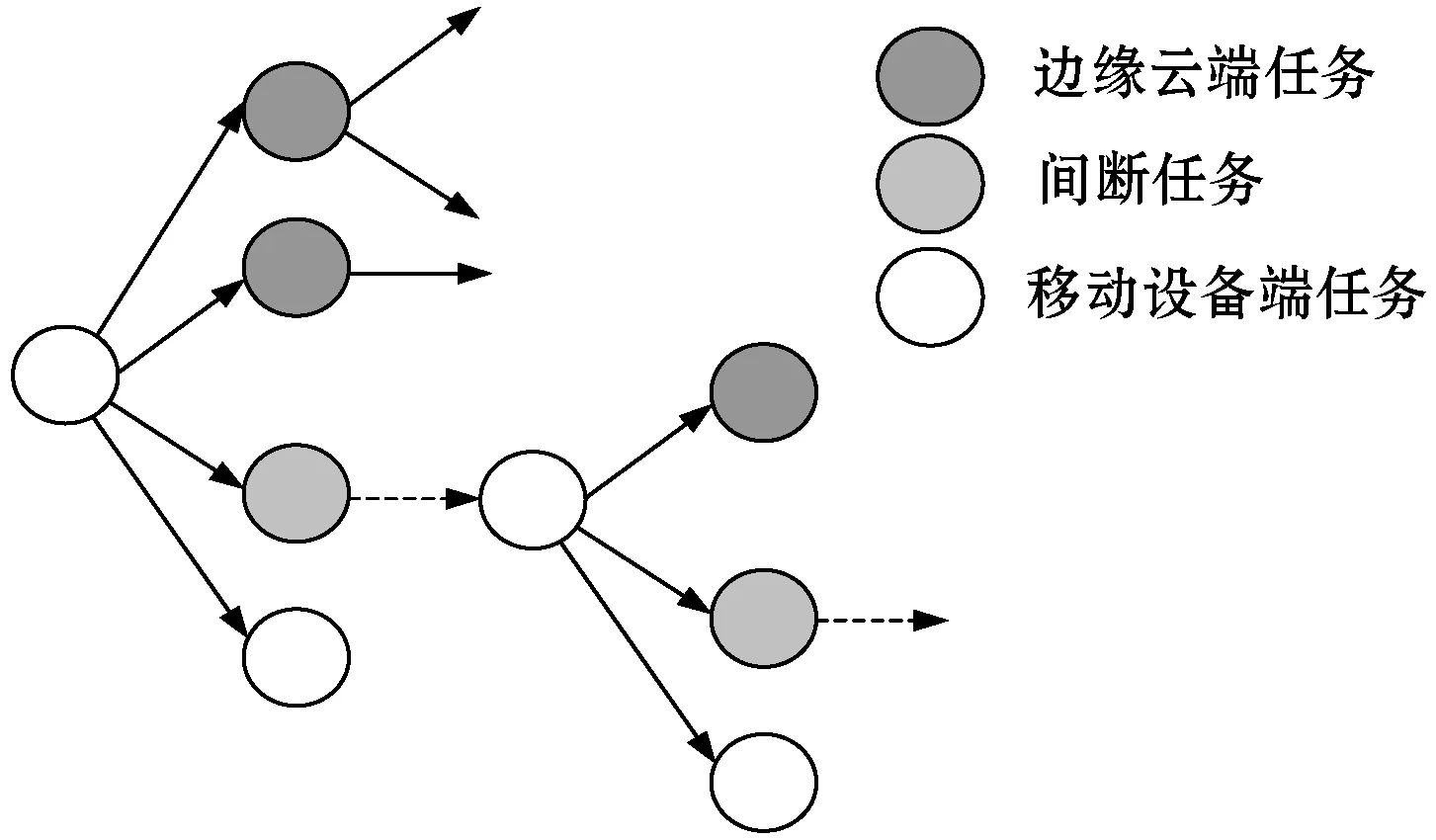
7.IfT(j,k)

8.EntryTask←j

9.ExitTask←k

10.Tmin=T(j,k)

11.End

12.Out:{Taski|j≤i≤k}

算法过程的详细说明:步骤1输入任务图结构,步骤2将任务1初始为入口任务,步骤3也将任务1初始为出口任务,步骤4入口至出口任务间的完成时间初始化为一个最小值,步骤5-步骤11遍历所有任务,在确定入口任务的情况下(步骤5),检测所有可能出口任务情形(步骤6),若得到的顺序任务群集的完成时间小于初始的最小值(步骤7),则在步骤8和步骤9分别更新入口任务和出口任务,并在步骤10更新完成时间最小值,最后在步骤12输出确定的入口任务与出口任务间的任务。入口任务至出口任务间的任务集群即为需要卸载至边缘云端执行的任务集合。

3.2 并发任务卸载

对于给定的任务图G(V,E),假设其开始于分叉(fork)任务0,终止于合并任务n。第一个分叉任务和最后一个合并任务通常在本地移动设备端执行,由于第一个任务(通常称为根任务)需要来自于本地设备的输入,而最后一个任务(通常称为终止任务)需要将生成数据传回本地移动设备。并发任务卸载的目标是通过最大化移动设备和边缘云端的并行度的方式最小化任务完成时间。以图2为例说明,在根任务0与终止任务n+1之间拥有n个并发任务,如果卸载过多任务至边缘云端,则移动设备必须等待边缘云端完成所有任务计算;如果卸载过少任务至边缘云端,则应用需要等待本地移动设备完成任务计算,这会延长总完成时间。任务卸载决策的最佳结果是:在边缘云端执行的任务与移动设备端执行的任务之间的终端任务等待时间应该尽可能减少。为了实现这一目标,计算任务卸载时,本地任务的完成时间需要尽可能接近于卸载任务的完成时间和数据传输时间之和。

图2 并发任务结构

对于一般并发任务结构图而言,决定哪些任务进行卸载是NP问题。研究表明,卸载任务通常是以集群形式进行,一旦一个任务被卸载,卸载其邻居任务时,通信代价可以有效降低,带来任务最终可以集群形式进行卸载(线性顺序任务结构中,连续任务也是集群形式)。然而,对于并发任务结构而言,寻找结构中的任务集群相对困难。本文的方法是:将并发任务图修剪为树结构,然后标识集群为子树,并寻找卸载子树。

1) 树的生成:算法通过剪枝每个任务输入链路将任务图转换为一棵树,直到每个任务仅有一个父任务为止。通过剪枝策略,可以降低卸载决策问题复杂度。然而,该过程需要均衡信息损失问题(任务依赖约束关系),这可能导致子最优的卸载决策。因此,算法仅剪枝数据负载最低的链路,以降低传输至子树以外的数据量。图3(a)所示为一个并发任务图,任务5和任务8是合并任务,其输入链路以网络传输时间标记。由于t3,5>t2,5、t5,8>t6,8>t7,8,对链路(2,5)、(6,8)和(7,8)进行剪枝后,得到的任务树如图3(b)所示。

(a) (b)图3 剪枝成树

2) 负载均衡的任务划分:令VC表示卸载至边缘云端的任务集合,VM表示本地移动设备端执行任务的集合,因此,VC+VM=V-{0,n},即从V中排除根任务0和终止任务n考虑任务卸载问题。由于卸载至边缘云端的任务为集群形式,则在树形拓扑中,若一个非叶子任务被卸载,则以该任务为根节点的子树中的所有任务均需要一起卸载。该卸载决策在分叉任务上作出,其子任务将作为入口任务的候选节点。令tree(i)表示以任务i为根节点的子树中的任务集合(包括i),定义Mi表示在移动设备端tree(i)中所有任务的执行时间:

(6)

Ci表示边缘云端tree(i)中所有任务的执行时间:

(7)

定义Ventry为卸载的入口任务集合,Ventry中每个任务为卸载子树的根节点。由于数据传输仅发生在树拓扑中的入口任务上,定义Tnet为边缘云端与移动设备端之间的数据传输总时间:

(8)

令TC表示边缘云端任务的执行时间:

(9)

由于子树任务卸载至边缘云端,假设相同子树中的任务在边缘云端顺序执行,且不在等待队列中重复输入,这表明仅需要计算入口任务到达时的排队时间。最后,定义TM表示移动设备端所有任务的完成时间:

(10)

为了最小化并发任务的完成时间,需要均衡边缘云端与本地移动设备的负载,使得移动设备端任务的完成应尽可能接近于边缘云端任务执行与数据传输时间之和。假设根任务在移动设备端执行,则任务卸载决策最优化问题可形式化为:

min|TM-TC-Tnet|

(11)

初始时,将VC设置为空集,这表明所有任务在本地移动设备。从根节点开始,如图4所示。根节点的子任务公式(6)定义的Mi的降序进行排列,i表示根的一个子任务。对子树中依次执行任务的卸载决策直到满足TM

图4 树的卸载

算法2并发任务卸载决策

1.In:G(V,E)

2.r=0(根任务卸载至边缘云)/r=1(根任务在移动设备)

3.Vnet=NULL

4.Ifr==1 thenVC=NULL

5.ElseVC=V-{0,n}

6.currentTask=root

7.while root has childen

8.i←0

9.while (2r-1)(TM-TC)>Tnet

10.Task child←currentTask.getChild[i]

11.Ifr==1 thenVC←VC+tree(child)

12.ElseVC←VC-tree(child);end

13.Ventry←Ventry+child

14.i=i+1

15.End

16.Ifr==1 thenVentry←Ventry+child

17.ElseVC←VC-tree(child);end

18.Ventry←Ventry-child

19.//rool back offload for break task

20.currentTask=child

21.end

22.out:VC

算法过程的详细说明:步骤1输入并发任务结构图,步骤2定义卸载决策因子,步骤3初始化一个任务集合,步骤4判定,若卸载决策因子为1,表明任务在本地设备执行,则卸载至边缘云端的任务集合为空,否则,剔除入口任务和终止任务,更新卸载任务集合,即步骤5。步骤6将根节点定义为当前任务,若该任务拥有子节点任务,则在步骤9-步骤15剪枝成树的形式更新入口任务,若为本地执行的任务,则直接将其子节点添加至入口任务集合以下,即步骤16,否则,删减以该节点为起始的子树,即步骤17。该过程需要在所有拥有子节点的任务节点上进行迭代,最后输出的集合即为整个任务图中需要卸载至边缘云端执行的任务集合。

3.3 通用任务卸载

本节描述如何合并算法1和算法2实现通用任务图的卸载决策。通用任务图由顺序的链式任务图和并发任务合并而成。为了实现通用任务图的卸载决策,将每个并发任务集合视为一个虚拟任务,使其得到一个线性拓扑图。如图5(a)的示例,每个并发任务子图表示为虚拟节点后,得到图5(b)。其中,图5(a)左侧任务结构图为Fork-join结构,图5(b)右侧任务结构图为并行结构。定义虚拟任务的计算权重为:

图5 通用任务结构

(12)

计算线性拓扑图的卸载决策后,某些虚拟节点将卸载至边缘云端,而一些虚拟节点又将在移动设备端执行。对于任意一种情形,利用算法2计算虚拟节点中并发任务的卸载决策,进而有效利用移动设备端和边缘云端的并行性。

当根任务和终止任务在本地移动设备执行时,利用式(11)实现负载均衡目标。对于并发任务子图的卸载决策而言,子图中的根节点和终止节点可能不在本地移动设备执行。引入变量r,r=0表示根节点在边缘云端执行,r=1表示根节点在本地移动设备端执行。将式(11)的任务卸载负载均衡目标修正为以下通用卸载负载均衡目标:

min|(2r-1)(TM-TC)-Tnet|

(13)

4 仿真实验

4.1 实验配置

以随机生成的任务结构图测试卸载决策算法性能,实验环境为MATLAB。任务结构图的生成重点考虑两个属性参数:(1) 任务规模,即有向图中任务的总数量;(2) 任务间的链接密度,以每个任务的平均出度数进行设置。任务出度表示在一个任务有向图中,从一个任务节点出发的有向边的条数。任务权重和连接权重通过均匀分布方式随机生成。设置本地移动设备的CPU的μm=1,表1给出了仿真实验中相关参数配置,其中,free代表参数为自由变量。四类参数配置中,取值为free时,其他三个参数则为固定值。为了对比算法性能,引入两种同类型的任务卸载决策算法,一种是文献[11]的ODE算法,一种是利用穷举算法OPTIMAL得到的理论最优解。由于在设定的任务规模下,可在有限时间内通过穷举法得到最优的任务卸载决策解,但任务规模增大时,穷举法的搜索时间复杂度将呈指数级增长,因此,引入该算法仅仅是用于衡量本文算法与理论最优解间的差距,并以此间接度量算法性能。

表1 参数配置

4.2 实验结果

图6表示任务图中任务数量对完成时间的影响。可以看到,本文算法得到的完成时间约为最优算法OPTIMAL结果的85%～90%,ODE算法的完成时间则与最优算法相距45%(20个任务)～75%(5个任务),任务规模较小时该算法表现较好,是由于较小规模任务量更加有可能以集群形式进行任务卸载。随着任务规模的增加,卸载任务更加分散,这会增加数据传输量,导致总体完成时间的递增。

图6 任务数量的影响

图7表示任务图中单个任务的平均出度对完成时间的影响,节点出度表示由任务节点出发的有向边的条数,通过任务图中总的有向边条数除以任务总数确定。可以看到,任务图中的链接密度对任务总的完成时间影响较小,说明该参数不会过度影响算法性能。ODE算法的性能从57%(平均出度为1)降低至46%(平均出度为8)。由于任务图中的链接密度的增加会导致任务卸载的数据传输代价的增加,因此,该算法较难作出最佳的任务卸载决策。

图7 任务平均出度的影响

图8表示网络通信带宽对于完成时间的影响。可以看到,随着网络带宽的增加,性能趋势呈凹状下降。本文算法在带宽为0.1时接近于最优算法的90%性能,至带宽为1.5时增加至95%。当带宽处于1.5至10区间时,算法性能出现轻微下降,原因在于算法可以以任务的序列形式将任务在本地移动设备上执行,这会导致更少的任务卸载至边缘云端。ODE算法在带宽为0.1时接近于最优算法的70%性能,至带宽为1时增加至50%。带宽从0.1变化至1时,ODE算法可以卸载更多任务进而降低完成时间,然后与本文算法相比,距离最优算法仍然较远,该算法对于任务卸载决策不是最优的,也没有考虑任务图的内在结构。随着带宽量的增加,ODE算法逐渐卸载其所有任务去边缘云端,导致其性能上升至70%。

图8 通信带宽的影响

图9表示边缘云端排队时间对于完成时间的影响。本文算法距离最优算法性能约为85%～90%,而ODE算法则是45%～55%。由于ODE算法没有考虑任务在边缘云端的排队时间,算法选择卸载的任务数量是平均相同的,与边缘云端排队时间无关,最终导致其完成时间是接近于线性的。

图9 边缘云端排队时间的影响

综合考虑以上结果可以看到,本文算法得到的完成时间总体接近于理论最优算法的85%,ODE则是接近于50%,其主要不足体现于两点:(1) 本文算法一次仅卸载单个任务,无法实现集群式的任务卸载决策,这样导致了过多频繁的任务卸载决策,尤其在网络带宽限制较多时,会出现较大的完成延时;(2) 本文算法没有考虑移动设备端与边缘云端的并行性。若给定带宽足够大,ODE算法会卸载所有任务至边缘云端,由于此时卸载任务的传输代价低于本地执行与云端执行时间之差。本文算法可以根据当前的负载状况对特定任务图结构作出最优卸载决策,可以得到与理论最优解更接近的解。

5 结 语

为了实现移动边缘云环境中移动设备任务执行时间的优化,提出一种任务卸载决策算法。算法考虑了更为普遍的混合任务结构类型。对于顺序任务构成的线性拓扑任务图,算法可以找到最优的卸载任务;而对于并发任务的通用拓扑任务图,算法可以实现任务卸载的更好负载均衡。仿真实验结果证明,与基准算法相比,本文算法得到的任务完成时间与理论最优解更为接近,任务完成效率更高。