基于局部编码和多头注意力模型的电力系统暂态稳定性评估

谷广超 轩克辉

(河南工业大学漯河工学院 漯河 河南462000)

0 引 言

电力系统暂态稳定是指电力系统在遭受大干扰时发电机组保持同步运行并过渡到新的安全状态或恢复到原来稳定运行状态的能力[1]。随着经济社会的用电需求不断增加,电力系统的传输趋近于容量极限,任何突发事件都有可能会引起电力系统严重瘫痪或大规模断电。

实时暂态稳定性评估(Transient Stability Assessment,TSA)是预防电力系统级联故障,避免电力系统不稳定和大规模停电的重要手段,同时也是保障电力系统安全和稳定分析的必要方法,引起了工业界和学术界的广泛关注。

目前,暂态稳定性评估的主要研究方法可以分为时域仿真法[2-3]、直接法[4-5]和机器学习法[6]。时域仿真法采用逐步数值积分的策略,通过求解电机动态变化的微分方程组,获取电机转子角随时间的变化。但是该方法一方面高度依赖电网元件参数,另一方面由于电力系统大体量的非线性系统,方程求解过程十分复杂,容易出现“维数灾难”,计算速度缓慢且无法得到稳定裕度。

直接法从能量角度入手,构造李雅普诺夫函数,通过故障清除点和临界稳点对应的李雅普诺夫函数值差的正负来判别系统的稳定性,避免了求解微分方程的复杂过程。但是直接法大多以双机失稳模式为前提,可扩展性有限,结果可靠性不强。

基于机器学习的TSA方法分为两步,首先是离线训练,在离线状态下学习输入(电力系统的特征)和输出(稳定性状态)之间的映射模型,达到很好的模型拟合程度和泛化预测性能。然后是在线预测,利用该预测模型进行在线暂态稳定性评估。该方法可以在线快速、准确地确定电力系统的稳定性,是一种最具应用前景的方法。

该方法的研究主要集中于不同机器学习算法的应用,包括传统的机器学习算法和深度学习算法。传统机器学习算法包括多层感知机(Multi-Layer Perceptron,MLP)[7]、支持向量机(Support Vector Machine,SVM)[8]、决策树(Decision Tree,DT)[9]和极限学习机(Extreme Learning Machine,ELM)[10]。基于传统机器学习算法的TSA方法可以避免对电力系统复杂的物理机制进行建模的过程,与上述两类方法相比,具有数据需求少、决策速度快和泛化能力强的优点。然而传统机器学习算法的网络结构简单,层数较少,特征提取能力有限。另外,都需要人工参与提取输入数据的特征,增加了人为主观性,推广性不强。

深度学习算法的模型结构更加复杂,层数较深,面对复杂、高维的非线性电力系统数据具有更强的特征提取能力,并且在整个特征提取过程中无须人工参与。目前,深度学习模型在TSA中的应用尚处于起步阶段,不同的模型结构在不同数据结构上的特征提取能力具有较大差异。考虑到电力系统暂态过程是从一个稳态过渡到另一个稳态或者失稳态的过程,系统的物理量测值(如电压、电流、功率和发动机相角)具有明显的时变特性,是标准的时间序列数据,而一维卷积神经网络和循环神经网络擅长处理此类数据,因此研究主要集中于基于卷积神经网络(Convolutional Neural Networks,CNN)[11-14]和循环神经网络(Recurrent Neural Network,RNN)[15-18]。然而卷积神经网络只能利用多个一维卷积核提取局部特征,循环神经网络难以处理长距离依赖关系,二者对电力系统数据建模时都缺乏对全局信息的考虑;另外电力系统量测数据中存在多组重点关联关系,例如电压、电流和功率,电压和相角,有用功、无用功和总功等,二者在训练时无法重点突出这些关系。

Transformer[19]是当前自然语言处理领域的主流模型,在机器翻译、文本分类、图像生成和语音识别等任务中均获取了最优结果。其成功的关键在于大量采用多头注意力模型对数据进行全局建模,从整个样本序列中挖掘与当前预测元素关系最紧密的上下文元素,具有关注重点关系特征的能力。然而,Transformer无循环结构,需要对序列元素的位置信息进行编码,尽管引入三角函数对位置进行编码,但是效果有限,导致多头注意力机制忽略了很多局部的特征,因此位置编码应该针对具体任务具体设计[20-21]。

综上所述,本文结合局部RNN可以提取包含位置信息的局部特征和多头注意力模型可以全局建模关注全局显著特征的特点,提出一种基于局部编码和多头注意力模型的暂态稳定性评估框架。该框架由R-Attention层、全连接层和softmax层串联而成。R-Attention层以局部RNN结构和多头注意力模型为主,首先,利用局部RNN结构提取电力系统量测值的局部特征;然后,利用多头注意力模型对所有局部特征进行建模,通过多头注意力机制计算各局部特征的长距离依赖关系,挖掘之间显著的关联特征表示。最后,将该特征表示输入到全连接神经网络层和softmax层,输出识别概率。

1 模型构建

本文根据RNN和多头注意力模型的工作特点, 构建了基于局部编码和多头注意力模型的暂态稳定性评估框架模型,其结构如图1所示。

该框架主要由R-Attention层、全连接层和softmax层串行而成,[CLS]是暂态状态数据的标签符,表示电力系统现在是稳态还是欠稳态,下面进行具体介绍。

1.1 R-Attention编码层

R-Attention层由6层R-Attention模块堆叠而成,每个R-Attention模块由PartialRNN层、多头注意力层和位置全连接前馈网络层组成,如图2所示。

图2 R-Attention编码层

电力系统暂态状态数据具有很强的局部特征,PartialRNN层用于获取具有该序列数据局部信息和位置信息的向量表示;多头注意力层用于挖掘所有局部信息之间的长期依赖,即提取序列全局特征;位置全连接前馈网络层用于对全局特征进行非线性变换。这三层网络的输入与输出之间分别添加一个残差连接,进行加和并归一化操作,优化网络训练深度。

(1) PartialRNN层。与之前大多数工作将RNN应用于整个输入序列不同,本文在输入序列的每个目标位置构造一个包括M个连续位置并在目标位置结束的窗口,将原始的长序列利用窗口重组为多个短序列,这些短序列仅包含局部信息,由一个参数共享的RNN分别处理,记为PartialRNN,如图3所示。

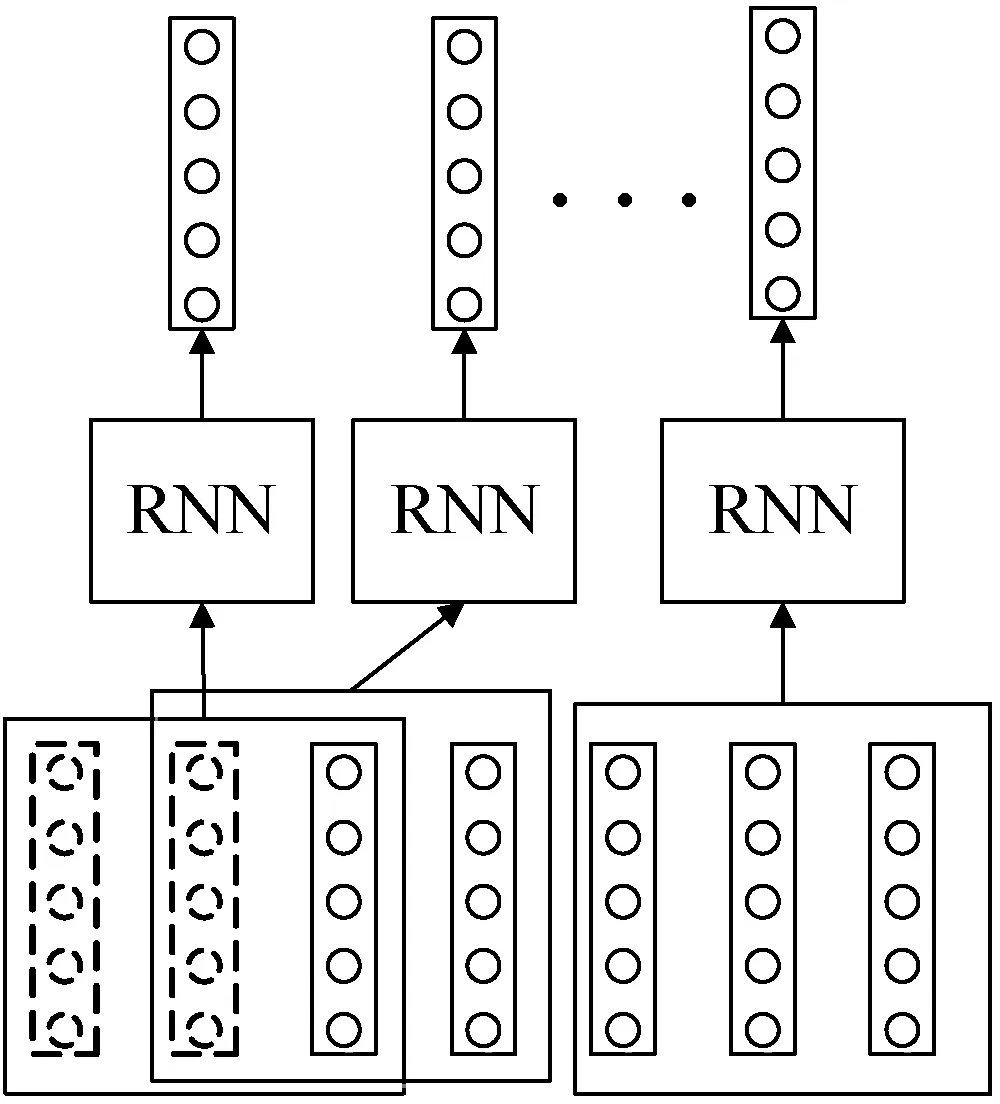
图3 PartialRNN工作示意图

图3中以窗口大小M等于3为例,虚线位置是填补位。设定窗口M内包括的位置为xt-M-1,xt-M-2,…,xt,经过RNN顺序处理后,每个位置都会产生一个隐向量输出,以最后一个位置的隐向量输出作为短序列的向量表示,如式(1)所示。

ht=PartialRNN(xt-M-1,xt-M,2,…,xt)

(1)

RNN代表任何循环神经网络单元,例如Vanilla RNN、LSTM和GRU等。一个长序列经过PartialRNN处理后可得到多个具有局部信息和位置信息的隐向量表示,如式(2)所示。

h1,h2,…,hn=PartialRNN(x1,x2,…,xN)

(2)

(2) 多头注意力层。注意力机制的本质是将一个查询向量和一组键值向量对映射到输出,查询向量与键向量用于计算每个值向量对应的权重,值向量的加权和为注意力输出。多头注意力层由多个点积注意力[22]操作组成,如图4所示。

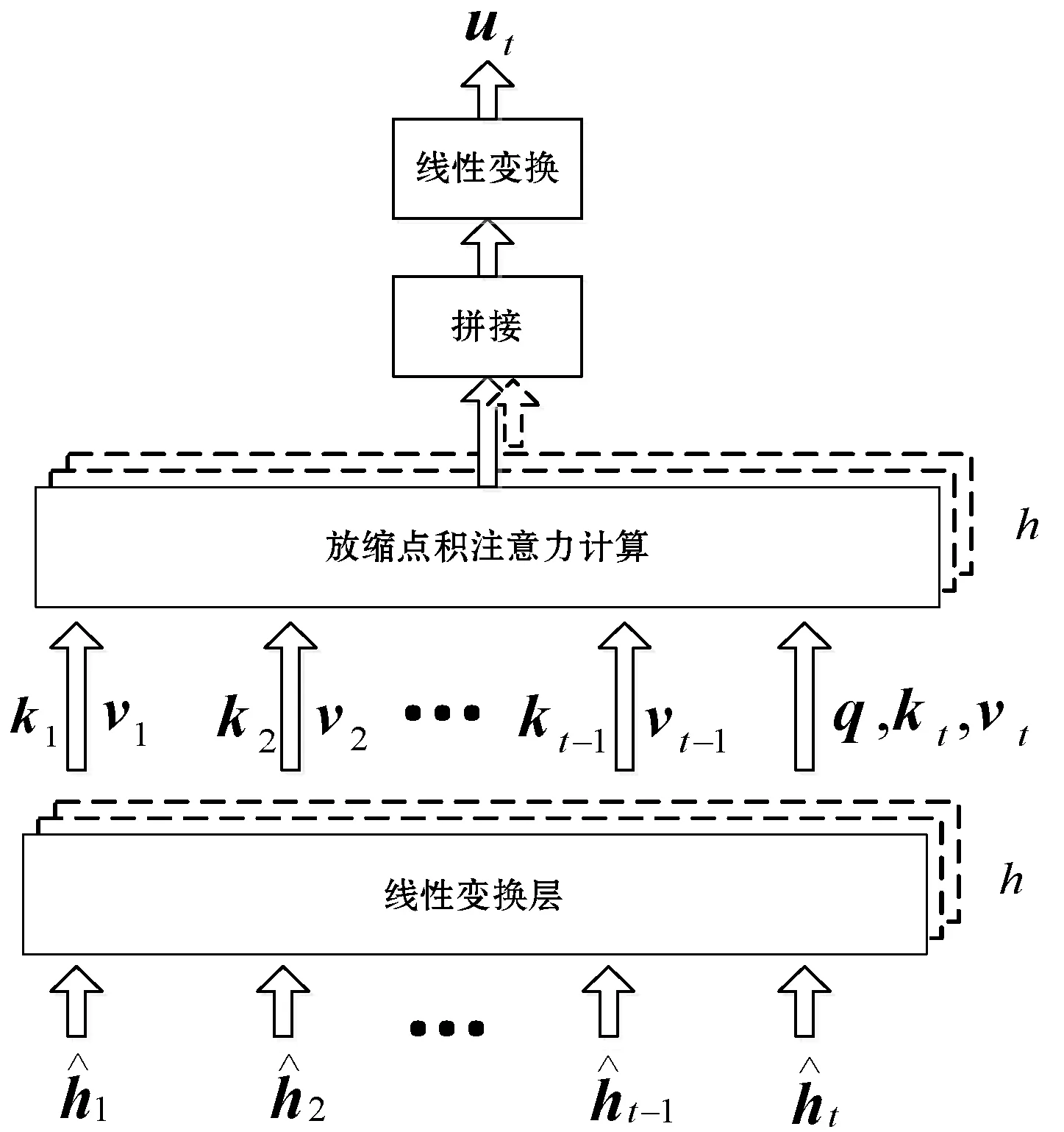
图4 多头注意力层计算流程

图4中,多头注意力层进行h次点积注意力操作,头数为h,维数记为dmodel。其输入为PartialRNN层输入与输出加和并归一化的结果,经过线性变换得到位置t的查询向量和所有位置的键值向量,如式(3)和式(4)所示。

(3)

(4)

式中:Wq∈Rdmodel×dk,Wk∈Rdmodel×dk,Wv∈Rdmodel×dv均为线性变换层的映射矩阵,每次点积注意力的映射矩阵均不同。q和ki中每个向量的维度为dk,vi中每个向量维度为dv,将h次的注意力计算结果通过拼接和线性变换得到多头注意力的结果,如式(5)所示。

(5)

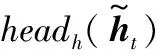
(6)

{a1,a2,…,an}=

(7)

(3) 位置全连接前馈网络层。位置全连接前馈网络层(FFN)分两层,用于处理每个位置的多头注意力计算结果,其输入和输出的维度相同。第一层的激活函数是ReLU,第二层是线性激活函数,多头注意力层输出为ut,则FFN可表示为:

FFN(x)=max(0,utW1+b1)W2+b2

(8)

式中:W1、b1和W2、b2分别是两个激活函数的参数。R-Attention编码层利用PartialRNN层、多头注意力层和位置全连接层不断交叠得到最终的输入序列表示。

1.2 全连接层和softmax层

对于一个样本容量为N的训练集Q,给定一个电力系统量测序列x1,x2,…,xN和对应标签y,[CLS]在R-Attention编码层最后一个隐藏层输出记为TC∈Rdmodel,经过全连接层和softmax层后对y进行预测,如式(9)所示。

P(y|x1,x2,…,xN)=softmax(TCWf+b)

(9)

式中:Wf是全连接层的权重矩阵,b为偏置,P(y|x1,x2,…,xN)是softmax层计算的概率结果,记为y′。则模型训练的目标为最小化交叉熵损耗函数L(Q),如式(10)所示。

(10)

2 实验与结果分析

2.1 实验数据

2.1.1初始特征构建

初始特征作为整个模型的输入,对模型的性能具有重要影响。目前没有统一的初始特征构造方法,一般常用“三段式”特征[23]和受扰后轨迹特征[24]。参考文献[15]和文献[16]特征构建的经验,同时考虑数据获取的实时性和模型框架的特点,本文以母线电压幅值和相角、支路有功功率和无功功率构建“三段式”特征。“三段式”特征包括故障发生前的静态特征,故障发生时和故障切除后动态特征,初始特征采样时间如图5所示。

图5 初始特征采样时间

图5中特征点采样区间为[tf-2,tc+k],其中tf为故障发生时刻,tf-2为故障发生前2个周期的稳态时刻,tc为故障切除时刻,tc+k为故障切除后k个周期的时刻。对于容量为N的样本集,单个样本表示为X(i)=[x1,x2,…,xt,…,xs]T,t时刻特征向量表示为xt=[V1,t,…,Vu,t,…,θ1,t,…,θu,t,P1,t,…,Pr,t,Q1,t,…,Qr,t]T,式中:u代表母线编号;r代表支路编号;Vu,t和θu,t分别代表第u条母线t时刻的电压幅值、相角;Pr,t和Qr,t分别代表第r条支路t时刻的有功功率、无功功率。

2.1.2样本生成

大多研究[14-16]均以新英格兰10机39节点系统为测试电网,本文为方便实验对比也采用该系统进行验证。该测试系统由39 条母线、10 台发电机、19 个负荷和34条传输线组成,基准频率为60 Hz。利用PSS/E软件进行时域仿真,仿真设置参考文献[14],发电机采用GENROU模式,负荷为恒阻抗模型,步长为0.008 3 s。负荷水平从80%起以10%为阶梯增长至120%,共5种负荷水平,同时调整发电机出力使潮流收敛。在每种运行方式下对各支路施加三相短路故障,故障设置在10%、25 %、55%、75 %和90%五个不同的位置。故障施加时刻为1 s末,解除时间为1.4到1.8 s之间,随机设置12个不同的故障解除时刻。固定初始特征的响应时间为3个周期,由于故障解除时间不同,采样的点数不同,最长的采样序列有88个点,每个点的特征维度为170。为了使模型快速正常训练,对初始特征归一化后,以最长序列为准,对不足88个点的序列补零,统一样本尺寸。仿真时长为4 s,如果系统中任意两个发电机转子角度之差在仿真结束时小于360°,则判定为暂态稳定,否则为暂态失稳。共生成12 366个样本,其中稳定样本8 941个,失稳样本3 425个。随机抽取10 000个样本作为训练样本,其余2 366个样本作为测试样本。

2.2 评测标准

本文以准确率(Accuracy,Acc)、F1值和误报率(False Positive Rate,FPR)为评测指标,综合评估暂态稳定评估系统的性能。准确率和F1值越高,说明模型性能越强。由于电网对失稳状态准确判定的要求高于对稳定状态的准确判定,因此采用FPR指标,FPR值越小,模型对失稳状态的判定越准确。首先定义混淆矩阵,如表1所示。

表1 混淆矩阵

TP和TN分别为稳定样本和失稳样本被正确分类的数量,FP为失稳样本被判为稳定样本的数量,FN为稳定样本被判为失稳样本的数量。根据混淆矩阵计算准确率、F1值和误报率。

(1) 准确率(Acc)计算表达式为:

(11)

(2) F1值计算表达式为:

(12)

(3) 误报率(FPR)计算表达式为:

(13)

2.3 实验设置与结果分析

本文选取文献[14]和文献[15]的方法作为对比方法,分别利用一维卷积神经网络和双向长短期记忆网络构造评估模型,参照文献中最优的模型参数对本文构造的数据集进行评估,测试结果分别记为1D-CNN和Bi-LSTM。

按照2.1.1节中样本获取的方法得到每个样本的维数为88×170,使用TensorFlow深度学习框架构造模型结构。根据模型训练经验,选取LSTM模型作为PartialRNN的基本单元,LSTM层数为2,其隐藏层节点数为600。全连接层的隐藏节点数量为768,优化算法选取Adam[24],令β1=0.9,β2=0.98,ε=10-9。迭代次数为1 000,epochs设置为88,每批数据batch_size大小为256,学习速率为2e-5,本文方法测试结果记为RNN-TRAM。

实验软硬件配置如下:操作系统Centos7.5 64位操作系统,CPU为16核Intel Xeon E5-2680 2.7 GHz,内存为128 GB,配备2块显存为32 GB的GTX Tesla V100独立显卡。

2.3.1PartialRNN窗口大小M的分析

PartialRNN是本文提取电力系统量测数据局部特征的关键结构,窗口大小的选取对模型性能具有重要影响。令窗口大小M在[0,10]内取值,以1为步长训练模型进行暂态稳定性评估,多头注意力模型头数随机设定为5,以Acc、FPR和F1值为评测标准,结果如图6所示。

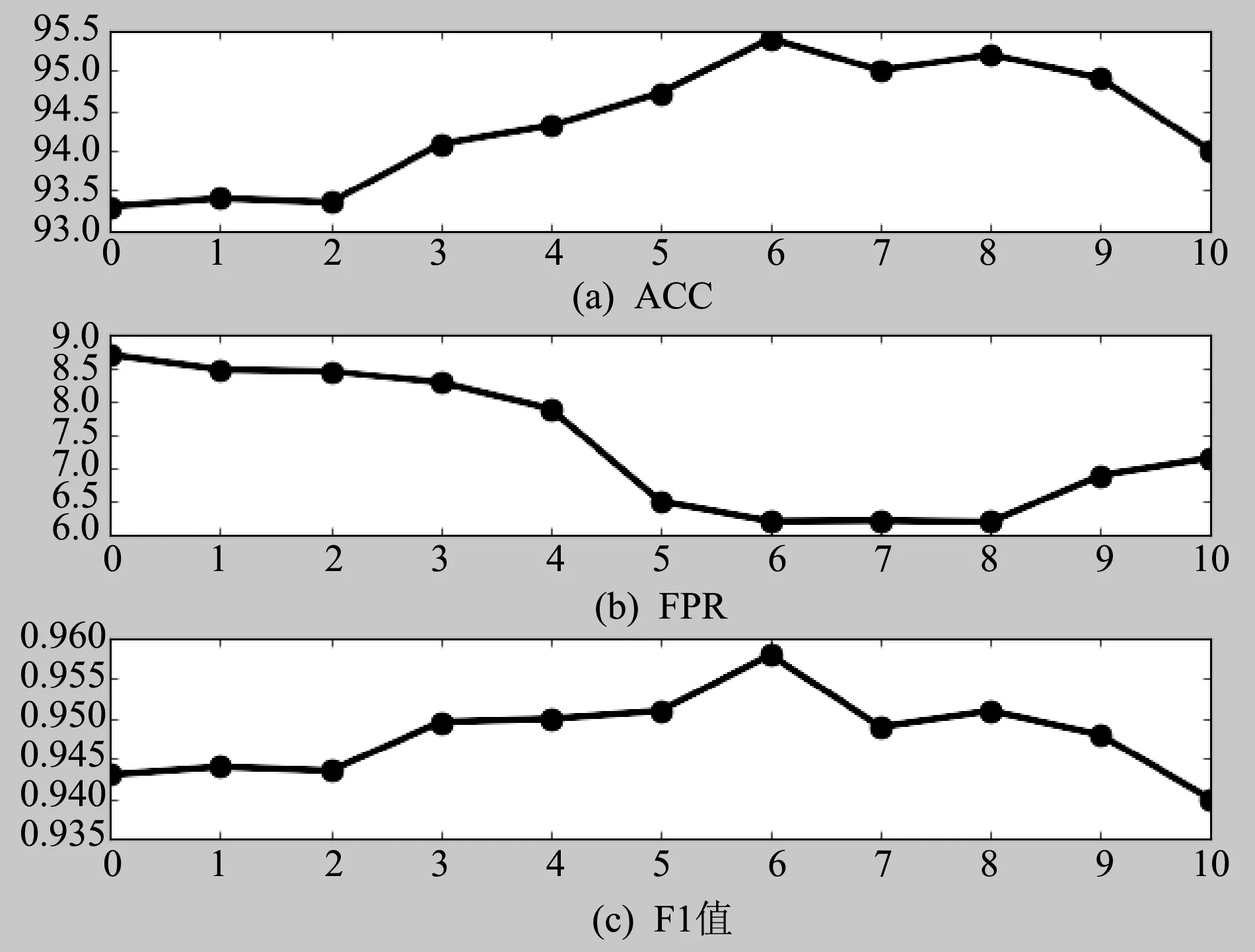
图6 PartialRNN窗口大小对暂态稳定评估的影响评测

由图6可知,窗口在[0,2]区间时,PartialRNN提取的局部信息有限,Acc变化不明显。窗口在[3,6]的区间时,窗口内元素不断增多,PartialRNN开始有效地提取局部特征信息,Acc显著提高;当窗口继续增大时,Acc变化不明显,且有降低的趋势。FPR在窗口区间[0,4]时无明显降低,在窗口为[5,8]时显著降低,取得较好结果;F1值在窗口为6时取得峰值。综上,窗口大小以6作为最佳参数。

2.3.2多头注意力模型中头数h的分析

单头注意力计算关注到的序列关系有限,而量测数据中的功率、电压、幅角、有用功率、无用功率、总功率和分支功率等数据之间关系多样,需要进行多次自注意力计算。因此,本节分析多头注意力计算中头数h对暂态稳定评估的影响。令PartialRNN窗口大小为6,h在[2,14]内取值,以2为步长训练暂态稳定性评估模型,在测试集进行暂态稳定性评估,以评测指标准确率分析,结果如图7所示。

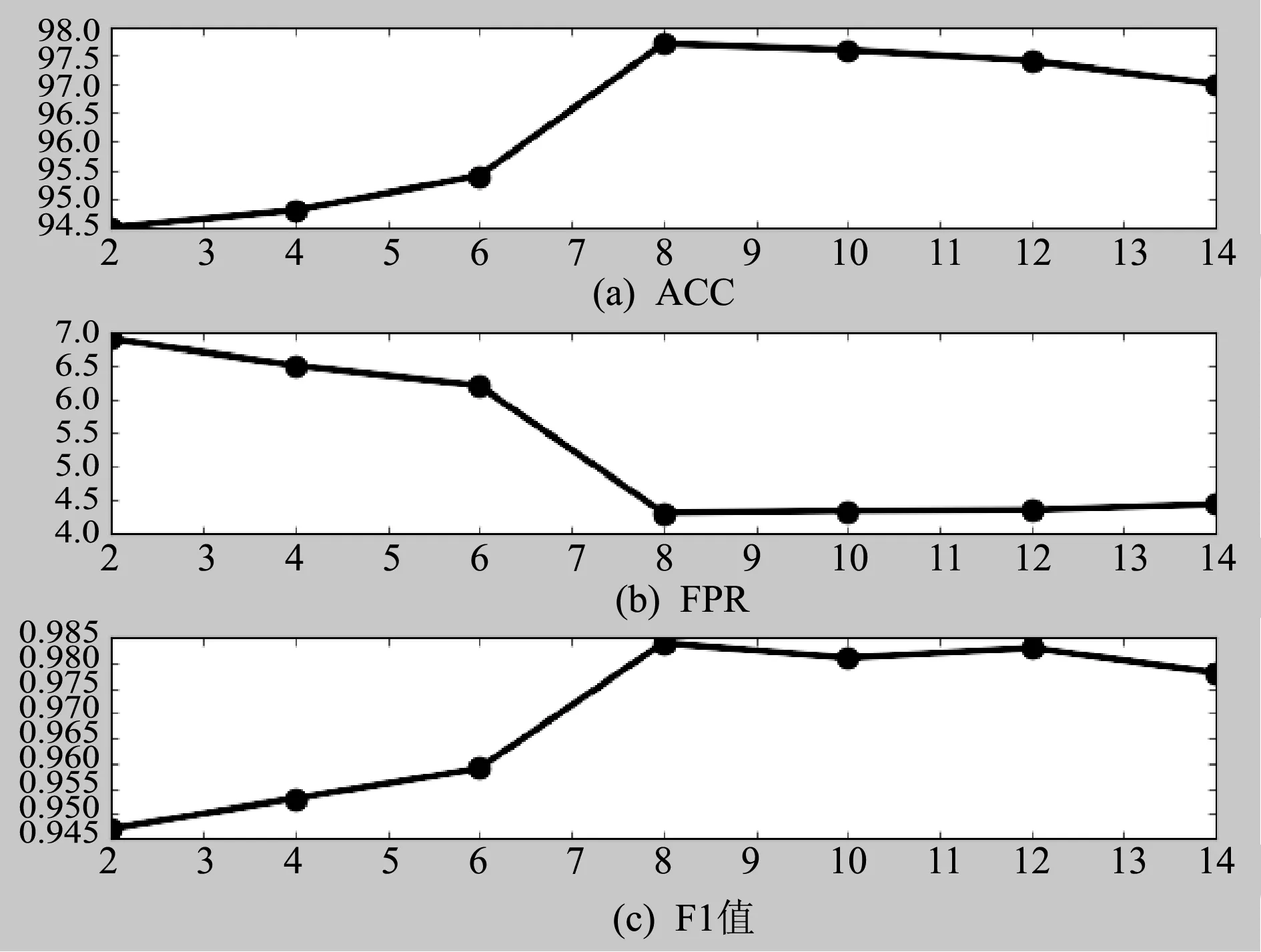
图7 多头注意力模型头数对暂态稳定评估的影响评测

由图7看出,在[2,8]的区间内,Acc和F1值的总体趋势是随着h的增加而增大,FPR随着h的增加而减小,从局部特征中提取的关联关系越来越多样,说明多头注意力机制对提升检测性能有重要作用。当h为8时达到峰值,随后三者均趋于平稳,可以推测量测样本数据中的母线电压、相位角、各支路有功功率和无功功率等有8种左右的内在关系,符合数据的真实特征。

2.3.3综合实验分析

结合前两节的实验结果,令PartialRNN窗口大小为6,多头注意力的头数为8,本文方法和两种对比方法进行综合对比实验,测试结果如表2所示。

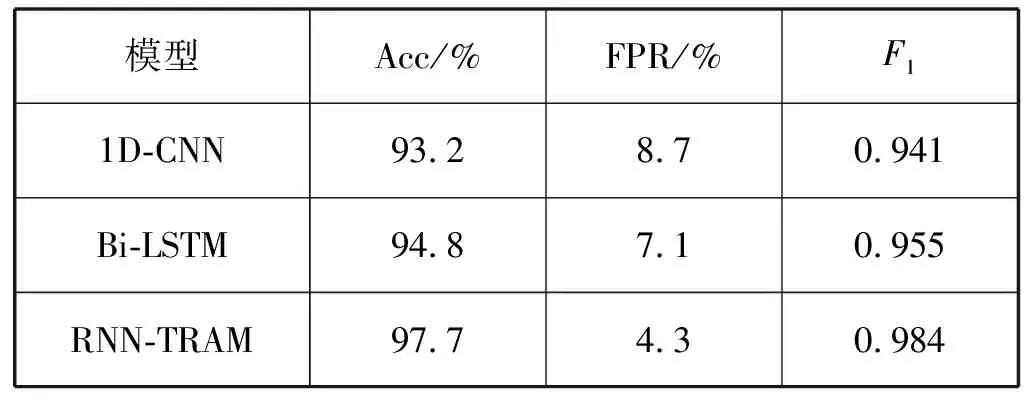
表2 综合实验结果

在表2评测结果中本文方法取得了最优结果,说明了本文方法的合理性和有效性。实验中,RNN-TRAM较次优结果Bi-LSTM的Acc提高3.05%,F1提高3.04%,FPR降低39.44%。这是由于本文框架先对“三段式”暂态状态量测值进行了局部特征抽取,该局部特征包含稳态到失稳、失稳到失稳和失稳到稳态三个阶段过渡的特征,然后利用多头注意力模型可以对输入的多个局部特征在不考虑距离的前提下进行全局建模。而Bi-LSTM 和1D-CNN框架只能局部特征的一种进行提取作为表征,无法恰当融合三阶段特征,因此本文框架对多个局部特征进行全局建模抽取的综合特征更能代表“三段式”量测序列的暂态状态特征。另外,从三种方法样本检测结果中分析,Bi-LSTM和1D-CNN方法检测出的样本仅体现出了有功功率和电压相角(功角)强耦合,无功功率和电压幅值强耦合的这类局部特点。RNN-TRAM检测出的样本不仅体现以上局部特征,还体现了各支路有功功率总和和无功功率总和在一定范围内波动的全局特征。

2.3.4特征可视化分析

为了更加直观地体现三种方法的特征提取能力,本节将2 366个测试样本输入到完成训练的1D-CNN、Bi-LSTM和RNN-TRAM三种模型中,采用t-SNE算法[25]将三种模型输出的高维特征降维至二维平面,利用可视化工具包matplotlib进行展示,如图8-图10所示。

图8 1D-CNN特征提取可视化结果

以上三幅图中,蓝色点代表暂态稳定样本,红色点代表暂态失稳样本。由图8和图9可以看出,1D-CNN和Bi-LSTM对稳态样本和失稳样本的区分存在偏差,存在较多失稳状态被判定为稳态的情况,即FP值较大;由图10可以看出,RNN-TRAM对样本几乎呈现出线性分割的状态,对失稳状态样本的误判仅存在于类别边界部分,具有强于1D-CNN和Bi-LSTM的暂态稳定评估能力。

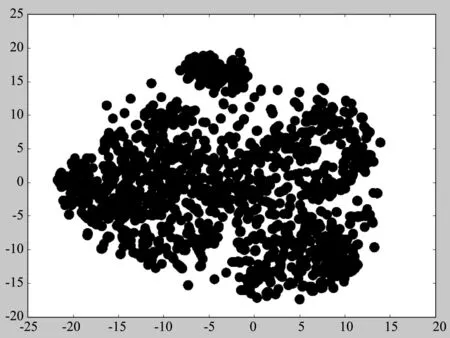
图9 Bi-LSTM特征提取可视化结果

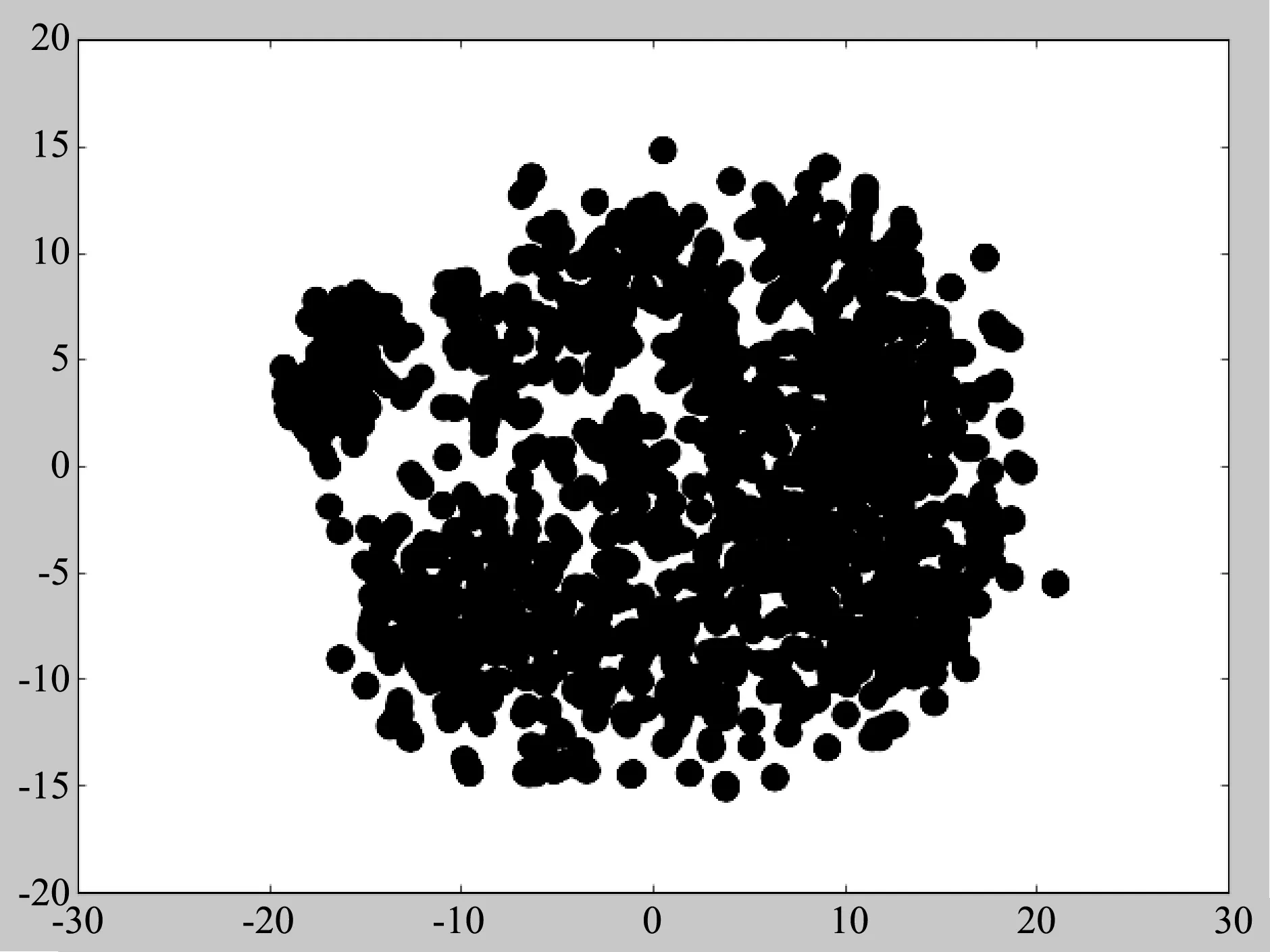
图10 RNN-TRAM特征提取可视化结果

3 结 语

本文提出一种基于局部编码和多头注意力模型的暂态稳定性评估框架,通过引入多头注意力模型解决了循环神经网络和卷积神经网络无法对暂态状态量测数据进行有效的全局建模问题,同时结合局部RNN结构,解决了多头注意力模型在建模时对局部特征关注缺失和缺少位置编码的问题,有效地提高了暂态稳定性评估性能。下一步准备在电网节点规模更大的模拟环境中测试本文方法的有效性。