基于机器学习偏差校正的GARCH波动率模型预测

许 敏 盛静文 袁 欣

(上海工程技术大学数理与统计学院 上海 201620)

0 引 言

科创板于2019年6月13日正式开板,其市场定位是实现资本市场对科技创新的融合,不仅能提升服务科技创新企业能力、增强市场包容性、强化市场功能,而且与目前的主板、创业板、中小板和新三板等交易市场一起,形成更丰富、多层次的融资体系,更好地发挥资本市场对实体经济尤其是创新型经济的支持力度。因而,科创板势必将对我国A股市场的波动性产生影响。为此,本文旨在研究科创板的设立对我国股票市场波动性的影响,并基于机器学习对GARCH波动率模型的预测偏差进行校正,以期提高波动率模型的预测精度从而对股票市场的风险更好地进行管理和控制。

波动率是度量标的资产投资收益不确定性的重要指标,由于真实的波动率无法直接观测,因此构建合理的波动率模型来估计真实波动率显得尤为重要。GARCH族模型是目前金融风险管理等领域最广泛使用的模型,其具有良好的统计特性,阐明了金融资产收益率序列波动的重要特征。但是它损失了大量的市场高频交易信息,对波动率的估计存在偏差。近年来,随着信息技术的快速发展,机器学习方法已被应用于波动率的预测中。Santamaría等[1]将混合遗传算法和支持向量机回归相结合(SVRGBC)对波动率进行预测,研究发现SVRGBC模型的预测能力优于GARCH模型。Gavrishchaka等[2]基于S&P500指数,运用SVM对股市波动率进行预测,发现其效果优于主流的波动率模型。Liu[3]利用LSTM模型对S&P500和AAPL指数的波动率进行建模,研究发现对于较长区间的波动率预测,其预测效果优于GARCH模型。Hamid等[4]用ANN模型预测标普500指数期货期权的波动率,结果发现神经网络对波动率的预测效果优于隐含波动率预测。Fu等[5]运用改进的支持向量机来预测人民币汇率波动,发现其预测准确性和统计准确性方面优于所有其他基准模型。但是将机器学习算法和波动率模型相结合的研究还远远不足,尤其是在股票市场的波动率预测方面还比较少[6-7]。

GARCH模型对前期波动率记忆过强,不能对新的波动变化迅速做出反应,而机器学习模型对数据的要求和假设条件较少,能够处理多样化和复杂结构的数据。为了将GARCH模型和机器学习算法各自的优势相结合,进一步研究科创板的设立对我国股市波动的影响,本文利用机器学习算法对GARCH模型捕获的波动率偏差进行修正,提出一种基于机器学习偏差校正的混合模型来预测股票市场的波动率,以期提高股票市场收益率波动性的准确性,为预测金融市场波动率提供一种新思路,进而为股市的风险预测、股票投资者和决策者提供参考。

1 理论基础

1.1 GARCH模型

传统时间序列模型假设金融资产的方差为常数,这一假设违背了金融市场价格波动的实际特征。为此Engle(1982)[8]利用添加的残差滞后项的平方及其权重来描述主体波动的方差性,继而构建了经典的自回归条件异方差(ARCH)模型:

(1)

为了克服实际应用中的高阶ARCH模型参数估计过多而引起的较大误差的不足,Bollerslev(1986)[9]基于滞后p期的条件方差提出了GARCH(p,q)模型:

(2)

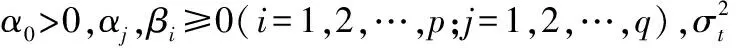
1.2 BP神经网络模型

BP神经网络模型[10]是一种误差反向传播的多层前馈神经网络,是目前神经网络模型中最具代表性且应用最普遍的模型,主要包括输入层、隐藏层和输出层,每一层都有若干个神经元。本文所使用的神经网络架构为5-7-4-1,即有5个输入神经元,7个隐藏神经元的第一层隐藏层,4个隐藏神经元的第二个隐藏层,一个输出层,其结构如图1所示。

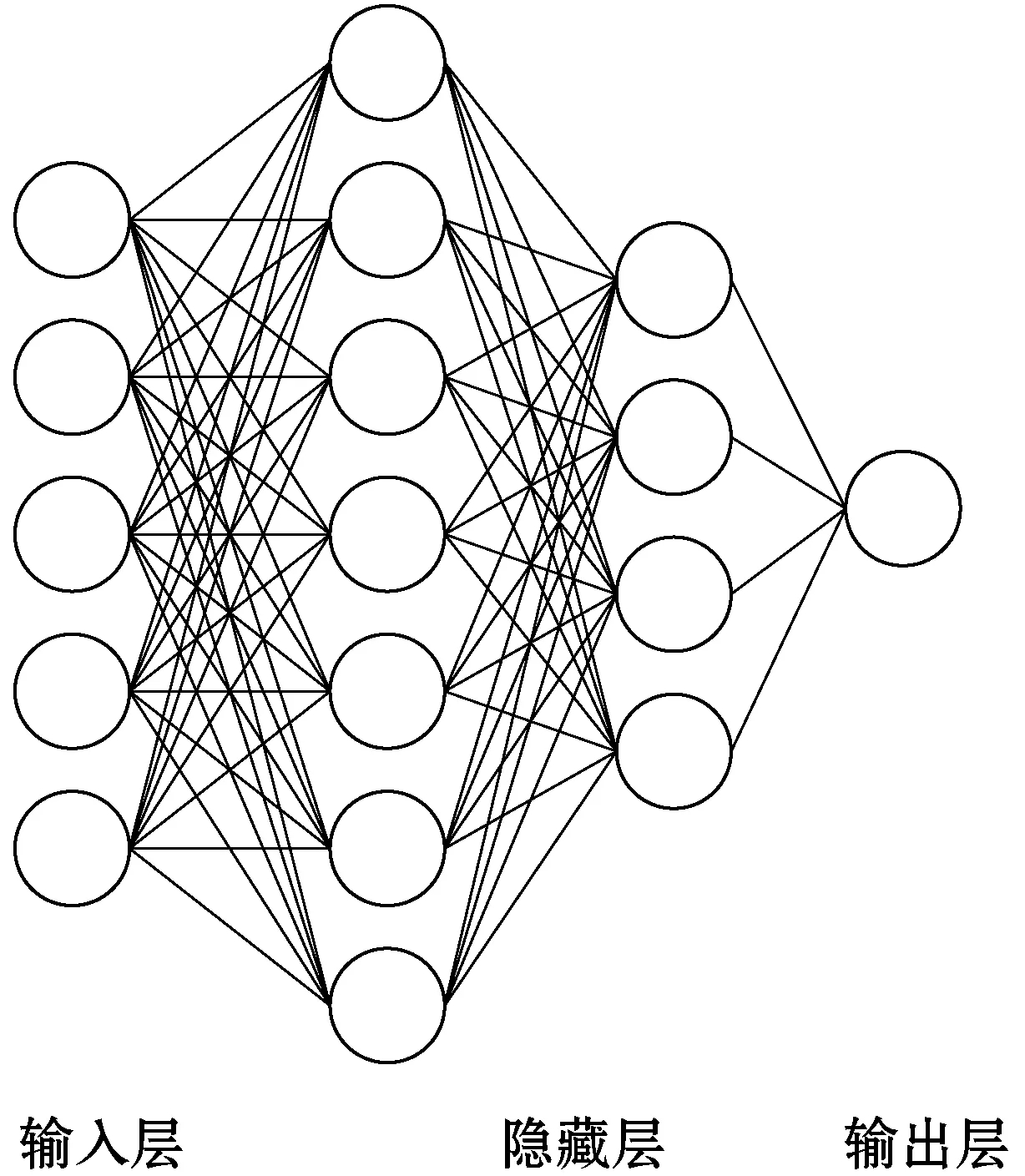
图1 BP神经网络模型结构

1.3 随机森林回归

随机森林回归(RF)[11]是一种以决策树为基函数的集成学习。通过自主采样法构建不同的训练数据集以及不同的特征空间来产生一系列有差异的决策树模型,最终结果通常取平均值。具体的算法流程如图2所示。

图2 随机森林回归原理

1.4 支持向量机回归

支持向量机回归(SVR)[12]是高效的监督学习方法。与其他回归模型不同的是,SVR模型先构建一个误差范围,那么落在误差范围内的预测值均被视为预测正确,最后根据误差间隔的大小确定回归模型。假设训练数据为{(xi,yi),i=1,2,…,n},SVR模型可通过映射函数φ(·)将数据从低维空间映射到高维空间,即:

w·φ(x)+b

(3)

式中:w为权重向量;b为常数;k(xi,x)为核函数;f(x)为预测值,与实际值yi之间存在一定的误差,所以SVR模型的标准形式为:

(4)

(5)

式中:Lε是不敏感损失函数;ε是不敏感损失;C是惩罚项。通常情况下,惩罚项越大,模型训练的精度就越高。SVR中常用的核函数包括:径向基函数和多项式函数等。

1.5 XGBoost回归

XGBoost回归[13]是以回归树(CART)作为基学习器的梯度提升算法。相对于其他提升算法,XGBoost控制了模型复杂度,提高了收敛速度和收敛精度并且防止过拟合。其主要流程如图3所示。

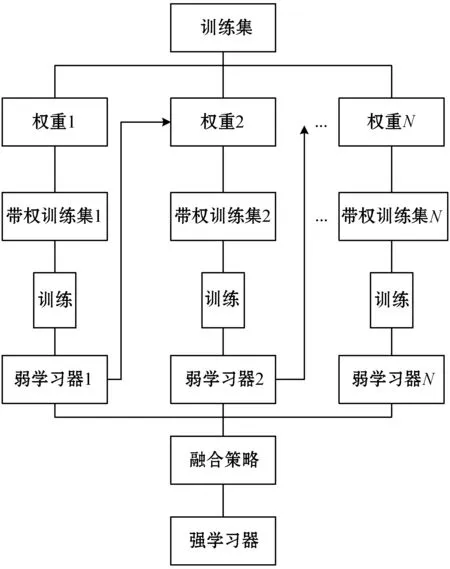
图3 XGBoost回归原理

1.6 基于机器学习偏差修正的波动率预测模型

本文将滞后一期的真实波动率、沪深300指数的收盘价价格极差、收盘价、成交量及滞后两期的真实波动率共5个指标作为各机器学习算法的输入,当期的波动率偏差作为输出,分别利用机器学习中的BP、SVR、RF及XGBoost算法对GARCH波动率模型的预测偏差进行训练,得到修正的偏差序列,将其与GARCH模型的预测值之和作为最终GARCH模型波动率的预测值,构建了基于机器学习偏差修正的GARCH波动率预测模型,主要流程如图4所示。

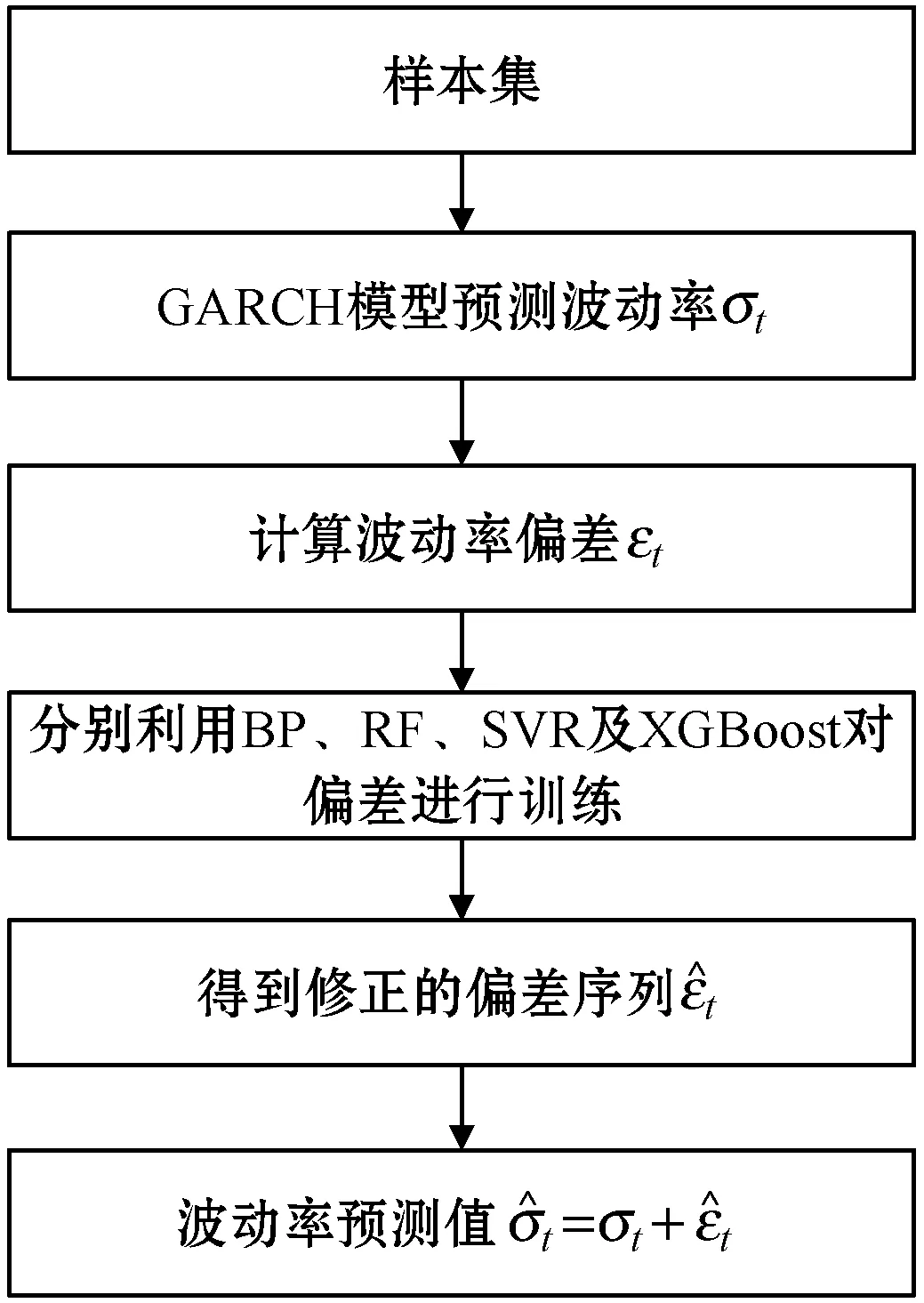
图4 波动率偏差修正预测模型

2 实证分析

2.1 数据描述性统计

为研究科创板设立对我国股市波动率带来的影响并对股市未来的波动率进行预测,本文以沪深300指数收益率为研究对象,沪深300指数综合了我国沪市和深市共300只股票,该指数能较为客观、全面地反映我国股市总体运行情况。由于我国在2019年6月13日正式设立科创板,因此在考虑数据的可比性和完整性以及真实性的基础上,选取2018年6月13日至2020年6月13日为样本区间,以科创板开板日期2019年6月13日为分界点,将数据分为科创板上市前和上市后两个部分,数据来源于CSMAR数据库。

表1为沪深300指数对数收益率的描述性统计分析。结果显示,对数收益率的均值为0,峰度系数大于3,且JB统计检验拒绝了服从正态分布的原假设。

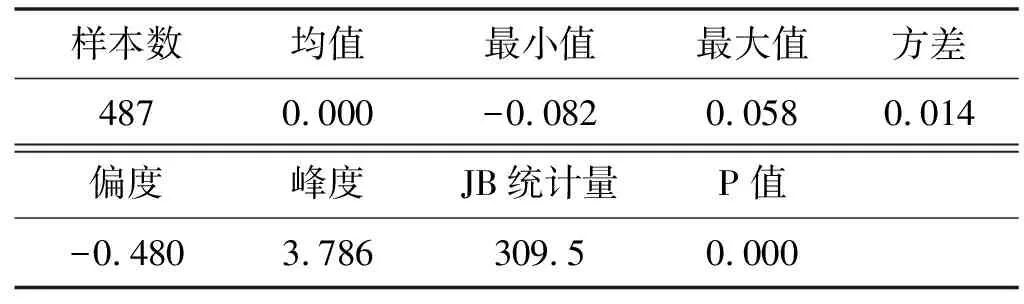
表1 沪深300描述性统计分析

图5与图6分别为沪深300指数收盘价与对数收益率时间序列图,可以看出对数收益率存在明显的波动聚集性,即一个大的波动后面总是跟着一个大的波动。初步可以判断该序列存在异方差性。

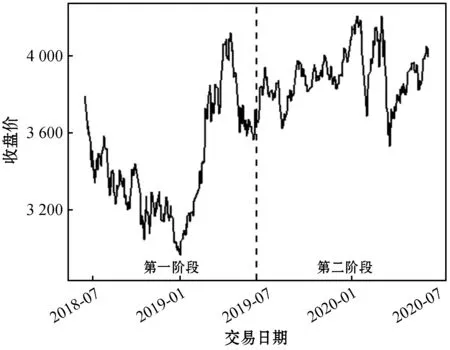
图5 沪深300指数收盘价走势图

图6 沪深300指数对数收益率走势图

2.2 时间序列统计分析

沪深300对数收益率的自相关与偏自相关图形如图7与图8所示,可以看出序列与滞后三阶数据间存在序列相关性。因此,需要建立ARMA(3,3)模型。

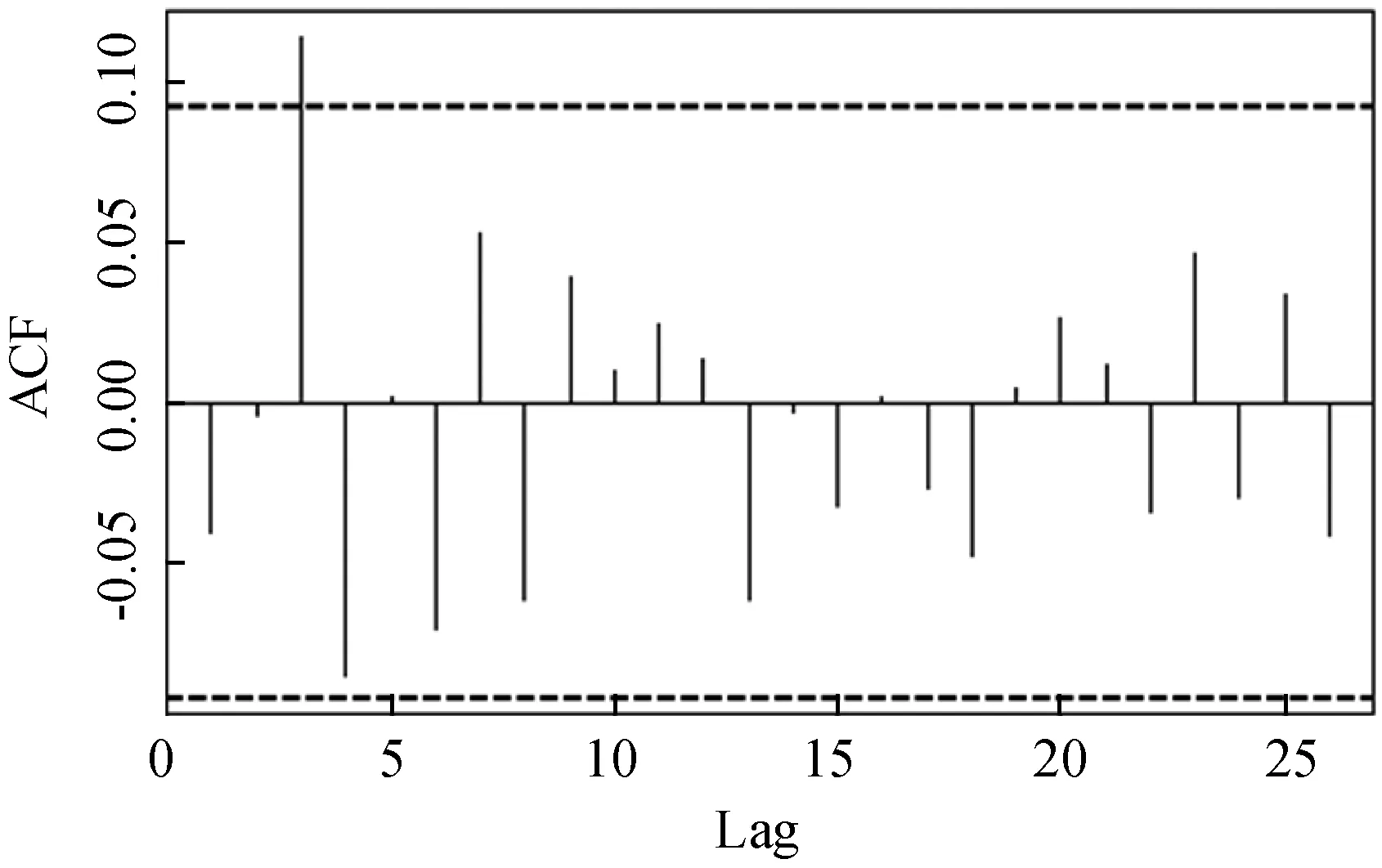
图7 沪深300指数对数收益率自相关系数图

图8 沪深300指数对数收益率偏自相关系数图

沪深300对数收益率ADF平稳性检验结果如表2所示,从结果可以看出对数收益率是平稳的,可以建立ARMA(3,3)时间序列模型。

表2 ADF平稳性检验结果

对ARMA(3,3)模型所得残差进行ARCH-LM检验,结果如表3所示。可以看出p值为0.048,在0.05的显著性水平下拒绝原序列不存在ARCH效应的假设。也就表明原始沪深300对数收益率存在ARCH效应。

表3 LM检验结果

2.3 带有外生变量的GARCH(1,1)模型估计结果

为了更加直观地刻画科创板的设立对股票市场波动性的影响,在模型中加入虚拟变量Di来引入科创板设立事件,科创板设立前虚拟变量赋值为0,科创板设立后虚拟变量赋值为1。本文分别建立了基于t分布、偏t分布及广义误差分布(GED)的GARCH模型。通过信息准则筛选后,最终选择GARCH(1,1)模型,具体方程如下:

(6)

各GARCH模型的系数如表4所示。可以看出,虚拟变量的系数小于0,说明科创板的上市对股市的波动起到了一定的抑制作用,但是系数很小,表明这种作用具有局限性。

表4 GARCH(1,1)模型结果

为了判断建立的GARCH(1,1)模型的有效性,本文基于t分布、偏t分布及GED对各模型的残差进行了Ljung-Box白噪声检验与ARCH效应检验,结果如表5所示。可以看出,各模型残差均不存在ARCH效应,说明建立的模型是有效的。

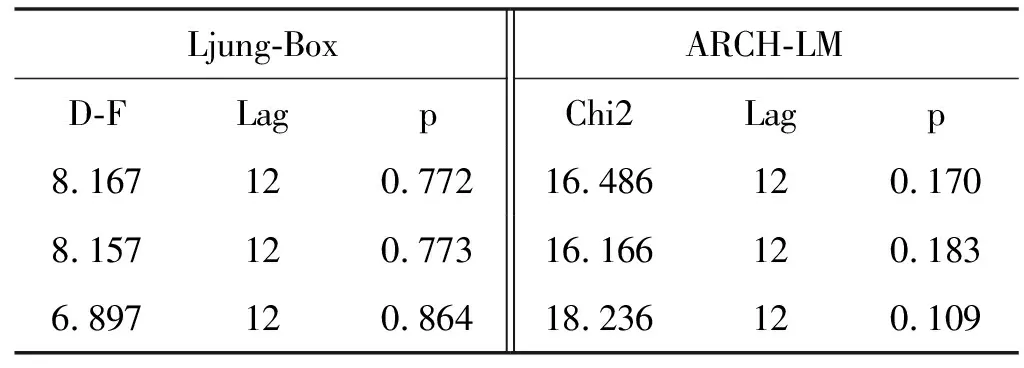
表5 Ljung-Box及ARCH-LM检验结果

2.4 波动率预测与评估

本文将样本集划分为训练集与测试集,采用滚动时间窗口的预测方法对模型进行预测。其中训练集为2020年1月15日(包括当天)之前共388个样本,测试集为2020年1月15日之后共97个样本。

实际波动率定义如下:

(7)

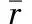
波动率偏差定义为GARCH模型预测的结果与真实波动率的差值,即:

εt=σt-RVt

(8)

通过计算各机器学习模型训练集与测试集RMSE、MAE及MAPE来比较各模型的优劣,各评价指标计算公式如下:

(9)

(10)

(11)

利用机器学习算法对GARCH模型的预测偏差进行训练,最终预测结果如表6所示。

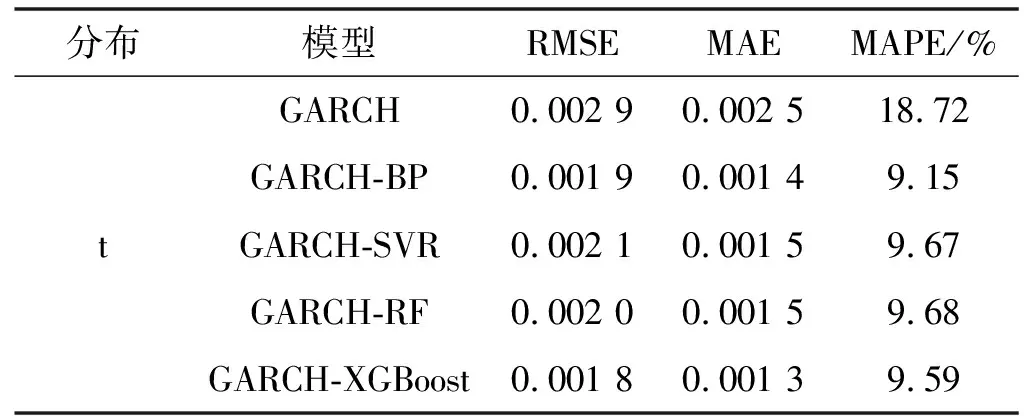
表6 各预测模型预测结果对比

可以看出,基于机器学习偏差校正的混合GARCH模型的预测精度普遍高于单一的GARCH模型。在学生t分布、偏t分布及广义误差分布中,基于XGBoost偏差修正的GARCH模型的预测效果均是最优。其中,学生t分布下的GARCH-XGBoost相比于GARCH模型的RMSE、MAE及MAPE值分别降低了37.93%、48%及48.77%。

3 结 语

波动率在金融衍生品定价、资产配置及风险管理等方面发挥着主体作用。随着全球金融市场一体化,对波动率的测度要求也在不断提高,因而构建合理的模型来测度金融资产的波动率,揭示金融市场波动的本质,对投资者和金融监管部门的风险管理具有重要的理论和实际价值。本文以沪深300指数收益率作为研究对象,研究了科创板的设立对股票市场波动性的影响,并提出了基于机器学习偏差校正的GARCH波动率预测模型,研究发现:

(1) 科创板的设立在一定程度上抑制了股票市场的波动,促进了股票市场的完善和稳定。但是虚拟变量系数值较小,表明科创板的设立对股票市场波动性的抑制作用是有限的,即其发挥的避险功能具有局限性。

(2) 在任一分布假设下,基于机器学习偏差校正的GARCH模型的预测精度明显优于单一的GARCH模型,在众多机器学习算法中,利用XGBoost对GARCH模型的偏差进行校正的预测效果最优。其中,与GARCH模型相比,学生t分布下的GARCH-XGBoost的RMSE、MAE及MAPE值分别降低了37.93%、48%及48.77%。