基于典型独立元分析方法的带钢热连轧过程故障检测

张瑞成 李禹亭 梁卫征 熊 伟

(华北理工大学电气工程学院 河北 唐山 063000)

0 引 言

随着科技的进步,现代工业的规模随之变大。一旦这些系统出现故障,将会造成财产损失,甚至是人员伤亡。所以,这些系统对安全性的要求越来越高,故障检测技术是阻止事故发生的重要手段。

在工业过程的故障检测中,多元统计方法因其不需要构建精确的模型而被广泛应用[1],主元分析方法[2-3](PCA)和核主元分析方法[4-5](KPCA)是效果比较好的方法,但是这两种方法求取控制限时的前提是观测数据服从高斯分布,然而大多数工业过程数据具有非高斯分布的特性,此时,PCA和KPCA的方法就不再适用。而独立成分分析[6-8](ICA)能够从工业过程数据中提取独立源,所以在工业过程中ICA具有更广泛的价值。然而,如果工业过程是动态过程时,ICA方法的检测效果也不是很理想。规范变量分析[9-10](CVA)是一种动态的子空间辨识方法,最初用于多变量分析中,它可以很好地处理自相关和互相关的问题,目前将CVA方法与故障检测结合起来的应用还比较少。带钢热连轧是一个复杂工业系统,这类系统一旦出现故障将会造成不可估计的损失,因此,对其进行故障监控和预测是不可或缺的步骤,Yin等[11]改进了标准偏最小二乘法并应用在了热轧机的故障检测中,Zhang等[12]将动态偏最小二乘法与独立成分分析法结合,应用于实际带钢热连轧过程中并取得了非常好的效果。

为了提高检测的准确率,将CVA和ICA的优势结合起来,并应用于带钢热连轧过程中,通过仿真实验,结果证明新方法具有更高的故障检测性能。

1 CVA和ICA理论分析

1.1 CVA理论分析

典型变量分析方法(CVA)是一种经典的子空间辨识方法,在最大化两组或更多组数据集之间的相关统计量的方面上是最有效的。假设动态系统的过程变量和质量变量之间的关系为线性时不变(LTI),并且具有过程噪声和测量噪声,可以简化为如下模型[13]:

(1)

式中:x(k)∈Rn表示n维状态向量;u(k)∈Rl表示过程变量;y(k)∈Rm表示质量向量;w(k)∈Rn和v(k)∈Rm代表过程及测量噪声;A、B、C、D为状态矩阵。

为了更好地分析系统,取任意时刻k为当前时刻,定义过去信息矩阵为:

(2)

定义现在和未来矩阵为:

(3)

式中:q为延迟时间数,主要取决于系统的阶次。yp(k)和yf(k)分别包含了过去和未来q个时刻测量的输出信息,定义N列Hankel矩阵[14]为:

(4)

(5)

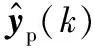
1.2 ICA理论分析

独立元分析方法主要分为源信号混合过程,观测信号预处理过程和解混过程,其中解混过程是工作重点。

传统ICA模型为:

x=As+e

(6)

式中:A∈Rm×n为未知的混合矩阵;x为m维观测变量矩阵;s为n维独立成分矩阵;e为残差矩阵。通常情况下,认为是理想环境,不存在噪声影响,模型可以简化成:

x=As

(7)

ICA的目的就是寻找一个分离矩阵W,使得:

(8)

能尽可能地接近源信号。ICA方法的基本原理如图1所示。

图1 ICA基本原理图

2 CV-ICA方法

CV-ICA故障检测方法,首先用CVA方法求取规范变量矩阵,然后对规范变量矩阵进行ICA分解,求出独立元,最后利用数据信息进行检测。该方法既可以通过解除相关性来提高检测的精度,同时适用于动态系统,还缩短了检测时间。

2.1 求取规范变量矩阵

当k=q+1时,式(4)和式(5)两个Hankel矩阵可以写为:

(9)

(10)

由此可以得出样本数n和延迟时间数q以及Hankel矩阵的列数N之间存在的关系:

N=n-2q+1

(11)

如果已知样本数n和延迟时间数q,可以由式(11)求出Hankel矩阵的列数N,构造Hankel矩阵,对应的协方差矩阵和互协方差矩阵分别为:

(12)

(13)

(14)

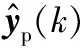
H=UΣVT

(15)

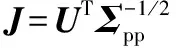
由此可以写出规范变量矩阵Z为:

(16)

在进行故障检测中,对于传统CVA可以建立以下监控统计量:

(17)

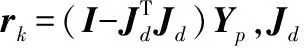
2.2 独立元分解及统计量构造

在得到典型变量矩阵Z之后,对其进行ICA分解,由式(7)和式(8)可以变形为:

Z=As

(18)

(19)

将式(16)代入式(19)可以得到独立元的估计量:

(20)

过去数据的估计量可以由下式计算:

(21)

同样,对于工业过程的故障检测,需要通过统计量来监控运行状况:

I2(i)=sT(i)·s(i)

(22)

(23)

采取KDE[15]的方法求取控制限,单变量核密度估计器的计算公式可写为:

(24)

式中:z为待估计的变量,zi为正常工况下的采样点,i=1,2,…,n,n为采样个数,K(·)表示核函数,一般选取高斯核函数,h是平滑因子。

实际上,I2和SPE统计量均为一维变量,所以,可以通过单变量核密度估计的方法得到统计量的概率分布,在置信度为α的情况下,大于α分为点即为统计量的阈值。

2.3 在线监控

(25)

计算在线采样下的独立元和输出估计量:

(26)

(27)

用以上方法求出监控统计量,判断是否超出控制限,若超出控制限,则有故障发生。

图2给出了基于CV-ICA方法的故障检测流程。

图2 CV-ICA方法的故障检测流程

3 仿真研究

为了验证CV-ICA方法的有效性,采用带钢热连轧过程案例对比各种方法的仿真进行研究。

带钢热连轧是一个极其复杂的动态工业过程,其设备工艺布置图如图3所示,可以看出,工业HSMP由6个子单元构成,包括:加热炉、粗轧机、热输出辊道和飞剪、精轧机、层流冷却和卷取机。在进行粗轧时,随着钢板厚度越来越薄,钢板长度会成比例地增加。在钢板通过辊道运输后,为了避免工作辊被损坏,飞剪对钢板的头部和尾部进行切割。然后,作为HSMP的核心步骤精轧过程,会进行更为精确的轧制,使得钢板的厚度进一步减小,以达到预期的厚度要求,这将作为故障检测的背景过程。随后,带钢经过层流冷却设备,最终卷成需要的产品。

图3 带钢热连轧过程工艺布置图

以某钢铁公司1 700 mm带钢热连轧生产线为背景,通过以上介绍的模型对现场采集的数据进行故障检测。7个机架的辊缝、轧制力和弯辊力(第一机架无弯辊力)作为过程变量,出口厚度作为质量变量,轧制过程中变量分配情况如表1所示。

表1 过程和质量变量分配表

仿真考虑的故障为第5机架的弯辊力采样值发生突变,是一种阶跃跳变故障。当该故障发生时,u18会突然增大,然后随着自动厚度控制的作用,后面两个机架弯辊力的值也会发生相应的变化,该故障会引起带钢板型的变化,是带钢过程中不希望发生的现象。故障从第5秒开始,持续10秒,在第15秒左右结束,采样间隔为10毫秒。

下面分别用CVA、ICA两种方法以及新提出的CV-ICA方法对此故障进行检测,图4和图5分别是用不同统计量对上述三种方法进行故障检测的结果。

(a) CVA

(a) CVA

图中实线部分是在线监控的统计量,虚线部分是通过KDE方法求得的控制限,如果统计量超出控制限,则判定有故障发生。

三种方法的漏检率和误报率的对比结果如表2所示。

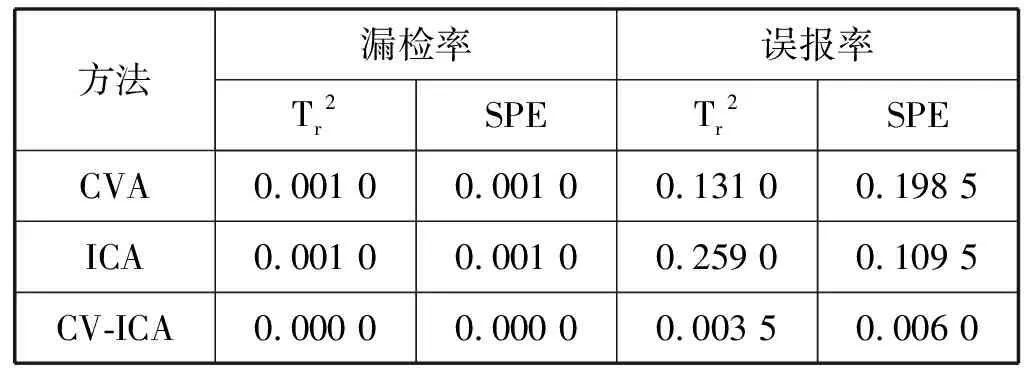
表2 故障漏检率和误报率对比结果

通过仿真结果可以看出,CVA、ICA、CV-ICA三种方法都可以在第5秒到第15秒给出明显的报警,漏检率非常小,但是CVA方法在前2秒、第15秒到第16秒、第21秒左右以及最后2秒的时候,本来没有故障发生,却出现了报警,故障检测的精度不足;ICA方法虽然同样可以检测出故障的发生,但是由于没有解除数据间的相关性,导致此方法在没有故障的时间段频繁出现报警,由此可见,传统ICA方法并不适用于复杂工业过程中的故障检测。

CV-ICA方法的检测结果相比于CVA和ICA两种方法有了明显的提高,不仅能够准确地检测出故障,而且有效地抑制了无故报警现象,降低了误报率,解除了数据间的相关性,仿真速度也有了一定的提高。

4 结 语

考虑到工业过程中大多数变量之间存在自相关和互相关的问题,提出了一种新的CV-ICA方法,并用带钢热连轧的精轧过程数据加以验证,由仿真结果可以得出以下结论:

1) 基于CV-ICA的方法可以有效地检测出带钢热连轧过程中的故障,检测率可达到100%。

2) 与传统的故障检测方法(CVA、ICA)相比,基于CV-ICA的方法大大降低了故障的误报率,由10%以上降到了0.6%以下。

3) 与ICA方法相比,基于CV-ICA的方法由于解除了原始数据的自相关和互相关性,仿真速度有了明显提高。