鲁棒优化配气理论研究

韩 璐,李军霆,李 汪,张艺铭

(西南石油大学电气信息学院,四川 成都610500)

1 引言

气举产油方式由于其工艺灵活,具有较强适应性,因而被国内外油气田广泛采用。陕西某油田于今年采用连续气举方式采油在初期取得了良好的效果。然而,由于井下油藏压力和油藏气液比存在扰动,产液量变化较大,同时,由于道路阻塞及停电等原因大幅降低了存储能力及产液处理能力,为防止扰动造成产液量超过单日上限,并在此基础上尽可能提升单日产量,需要合理的优化配气策略。

由于油田现场供气量有限,同时受压缩机功率、井身结构及经济效益等限制,无法使每一口井都获得最大产液量对应的注气量进行生产,因此需要通过优化配气理论对注入天然气进行合理分配以提高气举井组总产液量。针对该问题,大量学者对优化配气理论进行了深入研究,Mayhill[1]分析了连续气举井输入注气量和输出产液量之间的关系,提出采用二次函数拟合的“气举特性曲线”,但拟合精度相对较低;刘想平[2]提出了最大产液量模型、最大经济效益模型、最大化混合目标模型等三种优化配气模型;钟海全[3]等提出使用罚函数方法对优化配气模型求解,提高了求解精度,但实际结果与理论预测值间仍有较大误差;赵春立[4]等采用五次多项式拟合,并采用遗传算法求解,虽然拟合效果较好,但是高阶多项式的拟合需要采用专门软件,理论产量与实际产量间依然存在较大误差;苏博鹏[5]等提出在二次函数拟合的基础上采用增量注气方法求解,但该方法未考虑高次拟合下单井气举特性曲线可能出现的多驻点的情况;程功[6]等对三种已有优化配气数学模型进行了较为全面的求解。由于已有的研究均没有考虑扰动影响,实际产量和理论产量之间存在较大误差。

综上所述,现有研究均未考虑扰动存在且产液量受限情形下的优化配气问题。由于气举采油方式受扰动影响大,依据已有优化配气理论得到的优化配气策略的理论产量往往与实际产液量之间存在较大误差。历史数据显示,特殊工况下的实际产液量可能高于理论产液量14.2%,在产液量受限情形下将造成大量的资源浪费,因此需要充分考虑扰动对产液量的影响。本文在前人研究的基础上,充分考虑了扰动带来的不确定性,采用鲁棒优化理论,将已有优化配气模型与扰动模型相结合,提出了一种鲁棒优化配气方案,对扰动存在且产液量受限情形下的优化配气问题进行研究。

2 模型建立

2.1 优化配气理论标称模型量

假设油田某区块存在m口需要进行最优配气的气举井,m口气举井总产液量为Q0,设n为拟合多项式的最高次数,拟合多项式可采用cftool工具箱或者最小二乘法拟合得到,则最大化产液量目标函数可表示为以下形式

(1)

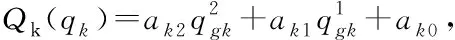
表1 15井气举特性曲线拟合方程表

该最大化产液量模型中,设各井的最小注气量为qgkmin,最大有效注气量为qgkmax,则各井的注气量范围约束条件为

qgkmin≤qgk≤qgkmax

(2)

(3)

由于油气田区块对生产油气的处理能力有限,因此还有区块总气体处理能力限制条件和区块总液体处理能力限制,分别表示为式(4)和式(5)

(4)

(5)

式中:GORk为第k口井的生产气液比;Dg为该区块的气体处理能力;DL为该区块的液体处理能力。

除上述约束条件以外,应根据现场实际需要增加u个确定性约束条件gv(v=1,2,…,u),约束条件gv将对最终优化配气策略产生影响。则最大化产液量模型可表达为

(6)

2.2 扰动模型

2.2.1 油藏压力扰动模型

通过对陕西某油田15口气举井历史数据的分析,并结合PIPESIM软件仿真,发现该油田影响气举井组产液量的主要影响因素为油藏压力扰动和油藏气液比扰动。为防止扰动造成日产液量超过上限,应充分考虑扰动对产液量的影响。

油藏压力受多种环境因素影响,如注水量、开采时间以及地层运动等,这些变化将直接导致产油量的变化,但是已有最大化产液量模型并没有考虑油藏压力扰动造成的影响,因此现有优化配气理论预测产量与实际产量之间往往存在较大误差。本文通过PIPESIM仿真,模拟油藏压力在(-100psi,100psi)之间变化,得到产液量变化量与油藏压力变化量的数据集。

以L7井为例,将该井相关数据输入PIPESIM,并仿真油藏压力在(-100psi,100psi)之间变化,将得到的数据与历史数据对比筛选后,通过cftool工具箱拟合,结果如图1所示。

图1 L7井油藏压力扰动拟合曲线图

由图1知,拟合优度为0.9995,说明该拟合符合客观规律,本文通过对15口气举井进行逐一仿真和拟合,15口井对一次函数的拟合优度如下表2所示。

表2 15口井油藏压力扰动模型拟合度

由表2可知,采用一次函数来拟合油藏压力在一定范围内的扰动是符合客观规律的,因此可以将油藏压力扰动拟合为以下形式

h(ξ)=cξ+d

(7)

式中:h(ξ)为扰动对应产液量,单位为stb,c、d为常数,ξ为油藏压力扰动量,单位为psi。

2.2.2 油藏气液比扰动模型

油田开采过程中由于注气压力、注气量、以及油气藏压力等变化的影响,不同时期开采时的油藏气液比会有扰动,这种扰动也会对气举井产液量造成一定影响。以L7井为例,通过PIPESIM模拟气液比在(-30 scf/stb,30 scf/stb)之间波动,将得到的数据集与历史数据对比筛选后,采用cftool采用拟合,其结果如图2所示。

图2 L7井油藏气液比扰动拟合曲线图

由图2可知,采用一次函数对一定范围内油藏气液比扰动和产液量进行拟合,其拟合优度为0.9895,因此,油藏气液比扰动模型可以采用一次函数拟。

通过对15口井进行PIPESIM仿真,各井的拟合优度如表3所示。

表3 15口井油藏压力扰动模型拟合度

由表3可知,采用一次函数拟合油藏气液比扰动模型拟合优度较高,由此得到油藏气液比扰动模型如下

l(η)=eη+f

(8)

式中:l(η)为油藏气液比扰动对应产液量,单位为stb,e、f为常数,η为油藏气液比扰动量,单位为scf/stb。

2.2.3 两种扰动模型有效性验证

为验证扰动模型的有效性,本文在已有最大化产液量优化配气模型中引入两种扰动模型,形成带扰动的最大化产液量优化配气模型

(9)

式中:ξkmin为油藏压力扰动最小值,ξkmax为油藏压力扰动最大值,ηkmin为油藏气液比扰动最小值,ηkmax为油藏气液比扰动最大值。

为验证扰动模型在任意扰动组合下对产液量的预测的准确性,采用PIPESIM分别对15口井随机产生一组已知且稳定的油藏压力扰动和油藏气液比扰动,并仿真各井在已知扰动下的产液量并与该模型预测产液量进行比较其结果如表4所示。

表4 引入扰动模型后各井误差对比表

由表4可知,由于已有优化配气方案并未考虑扰动带来的对产液量的影响,因此,一旦采油过程中出现了较大扰动,往往模型预测产液量与实际产液量之间会存在较大误差,而引入干扰模型后,可以大大减小对扰动量带来的产液量预测值与实际值之间的误差,实验证明在PIPESIM仿真下扰动模型有效。

2.3 鲁棒优化配气模型

2.3.1 两种扰动对应产液量的不确定性

由于受到油藏压力扰动和油藏气液比扰动的影响,井组的实际产液量与理论值误差较大。现场15口气举井的历史数据表明,特殊情形下实际产液量可能高于理论值14.2%,在产量受限情形下可能造成大量的资源浪费。而油藏压力扰动和油藏气液比扰动时刻存在且不断变化、难以测量,为防止扰动导致的产液量超过日产液处理能力上限,因此需要采用鲁棒优化的方法通过提高优化配气策略的鲁棒性以达到控制产量的目的。

油藏压力和油藏气液比由于受到人为注气、地下环境改变等因素影响而具有随机性的特点,本文考虑油藏压力扰动产液量和油藏气液比扰动产液量为如下形式

(10)

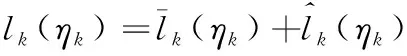
(11)

s.t.k(ξk)min≤k(ξk)≤k(ξk)max

(12)

s.t.k(ηk)min≤k(ηk)≤k(ηk)max

(13)

通过对15口井仿真,发现两种扰动之间的关联性较弱,假设参与优化配气的井数量为m,分别定义Δm、Δn为油藏压力扰动产液区间系数绝对值之和的上限值和油藏气液比扰动产液区间系数绝对值之和上限值,有Δm=Δn=m

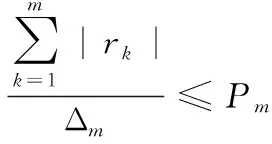
(14)

(15)

式中:Pm、Pn分别为油藏压力扰动不确定性预算和油藏气液比扰动不确定性预算,其取值代表了扰动量的不确定性程度。为方便计算,令ck=rk=sk,得Pm=Pn,令

(16)

2.3.2 鲁棒优化配气方案目标函数

对于含有不确定参数的最大化产液量鲁棒优化问题的目标函数,可描述为以下形式

(17)

(18)

(19)

(20)

式中:qgk为第k口井注气量,Qk为第k口井产液量,ξk0、ηk0分别为对现场第k口气举井油藏压力扰动和油藏气液比扰动的预估值。

(21)

2.3.3 约束条件

1)不同场景下单井注气量受地质环境、井身结构以及现场所能提供最大注气量等因素限制,应对各井注气量进行限制,对井k有

qgkmin≤qgk≤qgkmax

(22)

2)由于现场所能提供的注气量Qgt往往无法使所有气举井产液量达到最大,因此需要对所有气举井注气总量进行限制

(23)

3)考虑现场受到环境、交通以及停电等因素限制,产油处理能力DL下降,需重复分考虑不确定性扰动带来影响

(24)

4)由于受到现场天然气处理能力Dg限制,应满足

DL×GORk+Qgt≤Dg

(25)

3 模型求解

3.1 鲁棒优化对等式

求解鲁棒优化问题的核心思想是通过转化鲁棒优化模型中的不确定变量,使原来含有不确定性变量的模型转化为确定性模型,基于以上思想,本文采用线性优化鲁棒方法来对该鲁棒优化配气模型进行鲁棒优化对等式转换。

对式(24)变形得

(26)

即

(27)

根据线性对偶理论可得

(28)

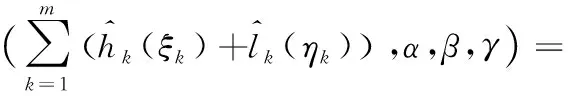
(29)

式中:α,β,γ均为拉格朗日系数。

(30)

将式(30)代入式(29),经过式(28)化简可得

(31)

综上所述,消去式(28)中的不确定性变量后,所得鲁棒优化对等式如下

(32)

至此,经过鲁棒对等式转换后,含不确定约束的鲁棒优化模型转化为了确定性模型,因此可以采用差分进化算法求解。

3.2 差分进化算法

3.2.1 差分进化算法原理简介

差分进化算法(Differential Evolution,DE)是一种具有鲁棒性强、原理简单、收敛快速、受控参数少等优势并且可用于求解确定性优化问题的全局优化算法。

差分算法程序流程图如图3所示。

图3 差分进化算法程序流程图

3.2.2 算例分析

设该油田15口气举井每日总产液量上限为18000stb/d,各气举井井底压力扰动范围均为(-100psi,100psi),油藏气液比扰动范围均为(-30scf/stb,30scf/stb),每日产气的处理能力上限为11.7mmscf/d,单日可用注气总量为4.5mmscf,单井的注气量下限为0.1mmscf/d,单井注气量上限为1.5 mmscf。采用PIPESIM仿真并在仿真过程中对各井随机生成油藏压力扰动和油藏气液比扰动。对该鲁棒优化问题建模并采用差分进化算法求解,求解结果如下表5所示。

表5 鲁棒优化方案与确定性优化配气量对比表

从表5中可以看出,常规确定性优化配气方案由于未考虑扰动带来的对产液量的影响,因此该方案的预测值与实际值之间差值较大,采用常规确定性优化配气方案将导致926stb的产液资源浪费。

4 结论

井组优化配气是所有气举井实现整体产量进一步合理提升与优化的重要手段。本文基于井底油藏压力扰动和油藏气液比扰动模型,使用鲁棒优化方法建立了鲁棒优化配气模型,算例分析结果验证了该方案的可行性。有以下几点结论:

1)油藏压力容易受到人为注气、注水以及各种自然条件变化的影响,而油藏压力和油藏气液比扰动对井组产液量有较大影响,本文将两种扰动建立的模型加入常规确定性优化配气模型中后,经过仿真验证,均能较大程度降低模型产液量预测值与实际值之间的误差,由此验证了两种扰动模型的合理性。