Timing and Single-pulse Study of Pulsar J1909+0122 Discovered by CRAFTS

Yutong Chen ,Pei Wang ,Di Li, ,Erbil Gügercinoğlu ,Rushuang Zhao, ,Lingqi Meng ,Jianping Yuan,Jiarui Niu,Weiwei Zhu,Yi Feng,Chenchen Miao,Chenhui Niu,7,Qingdong Wu,Na Wang,Shen Wang,Xiaoyao Xie,Mengyao Xue,Jumei Yao,Mao Yuan,Shanping You,Xuhong Yu,Youling Yue,Jie Zhang,Junshuo Zhang,Lei Zhang,Yabiao Wang0,Zhenye Gan0,Yuxi Li0,Zhongyi Sun0,and Chengjie Wang0

1 National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China;wangpei@nao.cas.cn

2 University of Chinese Academy of Sciences,Beijing 100049,China

3 Institute for Frontiers in Astronomy and Astrophysics,Beijing Normal University,Beijing 102206,China

4 Research Center for Intelligent Computing Platforms,Zhejiang Laboratory,Hangzhou 311100,China

5 Guizhou Normal University,Guiyang 550001,China

6 Xinjiang Astronomical Observatory,Chinese Academy of Sciences,Urumqi 830011,China

7 College of Physical Science and Technology,Central China Normal University,Wuhan 430079,China

8 Fudan University,Shanghai 200443,China

9 Qilu Normal University,Jinan 250200,China

10 Tencent Youtu Lab,Shanghai 200233,China

Abstract We report the discovery of PSR J1909+0122 by the Five-hundred-meter Aperture Spherical Radio Telescope(FAST)as part of the Commensal Radio Astronomy FAST Survey.PSR J1909+0122 has a spin period of 1.257 s and a dispersion measure of 186.2 pc cm−3.The averaged pulse profile shows two distinct components.We performed a single-pulse study based on a one-hour observation at 1.25 GHz on 2021 August 23.We used a threshold of 5σep to measure the nulling fraction(NF)as 63%±1.5%.The longitude-resolved fluctuation spectra and fast Fourier transform spectra of the binary sequences revealed the quasi-periodicity of nulling with a period of 30 rotation periods.We examined the reliability of the periodicity by comparing it to random noise injection.The NF,,and modulation periodicity PM of PSR J1909+0122 were compared with other periodic nulling pulsars,showing that the source of J1909+0122 has the second largest NF in the population.Long-term timing observations over six months were used to derive the phase-connected ephemeris of this pulsar.The measured P and values disfavor dipolar geometry for polar gap models,and the prediction for a space-charge-limited flow model in the case of inverse Compton scattering is only just above the death line.In this work,PSR J1909+0122 has revealed possible correlations between nulling behavior and pulsar properties,which will help to shed light on the pulsar emission mechanism and its temporal evolution in future observations.

Key words: (stars:) pulsars: general– (stars:) pulsars: individual (PSR J1909+0122)– stars: neutron

1.Introduction

Radio pulsars are known to exhibit multiple emission phenomena such as nulling (Backer 1970b),subpulse drifting(Drake &Craft 1968),and mode changing (Backer 1970a).Pulse nulling is the abrupt disappearance of emission from some pulsars for many rotation periods.The cessation of emission may occur over all frequencies (Ritchings 1976;Wang et al.2007) and last from one rotation period to months(e.g.,PSR B1931+24,Kramer et al.2006).The fraction of nulling pulses (nulling fraction,NF) could also range from essentially zero to over 90%.The NF is an important parameter for characterizing a nulling pulsar.It has been suggested that the NF is inversely correlated with the age of the pulsar(Ritchings 1976;Wang et al.2007).But pulsars with similar NFs can have quite different nulling behaviors (Gajjar et al.2012).

The nulling phenomenon was first discovered by Backer(1970b).There are two classes of models(Konar&Deka 2019)that explain this phenomenon—intrinsic and geometric.The intrinsic causes include,for example,the loss of the coherence conditions (Filippenko &Radhakrishnan 1982),changes in current flow in the magnetosphere (Timokhin 2010),an extreme case of mode changing (Esamdin et al.2005;Wang et al.2007;Timokhin 2010;Young et al.2014),etc.The transition between two states has been considered a random process for decades.Herfindal &Rankin (2007,hereafter HR07) first reported periodicity in the nulling of the bright Cambridge pulsar B1133+16,which had been the object of multiple studies.There were studies of PSR B1133+16 before HR07(Slee&Mulhall 1970;Taylor&Huguenin 1971;Backer 1973)that had noted a long-period modulation feature.But the periodicity was not revealed until HR07 “washed out”other factors that could affect the fluctuation spectrum by using an artificial pulse sequence in which they substituted the average profile for the profiles of the active pulses.With the cleaned data,a modulation period of 32 rotation periods was found.HR07 explained both the nulling phenomenon and its periodicity by the geometric effects mentioned above,where the line of sight passing between emitted sub-beams gives rise to “pseudo-nulls”.

More periodic nulling pulsars have been identified after HR07(Herfindal&Rankin 2009;Rankin&Wright 2008;Basu et al.2017,2018,2020a,2020b;Basu &Mitra 2019).There are 30 periodic nulling pulsars(Basu et al.2020b;Wang et al.2021b) out of over 140 nulling pulsars (Sheikh &MacDonald 2021) found so far.Basu et al.(2020b) made a detailed study of periodic modulation and found that subpulse drifting has a different relationship between the modulation period and spin-down energy loss than other periodic modulations.Meanwhile,many studies indicate that nulling,subpulse drifting,and mode changing may have a certain relationship.For example,Gajjar et al.(2017) found a unique nulling–drifting interaction in PSR J1840-0840,where the pulsar tends to shut down at the end of a drift band and to switch back to an emission phase at the beginning of a new drift band in both components.Wang et al.(2007) found a close relationship between nulling and mode changing,where the transitions between null and active states were associated with transitions between different modes.

The new pulsar J1909+0122 was discovered by the Fivehundred-meter Aperture Spherical Radio Telescope (FAST)during the Commensal Radio Astronomy FAST Survey(CRAFTS11http://crafts.bao.ac.cn/) drift-scan mode.It is a relatively slow pulsar with a period of 1.3 s.The dispersion measure(DM)is 186.2 pc cm−3.CRAFTS was designed to perform in drift-scan mode and to observe H I and pulsars simultaneously for optimal efficiency (Nan et al.2011;Li et al.2018,2019).To date,CRAFTS has discovered and confirmed 171 new pulsars(Qian et al.2019;Zhang et al.2019;Cameron et al.2020;Pan et al.2020;Cruces et al.2021;Wang et al.2021a,2021b;Tedila et al.2022;Wen et al.2022).The subsequent confirmatory observation,timing,and one-hour tracking observations of PSR J1909+0122 were also performed with FAST.

In this paper we report the discovery and analysis of PSR J1909+0122.In Section 2,we describe the observations and data reduction.Our analysis and results are presented in Section 3 including a single-pulse study and timing residuals.A discussion and a brief summary are given in Sections 4 and 5.

2.Observations and Data Reduction

Since FAST is the largest and most sensitive single-dish radio telescope,the CRAFTS pulsar search program performed with FAST is efficient due to its requirement of a relatively short integration time (Li et al.2018).PSR J1909+0122 was discovered in 2020 February using the CRAFTS drift-scan mode.It was then confirmed in 2021 July using FAST grid observations to locate its position.After the confirmation,we arranged 22 times of observations from 2021 August 18 to 2022 February 28 including a one-hour observation on 2021 August 23.All the observations were performed for pulsar timing,and the one-hour observation covering 2757 single pulses was used for single-pulse analysis.

The frequency range of all of our observations was 1000–1500 MHz,of which the effective band was 1050–1450 MHz due to the radio-frequency interference(RFI) and low response at the edges.The total number of channels was 4096,except for the observations on 2021 August 24,December 5,and 2022 January 27,which had 1024 channels.The data were recorded in tracking mode using the central beam of the FAST 19 beam receiver(Jiang et al.2020)with full-Stokes.Each time of observation started with a oneminute or two-minute calibration noise diode,depending on the duration of the observation,for calibration of polarization.

As a newly discovered pulsar,we had no ephemeris to fold the raw data.We processed the data of the confirmatory observation with the pulsar search and analysis software,PRESTO12https://github.com/scottransom/presto(Ransom 2011).After removing the RFI,we obtained an initial ephemeris with a given spin period (Pobs)and a dispersion measure (DM).We then used this ephemeris to fold the data from a one-hour observation on 2021 August 23.We determined a newPobsby aligning the peaks of single pulses at the same longitude and a new DM with the best signal-to-noise ratio (S/N).The new ephemeris was used to fold all the observations including the one-hour observation itself.

We folded the raw data using DSPSR13http://dspsr.sourceforge.net(van Straten et al.2011).The RFI was cleaned by both PAZ and PAZI programs from PSRCHIVE14http://psrchive.sourceforge.net(Hotan et al.2004).The times of arrival(ToAs) were obtained by PAT.

We used the one-hour observation on 2021 August 23 for the single-pulse analysis.Each spin period was divided into 2048 phase bins while folding.Calibration of polarization was performed using PAC from PSRCHIVE and the Stokes parameterIis used as intensity.

3.Data Analysis and Results

3.1.Nulling and Pulse Energy Distributions

Our single-pulse study is based on the one-hour observation covering 2757 spin periods on 2021 August 23.The “pulse stack,” i.e.,a sequence of consecutive single pulses,of PSR J1909+0122 is shown in Figure 1,along with the average profile in the lower panel and the relative energy variation in the left panel.The intensity of each period is normalized to the peak of the average profile.The profile has two well-separated components of which the leading one dominates and has higher intensity.Between these two components is a weak bridging region of emission.Along the pulse count axis,the nulling phenomenon is obvious and a quasi-periodicity could be detected by visual inspection.The periodicity is discussed in Section 4.4.

Figure 1.The main heat map shows the pulse stack of PSR J1909+0122 with intensity normalized to the peak of the average profile.The lower panel presents the profile averaged over all the pulses(red solid line)and a double-Gaussian fit to it(blue dashed line).The relative energy for each pulse is presented in the left panel.

We followed Kramer et al.(1994) to perform a double-Gaussian fit to the average profile.The Gaussian parameters were determined using the least-squares algorithm.The widths of the two components(w50),estimated by using the FWHM of the fitting Gaussian function,are 4°.15±0°.10 and 4°.92±0°.15 at the central frequency of 1250 MHz,respectively.The leading components have a somewhat sharper shape in most pulses while the trailing components are broader and have a lower flux peak.

The pulse energy distribution has been used to characterize the phenomenon of nulling (Ritchings 1976;Biggs 1992).We examined the energy distributions of the “on-pulse” and “offpulse” regions and both components.The on-pulse energy is the summed intensity of the on-pulse region extending from 3σ1(σ1was obtained from the Gaussian fit to the leading component) on the left of the first/leading Gaussian peak to 3σ2on the right of the second/trailing Gaussian peak.The offpulse window has the same length and is chosen from a region with a relatively stable baseline.The on-pulse and off-pulse energy histograms are shown in the left panel of Figure 2.The bimodal distribution shows that the on-pulse energy has a peak at zero,corresponding to null pulses,and another peak at about 2,due to the NF of about 60%.

Figure 2.(Left)Energy distribution for on-pulse(solid line)and off-pulse(dashed line)regions.〈E〉is the averaged on-pulse energy.(Right)The burst profile and null profile of PSR J1909+0122.There is no significant emission in the null profile.The amplitudes were normalized to the peak of the active profile.

Before estimating the energy distributions of both components,it is necessary to distinguish nulls from pulse-active or burst states.The histograms above give us only rough information and we need more details to identify individual nulls.We followed Bhattacharyya et al.(2010) and compared the on-pulse energy with a threshold based on the system noise level to identify a null.The uncertainty of the on-pulse energy is given by,wherenonis the number of onpulse bins and σoffis the rms of the off-pulse region.Given the high sensitivity of FAST,we chose 5×σepas the threshold.Pulses with on-pulse energy below this threshold were classified as null pulses.This definition was also used to identify null states of both components.We also confirmed that the threshold we used was appropriate by integrating active and null pulses.The profiles are shown in the right panel of Figure 2.There is no emission detected above our threshold within the integrated “null profile.”

According to the null-active sequence created above,the estimated NF is 63%±1.5%.The uncertainty of the NF is given by,wherenpis the number of nulling pulses andNis the total number of pulses (Wang et al.2007).

Single pulses were divided into four states also using the 5σepthreshold,where the on-pulse range was 3σ (σ was obtained from the Gaussian fit to the component)left and right of the peak of the component and σoffis the rms of the off-pulse region with the same length as the on-pulse region:active/burst state,null state,and single-component active states.Then we were able to determine the energy distributions for both components.The distributions are shown in Figure 3,where the total number of active pulses is 957 and 834 for the leading and trailing components,respectively.These results show that the first component has more active pulses and is concentrated in a more energetic region than the second component.

3.2.Nulling Behavior

3.2.1.Nulling Profiles and Duration

The transition patterns between two states can indicate the mechanism behind switches.For example,PSR B0818-41(Bhattacharyya et al.2010) was reported to have certain transition patterns while switching.The patterns in PSR J1727-2739 (Wen et al.2016;Rejep et al.2022) were more complicated,and there were both abrupt and gradual processes in the transitions.For our pulsar we also found different transition patterns,which are shown in Figure 4.This shows that a certain transition process is not always gradual or abrupt.

Figure 4.Relative energy vs.pulse number from pulses 1 to 100 and 400 to 440.The energy could rise or fall either abruptly or gradually.

We integrated the first active pulses(FAP)after null and the last active pulses (LAP) before null to compare with the average profile of all active pulses,since there are pulsars reported to have differences between these profiles(e.g.,Deich et al.1986;Gajjar et al.2014;Wen et al.2016;Rejep et al.2022).The three profiles are shown in Figure 5,all normalized with their own peak intensity.The leading component in all three profiles has a higher peak,and the peaks of the trailing component are 0.75,0.91,and 0.78 for the all-pulse profile,FAP,and LAP,respectively.So the differences are 0.25,0.09,and 0.22.As a reference,their baseline rms are 0.003,0.010,and 0.009.The FAP profile has two more equal components,while the all-pulse and LAP profiles have more similar leadingdominant profiles.The difference between the FAP and LAP profiles may indicate that the magnetosphere of the neutron star is under different conditions during these two processes.

Figure 5.Integrated profiles of all active pulses(black solid line),first active pulses(FAP,blue dashed line),and last active pulses(LAP,red dotted line).They were normalized to their own peak intensity.

Before further examining the quasi-periodicity indicated by the pulse stack,the distributions of null and burst durations are shown in Figure 6.According to the figure,both short bursts and nulls are most frequent.But besides the short lengths,there are visible concentrations of both distributions: the burst distribution has a not quite obvious peak around seven periods,and null lengths occur more frequently between 10 and 20 periods.This concentration may be the statistical origin of the periodic modulation of the nulling,while short nulls and bursts may play an important role in leading the periodicity to quasiperiodicity.

Figure 6.Histograms of burst duration(left panel)and null duration(right panel).The suspected peak of the burst duration distribution and the concentration area of null durations are marked.

3.2.2.Quasi-periodic Nulling

We first used the longitude-resolved fluctuation spectra(LRFS,Backer 1973) to estimate the significance of the periodicity.The integrated spectrum showed a peak around 30 rotation periods.However,this peak did not have a high S/N and could only be well distinguished from the noisy background by the smoothed line.Many factors,such as the variation of the pulse amplitude or giant pulses,can be the cause of this “white noise.” Our purpose is to eliminate all other effects and focus only on the nulling behavior itself.Herfindal&Rankin(2007)generated artificial pulse sequences by substituting the average profile for each active pulse to avoid effects caused by profile fluctuations.The integrated spectrum obtained from LRFS subsequently showed a more significant peak and less “white” fluctuation after this processing.

Here we used a more direct method to eliminate the interference.We generated a binary sequence where “0”represented nulls and “1” represented active pulses.This ensured that all subpulse information was washed away and the only possible periodicity was contained in the transitions between the two states (Basu et al.2017).We also generated similar sequences for both components to confirm that the periodicity of the single component and that of both components were consistent.

We then performed a fast Fourier transform (FFT) on the above binary sequences.The power spectra are shown in Figure 7,where the peak positions are 30±11,30±16,and 30±12 rotation periods for C1,C2,and both components,respectively.The positions were obtained by Gaussian fitting and the uncertainty was estimated from σ of the fit.These periods are in good agreement with each other and also with the period shown in LRFS as well.First,the same position of the three peaks shows that the periodicity is reliable,and second,the peaks at 30 rotation periods in spectra of binary sequences indicate that the low-frequency feature in LRFS is caused by nulling rather than subpulse drifting.

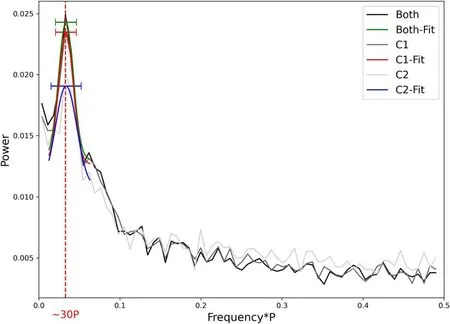
Figure 7.Nulling FFT spectrum of PSR J1909+0122,computed using binary sequences generated from pulses in null or active states.The green,red,and blue lines are Gaussian fits of the peaks of both components,C1,and C2,respectively.

A Fourier transform was also performed on shorter sequences to examine the time evolution of the periodicity.We used 256 points to compute a spectrum and then shifted the starting point also by 256 points each time.The result is shown in Figure 8.It can be seen that the brighter pixels,which represent the peaks of the spectra,are in a stable region as the starting number increases.Thus,the integrated spectrum in the lower panel therefore shows a peak at about 30 rotation periods,which coincides with the periods given in the LRFS and total nulling FFT spectrum.These aligned peaks imply that the nulling periodicity is time-invariant.

Figure 8.(Left) The time evolution of nulling FFT spectra of PSR J1909+0122.The peak of the spectra (upper panel) is at a stable position as the start number increases and leads to the peak in the integrated spectrum (lower left panel).(Right) Spectra computed from random data.The distribution intervals of null or burst duration are displayed in each subfigure.

We wondered whether the low-frequency feature in the FFT spectrum was caused by real periodicity,since it was not as strictly periodic as,for example,the rotational periodicity of the pulsar itself.Then we constructed test binary sequences that had the same length but randomly distributed nulling and burst duration.FFT was also performed on these sequences to check whether their spectra also had peaks,and the positions of the peaks if they did.Four spectra from our experiment are shown in the right panel of Figure 8.For each spectrum,the duration of the null or burst is evenly and randomly distributed in the interval given in the figure.It can be seen that as the distribution interval shrinks,the spectrum changes from a rednoise-like spectrum to a spectrum with a peak.However,even if the sum of the central values of nulling and burst duration is 30,the peak of the spectrum is not at exactly 30 rotation periods.On the one hand,our quasi-periodic nulling can be distinguished from a random process.On the other hand,if the spectrum of random data requires a relatively concentrated distribution interval to approximate our result,then the random sequence itself could be considered quasi-periodic.

3.3.Pulsar Timing Observations

To derive the time solution of PSR J1909+0122,more than six months of long-term timing observations were performed.For both high S/N and full data utilization,we integrated 100 spin periods and cross-correlated the integrated profile with the template for a ToA.The template used was the integrated profile of our longest observation on 2021 August 23.By visual inspection,we ensured that the profiles integrated over 100 periods were stable.We used the TEMPO215https://bitbucket.org/psrsoft/tempo2(Hobbs et al.2006)software to find the timing solution for the ToAs,which extend over 194 days.The timing residuals are shown in the left panel of Figure 9.This is obviously an isolated pulsar and can be modeled well with simple parameters.The timing parameters are given in Table 1.Three derived parameters are also presented: the pulsar’s characteristic age (τc=2),its surface magnetic field strength,and its rotational energy loss(=4π2I3whereI∼1045g cm2is the moment of inertia of the neutron star).

Table 1Parameters for PSR J1909+0122

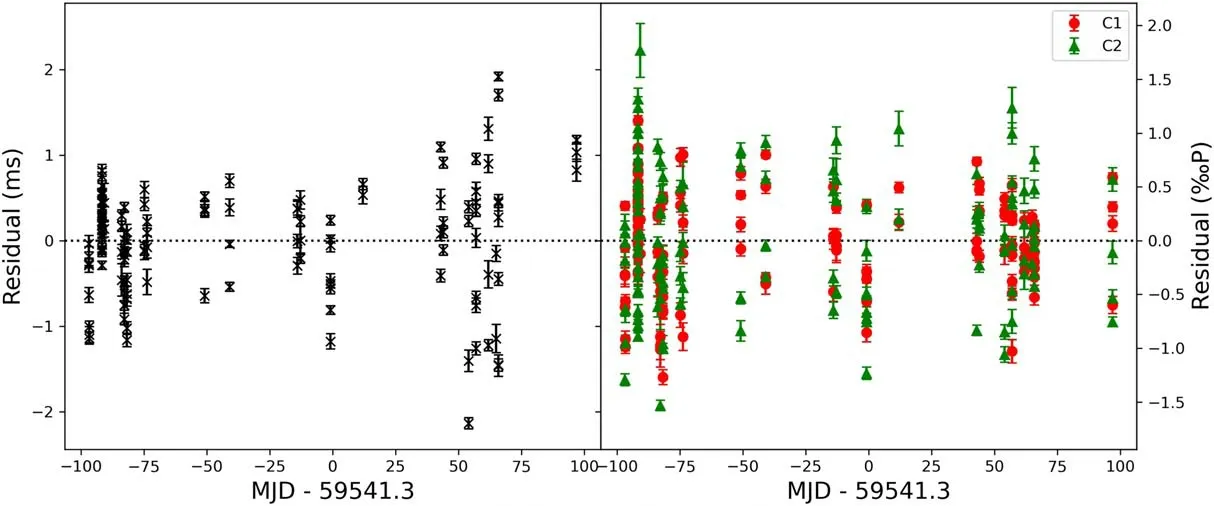
Figure 9.Timing residuals corresponding to 22 times of observations extending over 194 days.Residuals in the left panel were obtained by using average profile as a template.Residuals in the right panel were obtained by using C1-dominant (red circles) and C2-dominant (green triangles) templates.

Multicomponent pulsars can provide “single-componentdominant” templates for timing.Feng et al.(2021) divided single pulses into two types by comparing the intensity of their two components.Then they created two templates that had a larger leading component or a larger trailing component.They found that using different templates could not improve the rms residuals for the millisecond pulsar.We followed this process to see whether the same was true for slow pulsars.We averaged single pulses of each type to obtain two single-componentdominant templates for subsequent timing.The single-component timing residuals are shown in the right panel of Figure 9.As in Feng et al.(2021),the results were not improved by this method,where the rms of the left panel was 0.655 ms and the rms of the leading component(C1)and the trailing component(C2) were 0.581 ms and 0.764 ms,respectively,which means that timing with only the average profile is sufficient.

3.4.Mode Changing and Subpulse Drifting

As mentioned above,the low-frequency feature in the LRFS was proved to be generated by quasi-periodic zeroing.We found no other evidence for the occurrence of subpulse drifting.

To find a possible mode changing,we first assumed that the change was periodic,meaning that both modes had a certain length and repeated in turn.We defined a parameter to look for this,more specifically to look for two stable modes whose average profiles were exactly opposite in terms of the difference between their two component peaks.The difference between two components of an average profile was δp=(p1−p2)/(p1+p2),wherep1was the peak intensity of C1 or the leading component andp2was the peak intensity of C2.We changed three parameters to calculate δp: the sum of the lengths of two modeslsum,the length of one model1,and the starting period of this modePstart.Thelsumwe tried ranged from 10 to 200,l1ranged from 2 tolsum−2,andPstartranged from 1 tol1.Then we calculated the difference between δpof the average profiles of the two modes according to each set of parameters we chose.Unfortunately,we found that when the sum of the lengths of two modes was constant,when the difference between the δpof two modes was maximized,the length of one mode always minimized to two or three rotation periods.This tendency meant that the profile of the longer mode was exactly the average profile of all pulses,and the shorter mode,consisting of several pulses,happened to have an average profile with large δp.But these modes were not stable.As with the subpulse drifting,we found no evidence of mode changing and subpulse drifting above the 5σ level.

4.Discussion

We performed a one-hour tracking observation on 2021 August 23,and acquired 2757 single pulses for analysis.The average profile had two components,of which the leading component was dominant.The nulling phenomenon could be easily identified in the pulse stack,and the energy distribution of the on-pulse region further proved it.Due to the high sensitivity of FAST,instead of fitting the histogram of the energy distribution,we determined whether each individual pulse was null by using a threshold of 5σepto estimate the NF.The estimated NF was 63%±1.5%.We also determined the energy distributions of the two components,which did not match.

We integrated the FAP and LAP and compared them to the average profile.The profiles were all leading-componentdominant,while the profile of the FAP had a higher trailing component.The different patterns at the beginning and end of the nulling may indicate that the neutron star was in a different state during these processes.

Quasi-periodic nulling is the key feature of PSR J1909+0122.We first examined the distributions of nulling and burst duration.After statistical analysis of 36 pulsars,Basu et al.(2017) concluded that nulls of short duration (less than five periods)are dominant.The short nulls and bursts are also most common for PSR J1909+0122.But besides the short durations,both nulls and bursts have another clustering interval,which means that the distribution is not random.

The peaks of the LRFS and subsequent FFT spectra of binary sequences confirm the quasi-periodicity seen in the pulse stack.The estimated modulation period is (30±12)P.Spectra computed from double and single components suggest that the two differentially energy-distributed components behave similarly in terms of periodicity.The time evolution of the subspectra indicates that the periodicity does not vary with time.We noticed that several likely long-period pulsars(e.g.,Wang et al.2021c;Rejep et al.2022)were also calculated in this way.The spectra computed from these pulsars were not significant and the periodicity could not be confirmed.Then we wondered how much our result differed from random data.However,the spectra computed from random sequences did not agree with our result.

Basu et al.(2020b) made a detailed study of the periodic modulation of many pulsars,including 29 periodic nulling pulsars.A figure was displayed to show the relationship between the pulsars’spin-down energy loss and the modulation periods.Here we show a similar figure and introduce NF as a new parameter.In Figure 10 the red circle is PSR J1909+0122.On the one hand,PSR J1909+0122 is in the cluster in theversusPMfigure,which means that it is a typical periodic nulling pulsar.On the other hand,it has a relatively large NF.We chose,for example,a threshold of 40%to divide the points into two types.The upper left figure shows that pulsars with larger or smaller NF do not have different distributions.Considering that some of the samples were observed with lower sensitivity,which might ignore weak null emission,NF of these samples might decrease if the sensitivity of their observations is the same as that of PSR J1909+0122.Thus,PSR J1909+0122 is a high-NF example in the population of periodic nulling pulsars.

Figure 10.Modulation periodicities(PM),nulling fraction(NF),along with rotational energy loss().PSR J1909+0122 is the red circle,plotted along with the high-NF pulsars (blue triangles) and the low-NF pulsars (green squares).It is seen that J1909+0122 has typical PM and but large NF.

Sturrock (1971) predicts inefficiency of the generation of secondary plasma inside magnetospheres of long-period pulsars and in turn an increase in the nulling fraction as a pulsar ages.Since the polar cap shrinks with increasing period and age,the electron acceleration region marginally gives rise to pair creation instability.Hence,electron bunches responsible for coherent radio emission assume the form of thin arcs with a different viewing geometry,resulting in complex pulse morphology that differs from that of simple single pulses.In the carousel model of Ruderman &Sutherland (1975) the phenomenon of subpulse drift is attributed to the sparks ejected into the force-free magnetosphere and their circulatory motion with respect to the magnetic axis.The absence of subpulse features in PSR J1909+0122 is in agreement with a low rotational loss of ∼1031erg s−1of this star.In terms of the carousel model nulling is expected to be the dominant behavior in the pulsar radiation pattern afterP(the amount of spindown energy lost by the pulsar in one rotation period,1.57×1031erg for PSR J1909+0122) falls below ∼1030erg(Wright 2022).The duration of ≾30Pof nulls for PSR J1909+0122 implies either an unsteady inhomogeneous flow of particles into the emission region or a temporary global breakdown of the emission mechanism(Zhang et al.2007).We estimated the inclination angle α (the angle between the magnetic moment and rotation axis) of PSR J1909+0122 by fitting its position angle (PA) of linear polarization to the rotating vector model (Radhakrishnan &Cooke 1969).We used the Markov Chain Monte Carlo (MCMC) method based on the Python packages emcee (Foreman-Mackey et al.2013)and corner (Foreman-Mackey 2016) to obtain the geometrical parameters,which are shown in Figure 11.Both its position on theP−diagram and the low inferred value of the inclination angle suggest that PSR J1909+0122 evolves toward the socalled death valley,below which a pulsar is no longer energetic enough to generate radio emission (Chen &Ruderman 1993).The measured valuesP=1.27 s and=6.3×10−16s s−1disfavor dipolar geometry for polar gap models (Ruderman &Sutherland 1975),and the prediction for the space-chargelimited flow model(Arons&Scharlemann 1979)in the case of inverse Compton scattering is only barely above the death line(Zhang et al.2000).This observation supports the view that magnetic field structure above the polar cap may have multipolar structure or significantly curved geometry.For pulsars with ages greater than a few million years magnetic field evolution assisted by Hall drift distorts the dipolar field geometry and changes the polar cap structure (Geppert et al.2021).Hall drift along with the period lengthening–aging effect may be the underlying reason for the two-component pulse shape of comparable equivalent widths for PSR J1909+0122.The fact that old nulling pulsars occupy the same region on the−diagram as rotating radio transients(RRATs)suggests a causal evolutionary connection between them (Philippov &Kramer 2022).RRATs with observed periods in the range 41.5 ms to 7.7 s show a high degree of nulling,exceeding 95% (Abhishek et al.2022).Pulsars with nulling fractions less than 40% and those above this level constitute two statistically different classes (Konar &Deka 2019;Sheikh &MacDonald 2021).This apparent gap,if it is not a selection effect,may determine whether a long-period nulling pulsar will eventually evolve into an RRAT or not.Future observations of PSR J1909+0122 will reveal possible correlations between nulling behavior and other pulsar properties such as pulse morphology and allow for determination of the pulsar emission mechanism and its evolution with time.

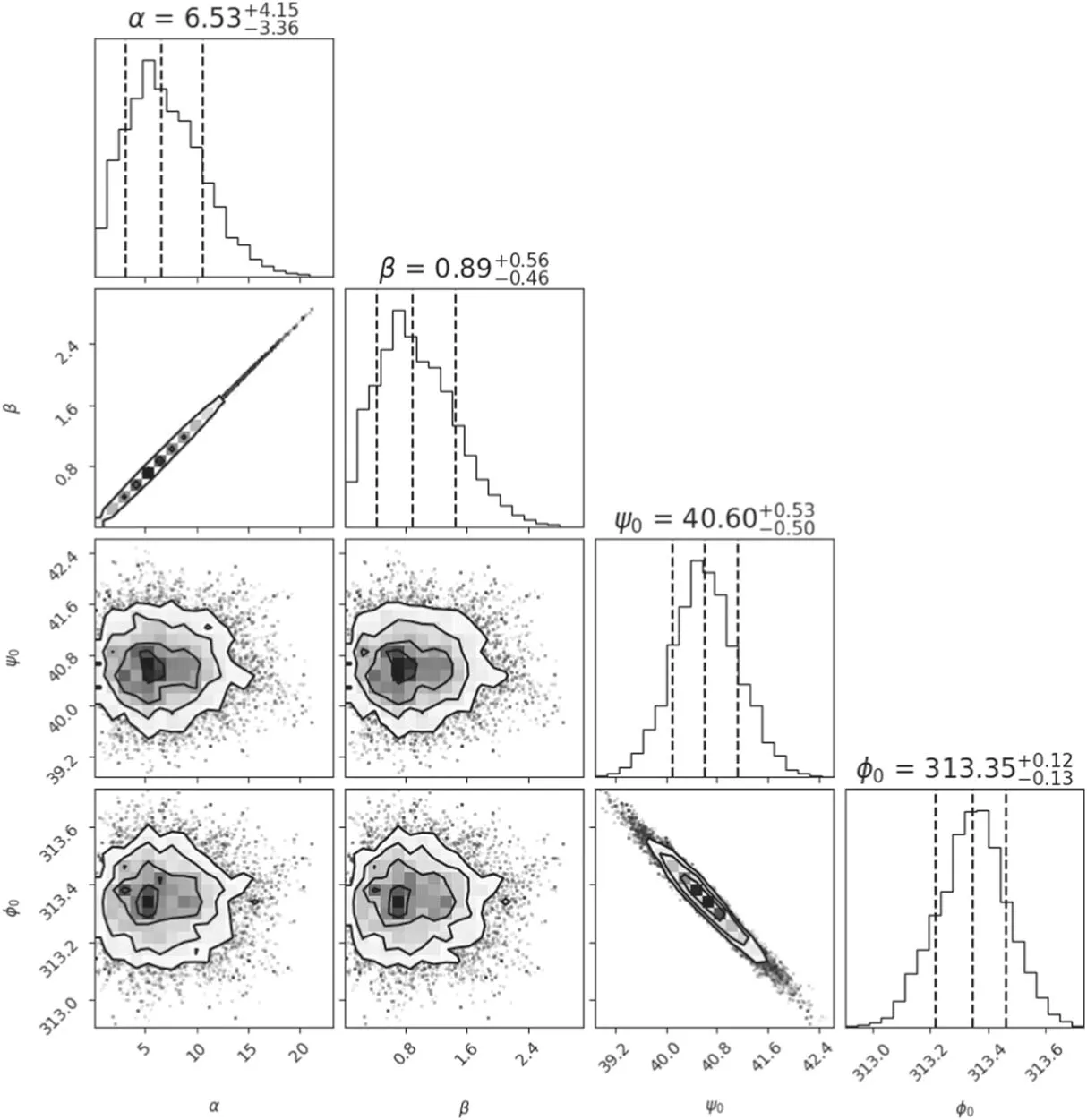
Figure 11.Posterior distributions of geometrical parameters α(magnetic inclination angle),β(angle between the line of sight and the center of the emission beam),Ψ0(value of PA when φ=φ0),and φ0 (pulse phase when PA changes most rapidly) by using the MCMC method.The dashed lines represent 16th,50th,and 84th percentiles in the corresponding histograms.

5.Summary

In this paper we report a new pulsar,PSR J1909+0122,discovered in the CRAFTS pulsar search program.

• The rotation period of PSR J1909+0122 is 1.257 s.The DM is 186.2 pc cm−3.

• We discovered the quasi-periodicity of the nulling phenomenon of J1909+0122 with a period of 30 rotation periods.

• We derived the phase-connected ephemeris of PSR J1909+0122 with rms of timing residuals=0.655 ms.Then we compared the rms of the single-component timing(RMSC1=0.581 ms,RMSC2=0.764 ms).The rms for both components was consistent and not improved compared to the average profile.

•=6.3×10−16s s−1together with the rotation period disfavors the polar gap models and the space-chargelimited flow model.The position of PSR J1909+0122 in theP−phase diagram demonstrates a possible connection between J1909+0122 and RRATs.

Acknowledgments

This work has used data from the Five-hundred-meter Aperture Spherical Radio Telescope (FAST).FAST is a Chinese national mega-science facility,operated by the National Astronomical Observatories of Chinese Academy of Sciences (NAOC).This work is supported by the National Natural Science Foundation of China (NSFC) Grant Nos.11988101,11725313 12041303,12041304,12203045,12203070,12103013,T2241020,and the National SKA Program of China (Nos.2020SKA0120200,2022SKA0130100,2022SKA0130104),the Foundation of Science and Technology of Guizhou Province (No.(2021)023),the Foundation of Guizhou Provincial Education Department (Nos.KY(2021)303,KY(2020)003).P.W.acknowledges support from the National Natural Science Foundation of China under grant U2031117,the Youth Innovation Promotion Association CAS (id.2021055),CAS Project for Young Scientists in Basic Research (grant YSBR-006)and the Cultivation Project for FAST Scientific Payoff and Research Achievement of CAMS-CAS.

ORCID iDs