Main Sequence Star Super-flare Frequency based on Entire Kepler Data

A.K.Althukairand D.Tsiklauri

1 Department of Physics and Astronomy,School of Physical and Chemical Sciences,Queen Mary University of London,Mile End Road,London,E1 4NS,United Kingdom;a.k.althukair@qmul.ac.uk,d.tsiklauri@qmul.ac.uk

2 Physics Department,College of Sciences,Princess Nourah Bint Abdulrahman University,Riyadh,PO Box 84428,Saudi Arabia

Abstract We wrote and used an automated flare detection Python script to search for super-flares on main sequence stars of types A,F,G,K and M in Kepler’s long-cadence data from Q0 to Q17.We studied the statistical properties of the occurrence rate of super-flares.For the G-type data set,we compared our results with the previous results of Okamoto et al.by splitting the data set into four rotational bands.We found similar power-law indices for the flare frequency distribution.Hence,we show that inclusion of a high-pass filter,sample biases,gyrochronology and completeness of flare detection is of no significance,as our results are similar to those of Okamoto et al.We estimated that a super-flare on G-type dwarfs with energy of 1035 erg occurs on a star once every 4360 yr.We found 4637 super-flares on 1896 G-type dwarfs.Moreover,we identified 321,1125,4538 and 5445 super-flares on 136,522,770 and 312 dwarfs of types A,F,K and M,respectively.We ascertained that the occurrence rate(dN/dE) of super-flares versus flare energy, E,shows a power-law distribution with dNdE ∝ E−α,where α ≃2.0 to 2.1 for the spectral types from F-type to M-type stars.In contrast,the obtained α ≃1.3 for A-type stars suggests that the flare conditions differ from those of the other spectral-type stars.We note an increase in flare incidence rate in F-type to M-type stars and a decrease in A-type to F-type stars.

Key words: Sun:flares–stars:flare–stars:solar-type–(stars:)starspots–stars:statistics–stars:rotation–stars:activity

1.Introduction

Flares are unpredictable events defined as a sudden,intense brightening caused by a large burst on the stellar surface as a result of magnetic energy release during the reconnection of twisted magnetic fields in the outer atmospheres of stars,which are typically located above or near starspots(Shibata&Magara 2011;Walkowicz et al.2011).Flares produce electromagnetic radiation with a wide range of wavelengths,from longwavelength radio waves to short-wavelength gamma-rays(Davenport 2016).

In general the importance of solar flares is due to their potential hazard to humankind,particularly damage to space technology such as satellites and terrestrial electrical power grids and pipelines via current surges generated by geomagnetic storms in the conductive layers of the Earth.Eastwood et al.(2017) consider an economic impact of space weather including solar flares.Schulte in den Bäumen et al.(2014)made an estimate for a 1989 Quebec-like event,that the global economic impact would range from 2.4–3.4 trillion dollars over a year.

However,the Sun is not the only star on which flares occur.Flares can arise in nearly all main sequence stars with exterior convective envelopes,including both cool and hot stars(Pettersen 1989),although they are more common in lowmass stars such as M dwarfs (Walkowicz et al.2011;Davenport 2016).Stellar flares are thought to be generated by the same process by which solar flares occur through magnetic reconnection (Davenport 2016).X-ray observations show that young stars can produce “super-flares” (Schaefer et al.2000),described as flares with radiative energy greater than 1033erg.These young stars rotate quickly,with rotational periods of only a few days.Even in their quiescent phase,fastrotating stars are strong X-ray sources,indicating a strong magnetic field and often showing large starspots(Pevtsov et al.2003;Cliver et al.2022).Thus,super-flares were thought impossible on the old,slow-rotating Sun.However,Schaefer et al.(2000) found nine super-flares with energies 1033–38erg in ordinary solar-type stars by analyzing previous astronomical data.White light flares are flares in the visible continuum(Namekata et al.2017).White light emission from a solar flare was first seen in 1859 (Carrington 1859;Pitkin et al.2014;Namekata et al.2017).Several studies of white-light flare observation were carried out by Mathioudakis et al.(2003,2006).

Due to the lack of spatial resolution on star surfaces,the study of stellar flares is limited to photometry or spectroscopy(Walkowicz et al.2011).Therefore,the Kepler mission made it possible to study stellar flares in detail(Van Doorsselaere et al.2017).Several studies have been conducted to analyze Kepler data and investigate stellar flares.The stellar rotation period,starspot area and flare energy can all be estimated using Kepler photometric observations (Cliver et al.2022).

Walkowicz et al.(2011) discovered 373 flaring stars on 23,000 cool dwarfs in the Kepler Quarter (Q)1 long cadence data using a new flare measure,the photometric equivalent width(EWphot),which expresses the flare energy relative to the star’s quiescent luminosity.Their findings suggest that M dwarfs flare more frequently but with shorter durations than K dwarfs and emit more energy.Pitkin et al.(2014) provided a Bayesian method for identifying stellar flares in light curve data.The approach is based on the general premise that flares have a distinct form,in which there is a sudden increase with a half Gaussian shape accompanied by an exponential decline.During 120 days of Kepler observations,Maehara et al.(2012)reported 365 super-flares on 148 solar-type stars (G-type main sequence stars).Shibayama et al.(2013) studied statistics of stellar super-flares.These authors discovered that for Sun-like stars (with surface temperature 5600-6000 K and slowly rotating witha period longer than 10 days),the occurrence rat e of super-flares with an energy of 1034–1035erg is once in 800–5000 yr.Shibayama et al.(2013) confirmed the previous results of Maehara et al.(2012)in that the occurrence rate(dN/dE) of super-flares versus flare energyEshows a power-law distribution with∝E−α,where α ∼2.Such occurrence rate distribution versus flare energy is roughly similar to that for solar flares.Kepler data were used to analyze 4944 super-flares observed on 77 G-type stars by Wu et al.(2015).They found that the power-law index γ of the frequency distribution of flares,as a function of their energy,is 2.04±0.17,consistent with previous studies.However,eight stars that flare frequently had γ values ranging from 1.59±0.06 to 2.11±0.19,suggesting that these stars may have different energy release processes.Moreover,they found that stars with shorter rotation periods tend to have larger γ values.Notsu et al.(2016) searched for super-flares on G-type main sequence stars and detected more than 1500 super-flares on 279 stars using long cadence data from Q0-Q6,and 187 super-flares on 23 stars using short cadence data from Q0-Q17.Their results show that the occurrence frequency of super-flares(d NdE) as a function of flare energy (E)follows a power-law function with an index of −1.5.According to their findings,the frequency of super-flares depends on rotation period,with the frequency showing an increase as the rotation period decreases.Yang et al.(2017)presented a study on 540 M dwarf stars that have exhibited flare events using Kepler long-cadence data.They examined the flare activity,normalized flare energy,chromosphere activity and starspot characteristics of M dwarf stars.They identified three phases of flare activity related to rotation periods and noted a steep rise in flare activity near M4.In addition,they found a positive correlation between starspot size and flare activity,as well as the power-law relationship between flare energy and chromospheric activity.Using Large Sky Area Multi-object Fiber Spectroscopic Telescope(LAMOST) Data Release (DR)5,and data from the Kepler and K2 missions,Lu et al.(2019) conducted a statistical study on M-type stars to investigate the relationship between chromospheric activity,flares and magnetic activity in relation to rotation periods.They found that the flare frequency is consistent with chromospheric activity indicators and that the equivalent widths of Hα and Ca II H have a significant statistical correlation with the flare amplitude.In addition,they confirmed that magnetic activity and rotation period have an effect on flares.The study also determined thresholds for flare time frequency based on specific values of Hα equivalent width and rotation period.Yang&Liu(2019a)detected 162,262 flare events on 3420 flaring stars among 200,000 Kepler targets using long cadence mode (LC) data from DR25.Notsu et al.(2019) used Gaia DR2 stellar radius estimates from Berger et al.(2018)and updated the parameters to study the statistical properties of Kepler solar-type super-flare stars first described in their previous studies (Maehara et al.2012,2015,2017;Notsu et al.2013;Shibayama et al.2013).Their findings indicate that more than 40% of the (279) solar-type (G-type main sequence) super-flare stars in Shibayama et al.(2013)were classified as subgiant.Old,slowly rotating Sun-like stars experience super-flares with energies 5×1034erg once every 2000–3000 yr,while young,fast-rotating stars manifest superflares with energies up to 1036erg.In addition,the maximum super-flare energy gradually decreases as the rotation period increases.Moreover,the maximum area of starspots in the early stages of a star’s life is independent of the rotation period.However,as the star ages and its rotation slows,the maximum area of starspots rapidly decreases at a certainProtvalue.Since the flare energy can be explained by the magnetic energy stored around starspots,these two declining trends are consistent(Notsu et al.2019).The most recent statistical analyses of super-flares on solar-type (G-type main sequence) stars using all of the Kepler primary mission data and the Gaia DR2 catalog have been reported by Okamoto et al.(2021).They developed an improved version of the flare-detection method in their previous studies (Maehara et al.2012,2015;Shibayama et al.2013),which involved the application of a high-pass filter to remove rotational variations caused by starspots.In addition,the sample biases on the frequency of super-flares were investigated,taking into consideration both gyrochronology and the completeness of the flare detection.They found 2341 super-flares on 265 solar-type stars and 26 on 15 Sun-like stars.It was estimated by Okamoto et al.(2021) that Sun-like stars with slow rotation could experience solar super-flares with energies of 1034erg once every ∼6000 yr.

Davenport (2016) reported the first automated search for stellar flares using the entire Kepler data set of DR24,including long and short cadence data.Approximately 3,144,487 light curves were analyzed for 207,617 distinct objects.Davenport(2016) identified 851,168 flares on 4041 stars and revealed a strong correlation between flares and the evolution of stellar dynamos as stars age by comparing the amount of activity of the flare with stellar rotation and the Rossby number.Using thresholds for the intensity increase,the increase in the running difference and the flare duration(Van Doorsselaere et al.2017)created a new technique for automated flare detection and applied it to Kepler’s long-cadence data in Q15.Out of the 188,837 stars in the Kepler field of view (FOV) during Q15,16,850 flares were found on 6662 of them.

The flare frequency distribution(FFD)is used to characterize flare energy and frequency,and it follows a power-law relation defined by∝E−α(Dennis 1985).The α index constrains the magnetic activity of various stars (Gao et al.2022).Flare completeness detection and precise energy calculation are crucial during fitting FFDs,as Gao et al.(2022) stated.They corrected the completeness of flare detection based on the data from Kepler and TESS,and reprocessed the light curve uniformly,correcting the detection efficiency for each star.They improved the completeness and accuracy of the energy calculation in flare detection by injection and recovery tests into each star’s original light curve for each flare event.

Kepler data analysis was not only limited to manual and automated methods;several studies have used machine learning to analyze Kepler data.Vida &Roettenbacher(2018) presented a machine learning-based code for detecting and studying flares.The code was evaluated on two targets for Kepler and Kepler’s second mission (K2) long and short cadence data,respectively.The detected flares for these two targets,as well as their energy,were found to be consistent with earlier findings.Breton et al.(2021) implemented a machine learning analysis pipeline to obtain rotation periods for Kepler targets.The algorithm was employed on K and M main sequence dwarfs studied in Santos et al.(2019),and the rotation periods of a sample of 21,707 stars were computed with an accuracy of 94.2%.Machine learning techniques were applied by Ofman et al.(2022) on the TESS data sets to discover exoplanet candidates,by using Kepler data of verified exoplanets as a part of the algorithm training stage and validation.Vasilyev et al.(2022) developed a new method for identifying the true flare sources using pixel-level data.This approach is helpful for automated flare detection.

The physical process that adequately describes solar flares is magnetic reconnection.These occur via a rapid change in connectivity of magnetic field lines,during which magnetic energy is converted into thermal energy (heating) and kinetic energy of plasma outflows.A general framework of solar flares is well accepted (Masuda et al.1994;Shibata et al.1995),however questions remain largely unanswered,such as:(i)how frequently and(ii)under what conditions do super-flares occur.

Our motivation is four-fold:

1.To study the statistics of stellar super-flares on main sequence G-type stars based on Kepler data in Q0–Q17,and compare our findings with those of Okamoto et al.(2021).

2.To examine the effect of not including (i) the high-pass filter and (ii) analysis of sample biases on the incidence rates of super-flares,(iii) gyrochronology and (iv) the completeness of the flare detection,considered by Okamoto et al.(2021) on our results.

3.To investigate how the flare statistics change on the timescale of 17 quarters.i.e.,what is the α power-law for data Q0 −Q6,Q7 −Q17 and Q0 −Q17.

4.To study the statistics of stellar super-flares on main sequence stars of other spectral types A,F,K and M.

5.To provide a Python script which finds super-flares automatically and only minimal human-eye analysis is needed.

Section 2 describes the Kepler spacecraft and its data.Section 3 presents the method used including the target selection,flare detection,rotation period determination and the flare energy estimation.Section 4 provides the main results of this study.In particular we first produce results for Q0-Q6,Q7-Q17 and Q0-Q17.Then we present a comparison with Okamoto et al.(2021).Finally,we report the results of other spectral types.Section 5 closes this work by providing our main conclusions.

2.Kepler Data

The Kepler spacecraft was launched in 2009 by NASA to search for exoplanets using the transit photometry method(Koch et al.2010).This spacecraft carried a photometer telescope with an aperture of a 0.95 m and 105◦2FOV and was designed to stare fixedly at one patch of sky in the constellations of Cygnus,Lyra and Draco,monitoring roughly 200,000 stars continuously,to detect changes in brightness caused by planets passing in front of the stellar disk(Shibayama et al.2013;Davenport 2016;Yang &Liu 2019b).The Kepler mission had two stages during its lifetime.Kepler’s primary mission(K1)which lasted for four years from 2009 to 2013 when the spacecraft lost two of the four reaction wheels on board.Thus,Kepler’s second mission(K2)started in 2014 and was carried out until 2018.Due to the problem with the telescope’s reaction wheels,it observed around the ecliptic plane.Targets were observed by Kepler using two cadence modes.The LC provided one photometric data point every 29.4 min,and the short cadence mode (SC) recorded one photometric data point every 1 min(Pitkin et al.2014).In order to make the Kepler solar panels always face the Sun,Kepler rotated every 90 days.Thus Kepler’s data were divided into almost 90-day quarters from Q0 to Q17 except for Q0,Q1,Q8 and Q17,which cover 9,33,67 and 32 days respectively.The observational periods with the start and end date of each quarter are shown in Table 1.

Table 1The Observational Period T and the Start and End Dates of Each Quarter

Since the luminosity loss caused by planetary transits is usually less than one hundredth of the star’s total brightness,Kepler is intended to obtain high-precision and long-period light curves of many stars(Shibayama et al.2013).As a result,Kepler is considered as a perfect platform to analyze stellar flares due to the significant sample size,the duration of the light curves and the photometric accuracy (Davenport 2016).

3.The Method

3.1.Target Selection

We carried out an automated search for super-flares on main sequence stars (type A,F,G,K and M) based on the entire Kepler data,using our bespoke Python script on long cadence data from DR25.The script can be found at (Althukair &Tsiklauri (2023),AFD.py,v1.0.0,Zenodo,https://zenodo.org/badge/latestdoi/578168613 doi:10.5281/zenodo.7755912,as developed on GitHub).The parameters for all targets observed by Kepler have been taken from the NASA Exoplanet Archive.The algorithm we used was based on the method of Maehara et al.(2012);Shibayama et al.(2013).All Kepler light curve data(2.5 TB) were obtained as fits files from the Mikulski Archive for Space Telescopes(MAST) with kind assistance by Deborah Kenny of STScI.Only long cadence targets were selected(with time resolution of 29.4 min).Since Kepler’s optical aperture has a radius of 4–7 pixels(Bryson et al.2010),and the pixel size of the CCDs is about four arcsec(Van Cleve&Caldwell 2009),it is thus quite possible that some targets are very close to each other on CCDs,which indicates that a nearby star’s brightness variations may influence the target star’s flux (Shibayama et al.2013;Yang et al.2017;Yang&Liu 2019b).Due to this reason we calculated the angular distance between every two stars in the entire sample,which is about 200,000 stars and excluded pairs of neighboring stars within 12〞 from the analysis,to avoid detecting fake flares on the target (Shibayama et al.2013).The overall number of samples that were excluded from the study according to this condition are about 6%.The angular distance θ between two stars was calculated by the following equation

where α1,α2,δ1,δ2are the right ascensions and declinations of the two stars in degree respectively.We used the Harvard spectral classification to obtain the spectral type for each target as shown in Table 2.Whereas the effective temperature and radius of main sequence stars in different spectral types are as follows: 2400 K ≤Teff<3700 K and radius ≤0.7R⊙for M-type,and 3700 K ≤Teff<5200 K and radius of 0.7–0.96R⊙for K-type,for G-type we used the same effective temperature of Maehara et al.(2012);Shibayama et al.(2013)which ranges between 5100 K ≤Teff<6000 K and radius of 0.9–1.15R⊙,F-type has 6000 K ≤Teff<7500 K and radius range between 1.15–1.4R⊙,and A-type has 7500 K ≤Teff<10,000 K and radius between 1.4 −1.8R⊙.Due to the small number of A-type main sequence stars that fall under these conditions,which makes the statistics inaccurate,we have not implemented radius restrictions for this spectral type.The total number of main sequence stars is 2222,10307,25442,10898 and 2653 for M-,K-,G-,F-and A-type,respectively.

Table 2The Effective Temperature Teff,Radius and Number of Stars for Each Spectral Class

3.2.Flare Detection Method

Kepler light curves contain two kinds of flux,the Simple Aperture Photometry (SAP) flux and the Pre–searched Conditioning SAP(PDCSAP)flux,which has long term trends removed (Davenport 2016).Figure 1 illustrates the difference between these two types of fluxes.All light curves were analyzed using an algorithm with a similar technique to Maehara et al.(2012),Shibayama et al.(2013).

Figure 1.Light curve of KIC 9146690 using two types of flux.The SAP flux(blue) and the PDCSAP flux (red) which detrends the time variation.

A brief description of this method is as follows.In order to be statistically accurate,after generating light curves of all selected stars using the PDCSAP flux,we computed the distributions of brightness variation by calculating the flux difference in adjacent time intervals between every two neighboring points of all the data points in the light curve.The purpose of this step,as clarified by Shibayama et al.(2013),is to avoid false flare detection and misdetection of short stellar brightness variation and not to miss large flares.Then,we find such value of flux difference where the area under the distribution is equal to 1% of the entire area.This value indicates a large flux difference between two adjacent points.To enhance the threshold,we multiplied the 1% value of the area by a factor of three.This threshold value has been chosen by Shibayama et al.(2013) based on multiple tests.Examples of some of the outputs of this method,which give the distribution of brightness variations and the threshold determination,are displayed in Figure 2.Figure 2(a) and 2(d) depict light curves of KIC 4371489 at Q2 with a rotation period of 1.09 days and KIC 7354508 at Q3 with a rotation period of 17.8 days,respectively.Figure 2(b)and 2(e)feature a zoom-in of these light curves,illustrating the rotational periods.Figure 2(c) and 2(f) show the distribution of brightness difference between every two neighboring points of all the data points in the light curves of KIC 4371489 and KIC 7354508,respectively.The dashed vertical lines indicate 1% of the total area under the distribution curves.The solid vertical lines indicate the threshold values of flare detection,which is equal to three times 1% of the area under the curve.According to Shibayama et al.(2013),the detection threshold depends on the star’s rotational period,and its brightness variation amplitude.For short-rotation-period stars (e.g.,KIC 4371489),the distribution of brightness variations appears to extend larger than that for long-rotation-period stars (e.g.,KIC 7354508).This large extension is because the difference in brightness between two successive data points is greater in stars with short rotation periods than in stars with long rotation periods,resulting in a greater value of flare detection threshold.Also,thresholds in stars with large brightness variation amplitudes are larger than those in stars with small brightness variation amplitudes.We defined the start time of a flare as the time when the flux difference of two consecutive points exceeds the threshold for the first time.

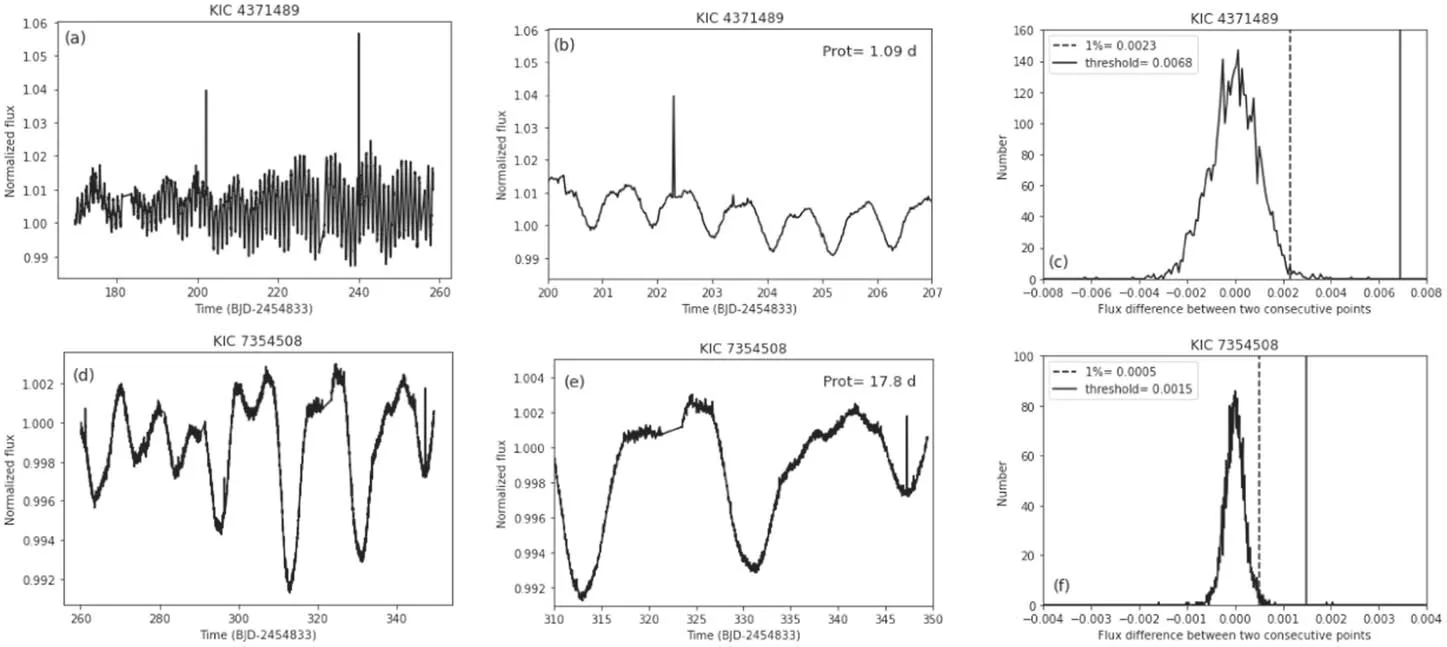
Figure 2.Illustrations of flare detection method used by Shibayama et al.(2013) in both fast and slowly rotating stars.(a) and (d) display the light curve of KIC 4371489 and KIC 7354508 respectively.(b)A zoom-in into the light curve of KIC 4371489 showing a rotation period of 1.09 days.(e)A zoom-in into the light curve of KIC 7354508 displaying a rotation period of 17.8 days.(c)and(f)depict the distributions of brightness variation between every two neighboring points of all the data points in the light curves of KIC 4371489 and KIC 7354508 respectively.The dashed vertical lines signify the value of 1%of the total area under the curve,and the solid vertical lines mean the flare detection threshold.

To determine the flare end time,we computed the three standard deviations(3σ)of the brightness variation distribution.We used the relative flux (ΔF/Favg) as shown in Figure 3,where ΔF=Fnorm(t)−Favg,withFnorm(t) being the normalized flux of the light curve andFavgthe normalized flux average,and fitted a B-spline curve through three points distributed around the flare.Each of these three points is an average of five data points distributed as follows: the first average point is just before the flare,the second average point is around 5 hours after the flare maximum and the third average point is around 8 hours after the flare maximum,see Figure 3(b).The purpose of curve fitting is to remove long-term brightness variations around the flare (Shibayama et al.2013).After subtracting the B-spline curve from the original relative flux as in Figure 3(c),we define the end time of the flare as the time when the relative flux produced by the subtraction becomes less than the value of 3σ of the distribution for the first time.The flare amplitude is given by

Figure 3.Demonstration of the removal of long-term brightness variations around the flare.(a)Part of KIC 7958049 light curve around the flaring time(10 days of observation).(b)Fitting a B-spline curve(dashed curve)through three points around the flare(squares).The first point is an average of five data points just before the flare,the second point is an average of five data points 5 hr after the peak and the third point is an average of five data points 8 hr after the peak.All three averages are shown as squares.Note that the flux is normalized by the flux just before the flare F◦.(c) The produced light curve after subtracting the B-spline curve from the relative flux.

whereFmaxis the normalized flux at the flare peak,andFavg2is the normalized flux average of two points distributed around the flare.The first is the average of five data points before the start of the flare and the second is the average of five data points after the end of the flare;Favgis the normalized flux average.

After selecting the start and end time of each flare,we applied conditions to all flare candidates.These conditions are as follows: the duration of the flare should be longer than 0.05 days,equaling 72 minutes,which means at least three data points,and the period of the decline phase of the flare should be longer than the period of the increase phase.Only flare events that satisfy these conditions were analyzed (Shibayama et al.2013).After selecting all flares that met the conditions,we checked by eye the light curve for each flare and eliminated false flares.We have not tested the pixel level data of stars showing flares as done in Shibayama et al.(2013) for the reason of simplicity.As can be seen in our results,this test omission does not alter overall findings about,e.g.,flare occurrence rate which we found to be similar to Shibayama et al.(2013).

3.3.Rotational Period Determination

We computed the brightness variation periods of light curves using the Lomb-Scargle periodogram,a common statistical method for identifying and describing periodic signals in unevenly sampled data (VanderPlas 2018).We set the oversampling factor (number of samples per peak) in the periodogram to be five (VanderPlas 2018) and created a Lomb-Scargle periodogram for each light curve in each quarter from Q2 to Q16 using PDCSAP flux.The light curve data of Q0,Q1 and Q17 were excluded due to their short duration,similar to McQuillan et al.(2014),as shown in Table 1.Further,we assigned the period corresponding to the highest power of the periodogram to be the rotation period for the Kepler ID in a certain quarter.To make the selection of star rotation period automatic rather than manual,we calculated this value with an accuracy of a day without the decimal part since fraction of a day would not significantly affect the results.For periods of less than a day,we set them to 0.5 days,and for periods of less than 0.1 days,we excluded them.According to McQuillan et al.(2014),a good sign of actual astrophysical periodicity is that it can be found in different parts of the light curve.This is because peaks caused by systematics or artifacts are less likely to appear in multiple regions of the light curve.Therefore,in order to choose the accurate rotational period,we selected the period that is most frequent in all quarters from Q2 to Q16 for each Kepler ID.We then require that the period chosen for all quarters should be identified in at least two distinct segments,following the McQuillan et al.(2014) technique,where the segment is defined as three consecutive Kepler quarters (Q2,Q3,Q4)–(Q5,Q6,Q7)–(Q8,Q9,Q10)–(Q11,Q12,Q13)–(Q14,Q15,Q16).It is worth noting that this method has only been applied to the 1897 Kepler IDs with super-flares that will be considered in 4.1.3.Using the segments technique,we determined the rotation periods of 548 flaring stars in the Kepler sample.In addition,we derived 222 rotation periods based on our most frequent period in all quarters.These selected periods showed significant correlation with those published in previous works.We used Excel’s (CORREL) function to calculate the correlation coefficient.The correlation coefficient reaches about 0.99 for seven IDs in Yang &Liu (2019b),0.99 for 70 IDs in Santos et al.(2021),0.97 for 54 IDs in McQuillan et al.(2014),0.95 for 54 IDs in Reinhold &Gizon (2015) and 0.92 for 20 IDs in Nielsen et al.(2013).After comparing the 770 rotation periods that we obtained from both approaches to those periods reported in McQuillan et al.(2014),we found 434 common IDs with a correlation coefficient of 0.85 between their periods.Moreover,231 common IDs in Nielsen et al.(2013) had a correlation coefficient of 0.94 between their rotation periods.Plots of these correlations are shown in Figure 4,where we used theregplotfunction in the Seaborn Python library to plot the linear regression model fit to the data.Thex-axis in both figures represents the rotation periods obtained by this study.They-axis corresponds to the periods of rotation published by McQuillan et al.(2014) in 4(a) and Nielsen et al.(2013) in 4(b).In both figures,variables change in the same direction,indicating a significant positive correlation.The rotation periods of 80 stars were obtained from other works,including 67 from McQuillan et al.(2014),6 from Reinhold &Gizon (2015) and 7 from Santos et al.(2021),while we found that 1047 stars have no discernible rotation period.This could be due to three reasons as mentioned by Yang et al.(2017):(i)the rotation period is longer than 90 days(a quarter),which makes it difficult(or impossible)to detect them in the star’s frequency spectrum;(ii) at the accuracy level of Kepler,the light curve has a small amplitude due to the inclination angle and low activity level;(iii) fastrotating stars have spots at the poles(Schüssler&Solanki 1992),making detecting light variation through rotation hard.The entire results on rotational period determination can be found at https://github.com/akthukair/AFD.

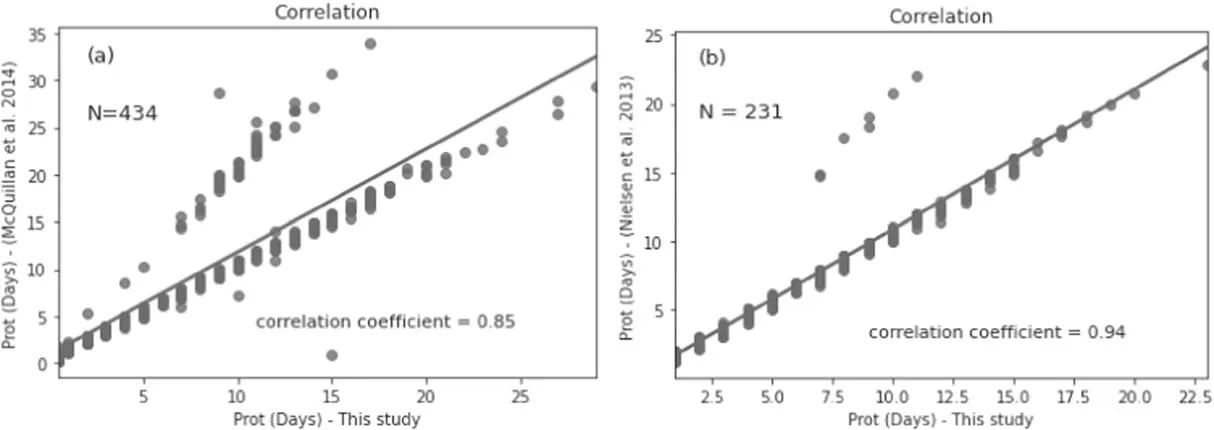
Figure 4.The comparisons of the periods determined in this study to those detected by McQuillan et al.(2014)and Nielsen et al.(2013)in(a)and(b),respectively,reveal a strong positive correlation in which both variables vary in the same direction.The x-axis shows the rotation periods found by this study,and the y-axis displays the rotational periods provided by McQuillan et al.(2014) and Nielsen et al.(2013).N represents the number of stars in each comparison.The correlation coefficient between our periods and McQuillan et al.(2014) is 0.85,while it is 0.94 for Nielsen et al.(2013).

3.4.Flare Energy Estimation

We determined the total energy of each flare from the star luminosity,flare amplitude and its duration,following Shibayama et al.(2013;Yang et al.(2017).

The star luminosityLstar,which is the total energy that a star produces in one second,depends on the radius of the starRand the surface temperatureTeff.This is given by the equation

where σSBis the Stefan–Boltzmann constant,and 4πR2is the entire surface area of the star.Hawley &Fisher (1992),Kretzschmar (2011) found that the continuum emission released by a white-light flare is compatible with blackbody radiation at about 9000 K.Therefore,in this studyTflareis assumed to be 9000 K according to Shibayama et al.(2013),Yang et al.(2017),Günther et al.(2020)and the luminosity for a blackbody emitting star is expressed as

HereAflareis the area of the flare and can be estimated by the equation

whereCflareis the flare amplitude for the relative flux,andRλis the response function of the Kepler instrument (Caldwell et al.2010).The photometer in Kepler uses one broad bandpass ranging from 420 to 900 nm.Bλ(T) is the Plank function at a given wavelength and it is expressed as

wherehis Planck’s constant,cis the speed of light,Tis the temperature of the blackbody andkis Boltzmann’s constant.

Lflarecan be calculated by substituting Equation(5)into(4).SinceCflare(t)is a function of time,Lflare(t)is also a function of time.Therefore,the total energy of the flare is the integral ofLflareover the flare duration,and is written as

4.The Results

This section presents the main results of this study.

4.1.Super-Flares on G-type Dwarfs

4.1.1.Super-Flares on G-type Dwarfs in Q0-Q6

During 494 days of continuous observation of 25,440 G-type dwarfs,searching for super-flares using Kepler long cadence data,we found 1298 super-flares on 588 G-type dwarfs.Among them,229 super-flares were identified on 132 slowly rotating stars.As for the Sun-like stars,which are known as stars with a surface temperature of 5600 K ≤Teff<6000 K,a surface gravity ofglog 4.0>and a rotational period exceeding ten days (Shibayama et al.2013),we found 151 super-flares on 93 Sun-like stars.The number of detected super-flares in this study is less by 16% than the 1547 superflares found in Shibayama et al.(2013).In contrast,the number of super-flare stars in this study is approximately 2 times the 279 super-flare stars in Shibayama et al.(2013).Since interstellar activity varies,some stars have manifested more than one super-flare,while others have shown only one.In comparison,we found that 161 stars out of 588 experienced more than one super-flare,while 427 stars underwent only one super-flare.The number of Sun-like stars that exhibit more than one super-flare is 18 out of 93,while 75 Sun-like stars manifested only one super-flare.The most energetic super-flare found had an energy of 2.94×1036erg,an amplitude of 0.35 and lasted for about 0.08 days.Figure 5 depicts four light curves with a 30-day observation period of the most energetic super-flares that we found with their Kepler ID (left panels).The right panels display a zoom-in of these super-flares,showing their respective energy and their peak time.The black squares on the light curves indicate the data points of the superflare from the time it starts until it ends.

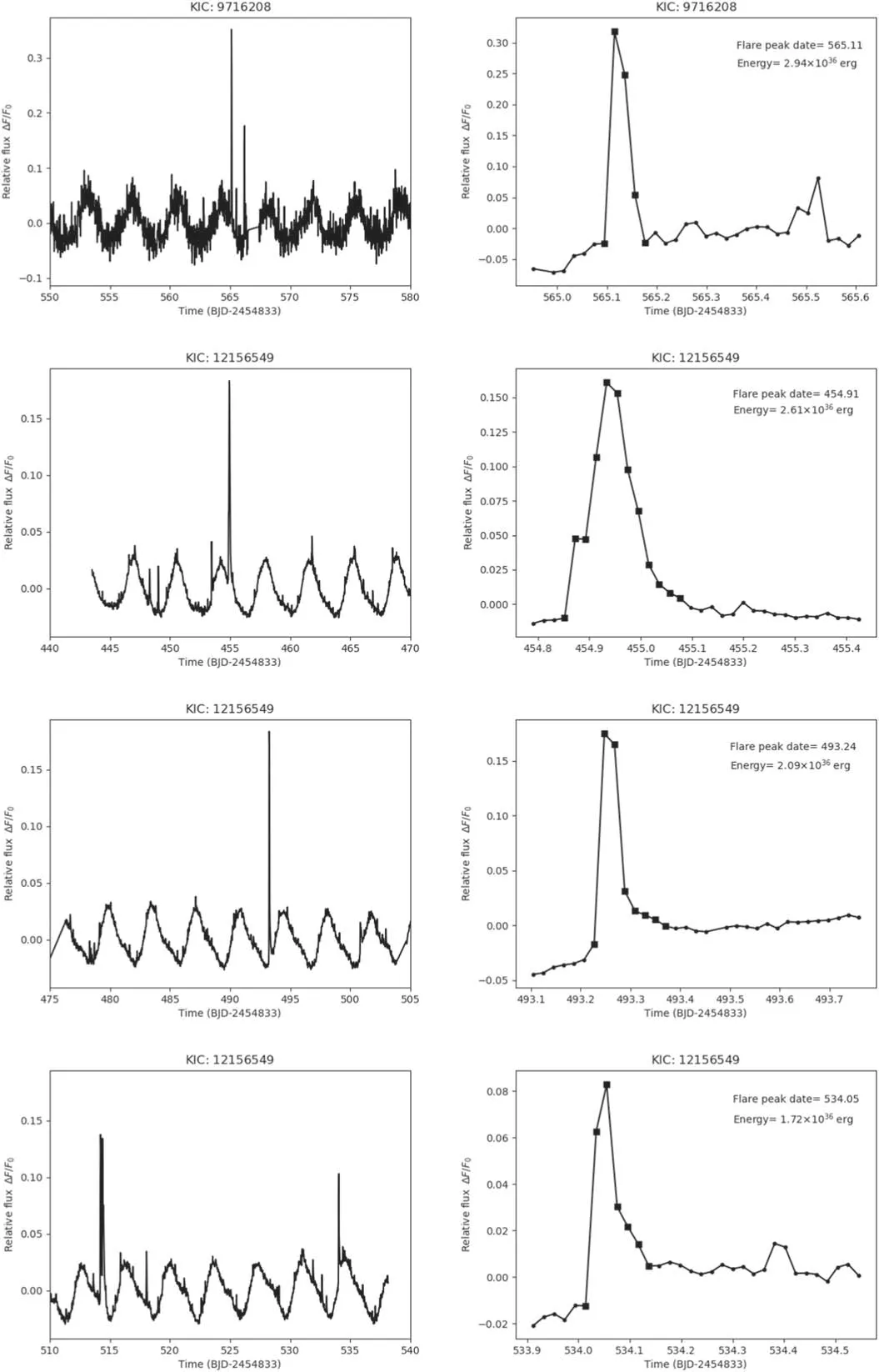
Figure 5.Four of the most energetic super-flares detected during Q0 to Q6.The left panels depict the light curves of these super-flares over a period of 30 days.The super-flares that occurred on these light curves are enlarged in the right panels.The super-flare energy and peak date are displayed in the upper right corner.The black squares in the right panel correspond to the data points for the super-flares from beginning to end.

In Figure 6 are six log-log scale histograms demonstrating the frequency distribution of super-flares in Q0 to Q6.We estimated the error bar for each bin using the equation

Figure 6.Log-log scale histograms showing the frequency distribution of super-flares on G-type dwarfs (5100 K ≤Teff<6000 K and glog 4.0>) in Q0-Q6.The error bar for each bin was calculated by taking the square root of the sum of the squared weights in that bin.(a)Distribution of the number of observed super-flares per recorded flare peak amplitude.(b)Distribution of flare frequency as a function of flare energy.The distributions of all stars and slowly rotating stars are represented by solid and dashed lines,respectively.All G-type dwarfs and slowly rotating G-type dwarfs have power-law indices of 2.2 and 2.0,respectively.(c)Distribution of flare frequency as a function of flare energy of all cool stars (5100 K ≤Teff<5600 K,gray-dashed histogram),and all hot stars (5600 K ≤Teff<6000 K,white-solid histogram).(d)The same as(c),but for flares on slowly rotating stars with Prot>10 days.The average energy of the two red bins was used to calculate the occurrence frequency of super-flares with energy of 2.11×1035 erg.(e)and(f)are the comparisons between the findings of this study and those of Shibayama et al.(2013)on all G-type dwarfs and Sun-like stars,respectively.

wherewrepresents the individual weights of the events that belong in that bin.As a result,when the number of the event in the bin is insufficient,the error bars in statistics are large(Shibayama et al.2013).

Figure 6(a) represents the distribution of the number of observed super-flares per observed flare peak amplitude.The number of observed super-flares is 1298,and the measured amplitude range is approximately between 8×10−4and 3×10−1.Figure 6(b,c and d) displays the super-flare frequency distributions as a function of the flare energy.However,each histogram has a different collection of superflare stars according to the purpose of the comparison.Thexaxis indicates the energy of super-flares in erg,and they-axis represents the number of super-flares per star per year per unit energy.Figure 6(b) features a comparison between frequency distributions of super-flares on all G-type dwarfs (white-solid histogram) and slowly rotating G-type dwarfs withProt>10 days (gray-dashed histogram).The number of detected superflares is 1298 for all G-type dwarfs and 229 for slowly rotating G-type dwarfs.Since they-axis is the number of super-flares per star per year per unit energy,we determine the weight for each bin using

whereNosis the number of observed stars,see Table 3,Dis the duration of the observation period in seconds andEis the super-flare energy that belongs to that bin.Due to the lack of rotation period data,Table 3 was produced based on an estimate using table 6 from Shibayama et al.(2013),where we calculated the ratio of the number of cool,slowly rotating stars and hot,slowly rotating stars to the number of observed stars in Shibayama et al.(2013),and similarly for the fast-rotating stars.We then applied,i.e.,extrapolated,these ratios to our data to estimate the number of fast and slowly rotating stars relative to their effective temperature.When comparing the distribution of super-flares on all G-type dwarfs and super-flares on slowly rotating G-type dwarfs,we can confirm that the occurrence frequency of super-flares on all G-type dwarfs is higher than the occurrence frequency of super-flares on slowly rotating G-type dwarfs.Furthermore,it is evident from the two fitted straight lines,(solid line) for all G-type dwarfs and (dashed line) for all slowly rotating G-type dwarfs,that the frequency distributions of super-flares on all G-type dwarfs and slowly rotating G-type dwarfs follow a power-law relation given by

Table 3The Number of Observed G-type Stars Nos Distributed According to their Effective Temperature Teff and Rotational Period Prot

where the index α ≃2.2±0.1 for all G-type dwarfs and α ≃2.0±0.3 for all slowly rotating G-type dwarfs.We note that this result is similar to that of Shibayama et al.(2013).Figure 6(c) presents the distribution of super-flares as a function of energy on all cool G-type dwarfs with 5100 K ≤Teff<5600 K (gray-dashed histogram) with 255 observed super-flares,and all hot G-type dwarfs with 5600 K ≤Teff<6000 K (white-solid histogram) with 1043 observed super-flares.Figure 6(d) is the same as 6(c) but for slowly rotating G-type dwarfs with rotation period more than 10 days.The number of observed super-flares for cool slowly rotating G-type dwarfs is 78,and 151 for hot slowly rotating G-type dwarfs (Sun-like stars).From the two figures,we find that the frequency of super-flares is higher in cool G-type dwarfs than in hot G-type dwarfs,again confirming the previous results of Maehara et al.(2012);Shibayama et al.(2013).Note that the difference in the occurrence rate of super-flares between the cool and hot stars in this study is not as large as in Maehara et al.(2012);Shibayama et al.(2013).We can explain this by noting that our sample’s number of cool stars constitutes approximately 15.1%of the total number of the sample while hot stars make up 84.9% of the total number of the sample,see Table 3.In contrast,in Shibayama et al.(2013),cool stars make up about 48.7% of the total number of the sample,and hot stars constitute 51.3% of the total number of the sample.In addition,if we compare the number of superstars relative to the observed stars,we find that this rate is higher in cool stars than in hot ones,see columns 5,8 and 13 in Table 4.

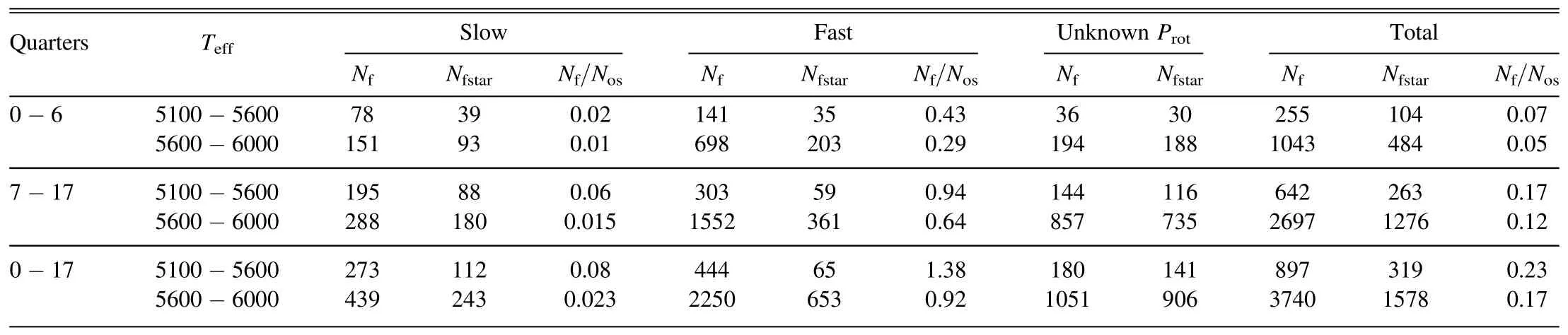
Table 4The Number of Super-flares and Super-flare Stars on G-type Dwarfs

We calculated the occurrence frequency rate of super-flares from the number of observed super-flaresNf,the number of observed starsNosand the observation durationD(Maehara et al.2012;Shibayama et al.2013).The super-flare energy distribution in Q0-Q6,which ranges from 2.84×1033erg to 2.94×1036erg,varies from Q7-Q17 and Q0-Q17,which ranges from 2×1033erg to 1.42×1038erg,resulting in a different energy bin distribution.Therefore,in order for the energy used to derive the occurrence frequency rate of superflares to be close for each section of the analysis(Q0-Q6,Q7-Q17 and Q0-Q17),we used the average energy of the two red bins in 6(d),which equals 2.11×1035erg and is close to the energy 2.26×1035erg that was used in Q7-Q17 and Q0-Q17,red bins in Figures 7(d)and 8(d)respectively.As a result,the rate of super-flare incidence with energy of 2.11×1035erg is 2.46×10−4flares per year per star,corresponding to a superflare occurring on a star once every 4070 yr.This result is within about 80% of the occurrence rate of super-flares with energy of 1035erg found by Shibayama et al.(2013),which equals one super-flare in 5000 yr for each star.Figure 6(e)and 6(f) provides a comparison between the results of this study(solid-white-histogram)and the Shibayama et al.(2013)study(gray-dashed-histogram).Figure 6(e) depicts the frequency distribution of super-flare energy for all G-type dwarfs,∝α−,where α ∼2.2 in each of the two studies.Figure 6(f) shows the same comparison but for Sun-like stars with 151 super-flares in this study and 44 super-flares in Shibayama et al.(2013).Note from the two comparisons that the estimated energy of super-flares in this study is higher than that of Shibayama et al.(2013).Our justification for this is related to the differences in the Kepler Data Releases between DR9 and DR25 used in Shibayama et al.(2013) and this study,respectively.Since the Kepler pipeline was updated between DR9 and DR25,PDCSAP light curves for each target may also be updated.Also,the previous work may have used slightly different parameters since the effective temperature and radius of some Kepler targets have been updated since then,resulting in different Kepler IDs for each spectral type.Another factor that may affect the energy value is that in this study,we used the flux difference rather than the flux to determine the start time of the flare.This can result in an extra data point between the flare’s start and end times,resulting in higher energy.To find how our method affects the energy calculation results,we run the script on 279 flare stars from Shibayama et al.(2013)in order to compare the energy results derived from the script with those in Shibayama et al.(2013).We found 503 common super-flares with the same start-time of the flare between Shibayama et al.(2013) and our script result.Then we calculated the correlation coefficient between the energy values and we observed an energy increase for our study,with a correlation coefficient of 0.66 between the two energies.Such small correlation coefficient points to a sizeable difference in the flare energy estimates between this study and Shibayama et al.(2013),for the reasons listed above.

4.1.2.Super-Flares on G-type Dwarfs in Q7-Q17

We detected 3339 super-flares on 1539 G-type dwarfs during the course of 930 days of continuous monitoring;483 superflares on 268 slowly rotating stars are among them.In the case of Sun-like stars,we found 288 super-flares on 180 of them.According to our findings,318 G-type dwarfs out of 1539 exhibit several super-flares whereas 1221 show only one superflare.A total of 38 out of 180 Sun-like stars have several superflares,and 142 Sun-like stars have just one super-flare.The most powerful super-flare discovered during this period had an energy of 1.42×1038erg,an amplitude of 22.75 and a duration of 0.06 days.Figure 7 depicts four log-log scale histograms displaying the frequency distribution of super-flares in Q7 to Q17,similar to Figure 6,but without the comparisons in 6(e)and 6(f).The distribution of the number of observed superflares per observed flare peak amplitude is shown in Figure 7(a).The total number of super-flares detected is 3339,with amplitudes ranging from 7.5×10−4to 35.Figure 7(b,c and d)has a similar format as Figure 6(b,c and d).A comparison of super-flare frequency distributions on all G-type dwarfs(whitesolid histogram) and slowly rotating G-type dwarfs (graydashed histogram) is shown in Figure 7(b).The power-law index for super-flare frequency distributions on all G-type dwarfs α ≃2.2±0.1 and for slowly rotating G-type dwarfs α ≃2.1±0.4.Figure 7(c)and 7(d)displays the distribution of super-flares as a function of flare’s energy according to the effective temperature of the star for all G-type dwarfs and slowly rotating G-type dwarfs respectively,where the number of detected super-flares is 642 on all cool G-type dwarfs(graydashed histogram) and 2697 super-flares on all hot G-type dwarfs (white-solid histogram) in 7(c) and 195 super-flares on cool slowly rotating G-type dwarfs (gray-dashed histogram)and 288 super-flares on hot slowly rotating G-type dwarfs(white-solid histogram)in 7(d).The red bin in 7(d)affirms that the occurrence frequency rate of super-flares with energy of 2.26×1035erg is 1.31×10−4flares per year per star,corresponding to a super-flare occurring on a star once every 7640 yr.We note that this value is somewhat larger than similar results for Q0-Q6 and Q0-Q17.

Figure 7.The same as in Figure 6(a)–(d)but for Q7-Q17 data.The FFDs in(b)for all G-type dwarfs and slowly rotating G-type dwarfs have power-law indices of 2.2 and 2.1,respectively.The red bin in (d) was used to calculate the occurrence frequency of super-flares with energy of 2.26×1035 erg.

4.1.3.Super-Flares on G-type Dwarfs in Q0-Q17

Combining the two previous observations,we find that during 1424 days of continuous monitoring,we found 4637 super-flares on 1896 G-type dwarfs.Among them are 712 super-flares on 355 slowly rotating stars.We discovered 439 super-flares on 243 of the Sun-like stars.Our findings suggest that 397 stars out of 1896 G-type dwarfs experience more than one super-flare,whereas 1499 stars undergo only one superflare.A total of 55 out of 243 Sun-like stars have several superflares,whereas 188 Sun-like stars have just one super-flare.Table 5 lists some super-flare stars with their parameters and the number of super-flare occurrencesNf.The entire results can be found at https://github.com/akthukair/AFD.Figure 8,similar to Figure 7,displays four log-log scale histograms of the frequency distribution of super-flares as a function of flare energy in Q0 to Q17.Figure 8(a)features the distribution of the number of observed super-flares per observed flare peak amplitude.The amplitude of the 4637 detected super-flares ranges between 7.5×10−4and 35.6.Figure 8(b,c,and d)’s format is similar to that of Figure 7(b,c and d).Figure 8(b)compares the frequency distributions of super-flares on all G-type dwarfs (white-solid histogram) and slowly rotating G-type dwarfs (gray-dashed histogram).Super-flare frequency distributions on all G-type dwarfs have a power-law index of α ≃2.0±0.1,while slowly rotating G-type dwarfs have a power-law index of α ≃2.2±0.3.A comparison of the distribution of super-flares as a function of flare energy for all G-type dwarfs and slowly rotating G-type dwarfs,according to the effective temperature of the star,is provided in Figure 8(c) and (d).In Figure 8(c),there are 897 super-flares on all cool G-type dwarfs (gray-dashed histogram) and 3740 superflares on all hot G-type dwarfs (white-solid histogram),273 super-flares on cool slowly rotating G-type dwarfs (graydashed histogram) and 439 super-flares on hot slowly rotating G-type dwarfs (white solid histogram) (d).The occurrence frequency rate of super-flares with energy equal to 2.26×1035erg is 2.29×10−4flares per year per star,corresponding to a super-flare occurring on a star once every 4360 yr,as shown in the red bin in Figure 8(d).

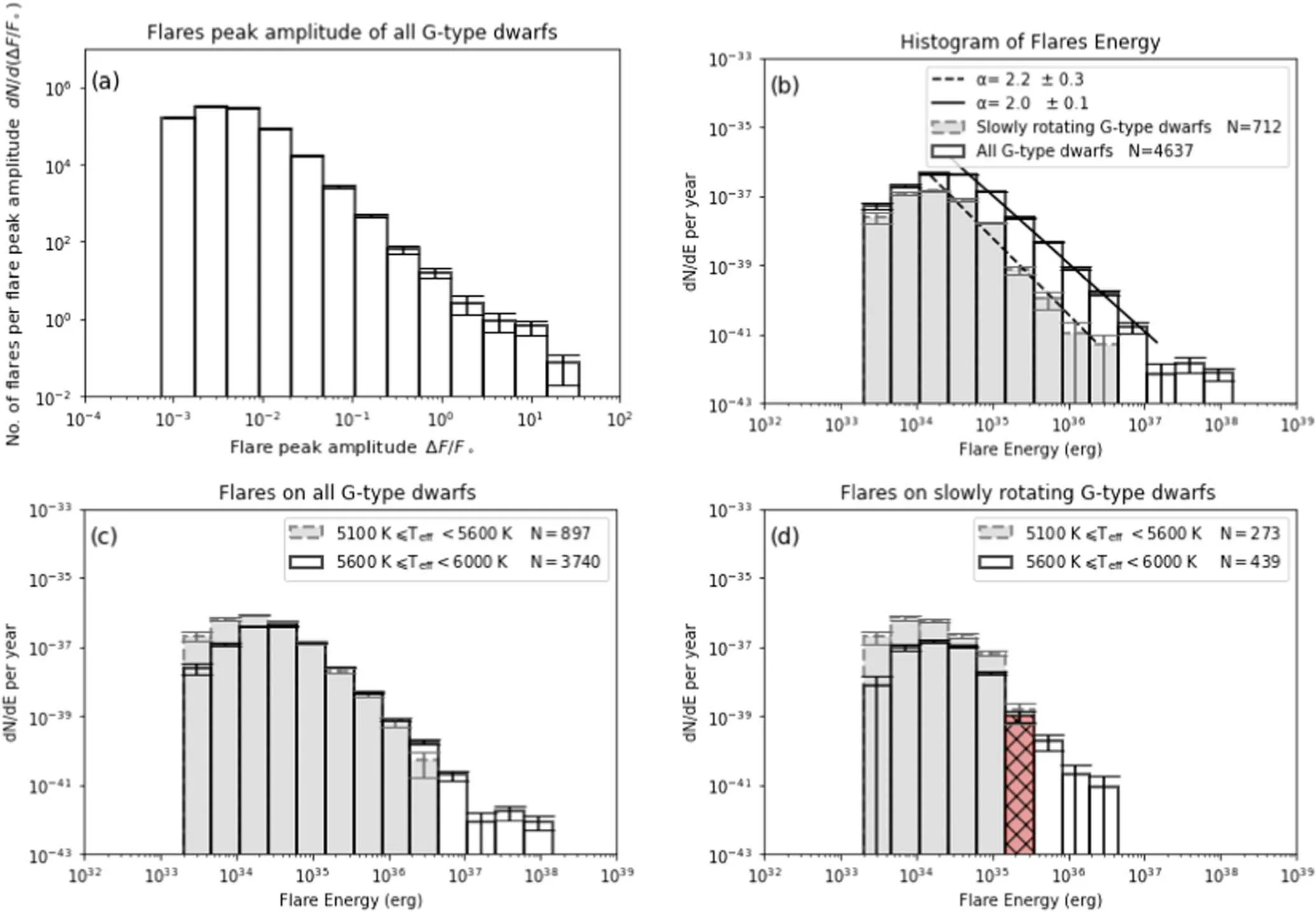
Figure 8.The same as in Figure 6(a)–(d)and 7 but for Q0-Q17 data.The FFDs in(b)for all G-type dwarfs and slowly rotating G-type dwarfs have power-law indices of 2.0 and 2.2,respectively.The red bin in (d) was used to calculate the occurrence frequency of super-flares with energy of 2.26×1035 erg.

Table 5The Parameters of Super-flare Stars (G-type) with the Number of Flares Nf

4.1.4.Comparison with Okamoto et al.(2021)

In Section 4.1.1,we compared our results with those of Shibayama et al.(2013) since that section only discusses the statistical analysis of super-flares in (Q0-Q6) as in the Shibayama et al.(2013) study.Here we compare our findings to those of Okamoto et al.(2021),who used the complete Kepler primary mission data set and the Gaia DR2 catalog to conduct the most recent statistical analyses of super-flares on solar-type (G-type main sequence) stars.

1.The sample size used to search for super-flare differs between the two studies.Okamoto et al.(2021) limit the study to 11,601 stars whose brightness variation amplitude and rotation period values were reported by McQuillan et al.(2014).In this study,our sample size is more than two times larger than that of Okamoto et al.(2021) (25442 G-type main sequence stars).

2.We both followed the same method applied in previous studies (Maehara et al.2012,2015;Shibayama et al.2013) to detect super-flares,except that Okamoto et al.(2021) improved the technique by developing an improved version of the flare-detection method,in which a high-pass filter was used to remove rotational variations caused by starspots.Furthermore,the sample biases on the frequency of super-flares were examined,taking both gyrochronology and completeness of the flare detection into account.Our method does not include these improvements.

3.We found 4637 super-flares on 1896 G-type dwarfs.The number of super-flares and super-flare stars is ∼2 and ∼7 times larger than the 2341 super-flares and 265 superflare stars in Okamoto et al.(2021),respectively.In addition,we found 439 super-flares on 243 Sun-like stars based on the Shibayama et al.(2013) definition for Sunlike stars (5600 K ≤Teff<6000 K,glog 4.0>andProt>10 days).If we consider the rotation period range in Okamoto et al.(2021)for Sun-like stars(Prot=20–40 days),the number of flares would be reduced to 51 superflares on 38 Sun-like stars.This is approximately twice the number of super-flares and Sun-like stars that were discovered in Okamoto et al.(2021),with 26 super-flares on 15 Sun-like stars.

4.Our result includes 183 flare events on 41 G-type dwarfs,similar to those observed by Okamoto et al.(2021).Table 6 presents a comparison of these events between the two studies,showing the parameters for each Kepler ID,the flare peak date and its energy.This result constitutes 3.95%and 7.82%of the total flares detected in our work and Okamoto et al.(2021),respectively.This low percentage in similar events is due to the different Kepler IDs in the samples used in the two studies.The effective temperature and stellar radius values in Okamoto et al.(2021) were taken from Gaia DR2 in Berger et al.(2018),resulting in different Kepler IDs for G-type main sequence stars.We observed an increase in the flare energy estimate of our study compared to that in Okamoto et al.(2021),with a correlation coefficient of 0.91 between the two energies.

Table 6Comparison between the Common Flare Events Detected in this Work and Those Observed by Okamoto et al.(2021)

5.We calculated the α index for the FFDs as a function of the flare energy (∝E−α) for different ranges ofProt(<5 days,5–10 days,10–20 days and 20–40 days)in two effective temperature ranges (5100–5600 K and 5600–6000 K) as shown in Figure 9 and compared our results with those of Okamoto et al.(2021) as displayed in Table 7.The results are very similar,with α indexes around-2,confirming Okamoto et al.(2021)’s previous finding,which also aligns with earlier research on superflares on solar-type stars (Shibata et al.2013;Shibayama et al.2013;Maehara et al.2015).From this similarity,we believe that the effects applied in Okamoto et al.(2021)by applying a high-pass filter and examining the sample biases on super-flare occurrence rates considering gyrochronology and the completeness of flare detection have no significant affect on our final results.

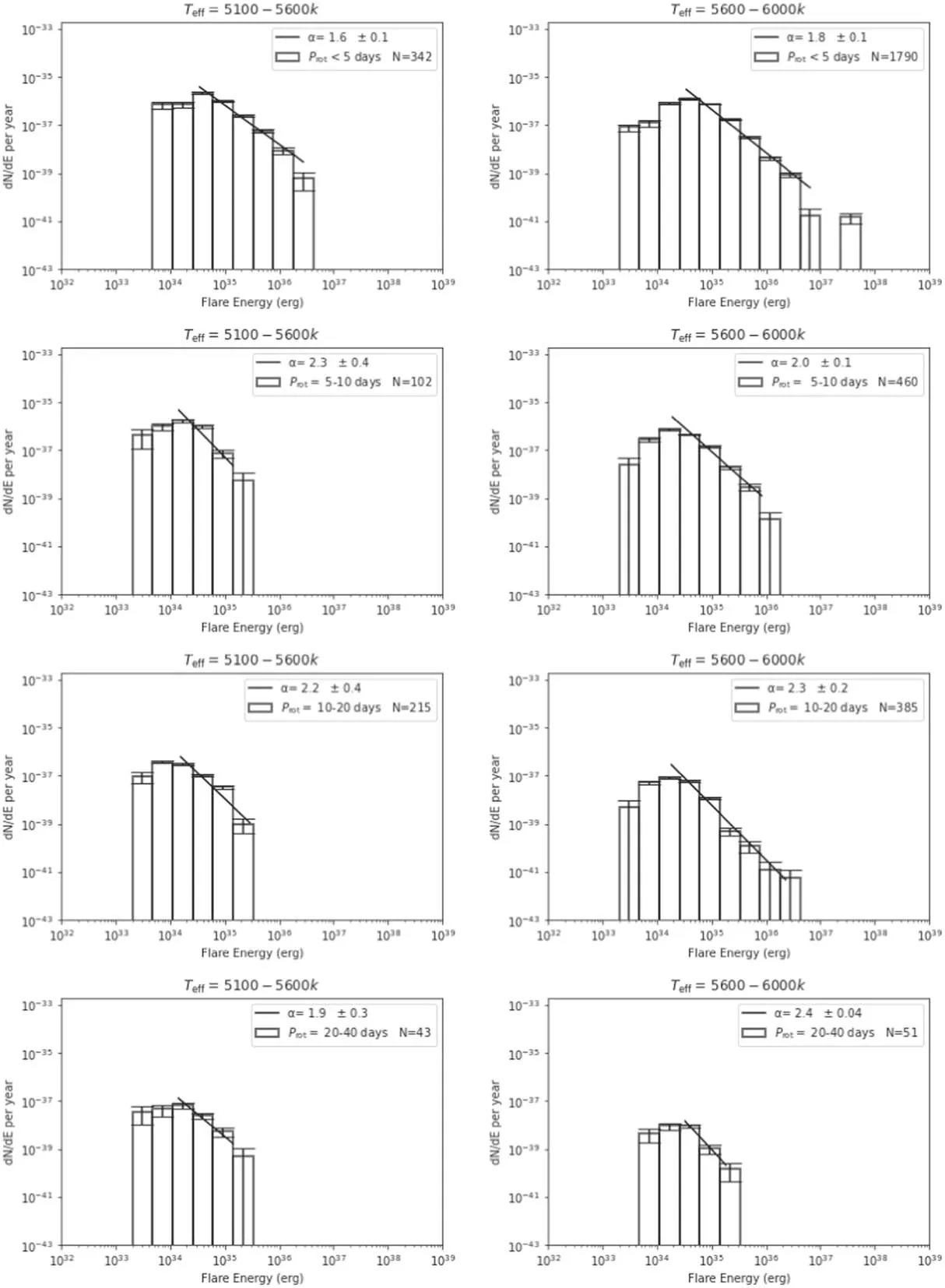
Figure 9.The FFDs as a function of the flare energy(dNdE ∝ E−α)for different ranges of rotation periods(Prot:<5 days,5–10 days,10–20 days and 20–40 days)divided by the effective temperature Teff=5100–5600 K on the left panel and Teff=5600–6000 K on the right panel.α is the power-law index,and N is number of super-flares for each Prot.

Table 7Comparison of the α Index for the Flare Frequency Distributions as a Function of the Flare Energy (dNdE ∝ E−α) for Each Prot Range

Table 7Comparison of the α Index for the Flare Frequency Distributions as a Function of the Flare Energy (dNdE ∝ E−α) for Each Prot Range

6.We used a different stellar parameter catalog(q1_q17_dr25_ stellar catalog) however,we obtained similar results.Different stellar properties in the Gaia catalog,especially for radius,did not significantly affect our results,as shown in Table 6,as the correlation coefficient between energies in the two data sets ≃0.91.

4.2.Super-Flares on Other Spectral Type Stars

We detected a total of 11438 super-flares on 1740 stars of other spectral types during 1424 days of continuous observation of dwarfs of 2653 A-type,10898 F-type,10307 K-type and 2222 M-type.The entire results can be found at https://github.com/akthukair/AFD.

For A-type dwarfs,we found 321 super-flares on 136 stars;44 of these stars show more than one super-flare and 92 stars exhibit only one super-flare.The duration of these super-flares can be up to 0.27 days,and their flare maximum amplitude is 0.47.The largest flare energy we have determined is 8.91×1037erg,with an amplitude of 0.28,and it lasted for 0.16 days.

As for F-type dwarfs,we discovered 1125 super-flares on 522 stars;106 of these stars exhibit several super-flares,whereas 416 stars manifest only one.These super-flare durations can be up to 0.57 days,and their flare amplitude can reach 0.08.Our calculations show that the highest flare energy we have found was 2.35×1036erg,which had an amplitude of 0.036 and lasted for 0.2 days.

Moving on to K-type dwarfs,we detected 4538 super-flares on 770 stars;304 show several super-flares,while 466 stars exhibit just one.The duration of these super-flares can be up to 0.3 days,and their amplitude can reach 1.04.The largest flare energy we measured is 2.82×1036erg,with an amplitude of 0.057 and a duration of 0.28 days.

For M-type dwarfs,we found 5445 super-flares on 312 stars;256 of which have several super-flares and 56 have only one.These super-flare durations can be up to 0.82 days,and their flare amplitude varies between 0.002 to 15.1.The highest flare energy we recorded was 1.59×1035erg,and it has an amplitude of 15.1 and a duration of 0.18 days.

Figure 10 shows the FFD on different spectral types,which follows a power-law relation (∝E−α).We used roughly the same energy range to obtain the best fit for α index in order to compare between the results.In order to maintain accurate statistics,we disregarded bins at the end of the histogram that contain a small number of flares (five or less).

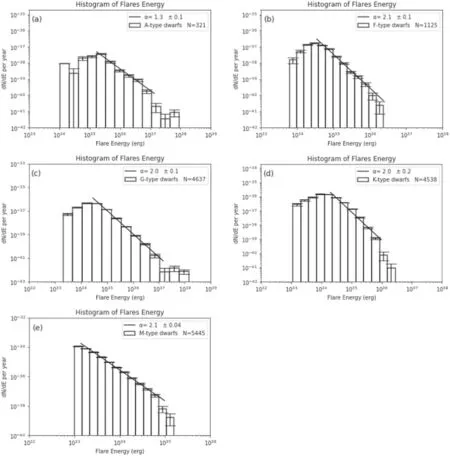
Figure 10.Log-log scale histograms showing the frequency distribution of super-falres organized by the stellar spectral type,with the α index of the power-law relation(dNdE ∝ E−α)and the number of super-flares for each spectral type indicated.We used approximately the same energy range for the fitting in all panels and ignored the bins toward the end of the histogram with a limited number of flares.

Yang&Liu(2019b)reported a total of 162,262 flare events on 3420 flaring stars.They found that the FFDs from F-type stars to M-type stars have an index α ∼2,while α ∼1 for the FFD of A-type stars.In our study,we found that the α index is about 2 for spectral types from F-type to M-type stars.In particular α ≃2.1±0.1 for F-type stars,α ≃2.0±0.1 for G-type stars,α ≃2.0±0.2 for K-type stars and α ≃2.1±0.04 for M-type stars.These results are consistent with the previous results of Yang&Liu(2019b).Shibata et al.(2013)found that for Sun-like stars,the FFD of nanoflares,microflares,solar flares and super-flares follows a power-law relation with α ≃1.8.It means that the underlying mechanism which is generating these flares by magnetic reconnection occurs in similar physical conditions (Yang &Liu 2019b;Cliver et al.2022).It is thought that the same fundamental process that causes solar flares also causes flares in late-type stars(F-M).A convective envelope is necessary for the dynamo that generates the magnetic fields in these stars.For magnetic fields to become strong enough to rise and emerge into the stellar atmosphere,which results in the generation of flares,this convective envelope must be sufficiently deep (Pedersen et al.2017).The similarity of α index indicates that the process of producing flares in various spectral types from F-type to M-type stars is similar and is based on magnetic reconnection (Yang &Liu 2019b).

However,the situation is different for A-type stars,as the α index for the FFD differs from the rest and is α ≃1.3±0.1.It is widely expected that these stars cannot have flares.For stars to produce flares,they must have a deep outer convection zone,powerful large-scale magnetic fields or powerful winds produced by the radiation.Normal A-type stars are devoid of these characteristics.Hence they should not flare (Pedersen et al.2017).Moreover,according to stellar evolution theories,A-type stars are unlikely to flare because of their weak magnetic fields,and their thin or nonexistent surface convection zone,prevent a magnetic dynamo from operating (Van Doorsselaere et al.2017).However,through a visual inspection of the light curves,Balona (2012,2013) found flare events in the light curves of 33 A-type stars.To study the origin of these flares,Pedersen et al.(2017) reported a new,detailed analysis of these 33 A-type stars and verified the existence of flares in 27 of them.Balona(2015)observed 1833 and 424 A-type stars in LC and SC,respectively,during Q0-Q12 using visual inspection.In the LC and SC,51 and 10 A-type stars,respectively,manifest evidence of flare activity.Moreover,24 new A-type stars with flaring activity have been discovered by Van Doorsselaere et al.(2017).

Table 8 shows the number of super-flares for each spectral type,whereNf(candidates)is the number of flare candidates captured by the code when the flux difference exceeded the threshold limit,Nf(conditions)is the number of flares that met all the conditions,Nf(check)is the number of flares we verified using visual inspection of the light curves andNf(exclude)is the number of flares that we excluded due to their irregular,chaotic shape after the visual inspection of the light curves.By analyzing this table,we notice a large fraction of excluded flares are in the A-type stars compared to the M-type stars.This can be explained by the different flare conditions in the stars.One difference can be that the sizes of A-type starspots are much larger than those of M-type,with different magnetic reconnection conditions,resulting in flares with irregular,chaotic shapes of the light curves in A-type stars.This is possibly why A-type stars have a different α index.Table 9 shows the incidence of flares for each stellar spectral type.Since our study considers only main sequence stars,the number of stars is limited to a specific radius range for each spectral type,and therefore the number of stars in this study is much smaller than in other studies such as Yang&Liu(2019b).Thus the flare incidence appears in larger numbers than in those studies.The flare incidence gradually increases from F-type to M-type stars from 4.79%to 14.04%because of the increase in the convection zone depth (Yang &Liu 2019b).However,the incidence of flares in A-type stars,5.13%,is higher than that in F-type stars,4.79%,which contradicts the theoretical expectation.From an A-type star to an F-type star,the star’s outer layer changes from a radiative envelope to a convective envelope,allowing F-type stars to operate a solar-like dynamo.In contrast,A-type stars struggle to create and maintain a magnetic field (Yang &Liu 2019b).These results are also consistent with Balona(2015);Van Doorsselaere et al.(2017);Yang &Liu (2019b),who analyzed stars of any size,not just those on the main sequence discussed here.The deviation of the α index in A-type stars from the other stellar types,the rise of flare incidence rate compared to F-type stars and the high percentage of excluded flares compared to the rest of the spectral types are all indications that A-type stars may generate flares in a different,peculiar manner.

Table 8The Ratio Rate of Excluded Flares for Each Spectral Type

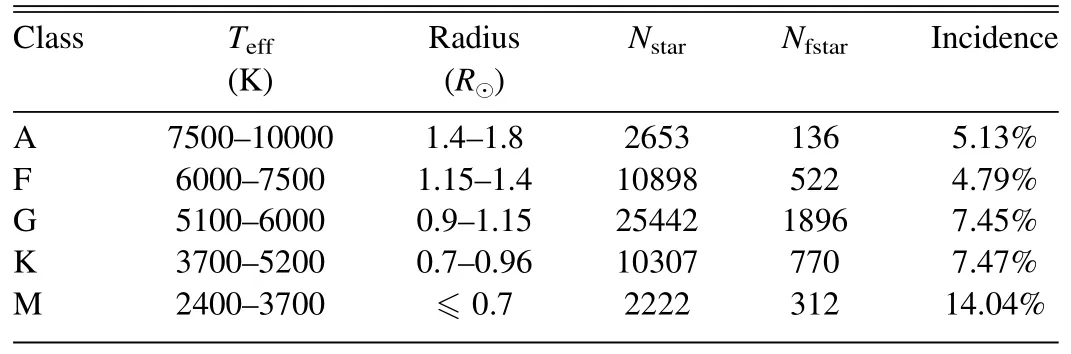
Table 9The Number of Stars Nstar,Flare Stars Nfstar and Flare Incidence for Each Spectral Type

5.Conclusion

Using a bespoke Python script written by us,we performed an automated search for super-flares on main sequence stars of types A,F,G,K and M in all of Kepler’s long-cadence data of DR25 from Q0 to Q17,following the Maehara et al.(2012);Shibayama et al.(2013) technique.We used the Harvard spectral classification to determine each target’s spectral type based on its effective temperature and radius.For A,F,G,K and M type stars,we studied a total of 2653,10898,25442,10307,and 2222 main sequence stars,respectively.As a result,we detected 4637 super-flares on 1896 G-type dwarfs during 1424 days of continuous observation by Kepler.Using these new data,we studied and compared the statistical properties of the occurrence frequency rate of super-flares using three distinct data sets,namely,Q0-Q6,Q6-Q17 and Q0-Q17.According to our estimates for the Q0-Q17 data set,a superflare on G-type dwarfs with an energy of 1035erg occurs on a star once every 4360 yr.By comparing three data sets (0-6,7-17 and 0-17),the statistics of flares look very similar,which is indicative of the fact that the flare occurrence statistic does not change on the timescale of 17 quarters.In addition,we compared our results with those of Okamoto et al.(2021)regarding the FFD and the α index for the power-law relation.The similarity of the results supports the consistency with Okamoto et al.(2021)’s prior research.This suggests that the high-pass filter and analysis of sample biases on super-flare occurrence rates that Okamoto et al.(2021) performed while considering gyrochronology and the completeness of the flare detection had no appreciable impact on our final results,which is one of the motivations for our study.Also,we compared 183 similar flare events to Okamoto et al.(2021)on a case-by-case basis,as in Table 7.We noted an overestimation of the flare energy for our study compared to Okamoto et al.(2021).Despite using a different catalog of stellar parameters,available to us,we found that the results are consistent with Okamoto et al.(2021).The different stellar parameters in the Gaia catalog had no significant effect on our findings as illustrated in Table 6.Moreover,we detected a total of 321,1125,4538 and 5445 super-flares on dwarfs of 136,522,770 and 312 A,F,K and M type stars respectively,during 1424 days of continuous observation.We determined the distributions of super-flare occurrence rates as a function of super-flare energy.We found that for all spectral types of stars,from F-type to M-type,the FFD as a function of flare energy follows a power-law relation with∝E−αwhere α ≃2.0 to 2.1.This demonstrates that the power-law index α is similar to those of solar flares(∼2) (Shibayama et al.2013).The power-law index values’similarity suggests that similar physical conditions produce the flares,by the mechanism which is thought to be magnetic reconnection.In contrast,the obtained value of α index 1.3 of the FFD for A-type stars indicates that their flare conditions are distinct from those of the other stellar types.We observed a general rise in the flare incidence rate from 4.79% to 14.04%for F-type to M-type stars respectively.However,the flare incidence rate is higher in A-type stars,5.13%,than in F-type stars,4.79%,contrary to the theoretical expectation (Yang &Liu 2019b).These results are similar to those found by Balona(2015),Van Doorsselaere et al.(2017),Yang &Liu (2019b).

In general,flares with smaller amplitude tend to be more challenging to detect.Therefore,the detection completeness of flares with smaller amplitude is lower than that of larger ones,and the actual frequency of flares with smaller amplitude would be higher than the observed one.In addition,as discussed in Okamoto et al.(2021),the flare-detection threshold proposed by Maehara et al.(2012);Shibayama et al.(2013) depends on the rotation period and the amplitude of rotational modulations.In relation to the evaluation and discussion on the flaredetection completeness,which has a significant impact on the power-law slope of the FFD,we would like to remark that since the power-law slope for G type-stars is similar to that of Shibayama et al.(2013) and for A-type stars that of Yang &Liu (2019b),we believe that a lack of dedicated analysis of flare-detection completeness has no significant impact on our results.

In relation to the contamination of flares on close neighboring stars we would like to remark that since the spatial resolution of the Kepler space telescope is not high(∼4〞pixel−1),some stars have close neighbors within the photometric aperture.As pointed out by Maehara et al.(2012);Pedersen et al.(2017),flares on close neighboring stars can produce false flare signals in the target light curve.These false flares may potentially have an impact on the flare frequency.Although we excluded the stars having neighboring stars within 12〞,we believe that this is sufficient despite the fact that not all faint stars are cataloged.Again our belief is backed up by the fact that the power-law slope for G type-stars is similar to that of Shibayama et al.(2013) and for A-type stars that of Yang &Liu (2019b).

In relation to how we determine the flare energy range used for fitting the observed FFD to the power-law function,we would like to acknowledge the fact that the number of flares in the lower energy bins would be much smaller than the actual flare frequency.Therefore,one should choose the energy range in which the detection completeness issue can be negligible.In our case,the choice of which leftmost energy range bins to ignore was done intuitively by eye,similar to Yang &Liu(2019b).

Acknowledgments

Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST).STScI is operated by the Association of Universities for Research in Astronomy,Inc.,under NASA contract NAS5-26555.Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX13AC07G and by other grants and contracts.

The authors would like to thank Deborah Kenny of STScI for kind assistance in obtaining the data,and Cozmin Timis and Alex Owen of Queen Mary University of London for the assistance in data handling at the Astronomy Unit.

A.K.Althukair wishes to thank Princess Nourah Bint Abdulrahman University,Riyadh,Saudi Arabia and Royal Embassy of Saudi Arabia Cultural Bureau in London,UK for the financial support of her PhD scholarship,held at Queen Mary University of London.

Data Availability

All data used in this study were generated by our bespoke Python script that can be found at https://github.com/akthukair/AFD under the filename AFD.py and other files in the same GitHub repository.The data underlying this article were accessed from Mikulski Archive for Space Telescopes(MAST,https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html).The long-cadence Kepler light curves analyzed in this paper can be accessed via MAST STScI (2016),https://doi.org/10.17909/t9488n.The Kepler stellar parameters table for all targets can be found at Kepler (2019).The derived data generated in this research will be shared on reasonable request to the corresponding author.

ORCID iDs