A Data-driven Method for Realistic Covariance Prediction of Space Object with Sparse Tracking Data

Hong-Kang Liu ,Bin Li,2 ,Yan Zhang ,and Ji-Zhang Sang,2

1 School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;bli@sgg.whu.edu.cn

2 Hubei Luojia Laboratory,Wuhan 430079,China

3 Xi’an Satellite Control Center,Xi’an 710043,China

Abstract Covariance of the orbital state of a resident space object (RSO) is a necessary requirement for various space situational awareness tasks,like the space collision warning.It describes an accuracy envelope of the RSO's location.However,in current space surveillance,the tracking data of an individual RSO is often found insufficiently accurate and sparsely distributed,making the predicted covariance (PC) derived from the tracking data and classical orbit dynamic system usually unrealistic in describing the error characterization of orbit predictions.Given the fact that the tracking data of an RSO from a single station or a fixed network share a similar temporal and spatial distribution,the evolution of PC could share a hidden relationship with that data distribution.This study proposes a novel method to generate accurate PC by combining the classical covariance propagation method and the data-driven approach.Two popular machine learning algorithms are applied to model the inconsistency between the orbit prediction error and the PC from historical observations,and then this inconsistency model is used for the future PC.Experimental results with the Swarm constellation satellites demonstrate that the trained Random Forest models can capture more than 95%of the underlying inconsistency in a tracking scenario of sparse observations.More importantly,the trained models show great generalization capability in correcting the PC of future epochs and other RSOs with similar orbit characteristics and observation conditions.Besides,a deep analysis of generalization performance is carried out to describe the temporal and spatial similarities of two data sets,in which the Jaccard similarity is used.It demonstrates that the higher the Jaccard similarity is,the better the generalization performance will be,which may be used as a guide to whether to apply the trained models of a satellite to other satellites.Further,the generalization performance is also evaluated by the classical Cramer von Misses test,which also shows that trained models have encouraging generalization performance.

Key words: celestial mechanics–methods:analytical–miscellaneous

1.Introduction

Space Situational Awareness(SSA)encompasses intelligence and surveillance of all space objects,prediction of space events,possible collisions,threats,and activities (Bobrinsky &Del 2010).SSA-related tasks include collision probability computation (Xu &Xiong 2014),sensor tasking and scheduling (Jiang et al.2017),uncorrelated track (UCT) association (Liu et al.2021),catalog maintenance,and anomaly detection,etc.Common among these applications is that a proper uncertainty characterization of the orbit state of an individual resident space object(RSO),mainly referring to the orbital covariance(Poore et al.2016),is required.Unrealistic covariance could lead to failure in predicting collisions,false correlation between UTCs and RSOs,inefficient use of sensor resources,and undetected maneuvers.The notion of covariance realism is not without precedent,but a clear definition has been often out of reach(Vallado&Seago 2009).In other tracking domains,the term of covariance consistency is used in place of the term covariance realism (Drummond et al.2007),which describes the proper characterization of the covariance of the state of a system.Covariance realism requires the estimate of the mean to be the true mean(namely,the estimate is unbiased)and the covariance to possess the right size,shape,and orientation (namely,consistency).Most often,covariance realism is synonymous with the covariance accuracy,gauged by comparing the predicted covariance (PC) with the truth orbit prediction error(PE)(Vallado&Seago 2009).

In the orbit dynamics field,an estimate of the orbit state and its covariance matrix is obtained from an orbit determination(OD) process with available measurements,and then the state and covariance are propagated forward,namely orbit prediction(OP),in which the PC describes a certain accuracy envelope of the predicted orbit state.In this process,the orbital dynamics is usually assumed to be deterministic,and the measurement errors are of Gaussian distribution and regarded as the only uncertainty source.Thus,the estimated covariance matrix only accounts for the measurement noises,known as the noise-only covariance(Montenbruck&Gill 2000),also called formal state covariance(Lopez et al.2021).In this way,other sources of uncertainty,such as force model errors,are typically not accounted for during the OD and subsequent OP.This usually leads to an overly-optimistic or conservative covariance matrix,eventually,causing the accuracy loss of covariance realism.

Techniques of achieving better covariance realism continue to be increasingly needed by the Space Surveillance and Tracking(SST) and Space Traffic Management (STM) operators(Montenbruck&Gill 2000).A number of statistical techniques have been developed by researchers with various degrees of success to produce relatively realistic covariance.The mechanisms used by space communities differ in their realizations,and can be sorted into two main types:(1)scaling methods,which inflate the covariance by certain factors with the purpose of increasing the volume of a Gaussian ellipsoid based on statistical metrics;some researchers propose to compute such scale by increasing the initial position uncertainty to match the velocity error,whereas another option is to employ the Mahalanobis distance of the orbital differences to find the scale factor;(2)State Noise Compensation(SNC)method,which uses a process noise matrix to consider the uncertainties in the dynamics system or measurements.A well-known example is the realistic covariance predictions of the Earth Science Constellation satellites: Aqua,Aura,and Terra (Junkins et al.1996;Duncan &Long 2006;Pawloski et al.2018).It is necessary to clarify that the Consider Analysis method is another example of the SNC technique which accounts for modeling uncertainties in the covariance estimation and prediction.Besides,there exist other techniques conceived to improve covariance realism instead of modeling the sources of uncertainty.For instance,state and covariance representation in mean orbital elements(Junkins et al.1996)and in the nonlinear reference frames (Aristoff et al.2021) are widely studied to prolong the realism maintenance upon propagation.These methods have been widely used and achieved great improvements in covariance realism.However,they have limitations of various degrees from a practical point of view.The scaling method lacks physical insight and only relies on a statistical analysis of empirical data to provide covariance corrections.It is difficult to be generalized or extrapolated since the scaling factors are not linked to any physical process.The SNC method requires a significant amount of tuning,and this tuning is prone to failure.Moreover,the type of dynamics in the SNC method appears limited by the pre-assumed Gauss-Markov functional form.Appending dynamics parameters to the state can be an effective method for recovering dynamics,but it requires a known noise pattern for those unmodeled dynamics.

With the employment of more accurate sensors and the growing population of RSOs (Zhang et al.2022),the potential number of newly discovered objects is likely to increase by an order of magnitude within the next decade,thereby placing an ever-increasing burden on current operational systems.The above limitations have made existing techniques ill-suited for future needs.Moving forward,the implementation of new,innovative,robust,and intelligent methods for covariance realism is required to enable the development and maintenance of the present and future space catalog and to support the overall SSA mission.

Machine learning (ML) techniques have been developed significantly in recent years and promise viable approaches within the space domain's solution space to augment,supplement,and potentially replace traditional methods with encouraging performance.Different algorithms and tools have been developed and utilized in the SSA domain.Liu and Schreiber reported the application of a deep neural network for an automatic classification scheme for space objects based on a single track of a photometric light curve(Liu&Schreiber 2021).Mereta et al.showed that in the case of multi-revolution transfers between near-earth objects(NEOs)the ML approach is vastly superior to the commonly used impulsive Lambert estimate (Mereta et al.2017).Shen et al.developed both manifold and deep learning methods to determine the space object behavior pattern classification (Shen et al.2019).Curzi et al.proposed a novel approach to estimate TLE prediction errors using recurrent neural network (Curzi et al.2022).Moreover,using ML modeling techniques to reduce OP errors shows promising results.Peng and Bai studied the support vector machine,Gaussian Processes,and artificial neural network to improve the OP accuracy (Peng&Bai 2018,2019,2021).Li et al.achieved better than 70% OP accuracy improvement by applying the ML-predicted OP errors to correct the physics-based OPs,and the 7 days OP errors were reduced from hundreds or even thousands of meters to only tens of meters through the error correction obtained from the learned error models (Li et al.2020,2021).These applications clearly show the excellent capability of ML in SSA,which prompts authors to apply ML methods to achieve better covariance realism.

In order to achieve better covariance realism,various approaches have been attempted,including new propagation methods,reference frames representing covariance,and calibration methods.In this paper,we aim to improve the realism of the propagated covariance by the calibration approach,a novel method is proposed to produce more realistic covariance through the combination of the classical error propagation model and the data-driven model.The evolution pattern of the inconsistency between the error of the propagated orbit (PE) and the PC is learned by the ML method from historical data and is then used to produce realistic covariance for future epochs via the error compensation.A complete ML framework for the improved covariance realism is implemented in three steps,including constructing the data set of the inconsistency between PC and measured PE,training error models with ML methods,and correcting the future PC using ML-predicted inconsistency.In the developed ML framework,the trained inconsistency model can be used as a corrector to the physics-based orbit error prorogation system.Thus,accurate covariance can be obtained over a long duration if the trained ML model captures the majority of the inconsistency.

In what follows,the generation of state and its associated initial covariance,as well as their predictions,are described in Section 2.The implementation of the ML method to improve the covariance is given in Section 3.In Section 4,experiments with sparse satellite laser ranging (SLR) data of the low-Earth-orbit (LEO) Swarm satellites are conducted to show the performance of the proposed method.In the final section,some conclusions are drawn.

2.Statistical Characterization of Orbit Prediction Errors

In the real orbital data process,the initial orbit covariance(IOC) is generated as a part of an OD solution and then propagated forward with the linear or nonlinear models.Ideally,the PC provides appropriate information of the PE over the prediction time span.In this section,the fundamental computations of the PC and PE are presented.

2.1.PC Generation

An accurate orbit state is determined from an orbit estimation process,and the batch least-square (BLS) is typically used to provide a best-fit orbit matching the available observations(Montenbruck &Gill 2000).IOC is also obtained in the BLS OD system,providing a measure of the variability and correlation of the estimated orbit state parameters.A mathematical description of the IOC matrix can be found in Ref.(Vallado &Seago 2009).The IOC at the initial epocht0,denoted as P(t0),is expressed as

where A is the partial-derivative matrix (partial derivatives of the measurements with respect to the estimated parameters);W is the weight matrix of the measurements,andis the posterior unit variance.

However,Equation(1)disregards the inherent uncertainty of dynamic and measurement models.In this sense,P(t0) is commonly found to underestimate the true characterization of the estimated orbit state uncertainty.Evidence of this phenomenon is abundant in literature (Junkins et al.1996;Duncan &Long 2006;Lopez et al.2021).For the sake of simplicity and efficiency,linear dynamics and linear propagation of covariance are assumed.Linear covariance propagation is an analytical method that is relatively straightforward,in which the IOC is propagated fromt0to the future epochtusing the state transition matrix φ(t,t0) as follows

where P(t)is the propagated covariance matrix att.

The diagonal elements of P(t) yield the variances of the position and velocity components while the off-diagonal terms are a measure of the correlation between errors of individual components.The final size of P(t0) is a 6×6 matrix,which means that the uncertainties in the dynamical parameters such as drag or solar radiation pressure coefficients are not included,such that the unmodelled dynamical parameter uncertainty will contribute to the inconsistency of the PC.To better understand the error characteristics,the covariance in the Cartesian coordinate system is usually transformed into the RSW coordinate system,whereR,S,andWrepresent the radial,intrack (in-plane normal to radial),and cross-track directions,respectively (Vallado 2007).In the following,σPis used to denote the square root of the variance of a position or velocity component in the RSW coordinate system.Considering that a principal application of the covariance is in the conjunction assessment (CA) of space objects,where only the position portion of the covariance is used,it is reasonable to focus only on the position portion of the covariance.So,in our study,only the position covariance,denoted as,is concerned,and the velocity covariance will not be discussed in the following.

2.2.PE Generation

PE,the difference between the OPs and their “truth” or precise ephemerides,is a measure to assess the accuracy of state predictions.The position differences are calculated and then expressed in the RSW coordinate frame for the orbit error analysis.The root mean square (RMS) value of PEs for each position component is computed in a preset interval (e.g.,an orbital period),and used as a measure of the PE magnitude,representing the 1σ error.This process is basically the same as that in Ref.(Duncan &Long 2006).In the following,the computed positional sigma errors,denoted as,are regarded as the realistic magnitude of the state uncertainty in the OD and OP process.

In theory,if the PC is accurate,it should be consistent with the computed σC,that is,the magnitudes of σCand σPshould be close to each other to some extent.Figure 1 shows an example of inconsistency between σCand σP.So,the problem turns out to bridge the gap between σPand σC.Hence,the inconsistency or the gap is computed as

Figure 1.Schematic illustration of the inconsistency between PC and PE.

Because σCis computed from the differences between the propagated orbit and the“truth”orbit,it is regarded as reliable.In this sense,the inconsistency is mostly due to σP.The key idea of this study is to model the inconsistency and then apply the modeled inconsistency pattern to correct PC,such that the inconsistency between the corrected σPand σCis significantly reduced.

3.Development of ML Framework

In our previous studies (Li et al.2020,2021),an ML framework to improve OP accuracy has been developed.This study expands the ML framework to include the capability of modeling the inconsistency,defined in Equation (3).The modified ML framework is illustrated in Figure 2.

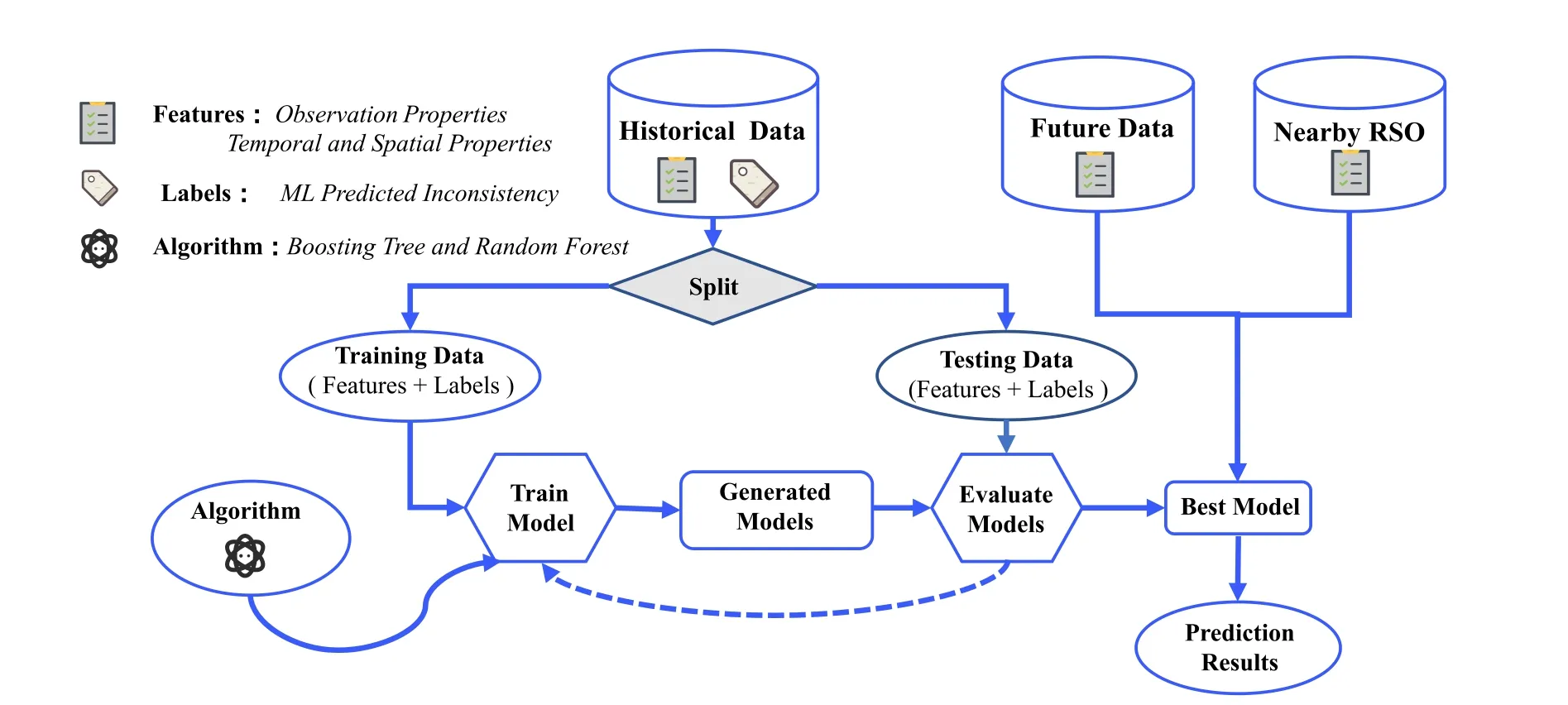
Figure 2.ML framework for improved covariance realism.

3.1.Data Source

Given that optical and radar measurement data is difficult to obtain,and emulated measurements may not fully simulate real observation scenes,so,in this study,we consider the singlestation SLR tracking scenario.The tracking station is Changchun SLR station (CHAL),China,with its geodetic latitude of 43°79,the longitude of 125°44,and altitude of 274.90 m.In the single-station SLR tracking scenario,the collected consolidated ranging data(CRD)tracklets are sparse,mostly less than three passes daily for an SLR satellite.The CRD is available at the International Laser Ranging Service(ILRS) data center (ftp://cddis.gsfc.nasa.gov/).Also,the precise Consolidated Prediction Format (CPF) orbits of the SLR satellites are downloaded and used as the reference to compute the PE.

Training data samples are generated based on a consistency analysis of orbital differences between the reference orbits and predicted orbits,which are from independent ODs using the SLR data.The graphical representation of the orbital differences is depicted in Figure 3.Furthermore,the orbital differences are time-tagged,forming the population of the PEs and associated PCs with respect to the prediction time length.

Figure 3.OD sliding windows for generating PE and PC.

Sufficient statistical samples for the ML would be acquired by considering a sufficient number of independent orbits.To compute the orbital differences between the reference and predicted orbits,two additional steps are performed:

1.Requirement on the number of data points per track,for a track to be used in the OD,it must have at least three data points.

2.Requirement on the number of tracks within 3 days,for an OD process to be successfully completed,there are at least 2 tracks available over 3 days (the OD span used in this study).

The sliding-window manner favored by NASA (Pawloski et al.2018;Duncan &Long 2006) has been implemented and is also demonstrated effective in the work (Li et al.2020;Lopez et al.2021).In this study,the sliding step is set as 1 day.

For clarity,we briefly introduce the OD strategy and settings used in this study.The equations of motion of an Earth-orbiting satellite in the Earth-centered inertial(ECI)coordinate system is given by a system of three second-order differential equations of

In our experiments,the main perturbations considered are listed in Table 1.An orbit determination and analysis software for processing the ranging observations is developed by Li et al.(Li et al.2020).It applies the Cowell integrator to propagate satellite position and velocity vectors in Equation (4),and the BLS algorithm for the optimal estimations.In the BLS OD process,three days’laser tracking arcs of a satellite are used to compute the optimal estimation of the state.Commonly,model parameters,such asCdandCr,may be estimated.However,given the sparsity of tracking arcs,only the position and velocity of the satellite are estimated.The OD fit span is set starting at the epoch time of the first tracking arc.The initial orbit state is computed from the latest TLE before the OD fit span.Further details about the orbit estimation strategy can also be found in Ref.(Li et al.2020).

Table 1OD Setting in Force Modeling

3.2.Learning Features

ML method works on sample data(training and testing data)to learn the hidden pattern.For a given problem,the success of the learning relies strongly on data preparation.Generally,the sample data consists of the input Z,usually a vector,and the outputY.The objective of the learning is to capture the mappingY=f(Z).Therefore,it is imperative that the sample data should be well-prepared.Determining the target variableYis always straightforward.In this study,the target variableYis the inconsistency defined in Equation(3).But the choice of feature variables is subjective,as there are many latent features affectingY.Fortunately,most ML algorithms are not sensitive to irrelevant feature variables.Theoretically,the more feature variables are included in Z,the more accurate but complex the trained model would be.Therefore,it is usually favorable to take into account the main feature variables that affectYin ML learning.

The target variableYrefers to the inconsistency as:

Based on the above configuration of (Z,Y),there exists an implicit mathematical relation that maps Z toY.With the wellprepared samples generated in a sliding-window manner and the well-designed feature variables,the mapping function,defined asY=(Z),is hopefully found through the ML training,if this mapping exists.Then,the trained ML model is expected to find the relationship between the PC and PE.In particular,if data beyond the learning period,or at a future epoch,are input into the trained model,the model is expected to make good predictions about the relationship between the PC and PE at the epoch.The correction to PC can be performed as below.

where σMLis the modified sigma that will replace the original σPin applications.

The residual error Δe corresponding to σMLis

It is expected that Δe,the inconsistency between σCand σML,should be significantly less than σgapif the ML models capture the underlying pattern.

The performance of the learned ML model can now be assessed using the following metric

4.Experimental Results

The developed ML framework is applied to train the orbit covariance inconsistency models of three Swarm satellites.To implement the ML framework,the boosting tree (BT) and random forest(RF)(Friedman et al.2000)are employed.These two models are both based on the decision tree,have high accuracy with moderate computation complexity,are versatile in case of large data sets having high dimensionality,and have a high degree of interpretability (Molnar 2020).Sharing well reputation in the ML community,these two models of different mechanisms are chosen to validate each other and to demonstrate the effectiveness of the ML framework.More details about BT and RF models are referred to in Ref.(Russell&Norvig 2003).In the experiments,the propagated orbits and PC are obtained from the OD/OP system first.Then,the CPF orbits are used as references to compute the PE.Lastly,the PC is calibrated by the learned ML model such that the inconsistency between the correctedis reduced.

To demonstrate the learning and generalization capabilities of the ML models,the three satellites in the Swarm constellation are chosen as the test objects.The three identical satellites,named Alpha,Bravo,and Charlie (or A,B,and C),were launched into three near-polar orbits on 2013 November 22.Swarm A and Swarm C form the lower pair of satellites flying side-by-side (1°.4 separation in longitude at the equator) at an altitude of 460 km and at the inclination of 87°.4,whereas Swarm B is cruising at a higher orbit of 520 km and at 88°inclination angle.Orbit parameters of the Swarm satellites are summarized in Table 2.

Table 2Orbit Parameters of Swarm Satellites

4.1.Statistical Characterization of Tracking Data in OD

The pattern of the inconsistency between the PC and PE is to be learned from historical data.The SLR tracking data of the Swarm satellites at CHAL in 2021 January have the distribution properties shown in Figure 4.The left of Figure 4 represents the distribution of the data points of each arc,and the right represents the distribution of the pass durations.The bottom of each box is the first quartile,the top of the box is the third quartile,and the line inside of the box is the median.

Figure 4.SLR data distributions of Swarm satellites in January 2021 at CHAL station.

From Figure 4,it can be found that Swarm A and Swarm C have similar distributions of data points and track durations owing to their pair-flying attribute,while Swarm B has the best distributions among the three satellites.There are 35,27,and 26 tracks in 2021 January for Swarm A,Swarm B,and Swarm C,respectively.The average track duration of each satellite is 88.4 s,157.7 s,and 83.7 s,with their corresponding average number of data points per track being 17,29,and 16.

With the available data gathered by the CHAL station within 90 days from January to April in 2021,the BLS OD with a 3 days fit span is carried out,and the OD span is sliding forward with a 1 day step.35/56/43 OD runs are successful for Swarm A,Swarm B,and Swarm C,respectively,and each of these successful OD runs produces the initial orbit state and IOC,which are then propagated forward for 7 days from the end of the OD span,generating the required PC and PE.Here,the 7 days OP is believed sufficient for a timely and reliable SSA application.

4.2.Inconsistency between PC and PE

Examination of the statistical characterization of PC and PE reveals that PC is a very poor representation of PE dispersion.Figure 5 displays an example growing trend of the position components of PC and PE of Swarm A over a 7 days OP time span.It is noted that each PC/PE point is computed once for 1.5 hr.

Figure 5.PC compared with PE in the RSW coordinate system,Swarm A.

Figure 5 clearly shows the inconsistency between the PC(blue dots) and the PE (red dots) when only sparse data is available.That is,(,,)greatly underestimate(,,) during the OP time span.(,) are virtually not growing.While the in-track position erroris significantly larger than the other two components with its magnitude reaching nearly 40 km at the end of 7 days,similar results can be noticed in Duncan &Long (2006).Because the in-track position error contributes the most to the position error,great attention is paid to the model training of inconsistency in the in-track position component.It is observed that at the end of the 7 days propagation,the ratio of PC to PE in the in-track direction is about 0.015,the magnitude of this kind of ratio is also found in references(Zaidi&Hejduk 2016),and the level of PC is within the range of what is considered normal for this type of analysis.

It is very intuitive to see that the gaps between(,,)and(,,)increase as the prediction time increases.It is also clear that PC does not provide the proper characterization of the true orbit prediction errors.In fact,they are too conservative or“optimistic”to describe the errors of the predicted orbits.

Figure 6 shows the inconsistency values in the S direction over 7 days OP span of Swarm A from the whole data set in 3 months.Examination of Figure 5 has shown that the in-track position gap is significantly larger than the other two components.In this figure,different growth trends can be observed,and this can be explained by the fact that the dynamic model errors and observation conditions produce different OP accuracy.So,technically speaking,the more diverse observation properties contain,the more inconsistency patterns can be displayed.

Figure 6.The inconsistency over the 7 days OP span,Swarm A.

4.3.ML Model on the Training and Testing Data

The 3 months time span is divided into a 1 month training period and a 2 months validation period.That is,the data in January are used to train the models.To avoid overfitting,the Cross-Validation (CV) that splits the data set in the training period into training and testing data is applied.Randomly chosen 70%of the whole data set is used to train the model for each of the R/S/W directions while the remaining 30%is used to evaluate the performance of the learned models.As discussed earlier,the feature variables of the testing data are the input to the model,and the output is the ML-predicted covariance inconsistency in each direction.

Figure 7 presents the results of the trained BT (left) and RF(right) models on Swarm A training data (3137 samples).The horizontal axis represents the prediction duration.In the figure,the green dots are the“true”inconsistency σgap_trueand the red dots are the ML-predicted inconsistency σgap_pred.It is intuitive to see the RF models perform better.It can be seen that the red dots with the BT model,on the left of the figure,are more dispersed,while the red dots with the RF model,on the right of the figure,are much closer to the “true” green dots,or even overlapped.The performance metricPMLof the BT model is 35.7%,34.9%,and 20.1% for the radial,in-track,and crosstrack inconsistency,respectively.Great improvement can be noticed when the RF model is used,with thePMLbeing 1.2%,1.5%,and 0.4% for the radial,in-track,and cross-track inconsistency,respectively,indicating that the trained models have captured about 99% of the underlying pattern.Therefore,the conclusion can be made that the trained models capture the inconsistency in the training data set very well.Similar results are obtained for Swarm B and Swarm C.

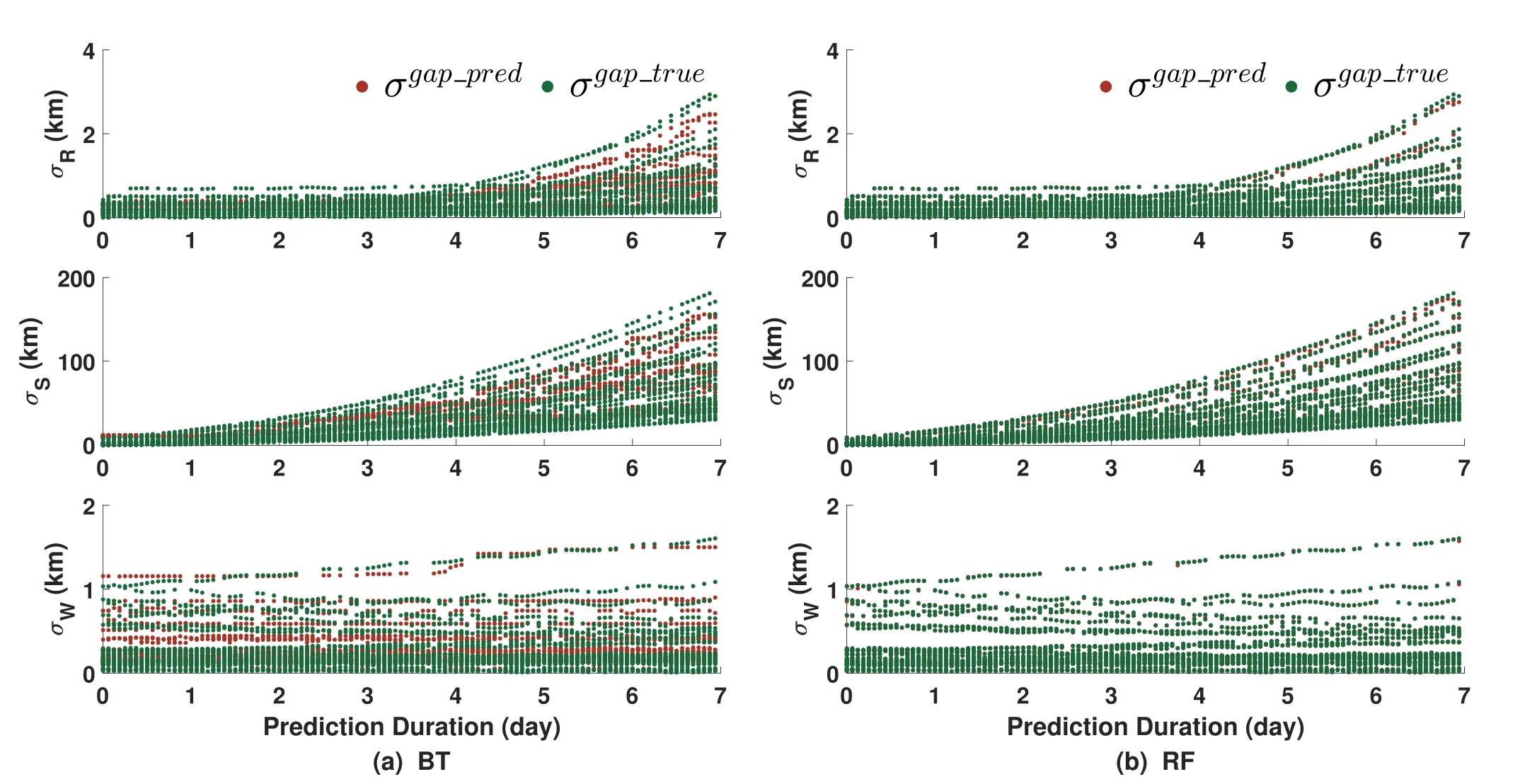
Figure 7.Results of the trained BT(a)and RF(b)models on the training data(3,137 samples),Swarm A.

Figure 8 shows the results of the performance of the trained BT(left)and RF(right)models on the testing data(1344 samples)for Swarm A.These two models show a slight drop when they are used on the testing data.Meanwhile,the RF model outperforms the BT model.It is intuitive to explain that if the trained model performs poorly on the training data,it is difficult to obtain satisfactory predictions on the testing data.

Figure 8.Results of the trained BT(a)and RF(b)models on the testing data(1,344 samples),Swarm A.

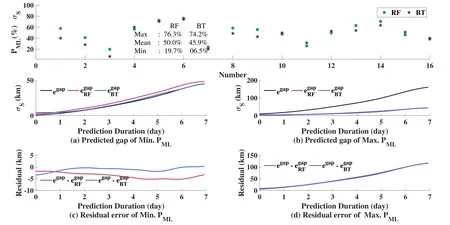
Figure 9.Improved covariance realism beyond the training period,Swarm A.

Figure 10.Improved covariance realism beyond the training period,Swarm B.

Figure 11.Improved covariance realism beyond the training period,Swarm C.

Table 3 gives thePMLvalues of the trained models on the training data and testing data for all Swarm satellites.

Table 3Performance PML of the BT and RF Models in Fitting the Training and Testing Data

In Table 3,it can be seen that allPMLvalues are below 50%for both the BT and RF models,indicating more than half of the inconsistency errors can be corrected by the trained models.Moreover,the trained RF models are much more powerful than the trained BT models in capturing the inconsistency patterns on the same training and testing data,with thePMLall less than 5%in all three directions for all the satellites.Overall,the developed ML framework is capable of capturing the majority of the underlying inconsistency pattern with well-designed samples.If the learned patterns agree well with the realistic patterns,the trained models can be employed to predict the inconsistency in future epochs.

4.4.Generalization of ML Model to Future Epochs

For practical applications,one is more concerned with the performance of the trained ML models on new data in the future.So,a desirable ML model should have good generalization capability,that is,making good predictions with new input beyond the training period.In this study,after the trained models on the inconsistency are obtained from the use of the historical covariance inconsistency data set,it can be generalized to future epochs to predict new inconsistency at these epochs.Thus,the improved covariances are obtained via the model compensation.

In order to demonstrate the generalization capability of the trained ML models on the data beyond the training period,the data in 2021 January are used to train the ML models,and the data in February and March are used as the validation data for the evaluation of capability in the generalization into future of the trained ML models.The performance metricPMLof the ML models on the validation data is shown in Figures 9–11.Since the in-track error contributes the most to the position error,in this section,only the in-track component is displayed.In each of these figures,the improvement in terms of the percentage of every single validation case is presented.Besides,panels(a)and(b) in each figure show the predicted gap when the model performs best(lowest inPMLmetric value)and performs worst(highest inPMLmetric value),with panels(c)and(d)showing the residual errors after the corrections are made to PC.

Observing Figures 9–11,there are 16/30/28 validation cases for Swarm A,Swarm B,and Swarm C,respectively.It reveals that the RF and BT models behave similarly and both show good generalization ability.The means ofPMLof the trained BT and RF models on the validation data are all below 50%.The trained models perform best on the swarm B data set,with the meanPMLmetrics of RF and BT models at 25.4% and 26.7%,respectively.This means that the ML-predicted inconsistency over the 7 days OP time span is significantly reduced compared with the original one,confirming the models capability of the generalization into the 2 months after the training time.The trained models of Swarm A are poorer in generalization ability,with the meanPMLvalues at nearly 50%,while the trained models of Swarm C perform moderately.It is also seen that thePMLon the validation data is generally larger than that on the training data.This is owing to the variations of the orbital environment which cause the inconsistency pattern in the validation time to deviate from the pattern in the training time.In each of these figures,the best-performed predictions and the worst-performed predictions have also been shown in panels(a)and (b),respectively,with the corresponding residual errors shown in(c)and(d).

4.5.Generalization of ML Model to Other Satellites

In this section,the generalization capability of trained models of a satellite into other satellites is examined,which is highly important for the SSA applications,since there may be no sufficient samples for training a desirable model of other RSOs.So,the question is whether the learned models of a specific RSO can be applied to other RSOs that result in improved covariance realism.

Here,the trained models of Swarm A are applied to Swarm B and Swarm C.The Swarm A models are trained using all data over the 3 months.The validation data is also over the same 3 months.The performance of Swarm A model's generalization to Swarm B is summarized in Figure 12.It is observed that the mean metricPMLexceeds 100%,reaching 282.1%and 400%for the RF and BT models,respectively,which indicates the trained models have very poor capability of generalization to Swarm B.As can be seen in Figure 12(a) and (b),the predicted gap,given by the RF and BT models,are about 40 km at the end of the 7 days OP span,while the true inconsistencyegapis about 10 km.An obvious reason is that the two satellites are at different altitudes,one at 460 km and the other at 520 km.This causes the data conditions and orbital environment,especially the atmospheric drag conditions,for the two satellites significantly different,and thus the inconsistency patterns of Swarm B would be significantly different from those of Swarm A.As a result,the trained models of Swarm A unlikely to contain all the patterns of Swarm B,and this causes large fluctuations of the predicted inconsistency when the Swarm A models are applied to Swarm B.This phenomenon would be further analyzed from the perspective of data similarity in Section 4.6.

Figure 12.Performance of Swarm A models generalization to Swarm B.

On the other hand,the generalization performance of Swarm A models to Swarm C,shown in Figure 13,is much better.The meanPMLvalues are 21.1%and 36.7%for RF and BT models,respectively,and the performance of the RF model is better than that of the BT model.It is also noted that the curves of the predicted gaps are smooth.As can be seen from subplot(a),the best performance of the RF model,with thePMLequal to 4.2%,is achieved,which means more than 95% of the gap can be corrected by the trained RF model.Even in the worst validation case,as shown in(b),the predicted gap is larger than the true gap but the difference between them appears acceptable.For example,the propagated PC and RF-model predicted gap at the end of the 7 days OP span are 4.31 km and 33.46 km,respectively,while the PE is 33.76 km,making the difference reduced from 29.44 to 4.01 km.The rewarding performance of the trained Swarm A model's generalization to Swarm C is promising.This can be attributed to the fact that the two satellites are pair-flying such that they share similar data conditions and orbital environments.

4.6.Generalization Capability Analysis

The generalization of Swarm A models to Swarm B and Swarm C exhibits vastly different performances.An analysis is necessary to understand the possible causes.

Generally speaking,the generalization performance of the trained models is strongly dependent on the similarities between the training data and application(validation)data.That is,when the training data and application data have high similarities,good generalization performance can be expected.In real scenarios,this assumption may not be satisfied,rendering the generalization performance difficult to be guaranteed.In this section,we propose the use of Jaccard similarity to measure the similarity between training and validation data sets and to examine the relation between the data similarity and generalization performance.

Jaccard similarity is a common proximity measurement that can be used to find the similarity between two data sets(Baroni&Buser 1976).Given two data sets,PandQ,their intersection isP∩Qwith the size |P∪Q| (the number of members in the intersection set),and the union isP∪Qwith the size |P∪Q|.Then,the Jaccard similarity between them is defined as

The Jaccard similarity will be 0 if the two sets do not have any member in the intersection set and 1 if the two sets are identical.It is intuitive to see thatJgets higher when the two data sets are more alike.Additionally,this function can be used to find the dissimilarity between two sets by calculating 1 −J.This metric is applicable to a wide range of applications due to its generality.

We now use the Jaccard similarity to measure the similarity between the training and validation data sets.To apply Equation (9),the training data set is defined asP,and the validation data set asQ,both of which are formed in the following way.Recalling that the training data set or the validation data set span over the same 3 months,and each data set has different numbers of OD runs.Each 3 days OD span is divided into several equal intervals.For every interval,the availability of the SLR track is examined.If there is a track in an interval,the track is coded as 1,otherwise as 0.For example,in the interval from 1.6 to 3.2 hr(assuming the interval length is 1.6 hr),there is a track of Swarm A,then the track is coded as 1.For a 3 days OD span,the data set is encoded as[1,0,1,...,0],where the number of encoded values is the number of intervals.In this way,the training or validation data set is constructed,as shown in Figure 14,where each row represents one 3 days OD span.Here,the 3 days OD span is divided into nine intervals of a length of 8 hr,actually,this figure can be regarded as the temporal distribution of the observation attributes.

Figure 14.Illustration of the encoded data set.

The similarity between the training and validation data sets is examined in terms of temporal and spatial closeness.Consider the case that,there is a track from the training data set,and in the same interval,there is a track from the validation data set.The starting time of a track is denoted asttfor the track from the training data set ortvfor the track from the validation data set.The azimuth and elevation at the point of maximum elevation of a track are denoted as(az,el)tor(az,el)v,which are converted to the unit vector rtor rv.The introduction of temporal and spatial closeness is to assist us in determining whether a model from data sets of one object(say Object A)can be generalized to an OD case of another object (say Object B).To do this,we first find the maximum J from all J values each is computed using Equation (9) with one data set of Object A and the data set of Object B.(For example,Object A has 30 data sets,we will have 30 J values.)Then,if the maximum J is larger than the threshold of J (Jthreshold),we proceed to compute the angle between the data set of Object B and the data set of Object A which has the maximum J using Equation(10).Last,if the angle is larger than its threshold α,we decide that the model of Object A can be generalized to the data set of Object B.

For other cases where there is no or only one track from either the training or validation data set in an interval,the intersection in the interval is not available.The intersection set of the training and validation sets can now be formed,and the number of intersected tracks is counted.Figure 15 gives the schematic illustration of the spatial distribution of data.

Figure 15.Schematic illustration of the spatial distribution of data set.

When constructing the union set,only the interval having at least one track from either the training or validation data set is regarded as a member of the union,and thus the number of members in the union is obtained.The similarity between the training data set of Swarm A and the validation data set of Swarm B,as well as that between Swarm A and Swarm C,is presented in Table 3.

In Table 4,it is seen that different thresholds result in different similarity measures.When the thresholds for the time difference and angular difference increase,the similarity understandably increases as well.The similarity between Swarm A and Swarm C is always higher than that between Swarm A and Swarm B,indicating the observations of Swarm A and Swarm C are much closer to each other both temporally and spatially,which is favorable to generalize the Swarm A models to Swarm C.It is worth noticing that,in most cases,for a fixed time interval,the increase of angular threshold has no or little effect on the similarity.The higher similarity between Swarm A and Swarm C is understandable,because they are flying almost side-by-side,and the projected distance in the in-track direction between them is about 15 km,thus,the data condition and orbital environment for them are very similar.Different for the Swarm A and Swarm B,the similarity measures are significantly smaller than that between Swarm A and Swarm C,which leads to poorer generalization performance when the Swarm A models are applied to Swarm B.

Table 4Jaccard Similarity between Tracks of Swarm Satellites

The results provide some insights into whether the trained models of a satellite can be successfully generalized to other satellites.If the data of a satellite is temporally and spatially close to the training data,the trained models are more likely to have better generalization performance.In this sense,one may first perform the Jaccard similarity between the training data and application data,and then determine whether to apply the trained models to the application data.

4.7.Another Perspective of the Generalization Capability

Theoretically speaking,if the PEs are accurately described by the PCs at each propagation point,the set of ratios of the errors to the covariances expectations,calculated as Mahalanobis distances,should conform to a chi-squared distribution with 3 Degrees of Freedom(DoF)(Drummond et al.2014).Usually,a Goodness-of-Fit(GOF)test is performed to assess how well the empirical distribution of Mahalanobis distances for each group of trajectories conforms to the expected 3-DoF chi-squared hypothesized parent distribution.Many GOF tests are proposed(Drummond et al.2014;Aristoff et al.2021),among these tests,Cramer von Misses(CvM)is widely used in space community.

In this section,the CvM GOF test is carried out to evaluate the effectiveness of the proposed compensation method.The evaluation procedure starts with the collection of bins of 3-DoF chi-squared statistics at each 60 s propagation point for a group of propagations.Accordingly,the number of 3-DoF chisquared statistics in each bin is equal to the number of trajectories propagated in the group being tested.Ultimately,each bin of 3-DoF chi-squared statistics (at a common propagation point)is tested for realism using the aforementioned CvM test statistic.

Figure 16 shows the empirical and hypothesized parent 3-DoF chi-squared distributions before the trained model of Swarm A was generalized to Swarm C,the red curves represent empirical distributions at each propagation point whereas the blue square-dot curve represents the hypothesized parent distribution.Clearly,the empirical and hypothesized parent 3-DoF chi-squared distributions do not match at all,while in Figure 17 the empirical distributions are conforming much closer to the hypothesized parent distribution after the trained model was generalized to Swarm C.

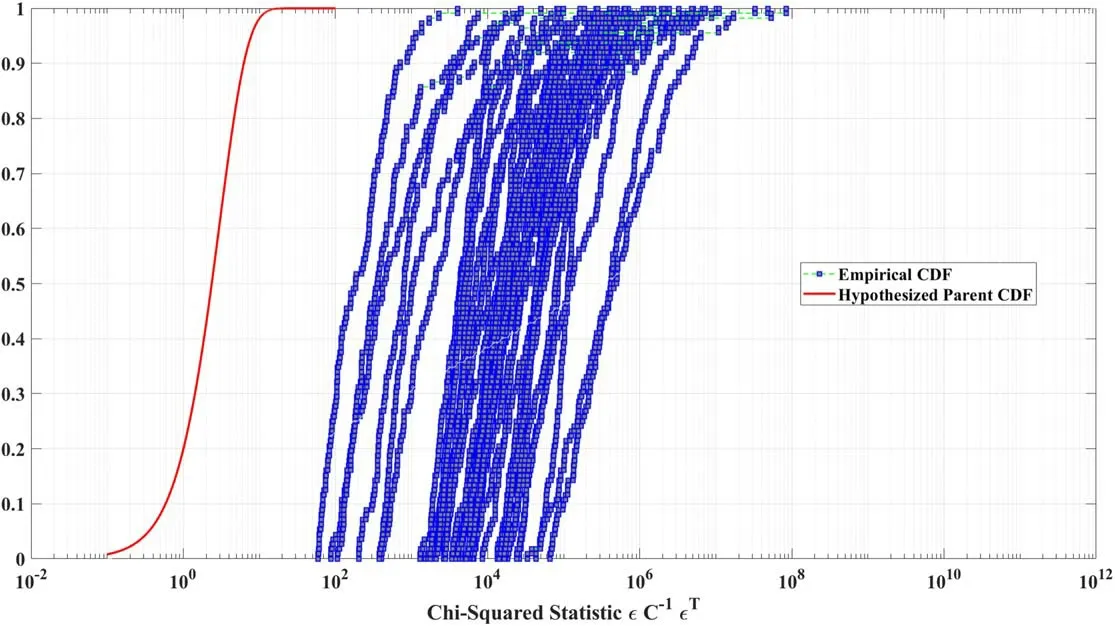
Figure 16.Empirical and hypothesized parent 3-DoF chi-squared distributions (before the trained model of Swarm A was generalized to Swarm C).

Figure 17.Empirical and hypothesized parent 3-DoF chi-squared distributions (after the trained model of Swarm A was generalized to the Swarm C).

Figure 18 shows ap-value versus propagation time bar chart in which eachp-value represents the likelihood the bin of covariances at a particular propagation point conforms to a 3-DoF chi-squared distribution.The red-dot line represents the 1% Confidence Interval whereas the blue bar represents the likelihood the empirical distribution conforms to its parent distribution at a particular propagation point (Sackrowitz &Samuel 1999).The covariance realism assessment in this study collects bins at each 1.5 hr propagation time step over a 7 days propagation timespan.As a result,112 bins are assessed for covariance realism.After the trained model using Swarm A was generalized to Swarm C,55.3%of the set of trajectories during the trajectory propagation timespan conform to a 3-DoF chisquared hypothesized parent distribution.such a figure can be used to determine in which parts of the propagation timespan the covariance realism is faring well and in which it is faring poorly.

Figure 18.p-value versus propagation time bar chart(after the trained model of swarm A was generalized to Swarm C).

It is noted that covariance unrealism,however it may be evaluated,is unlikely consistent over the propagation time in the sense that,if the covariance is realistic at a particular propagation point,it cannot be expected to be realistic at all propagation points.When pursuing covariance realism remediation,one will therefore need to decide whether some sort of omnibus improvement over all propagation points is desired or whether it is preferable to focus on a particular part of the propagation timespan.

For our result,a Pass Percentage of 55.3% is not an ideal result,but a set of covariances produced by the generalized model exhibiting a Pass Percentage closer to 60% is still a significant step forward.

5.Conclusion

This work proposes an alternative approach to achieving better covariance realism of the predicted orbit state.The work has demonstrated the feasibility of using ML methods to capture the difference between the propagated covariance and the orbit prediction errors,and thus,applying the trained models to correct the propagated covariance will result in a more realistic characterization of the orbit prediction errors.Compared with our previous dynamic calibration method (Li et al.2019),the proposed approach in this study is more automatic and general.

The BT and RF methods are implemented in the ML framework to learn the inconsistency pattern when only sparse SLR track data are available in the orbit determination.Using the data in one month as training and testing data,the RF methods can capture more than 98% of the underlying inconsistency pattern.Applying the learned models to the data in the subsequent two months (the generalization to the future),the propagated covariance can be effectively corrected for more than 50% of the inconsistency,resulting in the corrected covariance much closer to the errors of true predicted states.

The performance of applying Swarm A models to Swarm B and Swarm C is also investigated.The generalization of the Swarm A models to Swarm C is more successful than that to Swarm B.Because Swarm A and Swarm C are flying side-byside,about 79%and 64%of the inconsistency of Swarm C can be corrected on average when the Swarm A models are applied.To further explore the behind causes,the Jaccard similarity is introduced to examine the temporal and spatial similarity between the training data and application data.It is found that the Jaccard similarity is a proper metric that can guide one on whether and when is the right time to generalize the trained models of one satellite to another.

Furthermore,a traditional CvM GOF test is performed to evaluate the covariance realism.A Pass Percentage of 55.3%has been achieved,which further demonstrates the effectiveness of the proposed machine learning algorithm in improving the covariance realism.

From an operational perspective,the trained models,once optimized,could be deployed to run alongside traditional methods to perform near-real-time calibration to achieve better covariance realism.Further research is suggested to apply the established ML framework to more tracking data scenarios and more RSOs.

Acknowledgments

This research has been supported by the National Natural Science Foundation of China(grant No.12103035),the Special Fund of Hubei Luojia Laboratory (grant No.230600003),and the Fundamental Research Funds for the Central Universities(grant No.2042023gf0007).The authors are grateful to anonymous reviewers whose constructive and valuable comments greatly helped us to improve the paper.

ORCID iDs