Theoretical Analysis of Random Scattering Induced by Microlensing

Wenwen Zheng ,Hou-Zun Chen ,Xuechun Chen ,and Guoliang Li

1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210023,China;wwzheng@pmo.ac.cn

2 School of Astronomy and Space Science,University of Science and Technology of China,Hefei 230026,China

3 Institute for Frontier in Astronomy and Astrophysics,Beijing Normal University,Beijing 102206,China

4 Department of Astronomy,Beijing Normal University,Beijing 100875,China

Abstract Theoretical investigations into the deflection angle caused by microlenses offer a direct path to uncovering principles of the cosmological microlensing effect.This work specifically concentrates on the the probability density function (PDF) of the light deflection angle induced by microlenses.We have made several significant improvements to the widely used formula from Katz et al.First,we update the coefficient from 3.05 to 1.454,resulting in a better fit between the theoretical PDF and our simulation results.Second,we developed an elegant fitting formula for the PDF that can replace its integral representation within a certain accuracy,which is numerically divergent unless arbitrary upper limits are chosen.Third,to facilitate further theoretical work in this area,we have identified a more suitable Gaussian approximation for the fitting formula.

Key words: gravitational lensing: micro– methods: analytical– galaxies: stellar content

1.Introduction

The strong lensing effect caused by a foreground galaxy may produce multiple macroimages,and in the mean time,the compact objects inhabiting the galaxy can further deflect the light rays,causing a macroimage to split into microimages.This phenomenon is known as the cosmological microlensing effect and was described by Chang&Refsdal(1979).Although it is extremely difficult to directly distinguish microimages,the flux anomaly between macroimages can provide a clue,because light rays from different macroimages are affected by different distributions of microlenses.It is possible to detect this effect in a time-domain observation: The relative motion between the background source,the lens galaxy,the randomly moving stars and the observer induces differences between light curves of macroimages (when other impacts are deducted),which was first confirmed in quasar system Q2237+0305 presented by Irwin et al.(1989).Based on the theory of microlensing,the variation of light curves can contain information on both the source size and the lens mass distributions.This has led to a series of pioneering research efforts on constraining the inner structure of quasars (Kochanek 2004;Mortonson et al.2005;Sluse et al.2012) and the mass distribution of compact objects in the lens galaxy(Wyithe&Turner 2001;Mediavilla et al.2009;Schechter et al.2014;Jiménez-Vicente &Mediavilla 2019).These research efforts have quickly produced significant results.In recent years,a host of unprecedented events has been observed,where individual stars at cosmological distances are magnified to an extreme degree due to their close proximity to massive cluster caustics (Kelly et al.2018;Rodney et al.2018;Chen et al.2019;Kaurov et al.2019;Diego et al.2022;Welch et al.2022).The smooth macrocaustic will be broken into a net of microcaustics in the presence of intra-cluster light (ICL) in clusters,as described in Venumadhav et al.(2017),inducing a variety of fluctuations in the magnification of a star as it moves across the microcaustics.Similar to a lensed quasar system,microlensing light curves also provide the possibility of digging information about the size of the source star,the fractions of ICL and even MACHOS.Therefore,extracting the information contained in the light curves is essential in microlensing studies,and simulations have become the most commonly used method thanks to the vigorous development of computer technology.

Several approaches have been developed for generating microlensing light curves,with the most commonly used method being inverse ray shooting (IRS) (Kayser et al.1986;Schneider &Weiß,1986).Since then,various optimized versions of the IRS method have been proposed (Wambsganss 1999;Mediavilla et al.2006;Thompson et al.2010;Shalyapin et al.2021;Zheng et al.2022).They share a basic procedure: light rays are traced back from the image plane to the source plane to generate a magnification map,which is then convolved with a moving source to produce a set of light curves.However,the processing of huge amounts of data still poses a great challenge for standard simulations when dealing with caustic-crossing events.New methods,such as those proposed by Meena et al.(2022) and Diego (2022),have been developed to reduce computational costs while still achieving accurate light curves.Additionally,for point sources,there are other methods(Lewis et al.1993;Witt 1993)that are designed to directly produce individual light curves without generating a whole magnification map.

Nonetheless,all of these approaches face a common challenge: the presence of compact objects can cause some of the light rays to be deflected out of the source plane,leading to a loss of simulation accuracy.To address this issue,the size of the shooting area needs to be increased when setting the image plane in order to ensure precision (Schneider &Weiß 1986,Wambsganss 1999).It is important to note that the size of the increased shooting area should be determined based on the distribution of the microlens-induced deflection angle.This distribution is directly related to the magnification and observable variation in the lensed source light curves,which can provide valuable insight for future theoretical research(Dai&Pascale 2021).Therefore,further study on microlensing deflection angle is necessary.

Remarkable results were presented in Katz et al.(1986)(hereafter K86),where the integral form of the probability density distribution of the deflection angles is given in detail(their Equation (13)).K86 concluded that the probability density function(PDF)has a Gaussian form at small deflection angles and is inversely proportional to the quartic of deflection angle at the infinite end.This provides a basis for all types of methods that include an “image-to-source-plane ray mapping”part to set a buffer to control missing light rays.

In our previous simulation work (Zheng et al.2022),we included a “negative mass sheet” term in the deflection angle equation,which led us to reanalyze the PDF of the deflection angles.Our new analysis yielded a different result that showed better consistency with our simulation.This paper is organized as follows:In Section 2,we present the theoretical derivation of the PDF of the deflection angle.This section is divided into three subsections: In subsection 2.1 we re-deduced the PDF of the deflection angle.Subsection 2.2 describes the process of obtaining a fitting formula for the PDF and in subsection 2.3 we present the methods we used to obtain a Gaussian approximation.A short summary of this work is provided in Section 3.

2.Probability Density Function of the Deflection Angle

Ideally,in the absence of compact objects,all light rays traveling from an image rectangle with a side length ratio of|1 −κ −γ|/|1 −κ+γ|would fall within a square.However,the presence of compact objects causes some of the rays to scatter out,indicating the effect of the deflection angle induced by microlensing.Referring to our previous work Zheng et al.(2022),the general form of the deflection angle can be written as

where θ and θidenote the light positions and lens positions on the image/lens plane,respectively.N* is the number of microlenses(hereafter stars,as they are the majority in number)whilemidenotes their mass.κ is the dimensionless surface mass density of the mass sheet (which contains both the compact and smooth mass)and γ is the external shear;both are derived from the strong lens model.

The general form of the deflection angle can be written as a sum of three terms.The first term represents the impact of local convergence and shear.The second term indicates the contribution from the individual stars,with the mean surface mass density of κ*,whereas the third termα κ−*represents a negative mass sheet that is only composed of smooth matter,with the same κ* value to cancel out the redundant mass from the second term.Thus,the sum of the second and third terms represents the perturbation caused by compact objects.This perturbation will be the deflection angle we mainly focus on in this work.

2.1.PDF of the Deflection Angle

In K86,the integral representation of scattering PDF has the form (their Equation (13)),

where φ denotes the deflection angle,and J0is the Bessel function of the first kind.x=φ/φ0and φ0is a scaling parameter that is related to the number of microlensesN,as will be explained in detail later in the text.

However,in their approach,they only considered the deflection angle contributed from the individual stars,so the negative mass sheet was taken as an overall variable.Consequently,in every situation,the negative mass sheet occupied by each star will not overlap.In contrast,we assume that each star carries a negative circular mass sheet with radiusR,and that the two parts of each star have equal and opposite masses,resulting in a net zero mass.This means that both parts act as a scattering source when calculating the deflection angle.In this situation,the negative mass sheets of the scattering sources may overlap depending on their distance,which we consider to be a more natural scenario for random scattering of microlensing.

Then for one scattering source,the deflection angle at impact parameterb(b≤R) is

and for more details on this part of the derivation please refer to Appendix A.

Equation (9) has the same form as the one derived by K86,which has been modified from 3.05 to 1.45.Figure 1 displays a comparison between Equations (8) and (9),along with the deviations caused by the different numerators.Here we find that Equations (8) and (9) are in good agreement,which indicates that the approximations used are reasonable.On the other hand,the difference brought by the two numerators is non-negligible.

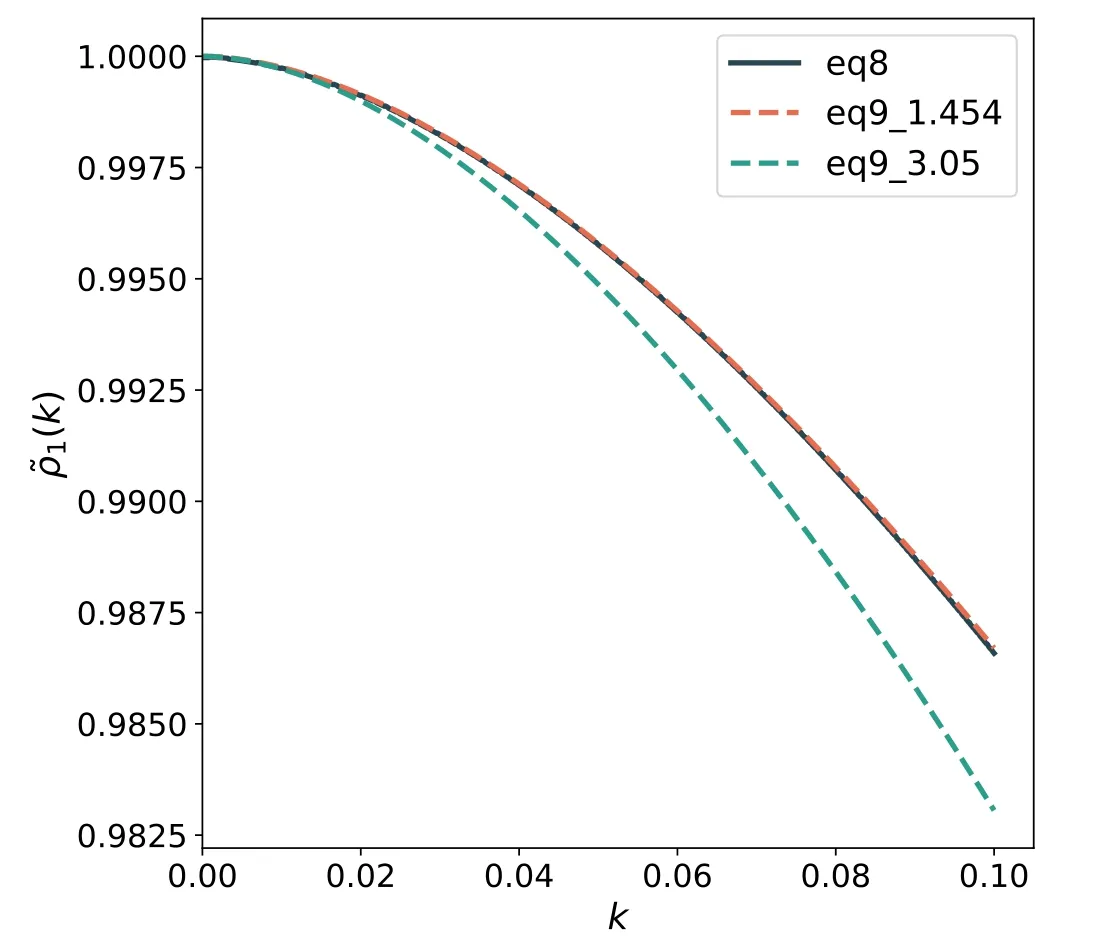
Figure 1.The comparison of Equations (8) and (9).The dark blue solid line represents the numerical solution result of Equation(8),while orange and green dashed lines correspond to Equation (9) and the result of K86,respectively.

Suppose there areNstars with uniform mass randomly distributed in a circular plane with radiusR.We choose a circular plane,rather than a rectangular one,for ease of calculation,which will not lead to a different result.Each star and its corresponding negative mass sheet occupy a circular area with radiusR0=.

Hence,the final scattering angle distribution is to repeat the convolution operation of ρ1(φ)Ntimes.In Fourier space we have This is the integral representation of the scattering PDF in terms of our negative mass sheet model.Not surprisingly,it has the same form as Equation(2)except for the coefficient 1.454.

In Figure 2 we compare the numerical results (dashed lines)of Equations(12)and(2)(K86,Equation(13))with a series of simulation results (solid lines) obtained using our GPU-PMO code (Zheng et al.2022).The PDF of the deflection angle is calculated with a varying number of lenses (from 102to 107)signified by different colors in Figure 2.Only 102,103,104and 106are shown in the figure for clarity.The numerical result for Equation (2) is plotted in the left panel while that for Equation (12) is in the right panel.The deflection angle is scaled by φ0.As affirmed in Figure 2,our modified equation,Equation (12),fits the simulation results better compared to Equation (2).This suggests that our assumption and derived new coefficient of 1.454 are reasonable.

Figure 2.The probability density distribution of the deflection angle.Solid lines represent the distribution realized by our simulation,dashed lines represent the numerical results of Equation (2)concluded by K86 (left) and the newly acquired Equation (12)(right).The star mass is uniformly distributed with M=1 M⊙,and different colors stand for deflection angle distributions with different numbers of stars: 102,103,104 and 106.

2.2.The Fitting Formula for Deflection Angle Probability Density Function

As mentioned in K86,the limits of the integration of Equation(2)cannot run from 0 to ∞,otherwise it will lead to a formal divergence.Therefore,in practice,K86 terminates the integration when the integrand becomes exponentially small.They calculate the asymptotic limits for Equation (2) and conclude that for small φ,the density is a Gaussian,and for large φ,it is inversely proportional to the fourth power of the deflection angle.

In this work,we attempt to obtain the analytic result of Equation (12) rather than rely on the asymptotic limits.

First,we definet=φ/φ0,replace the coefficient 1.454 with the parameter β,and defineσ2=ln(β),to rewrite Equation (12)

By inserting Taylor expansion

The specific process of solving these two integrals is described in Appendix B,here we jump to the result

and for the infinite end,Ei(z)has an asymptotic expansion state as

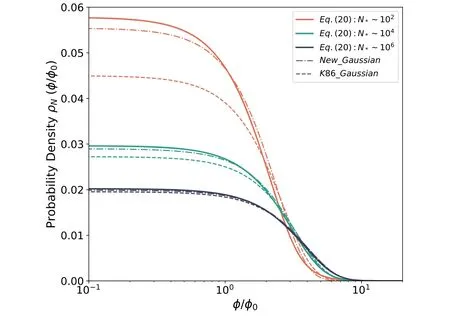
Theoretically,series (19) does not converge for a fixedz,therefore,the asymptotic series needs to be cut off before the term becomeszn

Altogether,we obtain the fitting formula of the PDF

To investigate the behavior of the fitting formula (20) at large and small scattering angles,we insert the series(18) and(19) into the fitting formula and take the limitt→0,t→∞.

For φ ≪φ0,i.e.,t→0,we find

For φ ≫φ0,i.e.,t→∞we infer that

and this result is generally consistent with that in K86.

In addition,the normalization of the fitting PDF given by Equation(20)is required,and we prove that it has already been normalized to unity.This part is described in Appendix C.

We examine Equation (20) by comparing its solution with numerical results of Equation (12) and the simulations,as sketched in Figure 3.Solid lines are simulation results (left panel) and numerical results (right panel) of Equation (12),while dashed lines are the solutions of Equation (20) in both panels.It can be concluded from the figure that the fitting PDF,Equation(20),is reliable,and its numerical solution is in good agreement with both the simulations and the numerical results of Equation (12).

Figure 3.Comparison between the simulation (solid lines in left panel),Equation (12) (solid lines in right panel) and Equation (20) (dashed lines in both panels).Different colors stand for the deflection angle distributions with different numbers of stars:102,103,104 and 106,which are uniformly distributed with M >=1 M⊙.

Furthermore,we expand our result to microlenses with a mass spectrum,along the path of K86.The PDF for a nonuniform mass distribution could be described as

According to the convention above,we also verify the validity of Equation (23) and Equation (24),similar to Figure 3,as presented in Figure 4.A Salpeter mass distribution with the mass range from 0.1M⊙to 10M⊙resulting in 〈M〉=0.3M⊙is chosen in our realization.Notably,here in Figure 4 the deflection angle is scaled with.Good consistency can be drawn from both the left panel and the right panel indicating the reliability of Equation (23) and Equation (24).

Figure 4.The probability density distribution of the deflection angle with a Salpeter mass distribution.Solid lines represent the distribution realized by our simulation(left)and the numerical result of Equation(23)(right),while dashed lines signify the numerical result of Equation(24).The star mass follows a Salpeter distribution,and the mass range is from 0.1 M⊙to 10 M⊙,leading to 〈M〉=0.3 M⊙.Different colors stand for different numbers of stars: 104,105,106 and 107.

Figure 5.The comparison of the approximate k and the real k(top)and relative error of (bottom).Two vertical gray lines signify the value of σ when N=102 and N=109,respectively.The horizontal gray line in the bottom panel marks the relative error of equaling 1%.

Figure 6.The comparison results of the fitting formula Equation(20),the new Gaussian distribution and the Gaussian distribution from K86;the x-axis is logarithmic.The red,green and blue lines stand for the situation with 102,104 and 106 stars in the uniform mass.

2.3.Gaussian Approximation of the Fitting Formula

In the previous section,we obtained a fitting formula for the integral form of the probability distribution for microlensing induced deflection angle.Nevertheless,in order to simplify the following theoretical derivations,we aim to find a suitable Gaussian approximation,which is suggested by the central limit theorem applied to multiple deflection distributions that are dominated by small angles.Given the deviations between Equation (2) and our fitting formula and the simulations mentioned before,the Gaussian distribution obtained by K86 may not be the best approximation for our fitting formula.

Assuming that the standard deviation of the new Gaussian distribution is σn,we can use chi-squared as a measure to find a suitable σnfor the fitting formula(20).

We define χ2as

From solving the integrals on both sides of the equation we acquire

Despite a complex solution for this cubic equation having been obtained,we decide to replace it with an approximate but more concise form

3.Summary

The cosmological microlensing effect can be induced by the existence of compact objects in the lens plane,leading to observable stochastic variations in the fluxes of the lensed sources.In order to improve our understanding of this effect and facilitate further analytical research,it is necessary to reexamine the microlensing deflection angle.We calculate the PDF of the light deflection angle using a more appropriate assumption and obtain an integral expression that has better agreement with the simulation results.Moreover,through mathematical deduction,we obtain a fitting formula for this integral expression,which allows for the direct and almost accurate calculation of the deflection angle probability density distribution.In addition,we find a more suitable Gaussian approximation for this fitting formula,which can simplify subsequent theoretical work.

Acknowledgments

The authors thank the anonymous referee for helpful comments.This work is supported by the National Natural Science Foundation of China (NSFC,Grant Nos.U1931210,11673065 and 11273061).We acknowledge the cosmology simulation database (CSD) in the National Basic Science Data Centre (NBSDC) and its funds the NBSDC-DB-10 (No.2020000088).We acknowledge the science research grants from the China Manned Space Project with No.CMS-CSST-2021-A12.

Data Availability

This theoretical study does not generate any new data.

Appendix A The Derivation of Equation (8)

For Equation (8) ata≪1,we make some deductions by integrating it by parts and using some basic properties of a Bessel function:

noting that F(0)=1.

For smalla,the Taylor series of the J1state is

Since expanding Equation(A2)should be valid for some finite area,i.e.,0

Then we expand the function of α near infinity

Theoretically,we expect the value ofsshould be very close to 1.8412,which is the first root of transcendental equation J0(x)=J2(x).Further numerical test suggests thats≃1.866 is a better choice,which gives

Appendix B The Derivation of Equation (15)

The first integral formula of Equation (15) is a special case(l=1) of the following result

Equation (B1) can be derived by inserting the Taylor series of J0into the left integral,and exchanging the integration and summation.

Forl=1,we have

To deal with the second term in Equation (15),we take the derivative oflon both sides of Equation (B1) and letl=3,

Appendix C Normalization of the Fitting Probability Density Function

We will prove that the fitting PDF given by Equation (20)has already been normalized to unity.Here,we list two basic integral formulas,

Combining them with the series (18),by straightforward practice we have