A Number Estimate of Detectable Detached Black Hole-star Binaries using a Photometric Telescope

Zhe-Cheng Hu,Yan-Lv Yang,Yuan-Hao Wen,Rong-Feng Shen,and Pak-Hin Thomas Tam

1 School of Physics and Astronomy,Sun Yat-sen University,Zhuhai 519082,China;huzhch6@mail2.sysu.edu.cn,shenrf3@mail.sysu.edu.cn,tanbxuan@mail.sysu.edu.cn

2 CSST Science Center for the Guangdong-Hong Kong-Macau Greater Bay Area,Zhuhai 519082,China

Abstract Detached and wide-orbit black hole-star binaries(BHSBs)can generate three types of periodic photometric signals:Ellipsoidal Variation,Doppler beaming and Self-Lensing (SL),providing a proxy to discover these black holes.We estimate the relative amplitude of the three signals for such systems and the detectability for black holes of a photometric telescope like Kepler in several steps.We estimate the searchable star number by assuming every star has a black hole companion,and apply the occurrence of BHSBs in field stars to estimate the detectable black hole signals.We consider three types of Initial Mass Function(IMF)model with different high end exponential slopes.“When spot and white noise are both considered,there is about one detectable signal for SL and less than one event is expected for beaming and Ellipsoidal Variation signal in Kepler Input Catalog stars with the standard IMF model.”to“Due to contamination by stellar spots and white noise,one may expect one detectable signal for SL and less than one detectable signal for both beaming and Ellipsoidal Variation in Kepler Input Catalog stars with the standard IMF model.”On the other hand,if we assume that only white noise affects the detection efficiency of the BHSBs,we expect about 10 Ellipsoidal Variation signals and 17 beaming signals to be detectable while the number of SL signals remains unchanged.

Key words: black hole physics–techniques:photometric–surveys–stars: black holes–stars:variables: general

1.Introduction

Black holes (BHs) are compact objects that no particles or even light can escape from within its event horizon.Standalone BHs emit no light,making them invisible.However,we may detect BHs indirectly in a black hole-star binary (BHSB)system which contains a BH and a visible (companion)star.If the companion star fills its Roche lobe and mass transfer emerges,we call such system a close BHSB.Otherwise we call it a detached BHSB.So far,the confirmed stellar-mass BH candidates are mostly found from X-ray surveys rather than photometric observations(e.g.,Casares 2007;Fender et al.2013).This is because according to the blackbody radiation law,an object needs to be at above 103Now at Department of Astronomy,Tsinghua University,Beijing 100084,China.K to radiate X-rays(Remillard &McClintock 2006).If there is a close BHSB and thus the BH has an accretion disk,the gravitational energy of the accretion matter will transfer to kinetic energy of particles,which is the internal energy of the accretion disk,thus it will reach the temperature above 104Department of Astronomy,School of Physical Sciences,University of Science and Technology of China,Hefei,230026,China.K and radiate X-rays.Such a deep gravitational well can only be provided by a compact object—BH or neutron star (NS).It is therefore clear that X-ray observations more likely detect close BHSBs or NSstar binaries,which only constitute a small fraction of the overall population.

According to the simulation of Wiktorowicz et al.(2019),the number of wide-orbit BHSBs can be about 10–105National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China.times of that of close BHSBs in the Galaxy.Wide-orbit here means that the companion star does not fill it Roche Lobes.Observations of massive binary systems in the field(Sana et al.2012),i.e.,the systems containing at least one O/B-type star,show a similar picture.Clearly,there are a lot detached BHSBs remained to be unveiled.

The very weak or no mass transfer of detached and wide BH binaries causes them to be X-ray quiet or weak.Therefore,one needs to rely on the orbital modulation of companion’s brightness by the BH to detect them.The three types of signals are Ellipsoidal Variation (EV),Doppler beaming and Self-lensing (SL).The EV signal is mainly caused by stellar tidal distortion due to the gravity of the BH(Morris &Naftilan 1993;Shporer 2017;Gomel et al.2021).Doppler beaming also affects the brightness of the star,which contains three parts of effect: Doppler shift,light aberration and time dilation caused by the orbital motion of the companion star(Loeb &Gaudi 2003;Shporer 2017).SL signal manifests itself as a sudden increase in flux when the BH moves in front of the companion star,due to gravitational lensing(Sahu &Gilliland 2003;Rahvar et al.2011).These three types of photometric signals are nicely summarized by Masuda &Hotokezaka (2019).

Besides normal BHs,mass-gap BHs have masses between 3M⊙and 5M⊙(Fryer et al.2012).The 3M⊙is the upper limit of the NS (Özel &Freire 2016).So the least massive BH should be more than 3M⊙,but most BHs are found with mass larger than 5M⊙,which is the reason for so-called mass-gap BHs.The existence or not of mass-gap BHs and their number is important to understand star evolution and core-collapse supernova mechanism(Jayasinghe et al.2021).The photometric signal can also be produced by mass gap BHs in binaries.Some candidates of mass-gap BHs have already been found(e.g.,Thompson et al.2019;Jayasinghe et al.2021) by combining radial velocity and photometric measurements.

In recent years,space-based high-precision photometric telescopes like Kepler/K2(Borucki et al.2010) and TESS(Ricker et al.2015) have been used to obtain millions of high quality light curves(i.e.,down to a precision of ∼100 ppm and even below) over a month to years.These light curves allow the search of BHSBs from a huge number of stars in a way that could not have been done before.Kepler has a field of view of 115 square degrees and monitors about 105stars with 9–15 mag in the optical band.TESS is a survey mission,which aims to observe more than 107bright stars and find those who show transits.The TESS stars typically have a magnitude of 4–13 in theIcband.The observing time of stars in the TESS survey varies from a month to a whole year.In this work,we estimated how many BHSB photometry signals could have been/would be found by a telescope like Kepler.While the Kepler mission and TESS mission differ somehow from each other,using the Kepler capabilities one gets the number of searchable BHSBs that can be applied to other planet-searching mission similar to Kepler,e.g.,Earth 2.0.

Previous studies have used Kepler and TESS photometric data in their searches of compact objects.Many focus on the EV effects,resulting in the discovery of new or detection of some known compact object systems(Yu et al.2019;Pal et al.2020).Rowan et al.(2021) report more than 300 EV signal candidates from the ASAS-SN survey;those are good sample to be followed by future observations.Studies to search for Doppler beaming signals are also in place(Faigler et al.2015).SL signals have been used to discover at least four wide-orbit white dwarf systems(Kruse &Agol 2014;Kawahara et al.2018;Masuda et al.2020).Masuda &Hotokezaka (2019,hereafter MH19) systematically describe the potential photometric signals in searching BHs using TESS,and estimate an order of 104BHSB signals.In this work,we focus on the Kepler field and the Kepler Input Catalog (KIC) stars,taking into account binary interaction in the field binary model,which has not been considered by MH19.

This paper uses the Kepler sample to study the detectability of BHSBs due to the following reasons.The Kepler sample has higher photometric and positional precision compared to the TESS sample.Besides,the field of view and the observing strategy is different for these two missions.As a result,both samples are unique and complement one another in the examination of planets,stars,and compact objects.Additionally,the Kepler field has receive significant attention from a diverse range of researchers over the past decade,leading to numerous survey telescopes,such as APOGEE (Fleming et al.2015) and LAMOST (De Cat et al.2015),dedicating time to observing stars in the field.This has generated a wealth of archival data that can be further augmented by a focused detectability study of the KIC sample.

Apart from estimating the number of above-mentioned signals that could have been detected using the original fouryear Kepler mission,this paper also serves as a preparatory work for the ET project(Ge et al.2022) and other similar planned projects,to detect compact objects.ET project is a ultra-high-precision photometric survey mission,temporarily named “Earth 2.0 (ET).” This mission plans to stare at the direction that encompasses the original Kepler field for four continuous years.Besides,it is also an ultra-high-precision photometric survey mission,which is quite similar to the Kepler mission.These are the two main reasons why this work focus on the Kepler field and the KIC stars.

The structure of the paper is as follows:in Section 2,we first show the relation between relative signal amplitude and system parameters.We then show the method in Section 3,in which we first estimated the number of detectable stars if every star in the Kepler Input Catalog(Mathur et al.2017)would have a BH companion in Section 3.1 and calculated the number of detectable BHSBs with three different Initial Mass Function(IMF) models in Section 3.3.The presentation of results is in Section 4 and discussion is presented in Section 5.We conclude in Section 6.

2.Photometric Signals of BHSBs

Three types of photometric,periodic signals could be produced by a compact binary system,which are EV,Doppler beaming and SL,see Masuda &Hotokezaka (2019) for a nice presentation.When the binary orbit is viewed edge-on,all three signals will have the largest amplitude,while the SL signal has the strictest limitation on the orbital inclination with respect to the line of sight(LoS)than the other two.The simulated signal for an edge-on system with an orbital period of four days,a black hole massM•=10M⊙and a companion massM⋆=1M⊙is shown in Figure 1.

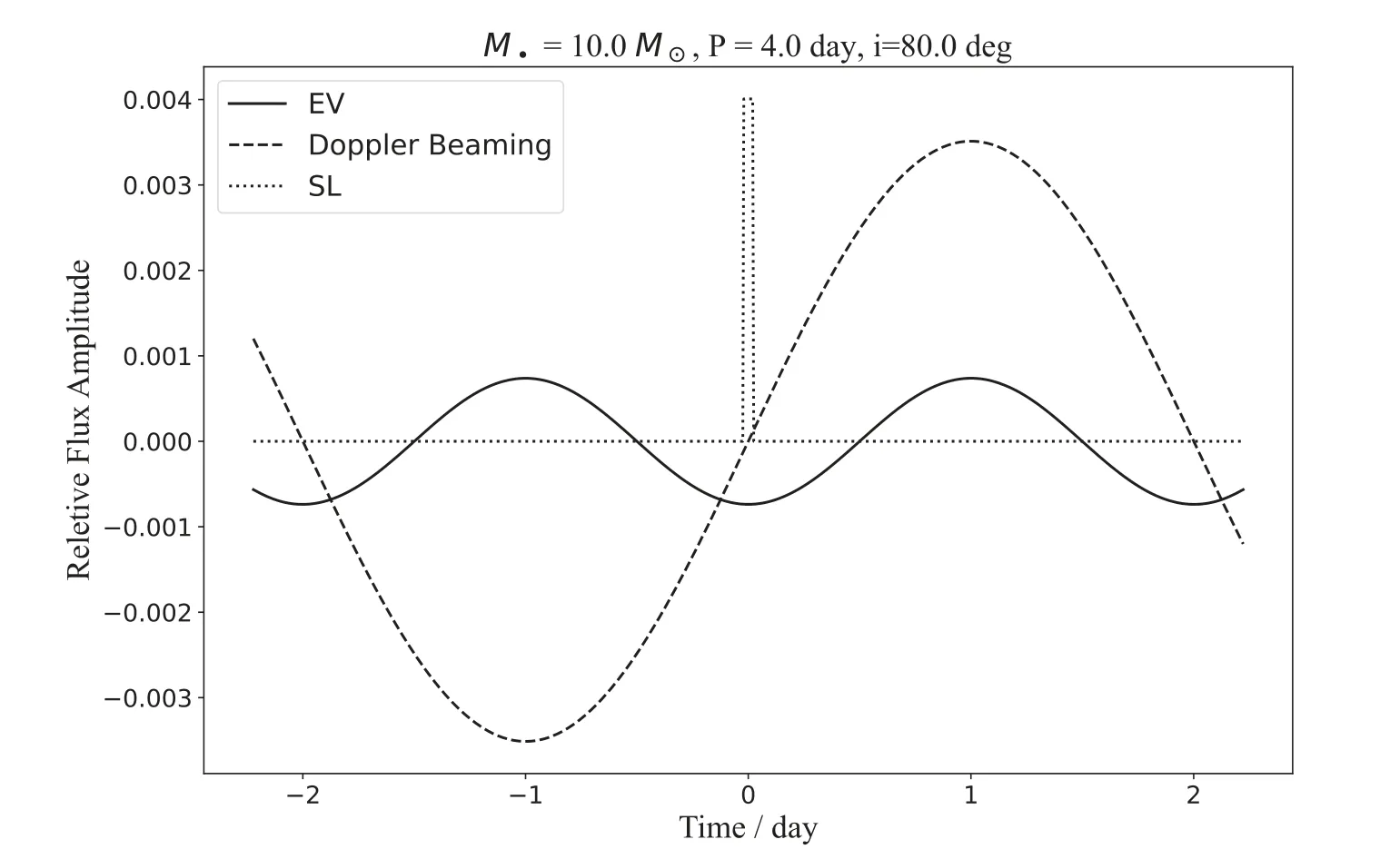
Figure 1.Modeled modulation of the three kinds of photometry signals.The solid line represents the EV signal,the dashed line represents the beaming signal,and dotted line represents the SL signal.

In this section,we quantitatively describe the three kinds of signals and show their relative amplitude ΔF/F⋆,in which ΔFis the amplitude of periodic flux modulation andF⋆is the average flux of that star.6Stellar flux does vary,but for the first approximation we assume here that such a variation is small compared to,or can be separated from,the above three kinds of signals related to the gravity of the compact object.We assume a circular orbit for simplicity.

2.1.Ellipsoidal Variation

When the visible star is tidally distorted by the gravity of the compact companion like BH(Gomel et al.2021),the star is roughly shaped into “a water drop,” thus changing the projected surface area (on the celestial sphere) of the visible star along the orbit.When the star and compact object lie nearly at the same LoS (say,at phase zero and 180°),the observed area is around the smallest.When the visible star is at one side of the compact object (i.e.,at phase 90° and 270°),the observed area of the star is around the largest.So if the orbital inclinationi=0,the observed area would not change at all,then the EV signal vanishes.The EV signal has the most dominant period which is half that of the orbital periodP.With a smaller orbital period,the EV signal will become larger,because the tidal distortion is also larger.

The relative amplitude,which is the modulation amplitude versus the companion star luminosity,is given by(Morris &Naftilan 1993):

whereR⋆and ρ⋆is the radius and density of the companion star.ais the physical separation between the objects in the binary.αevis a factor depending on the gravity-darkening coefficientgand limb-darkening coefficientu:

Here we set αev=1 for simplicity,which is reasonable according to Gomel et al.(2021).

2.2.Doppler Beaming

Light from a star moving with certain speed relative to the observer will be Doppler-shifted,which also lead to the change in bolometric flux.This change is the main reason of the Doppler beaming effect(Loeb &Gaudi 2003).Other effects such as time dilation and light aberration also contribute to the Doppler beaming effect.This effect will make the star becomes brighter when it moves toward the observer and vice versa.The period of flux variation caused by the beaming effect is the same as the orbital period,resulting in a phase curve as shown in Figure 1.If EV signal and Doppler beaming signal are both detected with respective period and phase,it can help to confirm the binary nature of the source.

The relative amplitude induced by the beaming effect can be described as:

where αbeamdepends on the spectral characteristics of the companion star:

where ν is a selected frequency andFνis the spectra of the companion star.

Here we set αbeam=1,for a convenient calculation,which is reasonable for a solar-like star (Shporer 2017).

2.3.Self-lensing

The SL signal is caused by the effect of gravitational lensing(Schneider et al.1992).When the star,compact star and observer are almost in line and star is behind its compact companion,gravitational lensing happens.As the lens and the lensed object are in the same binary,it is called self-lensing.SL has a strict requirement of the orbital inclination:cosi<⋆a,i.e.,the projection in the direction of view of the compact star must be within the boundary of the star.Unlike microlensing and other types of gravitational lensing,the limitation of orbital inclination is based on star radiusR⋆rather than Einstein radiusRE(Rahvar et al.2011) which is:

whereGis the gravitational constant andcis the speed of light.

When the star and compact object are nearly at the same distance to the observer (i.e.,for the case of a binary),the angular size of the star is much bigger than that of the Einstein radius.The SL signal can be seen as a sudden magnification in brightness,so we use a step function to represent the SL light curve for the first approximation.

The relative amplitude of the SL signal is estimated as:

and the duration time of the signal is(Masuda &Hotokezaka 2019):

3.Method

We first calculate the number of stars for which the three kinds of signals with certain BH massM•and orbital periodPare detectable,assuming every star has a BH companion,withM•andPfollowing a certain density distribution.This is regarded as the number of searchable stars.As a next step,we calculate the possibility of each star to be in a BHSB system.By multiplying these two numbers together,we get the density distribution of detectable BHSBs in the field.We assume that all stars are main sequence (MS;and respective mass–radius and mass–luminosity relations are used) and ignore that about 10%stars in the KIC are actually giants.In reality,the number of detectable EV signals (when giants were considered) would be slightly higher than the more conservative values calculated below due to the lower surface gravity of giants,i.e.,higher fractional flux variability.

3.1.Treatment of White Noise

We use the KIC (Brown et al.2011) to generate searchable stars in the Kepler field of view.7Stars within the Kepler field of view but not in the KIC (generally dimmer than those in the KIC)could also generate detectable signals and our estimates of detectable signals below provide a lower limit.To get the number of searchable stars i.e.,N⋆,we need to estimate the maximum searchable distancedmaxfirst,which is calculated by comparing the relative amplitude of all three kinds of the signal with the noise of the Kepler at a signal-to-noise ratios(S/Ns)of 10.The number of the stars withindmaxis regarded asN⋆.

We estimate the noise level in the Kepler data by using the combined differential photometric precision(CDPP;Christiansen et al.2012),which is a function of noise and stars’magnitudes for a certain instrument,of Kepler.The lower envelope of 15 hr CDPP is used.This is then applicable to data with longer time spans.An upper limit of 16 on the stellar magnitude is also applied because the stars dimmer than 16 mag usually has much larger CDPP value than those which is brighter.The stars with magnitude larger than 16 only contribute to 3% of the KIC stars.The CDPP data points are binned with bin size of 0.1 mag.The bottom 0.3% points with the smallest noise in each magnitude bin are used to generate the lower envelope of the CDPP plot,assuming the following functional form.The best-fit formula is as follows:

while the data points and best-fit curve are shown in Figure 2.

Figure 2.The best-fit curve of 15 hr CDPP of Kepler.The x-axis is the Kepler magnitude,whose wavelength range is 420 nm<λ<890 nm(Brown et al.2011).The gray points are raw cdpp data points and the black points are the 0.3%smallest data points in each bin.The red line is the best fitting fitting curve,which describes the lower envelope below 16 mag quite well.

We bin all the stellar masses from KIC into bins with equal bin size of 0.1M⊙.The original mass for stars in each bin is replaced by the bin’s median value as representative to calculate relative amplitude of each signal with different BH massM•,orbital periodPand orbital inclination anglei.The mass–radius relation according to Demircan &Kahraman(1991)is applied to getR⋆to calculate the relative amplitude of EV and SL signal,which is:

In calculation of the CDPP noise,the stellar magnitude is calculated with a mass–luminosity relation according to Eker et al.(2015):

in addition to the stellar distance.

Once we get the relative signal amplitudeAs(M⋆,M•,P,i),and CDPP noisen(dmax,M⋆),we can solvedmaxthrough the equation below:

Then the number of searchable starsN⋆without the consideration of stellar activity is obtained by counting the number of stars in KIC with in the max searchable distancedmax.

3.2.False Signal from Stellar Activity

EV and beaming signals are both sinusoidal-like.Stellar spot can also produce similar signals.Due to unevenly distributed spots on the stellar surface,the spin of a spotted star can produce a sinusoidal-like signal modulated at the spin period.If the binary is tidally locked,the spin period of the binary would become the same as the orbital period of the binary,which makes it harder to separate the BHSB signals and the spot noise.Actually those EV/beaming BHSBs signals can be detectable (having imprints in the data),but not distinguished from spot noise(having larger amplitude;spotted stars are also numerous as well).Fortunately,the amplitude and the phase of the spot noise are not fixed over a longer time.Therefore,with data over a long-enough time span,one could in principle separate the spot noise from the BHSB signals(Yu et al.2019).

Here we use data from McQuillan et al.(2014) to estimate the level of stellar spot noise in KIC,which contains 34,030 spotted stars.We binned the spot noise data into the same bins as the BHSB signal data in the stellar mass axis and the rotation period axis.Note that we assume that all detectable BHSBs are tidally locked to not underestimate the influence of the spot noise,so the rotation period axis is the same as the orbital period axis in our estimation.The spot noise data are incomplete,i.e.,some stellar mass and the orbital period that we consider are out of the range in which the spot noise data are available.In general,spot noise tends to be larger for smaller stellar mass and shorter orbital period.For those mass and period where no stellar spot measurements are available,the spot noise is assumed to be the same as that in the neighborhood bin.We have verified that the total number of searchable stars is not sensitive to this extrapolation detail.

We consider three threshold levels of BHSB signals:the top 0.1%,1% and 10% of the spot noise.Only when a signal amplitude is larger than the thresholds can we treat that as a searchable BHSB signal.If a signal larger than the threshold is detected,its source could be due to the most active stars or the BHSBs.With the three threshold,the false positive rate is about 34 most active stars out of the KIC sample with 0.2 million stars,which leads to the false positive rate of 10−4.The false positive rate for threshold of top 1%and 10%spot noise is then 2×10−3and 2×10−2.

MH19 investigated the false positive rate for SL signals.They cut the actual light curves of spotted stars from the Kepler mission and added white noise to mimic the TESS light curve.Then the SL signals with the same period as the spot noise are injected into the light curve.Then show that by using box leastsquares algorithm,100% signals forP=0.8–4.8 days can be successfully recovered,and the recover rate is ≈90% forP=0.3–0.8 day andP=4.8–11.9 days,and ≈20% forP=11.9–30 days.As the noise level is higher in MH19,it is not an over estimate to simply apply the result of MH19.The corresponding false positive ratio is no larger than 10−7.As for the false positive rate for SL signal,we apply the result of MH19,which is tested in samples with higher noise level and is 10−7.

To get the distribution of number of searchable stars againstM•andP,we integrate the number of the searchable stars,i.e.,N⋆,with companion star massM⋆and orbital inclinationi.The integration over different stellar mass was done numerically by adding the distribution of different mass groups together.The orbital inclination is integrated assuming that the probability of the direction of the orbital axis is equal in every unit solid angle.Thus we can get the probability distribution against orbital inclination:ρ(i)=siniwhereiis from 0 to π/2.Finally,we getN⋆as shown below:

The result of the integrated searchable star numberN⋆of all three types of stars after considering both white noise and stellar activity noise is shown in Figure 3.The EV and beaming signal results are in the top left and top right panels.These two signals,especially the beaming signal,do not show a smooth change in the distribution of searchable star numbers,which is mainly due to the influence of stellar activity.The spot noise severely affects the number of detectable BHSB signals for these two types of signals as shown in Figure 5.

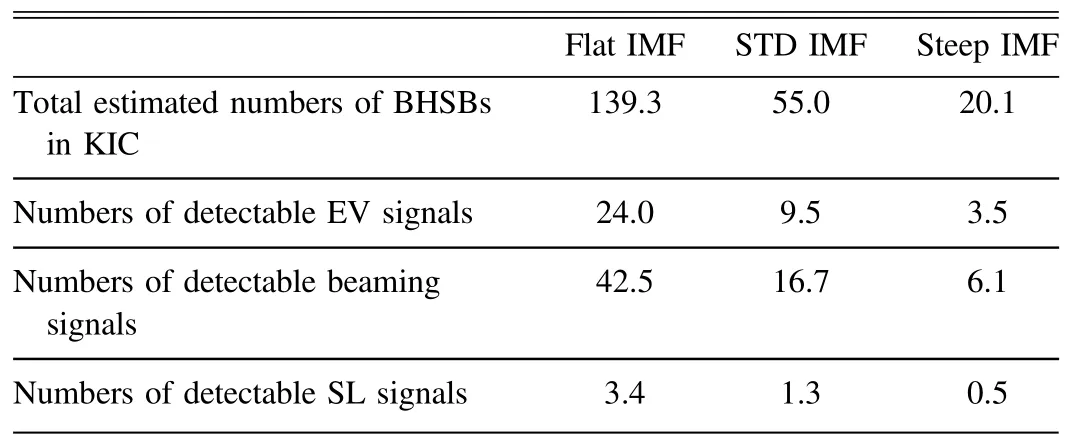
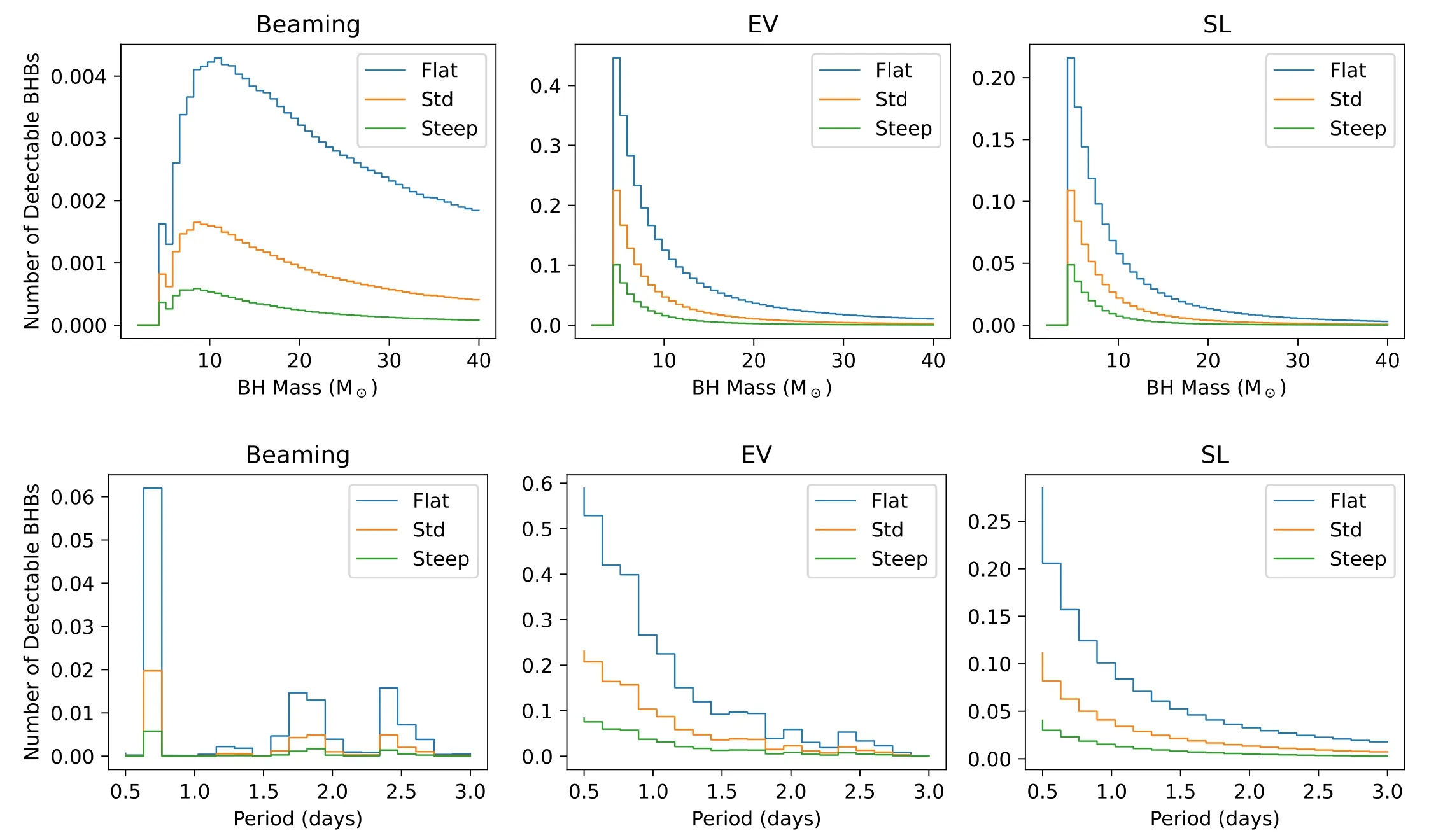
Figure 3.The searchable star number for the three kinds of signals (top-left: EV,top-right: beaming,bottom left: SL) against BH mass M• and orbital period P assuming that every star in KIC is in a BHSB with that particular combination of M•and P.The color bar indicates the logarithm of the searchable star number.The plot of EV signal shows that the signal changes fast along the period axis and slower in the BH mass axis.There are almost no searchable stars for EV signals with periods larger than 10 days.The searchable star distribution of the beaming signal is not smooth,which is mainly due to the change of the beaming signal is relatively slower,and its amplitude is similar to the spot noise level.These two reasons make the beaming signal detectability mainly depend on the spot noise level.The SL signal is larger with longer periods,but the detectability tends to be smaller.One reason is that the SL signal will vanish with orbital inclinationcos i

The EV signal is almost not detectable with an orbital period larger than 10 days while the beaming signal is almost not detectable in the region where the orbital period is shorter than 10 days and a BH mass smaller than 20M⊙.It is because the strength of the EV signal is inversely proportional to the square of the orbital period (sev∝P−2),and the amplitude of the beaming signal is only inversely proportional to the onethird power of the orbital period (sbeam∝P−1/3).This makes the EV signal larger than the beaming signal in the short period area and smaller than the beaming signal in the long period area while the spot noise is also with a higher strength in the short period area and is larger than the beaming signal with a small BH mass.The SL signal is stronger with long orbital period but lower detectable star numbers.The reason for this is the strict limitation on the inclination angle:cosi<⋆a.With the Kepler’s third law,longer orbital period will lead to a longer separation between the stars in a binary,which results in a smaller limitation for SL signal not to vanish.

3.3.Numbers of Detectable BHSBs

We first estimate the BH number distributionN•(M•)against BH mass,and then estimate the occurrence of massive binaries,i.e.,a binary contains a massive star,in field stars against the orbital period.Considering that not all massive binary can become a BHSB in the end due to binary interaction,we apply a coefficient αBIto mimic the BHSB occurrence against orbital period.By multiplying these two distributions together,we get the number distribution of BHSB,dNBH−star(dM•dP).

Following Masuda&Hotokezaka(2019)and Mashian&Loeb(2017),we assume that all stars with initial mass larger than 20M⊙will end up as a BH with mass above 5M⊙.So the number of the BHs above 5M⊙must correspond to the number of stars whose initial masses are all above 20M⊙,and the slope of two distributions must also be the same.From the IMF(Kroupa 2001),we then get the BH number distribution against BH mass:

whereIBH=CIMF,CIMFis a normalization factor following the rule above,and Γ is the IMF high end slope.The IMF itself is normalized so that the number of stars above 0.5M⊙calculated by IMF is the same with that in KIC.

To estimate the probability of a BH in a binary star,we start from its progenitor in stellar evolution,which is a massive binary.We follow the result of Sana et al.(2012),namely:

wherefbinmeans the occurrence of massive binaries,andCbinis a normalization factor according to Sana et al.(2012),which requires the possibility to be 0.5 through integrating the occurrence overP=0.1 day toP=103.5days.Thus we getCbin=0.057.

We also take account of binary interaction in the field binary model,which has not been considered by Masuda&Hotokezaka(2019).This partly corrects for an overestimate of the BHSB occurrence introduced by only regarding the massive binary model as the BHSB model.For estimation,we apply a coefficient αBI<1 to the occurrence of massive binary to represent the effect of binary interaction,which is from the result presented in Table 2 of Wiktorowicz et al.(2019).It means that a fraction of αBIout of all massive binaries will become BHSBs.Hence,the occurrence of BHSBs in the field is:

By combining the IMF of BH,dNBHdM•,and the BHSB occurrence,fBH-star,which we also follow from Masuda &Hotokezaka (2019),we get:

We assume that the probability distribution is not related to its companion stellar mass.Then the probability of a star with certain stellar mass having a BH companion is only related to the fraction of stars with that mass in the field,i.e.,the normalized IMF:

whereNtotis the total number of stars in KIC,and⋆dNis the number of stars in a certain mass bindM⋆.

Only BHSBs containing searchable stars can be detected.So we need to substitute the⋆dNwith the number of stars that can be searched,which is ΔN⋆.By integrating the probability above with the estimated number density of searchable stars ΔN⋆,we can get an estimate of detectable BH signal numbers

where the integral of stellar mass is converted into the summation of number density distribution of searchable stars in each stellar mass bin.

We apply three different IMF models all with the forms ofI⋆∝:the standard IMF model(Kroupa 2001),whose sl ope at high mass end is Γ=−2.3,the flat IMF model(Γ=−1.9,Schneider et al.2018) and the steep IMF model(Γ=−2.7,Kroupa &Weidner 2003).With the result in Table 2 of Wiktorowicz et al.(2019),we set αBI=0.028 for the standard IMF model,αBI=0.032 for the steep model and αBI=0.024 for the flat model.The IMF not only affects the star numbers,but also the total BH numbers,which is derived directly from the high mass end of the IMF.The flat IMF gives a higher estimate of BH number while the steep IMF does the opposite.

Two possible low mass cuts of BHs,3M⊙and 5M⊙,is also applied,respectively,in order to estimate the detectable number of mass gap BHs(i.e.,those BHs with mass between 3M⊙and 5M⊙).We assume that all stars with an initial mass higher than 18M⊙will become BHs with mass higher than 3M⊙,as we have done for 5M⊙.This treatment follows the result of Fryer et al.(2012),which indicates that the relationship between the mass of the star and that of its remnant is linear and the slope is approximately one.

4.Results

We calculate the number distribution of detectable signals of BHSBs with a BH mass upper limit of 40M⊙and orbital period upper limit of 100 days for all three types of signals.

By numerically integrating over the BH massM•and orbital periodP,we can obtain the total numbers of different signals.When the spot noise is not considered,the detectable numbers of signals with three different IMF models are shown in Table 1.The total numbers of BHSBs are shown as well.The result with different spot noise levels of low mass cut of 5M⊙are shown in Table 2.Here we show that the spot noise severely contaminates the EV and beaming BHSB signals,which reduced the number of detectable BHSB signals by more than 90%.

Table 1Total Number of Three Different Type of Signals Assuming Different IMF Models:Γflat=−1.9(Schneider et al.2018),Γnorm=−2.3(Kroupa 2001)and Γsteep=−2.7 (Kroupa &Weidner 2003)

Table 2Same as Table 1,but here Spot Noise has been Considered: Three Different Spot Noise Levels,i.e.,that of the Top 0.1%,1% and 10% Spot Noise Data,are used(McQuillan et al.2014)

The BHSBs number distributions versus BH mass and orbital period for the three signal types with all three IMF models and spot noise level of 10%are shown in Figure 4.It is clear that for all IMF models and different types of signals,most detectable BHSBs likely contain a low-mass BH with a short orbital period.This is a direct result of the BH IMF,i.e.,H(M•−5M⊙)IBH,which predominantly produces low-mass BHs,as well as the occurrence of massive binaries,which is inversely proportional to the orbital period.For the beaming signal the number of BHSBs is not the largest in the lowest mass bin.The trend of number distribution of the beaming signal in different period bins is not as clear as the other two signals.The reason is that the beaming signal is severely influenced by the spot noise,which is also shown in Figure 3.As in Equation (4),the beaming signal is smaller when BH mass is smaller.Besides,the beaming signal does change much with orbital period.So whether the beaming is detectable or not is mainly determined by the spot noise level.Although there are more BHSBs with smaller BH mass,the beaming signal is not significant enough to detect in most cases.Different IMF models show a large difference in total BHSB numbers.This implies that,the total number of the BHSBs to be found can be used to constrain the star evolution theory by comparing with our result.

Figure 4.The detectable BHSB number for different signals and different IMF models in each BH mass bin and orbital period bin.The upper panel shows the number distribution of BHSBs in different BH mass bins,while the lower panel shows the number distribution of BHSBs in different orbital period bins.The blue,orange and green step line is the detectable number of BHSBs in flat,standard and steep IMF models with spot noise level of 10%.The low mass cut for all three models are 5 M⊙.

In order to estimate the detectability of mass-gap BHs,a low mass cut for BHs at 3M⊙is applied.However,the number of detectable signals for all three signals in total does not change much with the lower mass cut.Although the total number of BHSBs increases with the lower mass cut,most of the BHSBs are still clustered in the zone with smaller BH mass,which makes the signal smaller thus less detectable.In the flat and STD model,the number of detectable BHSBs with a low mass cut of 3M⊙slightly increases than that with a low mass cut of 5M⊙while in the steep model,the number decreases.This can be explained that in the steep IMF model,there are more fractions of BHSBs with low BH mass than in the flat or standard(STD) model,which makes the signal strength smaller overall and less detectable.Although there is no significant increase in the number of detectable BHSBs,one still expects to find more BHs in the mass gap due to the BHs are clustered in the low mass zone.Recently,at least two mass-gap BH candidates have been found using photometry and RV measurements(Thompson et al.2019;Jayasinghe et al.2021),demonstrating a huge discovery space for massgap BHs.

The spot noise level has a significant impact on the detectability of sinusoidal-like phase curves produced by BHSBs,i.e.,EV and beaming signals.We plot the BHSBs number distribution versus BH mass and orbital period for the three signal types,standard IMF models,as well as spot noise levels at the (top) first,tenth,fiftieth,a hundredth percentile among all spot stars and the case where spot noise is absent,as shown in Figure 5.As expected,the number of BHSBs with detectable EV and beaming signals increase with smaller and smaller spot noise levels.

Figure 5.The detectable BHSB number distribution for all three types of signals with different spot noise level.The upper panel shows the number distribution of BHSBs in different BH mass bins,while the lower panel shows the number distribution of BHSBs in different orbital period bins.The same color step line is the detectable number of BHSBs with different spot noise level,which is the same between the upper and lower panels.The SL signal is not affected by the spot noise.

Looking at different signal types,when the spot noise level changes from 50% to 10%,the number of BHSBs with detectable beaming signal decreases more than that of EV signal.It is because the strength of beaming signal is less sensitive to both BH mass and orbital period than that of the EV signal.As shown in Section 2,sEV∝P−2andsbeam∝P−1/3.So the beaming signal level has a critical value,The critical value is around the spot noise level of 10%for the beaming signal.If the spot noise level is larger than this critical value,most of the beaming signal will be totally over-shone.On the other hand,with the increase of spot noise level,the number of BHSBs with detectable EV signal decreases smoothly.

To summarize,about one detectable signal for SL,and less than one detectable signal are expected for Doppler beaming and EV signal in KIC stars with the standard IMF model(Kroupa 2001).For flat IMF and steep IMF,this number would increase or decrease,respectively,as shown in Table 2,which is mainly due to the change in number of massive stars.The flat IMF model which predicts more massive stars generates more BHSB signals,while the steep model has less.The number of detectable SL signals is always larger than the other two signals,which is because the spot noise can only affect the detecting of phase curves,but not the SL signal,which is more likely a pulse.Although when the semimajor axis of orbit becomes larger,the magnification of SL signal increases while the requirement on the inclination angle also becomes more stringent (cosi<⋆a),SL signal still has a higher chance to be detected than the other two signals when the stellar activity is hard to distinguish.

5.Discussion

A previous study on searching for EV or beaming signals has been carried out with Kepler data(Faigler et al.2015).This search is an application of the BEER algorithm (Faigler &Mazeh 2011),which is to search for low-mass stellar companions with the combination of Beaming,Ellipsoidal and the Reflection/heating periodic modulations,having found several eclipsing white dwarf binaries.During the search,they first fitted the amplitude of the three signals,i.e.,EV,beaming and reflection.Then they make use of the ratio of the strength of the EV and beaming signals,which is only related to properties of the primary star under the assumption of lowmass companion,to check the likelihood by comparing the value derived from the prior distribution of the properties of the primary star and the value computed from the fitting result.However,this assumption does not hold in the case of a companion being a black hole,which may be one of the reason why this search did not find any BHSB or Neutron Star-Star Binary.Besides,according to the estimation in this work,the expectation of finding a BHSB in Kepler sample is not larger than 1 with EV and beaming signal.

5.1.Detailed Occurrence-period Relation

The relation between BHSB occurrence and orbital period isfbin∝p−β,i.e.,Equation (15);and β=1.0 is used above.According to Duchêne &Kraus (2013),the massive star binaries distributions can be divided into two,which contains a population of short period (≾Plog 1) binaries which contributes to about 30% of all massive binaries and a power law distribution β ∼0.5 in longer periods (Sana et al.2012).With the consideration of both the pile up in the former population and the uncertainty in the latter population,we apply β=1 in the computation.On the other hand,even with a long tail of β ∼0.5,it only contributes to a little in the number of detectable BHSBs.By applying β=0.5,which is mainly composed of longer period binaries,the total number of all detectable BHSBs will decrease by a factor of ≥10,as shown in Table 3.

Table 3The Change in Detectable BHSB Numbers with the Change in β from 1.0 to 0.5,where β is the Relation between the BHSB Occurrence and Orbital Period,i.e., f ∝p−β

When β is set to 0.5,the function becomes smoother,which means the number of BHSBs with short periods becomes smaller while keeping the same normalization in the two cases.In fact,with the upper limit of 300 days,the total occurrence is 0.36 forfbin∼P−1and 0.15 forfbin∼P−0.5,which is only half of the former.The amplitudes of EV and beaming signals drop with the increase of orbital period,thus these two signals are more sensitive to BHSBs with short orbital periods,as expected.As for SL signals,the limitation on the orbital inclination is more strict with longer orbital periods,which makes SL signal also more sensitive to BHSBs with short orbital periods.These two effects cause the number to become smaller when β=0.5,so the long tail of massive binary distribution does not contribute to the number of detectable BHSBs in a noticeable level.

5.2.Applications to other Photometric Data

Our work only contains one unique data of Kepler,the KIC(Mathur et al.2017),containing the stellar mass and distance and many other parameters of well observed stars whose light curves are cataloged.If the statistical properties of stars,as well as their distances,observed by an instrument are similar to KIC stars,this work can also be applied to photometric data taken by that instrument.By considering the number of well observed stars (or those whose light curves are cataloged),we can roughly calculate the numbers of detectable BHSB signals.

Our analysis shows that,out of 200,038 KIC stars with good quality light curves,about 1 BHSBs could be found.One expects that the increase of telescopes and improvement of the data quality,the number of BHSBs would also grow.Currently operating and planned transit telescopes include TESS (Ricker et al.2015),PLATO (Rauer et al.2014) and Earth 2.0 (Ge et al.2022),hosted by Shanghai Astronomical Observatory,Chinese Academy of Sciences.There is a lot in common between planet searching and BH photometric searching,so these telescope mentioned above may have a possibility to find new BH candidates as estimated.

5.3.Caveats of the Current Estimates

One issue in our work is that the BHSB model we used is probably over-simplified,i.e.,it simply assume that the binary interaction including merger and kick will only affect the total number of the BHSBs and does not affect the shape of the distribution.The BHSB fraction in reality is also not well constrained,since there are only less than 100 BHSBs(candidates) recorded (Tetarenko et al.2016).The BHSB formation process also contains lots of uncertainty.

Another issue in our work is that the noise level of many stars (characterized by their 15 hr CDPP values) can be much higher than Equation(10),decreasing the S/N of any potential BHSBs.On the other hand,as the baseline that can be used is 4 yr,rather than 15 hr,S/Ns of periodic signals (which we calculate simply by dividing the signal amplitude by the amplitude of the CDPP) like the ones considered in this work will be boosted.The real impacts of these two effects will involve a detailed simulation of light curves and instrumental response which is beyond the scope of this work.

6.Summary

Photometric signals from survey data have been used to find BHSB candidates,e.g.,Thompson et al.(2019) and Jayasinghe et al.(2021),as well as to detect periodicity from known pulsar binaries,e.g.,Pal et al.(2020).These studies show the potential of high-precision photometry to find BHSBs,including mass-gap BHs,and other compact objects in binaries.In this work,we estimate the number of detectable BHSB signals from the KIC.We first calculate the maximum searchable distance and count the number of searchable stars within that distance.We then estimate the effect of stellar activity on the searchable star number of sinuous signals as well.The BHSB number among these stars is estimated with a field binary model and the result of binary interaction simulation(Wiktorowicz et al.2019).

If we take the STD IMF model with a low mass cut of 5M⊙and a spot noise ratio of 1%,there will be 0.2 detectable EV signals,0.4 beaming signals and 1.4 SL signals.Note that these signals could come from the same systems.The result indicates that the number of the flat IMF model is about 3 times of that with the STD model and more than 5 times of that in the steep IMF model.The change in numbers of BHSBs of different spot noise level is much stronger than the change in numbers of BHSBs of different IMF models,especially in EV signals.As stated in Section 3,the phase and period of the spot noise is not stable in the timescale of the spot noise lifetime.With the increase of observation time,the influence of spot noise on the signal amplitude will be reduced,and the number of detectable BHSBs will increase.Mass-gap BHs can also be found,and due to the limitation from BH IMF,we predict that about half of the detectable BHSBs will include BHs with masses below 5M⊙.

Since the possibility of a star having a BH companion is so small,the only thing one can do is to observe more stars with higher accuracy.One expects that this number will increase as more and more photometry telescopes of higher precision will be launched in the future.For example,the telescope Earth 2.0,also known as ET (Ge et al.2022),as mentioned above,has a larger field of view (500 square degrees planned),and can finally record up to 1,200,000 high quality light curves,which is 6 times as much as the number of Kepler.With this telescope,we expect to find about 10 BHSBs including BHs above 5M⊙with these types of signal in a STD IMF model.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (NSFC) grants 12073091 and 12273122,Guangdong Major Project of Basic and Applied Basic Research Grant (2019B030302001),and a science research grant from the China Manned Space Project (CMS-CSST-2021-B11).