基于ANSYS橡胶圆筒与刚体的大变形接触分析★

邓 苗

(中铁十五局集团第二工程有限公司,上海 201700)

0 引言

随着社会生产工业化程度的逐步提高,橡胶圆筒以耐腐蚀、耐热、耐老化和耐氧化等特点在建筑、电力和机械等领域广泛使用。但是随着橡胶圆筒使用频率和时间的增长,与刚性体接触引起的磨损和结构失效屡见不鲜,严重的甚至导致建筑与机械结构损坏和安全事故。因此,橡胶圆筒与刚性体之间的接触分析十分重要,它可以为增强橡胶圆筒寿命、提高结构的耐久性和安全效率提供一定参考。

国内外专家学者对橡胶圆筒与刚性体的大变形接触分析展开了一系列研究。在橡胶圆筒接触分析方面,杨开云等[1]用完全拉格朗日方程和增量求解方法对橡胶材料的大应变接触进行非线性分析,提出间隙元法分析接触问题并获得橡胶圆筒大应变位移反力曲线。王伟[2]和Chiara等[3]基于非线性有限元方法考察橡胶材料不可压缩性和大变形引起的几何非线性与接触非线性,研究橡胶圆筒在沟槽内的接触变形和密封界面上的接触应力分布规律,并分析同轴度对橡胶圆筒力学性能的影响。Jan[4]和桑建兵等[5]通过橡胶圆筒的非线性有限元计算分析不同介质压力对橡胶圆筒力学性能的影响,并获得橡胶圆筒的应力分布规律、主接触面以及侧接触面接触应力的分布曲线。Saeed[6]、王朋波[7]和Takuya等[8]将可行方向内点法引入橡胶圆筒大变形接触问题的有限元分析中,将超弹性体接触问题描述为不等式约束下的最小化问题并导出相对应的KKT最优化条件。上述分析对橡胶圆筒的接触位移和应力分布等力学性能进行全面分析,而未考虑尺寸效应和摩擦程度对结构接触性能的影响。

针对软物质及接触问题,孙晓昊[9]和Gao等[10]对橡胶等软物质大变形、接触和黏附等非线性力学行为进行理论与有限元模拟研究并提出处理复杂非线性行为的有限元方法,解决了软物质大变形和复杂边界条件下的接触问题。吴庆勇[11]考虑两级伸缩支腿间以及与底座结构间的接触和摩擦等非线性因素,通过有限元计算获得伸缩支腿的刚度、应力分布和接触情况,为结构优化提供依据。刘波等[12]应用大变形理论对刚性锥压缩作用下橡胶类材料半空间锥尖附近的应力奇异场进行了分析。上述分析主要考察软物质材料的接触力学性能并优化研究接触问题的有限元方法,而对接触性能的影响因素缺乏讨论。

上述研究对于橡胶圆筒与刚体的大变形接触的尺寸效应和摩擦程度的影响研究十分有限。基于此,本文基于ANSYS19.2展开橡胶圆筒与刚体的大应变接触分析,讨论橡胶圆筒与刚体大应变接触的接触求解方程、材料特性和建立有限元模型等数值原理,考察橡胶圆筒摩擦系数和尺寸效应对结构接触力学性能的影响,提出接触最大应力和最小应力随摩擦系数和厚度变化的拟合公式,并根据应力应变结果明确橡胶圆筒与刚体接触过程中的最不利位置。

1 有限元原理

1.1 接触求解

本文采用接触表面法求解接触问题。接触表面法是将两个相互接触的物体,分别定义为主动和被动接触体,同时将已接触或可能接触的区域设置为接触表面。在数值计算中仅考虑主动接触面的点与被动接触面中线和面接触问题,最后将接触力位能叠加到总系统的能量泛函中并导出接触问题的数值方程。另外,多个接触物体可转化为两两接触的物体考虑。导出的有限元方程如下:

tKL+tKNLuk=t+ΔtP-tQ。

其中,tKL为t时刻线性总体刚度阵;tKNL为t时刻非线性影响刚度阵;uk为节点位移增加量;t+ΔtP为t+Δt时刻外荷载列阵;tQ为t时刻物体内原有的应力tS引起的等效节点力阵。

1.2 材料特性

由于橡胶类等大变形材料非线性特征十分明显,其应力应变关系通常采用应变能函数来描述,在数值分析中橡胶材料被视为各向同性超弹性材料,其应变能函数表达式为:

W=W(I1,I2,I3)。

其中,I1,I2和I3为Cauchy应变张量的3个不变量,具体表达式如下:

其中,B=FFT为左Cauchy应变张量;F为变形梯度张量;λi为主延伸率。

由此可得第二类Piola-Kirchhoff应力张量:

其中,E为Green-Lagrange张量。对不可压缩橡胶类材料I3=1,则Cauchy应力张量为:

则Cauchy应力表达式转化为:

由上式可得到Cauchy应力的表达式:

1.3 有限元模型

本文基于某建筑结构中橡胶圆筒与刚体接触实例进行分析,具体结构参数为:橡胶圆筒内外半径分别为50 mm和100 mm,圆筒上下为刚性体,其长度200 mm。本实例采用Plane182单元模拟橡胶。橡胶圆筒的材料为二参数的Mooney模型,其中C10=2.5 MPa,C01=1.1 MPa,D=0.000 001 33,弹性模量为6.9 GPa,泊松比为0.499 67。加载及边界条件:下侧刚性体固定,上侧刚性体向下移动12.5 mm。结构有限元模型和接触分析流程分别如图1,图2所示。

2 摩擦系数的影响

橡胶圆筒与刚体接触的粗糙程度是影响接触力学性能的重要影响因素之一。本文考察了不同摩擦系数对结构接触力学性能的影响,选取了0.12,0.24,0.36,0.48,0.60,0.72,0.84和0.96等8个不同摩擦系数考察接触粗糙程度对结构应力应变分布规律的影响。图3和图4分别为0.12,0.36,0.60和0.84四个典型摩擦系数下的结构位移云图和应力云图,由图3可知,在压缩过程中橡胶圆筒的上下左右内侧压力均为正值且在4个区域出现最大值。从图4可以看出,正摩擦应力始终分布在橡胶圆筒的上侧和下侧。

表1为不同摩擦系数下结构最大位移与最值应力,分析可知,粗糙程度不影响结构的最大位移,不同摩擦系数下的最大位移均为12.5 mm,结构的最大应力和最小应力均随摩擦系数的增加而减小,最大应力在摩擦系数0.12处的2.85 MPa。通过图5可以看出最小应力和最大应力随摩擦系数逐渐递减,采用多次项函数进行拟合,拟合的具体表达式分别为f=6.57-3.03μ+1.63μ2(×104)和f=2.87-0.19μ+0.10μ2(×106)。

表1 不同摩擦系数下结构位移与应力

3 厚度的影响

尺寸效应已成为影响橡胶圆筒与刚性体接触力学性能的重要因素之一。本文通过选取20 mm,30 mm,40 mm,50 mm,60 mm,70 mm和80 mm等7个圆筒厚度下接触性能的变化规律考察结构尺寸对橡胶圆筒与刚性体接触力学性能影响程度。如图6所示为20 mm,40 mm,50 mm和60 mm四个典型厚度下的结构位移云图和应力云图,由图6可知,在t=20 mm时,橡胶圆筒在压缩过程中上下左右内侧压力分布较为均匀且在上下两侧出现最大值。在t=40 mm时,压力分布相对均匀,较大压力主要集中在上下两侧且内侧大于外侧。在t=60 mm和t=80 mm时,压力分布分别集中在右上侧和上侧且最大值分别发生在中间厚度处和外上侧。可以发现,厚度越大压力分布越向施加荷载处集中。图7为不同厚度下的结构接触应力云图,分析可知,正摩擦应力始终分布在橡胶圆筒的下侧且随厚度增加而增加。

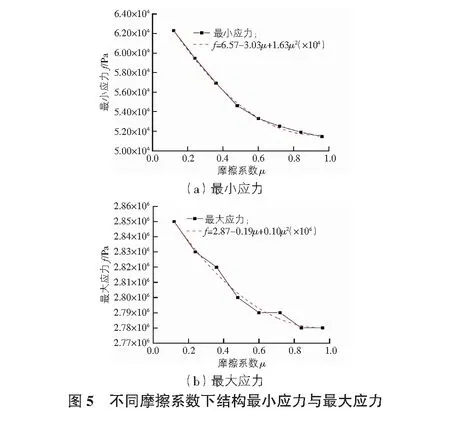
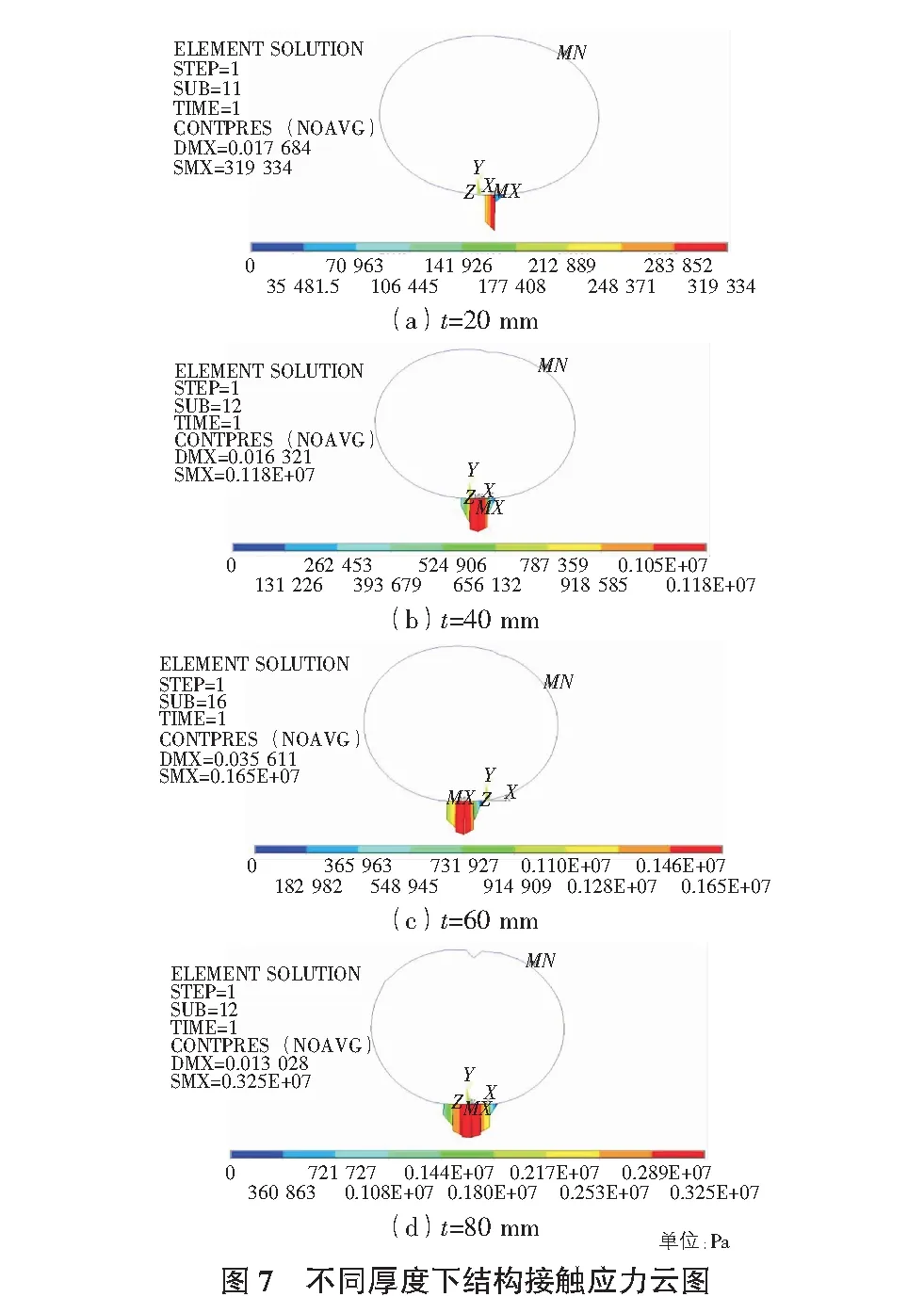
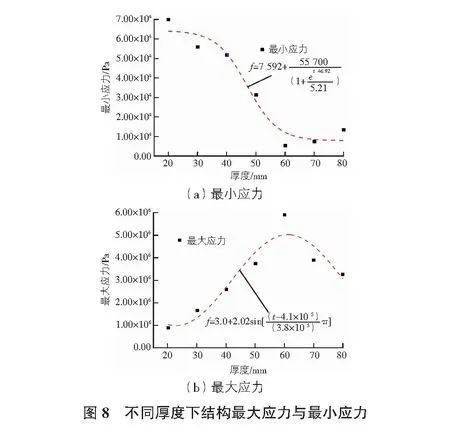
表2为不同厚度下结构最大接触位移与应力,分析可知,结构位移随着厚度增加先增后减,在t=60 mm达到最大值56.4 mm。结构的最小应力随厚度增加先减小再增加,在t=20 mm达到最大值68 840 Pa,最大应力随厚度增加先增加再减小,在t=60 mm达到最大值5.89 MPa。图8为最小应力和最大应力随厚度变化的非线性拟合曲线,具体表达式分别见式(1)和式(2)。

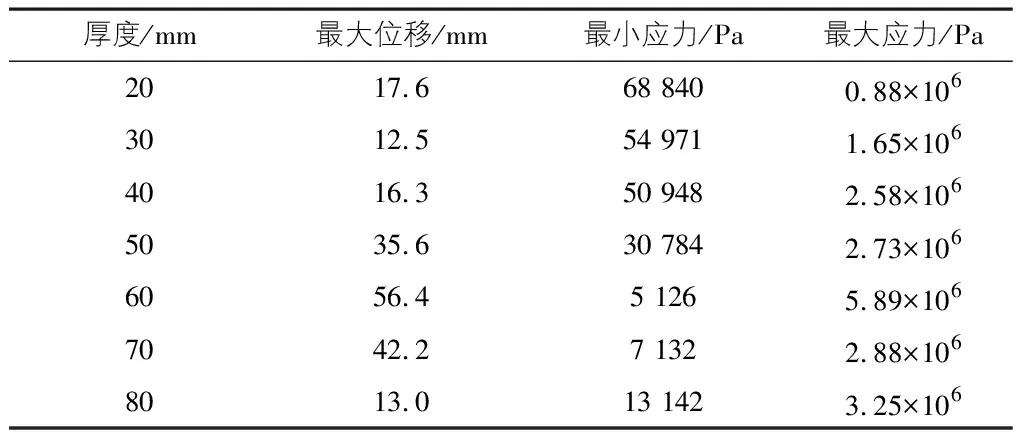
表2 不同厚度下结构最大接触位移与应力

(1)

(2)

4 结论

本文基于ANSYS19.2对橡胶圆筒与刚性体的大变形接触进行有限元分析,阐述橡胶圆筒与刚体大应变接触分析的有限元原理,考察橡胶圆筒摩擦系数和尺寸效应对结构接触力学性能的影响,获得以下结论:

1)在不同摩擦系数的压缩过程中橡胶圆筒的上下左右内侧压力均为正值且在4个区域出现最大值,正摩擦应力始终分布在橡胶圆筒的上侧和下侧。

2)粗糙程度不影响结构的最大接触位移,结构的最大应力和最小应力均随摩擦系数的增加而减小,最大应力在摩擦系数0.12处的2.85 MPa。

3)橡胶圆筒厚度越大压力分布越向施加荷载处集中,正摩擦应力始终分布在橡胶圆筒的下侧且随厚度增加而增加。

4)圆筒接触位移随着厚度增加先增后减,结构最大接触应力随厚度增加先增加再减小,在t=60 mm达到最大值5.89 MPa。