电动汽车充电路径规划研究*

赵文清 王继发

（华北电力大学计算机系 保定 071003）

1 引言

电动汽车的动力采用对电动车充电，放置充放电电瓶作为存放电动汽车驱动动力的承载装置，但是电瓶对电动汽车所能承担的动力有限。因此，对于电动汽车充电问题便成为当今社会致力于研究该内容的专家学者的“重头戏”，在满足电动汽车日常充电的需求的基础上，还需对充电路径进行深入研究并给予优化，以此保证日渐增多的电动汽车在最有效的时间内完成对车辆的充电。

电动汽车充电路径规划可以从多个角度进行分析。文献［1～2］考虑交通网络和配电网络等路径引导制约因素，将交通路况信息阻碍和充电桩电力调度作为研究目标，达到路径规划目的。文献［3］把动态路径规划问题分割成初始阶段路径选择和充电桩资源抢夺，把多目标路径规划的时间离散化处理，佐以资源智能预警，实现动态网络规划。文献［4～7］将路径规划算法作为主要研究对象，通过优化算法提高多目标路径的收敛与搜索能力。文献［8］针对非满载问题进行研究，探索最优解的性质，分析总结了较紧的上下界，以及路径规划过程的最坏情况与解决方案。

本文通过对交通网络、配电网络、车辆本身的各项属性进行分析，定量的设置电动汽车在路径规划过程采用智能水滴算法所涉及到的速度、泥土量等数据，利用智能水滴算法的数学模型，采用libsvm 对所选数据列表进行预测分析，获取交叉验证精度，确定最佳路径，实现智能水滴算法在电动汽车充电路径规划上的应用。

2 智能水滴算法模型构建

2.1 智能水滴及其算法

智能水滴算法是根据自然界水滴汇集成流，然后流入大海的过程中“自由选择”流经路径的现象仿真得到的，Shah-Hosseini 根据水滴的这些属性，将之命名为智能水滴（IWD），从而演化出智能水滴算法［9］。根据水滴的特性可以构建出抽象的数学模型，这种模型的属性主要是包含水滴中携带的泥土量soil 和水滴在不断更新泥土量的同时不断变化的速度velocity。文献［10～12］描述了智能水滴算法的实现原理及其合理性，文献［13～14］建立模型验证了其性能的优势，文献［15～16］分析算法的局限性，优化智能水滴的寻优方式，提高算法的搜索能力。文献［17～19］采用不同算法与智能水滴算法混合，使用改进的智能水滴算法在车场分配和路径搜索选择上展开研究。

2.2 智能水滴算法数学模型

智能水滴所拥有的两个重要属性是水滴经过路径所含泥土量和水滴的当前速率。但是由于水的流动特性，导致这两个属性都是处于变化状态的，因此，智能水滴算法的目的是按照某些约束力，从某个节点到下一个节点找到水滴前进的最佳的一条路径。

通过数学定量分析对智能水滴算法进行定量分析。假设水滴的当前位置为i，此时的速度为velocity（i），下一节点的位置为j，j位置的速度为velocity（j），由速度与从i 到j 的泥土量soil（i，j）成非线性反比关系可知表达式为

其中，as、bs、cs为用户预先设定的静态参数。

在水滴位置的变化过程中，水滴的含沙量的变化量和路径中的变化量是相等的，泥土量的变化量和水滴移动所需的时间呈现非线性反比关系：

其中，as、bs、cs为可设定的模拟参数。time(i，j)为时间函数。

当水滴在两节点间移动过程中，水滴中的含沙量和路径中河道的泥土量在实时变化时的公式更新可以表示为

其中，ρn∈(0，1)，权重系数，一般取值0.9。

水滴的位置在时刻变化，在水滴到达下一节点前，会有多项泥土量的阻碍，也会形成多条路径的选择，水滴为了更快、更容易到达下一节点，会选择一条最佳路径进行前进，在这条路径中，水滴在行进时的含沙量最少，速度最大。按照智能水滴在两节点间位置移动，假设路径概率为(j)，表达式为

其中，soil(i，j)两个节点间的泥土量；VC(IWD)为智能水滴节点集合；f(soil(i，j))的表达式如下：

其中，ε为极小的正数，其作用是保证函数f的分母不为零。函数g 是i，j 两个位置之间泥土量的修正函数，表达式如下：

其中，函数min 表示当前节点未流过的所有路径的泥土量的最小值。

为实现寻找水滴流入大海的最优路径，可以在智能水滴算法的的数学模型的基础上进行模拟水滴选择路径的流程。将拟定解决的问题数据集作为输入信息，得到的优化解为输出信息。采用迭代的方式对数据集的迭代，当迭代次数不够或者是精度没有满足，随机选择当前节点，然后根据数学条件选择下一节点，选择的依据是水滴的含沙量和河床中所含泥土量。

3 基于IWD算法的路径规划

3.1 智能水滴算法设计

路径规划需要考虑电动汽车在行驶过程中可能出现的各种阻碍。在本文中，将可能出现在道路规划中的交通网络、配电网络、电动汽车本身阻碍看作智能水滴算法的泥土量，在泥土量不同的情况下，选择路径的概率也会不同，根据路径情况，选择路径概率大的最为最优路径。根据最优路径，产生最优规划方案。

3.2 智能水滴算法模拟实现

上一节中提到将交通网络、配电网络、车辆本身所产生的对充电路径造成阻碍的一些因素看作智能水滴的泥土量，将不同类型的泥土量进行量化模拟。在泥土量设置中，设置了51 项泥土量，在大数据的模拟环境能够更好地展现智能水滴算法的特点。根据模拟的泥土量数据，在智能水滴的两个属性的基础上，对数据进行处理，从而实现路径选择的目的。

根据智能水滴算法，声明路径中的泥土量pathsoil 并对其进行初始化，将路径中的泥土量设置初始值为1000。将智能水滴分代迭代，设置为30代，每代执行以下操作。

创建IWD，对IWD 进行迭代，随机选择设定泥土量的行数，在选择的行数长度中计算pathsoil 范围内的一部分，然后更新IWD 访问列表，查找IWD从i 到j 的概率，其中j 不在访问路径列表中。将每一代的IWD 数据分为10 个子集，把每个IWD 从当前位置移动到下一位置，直到把自己全部遍历。一个子集的开始，根据智能水滴算法的数学模型，在路径泥土量pathsoil 矩阵范围内计算g(soil(i，j))、智能水滴f(soil(i，k))集合元素之和，找到最小泥土量（minsoil(i，j)）。此时检查i 是否在访问列表当中，根据式（7）计算泥土量，并计算下一个数据，信息增益排序滤波器对输入的数据采用搜索排序，对602条数据的51个属性进行排序，标准化概率。

根据排序数组标准化排序，获取新特征排序，然后更新IWD。首先获取IWD 的初始速度和位置，在验证中，设置水滴的初始速度velocity为100，含沙量soilcontent 为0，然后计算速度，按照式（1）进行更新，设置av=1，cv=1，bv=0.01；计算泥土量，根据式（3）对泥土量进行更新，设置as=1，bs=1，cs=0.01，ρ=0.9。

基于选定的位置创建简化数据集，利用Matlab运行libsvm，根据svmtrain创建动态数据预测结果，获取交叉验证精度。然后进行下一代的迭代，经历30 代的迭代，更新最佳路径，选择最大概率的IWD，更新每条路径的泥土量soil(i，j)，根据访问列表中的特征将全局最佳路径写入文件，输出最佳路径作为智能水滴的最佳路径。

4 路径规划模型分析

4.1 函数验证

智能水滴算法是利用智能水滴速度和泥土量这两个属性，加之本身具有的灵活性，对路径进行优化。在对智能水滴算法的验证中，使用四种测试函数对智能水滴进行验证，通过函数本身与设定值之间的图像展示，可以直观地看出算法的有效性。

4.1.1 Rosenbrock函数验证

函数表达式为f(x1，x2)=-10 ≤x1，x2≤10。该函数使用的是二维函数，设置全局的最小值f(1，1)=0。Rosenbrock 函数立体图见图1。根据立体图可以看出二维Rosenbrock函数在最低点取得全局最小值，可以测试求解方法的执行能力。该函数的仿真实验函数值收敛曲线见图2，通过图线的曲线走势，可以找到最优值。

图1 Rosenbrock函数立体图

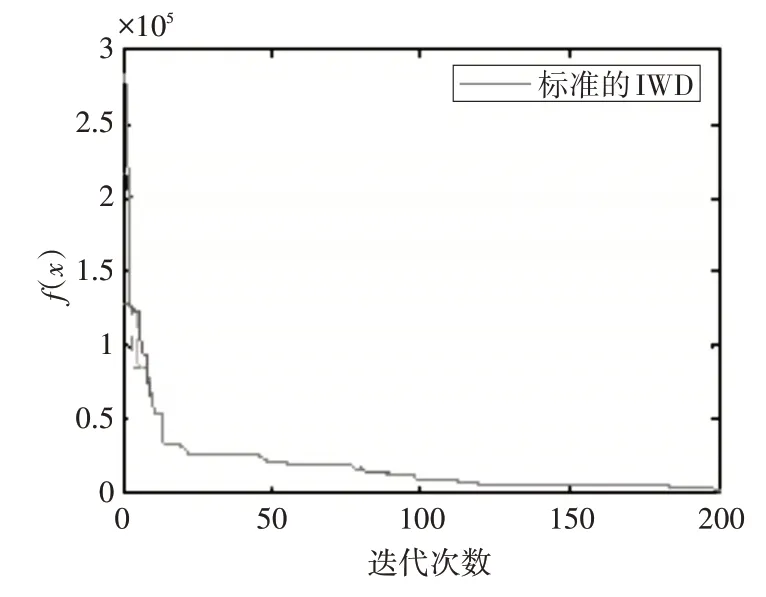
图2 Rosenbrock函数仿真实验函数值收敛曲线

4.1.2 Beale函数验证

函数表达式为f(x)=(1.5-x1+x1x2)2+(2.25-，-4.5 ≤x1，x2≤4.5 。该函数使用的是二维函数，设置全局的最小值为X*=(3，0.5)，f(X)*=0。二维Beale函数的立体图见图3。根据立体图可以看出二维Beale 函数是多峰函数，多峰函数可以测试全局最优和局部最优的搜索能力。

图3 二维Beale函数的立体图

4.1.3 Rastrigin函数验证

函数表达式为f(x)=cos(2πx2))+20 ，-5.12 ≤x1，x2≤5.12 。该函数使用的是二维函数，设置全局的最小值为f(0)=0。二维Rastrigin 函数的立体图见图4，根据立体图可以看出二维Rastrigin函数是多峰函数，多峰函数可以测试函数的局部极值。该函数的仿真实验函数值收敛曲线见图5。

图4 二维Rastrigin函数的立体图

图5 二维Rastrigin函数仿真实验函数值收敛曲线

4.1.4 Griewank函数验证

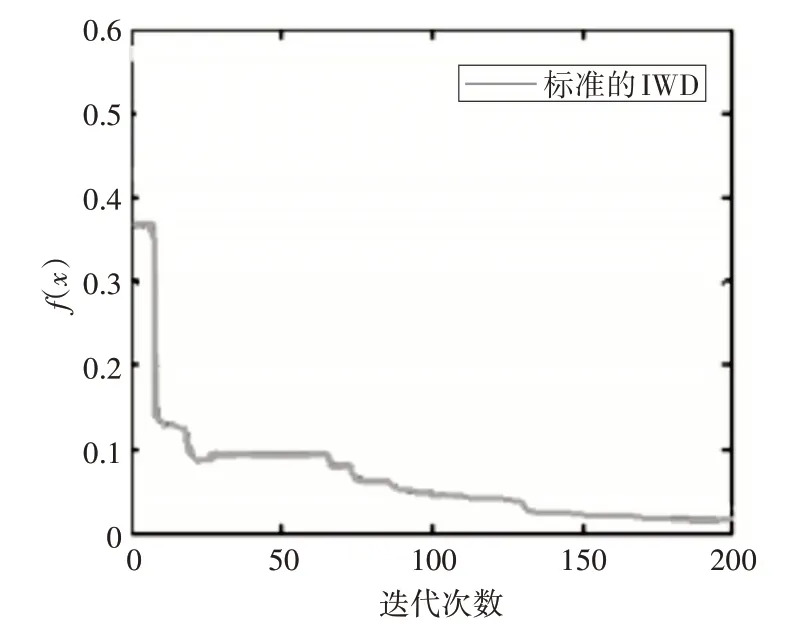
图6 二维Griewank仿真实验函数值收敛曲线

4.2 数据迭代最优值

智能水滴算法在上述测试函数的测试中，通过立体图和曲线观察发现，智能水滴算法是可以实现算法的有效性的，根据测试函数的函数表达式和原有设定的值，求解出数据算法的最优值和迭代的次数，见表1。通过数据可以直观地看出智能水滴算法的迭代情况。

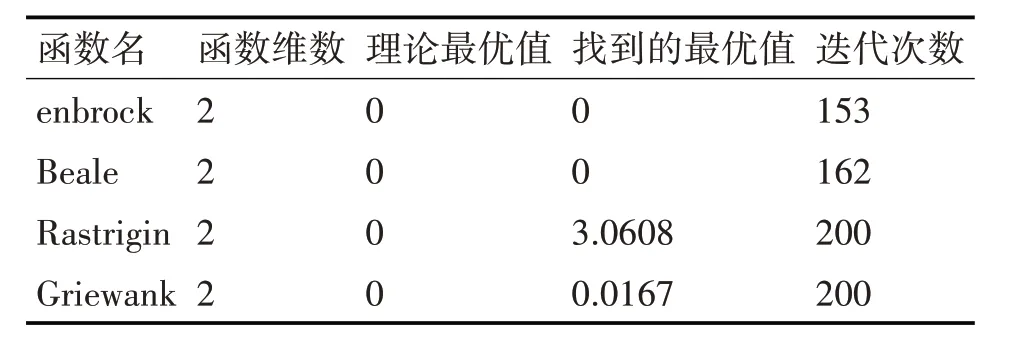
表1 四种函数验证智能水滴算法找到的最优值和迭代次数

通过表1 可见，二维Rosenbrock 函数在迭代153 次达到最优值，二维Beale函数在迭代162 次达到最优值，二维Rastrigin函数和二维Griewank 函数在迭代200 次基本趋于理论最优值。从数据值看，智能水滴算法在有限的迭代次数后达到最优值。

5 结语

研究基本实现了智能水滴与电动汽车充电路径的结合，从数据结果可以看出，智能水滴算法在电动汽车充电路径规划上是可行的。智能水滴算法的运用是一个很便利、能够动态掌握电动汽车的充电路径规划，但是有些方面的不适用是需要改进的。后期，将主要针对智能水滴算法的改进进行研究，并研究数据挖掘以及大数据分析对人类生活的便利程度。