贝叶斯神经网络方法对原子核β衰变寿命的研究

李伟峰 张晓燕 牛中明

（安徽大学 物理与光电工程学院 合肥 230601）

宇宙重元素起源是原子核物理与核天体物理共同关注的热点课题［1-2］。快中子俘获过程（r-过程）通过连续的中子俘获和β衰变合成了约一半比铁重的元素。β衰变是r-过程中的关键过程，其中β衰变寿命决定着r-过程的时间标度，也是近年来r-过程研究的热点［3-4］。虽然近年来对β衰变寿命的测量取得了很大进展［5-6］，但在r-过程路径上的许多核的衰变寿命仍然无法测量，特别是对于N=126附近的原子核。因此，对β 衰变寿命的理论预测具有重要意义。研究原子核β 衰变寿命的理论模型主要包括唯像公式［7-8］、Gross 理论（GT）［9-12］，准粒子无规相位近似（Quasiparticle Random Phase Approximation，QRPA）方法［13-18］和壳模型［19-22］等。壳模型可以成功地应用于描述轻核或幻数附近原子核的β衰变寿命，然而，由于组态空间过大，壳模型无法用于研究远离幻数的中重质量原子核。唯像公式、Gross理论和QRPA方法可用于描述核素图中大多数原子核的β衰变寿命，然而，其对β 衰变寿命的预测精度仍不能达到r-过程研究的需要。当外推至未知核区，各个理论的预言结果仍然存在较大偏差，尤其是N≳ 126的重核区［23］。然而，由于强相互作用与核多体计算的复杂性［24-25］，使得原子核β衰变寿命的精确理论预测相当困难。因此，对原子核β 衰变寿命的精确预测仍然是原子核物理中一个重要但尚待解决的问题。

近年来，机器学习在很多方面取得了令人瞩目的成就，是当前科学技术领域最为热门、发展最快的方向之一［26］。机器学习与物理学的结合是近年来新兴的交叉前沿领域，引起了广泛关注，已被用于粒子物理［27-29］、凝聚态物理［30-31］和天体物理［32-33］等领域。它为物理研究提供了一个强大的工具，在提取复杂非线性系统的相关特征方面功能强大，可以用来解决一些传统方法难以解决或暂时无法解决的复杂物理问题。在原子核物理中，机器学习方法也被广泛用于研究各种原子核的性质，如原子核的质量［34-35］、电荷半径［36-37］、α衰变［38-39］、原子核低激发谱［40-41］以及原子核的β 衰变寿命［42-43］等。贝叶斯神经网络（Bayesian Neural Network，BNN）方法通过引入先验可以自动地避免过拟合，并且可以量化模型预言的不确定性，因此也成为研究原子核性质的重要工具之一。近年来，BNN已被成功用于研究原子核的质量［44-48］、电荷半径［49］和原子核的低激发谱［50］以及原子核的裂变产额［51］等。相比传统的原子核理论模型，这些机器学习方法一般可以取得更高的预测精度。

基于BNN 方法，文献［52］通过学习β 衰变实验寿命与理论模型寿命的对数差，获得当时寿命预测的最高精度，对于寿命小于1 s 的原子核，其精度约为0.2 个数量级，即在约1.6 倍的范围内再现实验数据。与文献［52］不同，本论文将使用贝叶斯神经网络方法直接学习原子核的β 衰变寿命，验证机器学习直接预测β 衰变寿命的精度，并通过与实验数据以及其他核模型的结果进行对比，分析BNN方法的预言能力，为采用BNN方法直接学习原子核性质提供参考。

1 理论模型

在贝叶斯方法中，模型参数ω使用概率分布描述。首先，根据先前经验，引入先验分布p（ω）来描述ω的可能取值。假设已知实验数据集D=｛（x1，t1），（x2，t2），…，（xN，tN）｝，根据贝叶斯定理对先验分布p（ω）进行更新，即：

式中：xn，tn（n=1，2，3，…，N）分别是输入和输出数据，N为实验数据的数量；p（D|ω）是似然函数，它包含了由观测结果得到的参数ω的信息；p（ω|D）是已知数据D后参数ω的概率分布，称为后验分布；p（D）是实验数据的分布，其作为归一化的常量，保证了后验分布是一个全空间积分为1的有效概率密度。

似然函数p（D|ω）通常取高斯分布，即p(D|ω) =e-χ2/2，其中函数χ2表示为：

这里标准差参数Δtn是与第n个数据相关的噪音误差，与文献［44］类似，其平方的倒数被设置为伽马分布。指定p（ω）和p（D|ω）后，本文使用马尔科夫链蒙特卡罗方法对后验分布p（ω|D）进行采样。在BNN方法中，函数y（x，ω）用神经网络来描述，对于单隐藏层神经网络，其表示形式为：

式中：x= ｛xi｝；ω= ｛a，bj，cj，dji｝；H是隐藏层神经元的个数；I是输入量的个数。该神经网络的总参数量为（2+I）×H+1。由于模型参数被描述为概率分布，BNN 方法使用函数y(x，ω)的数学期望〈y 〉及其标准差作为其预测值和误差。

由于本文涉及的原子核β衰变寿命横跨约十个数量级，因此，使用寿命对数lg（T1/2）的均方根（Root Mean Square，RMS）偏差来评估核模型的准确性：

文献［52］发现，在神经网络的输入层中引入衰变能和与对效应相关的物理量，通过学习β 衰变寿命实验数据和理论预测的对数差，可以显著提高神经网络预言β 衰变寿命的准确度。因此，本文也将在神经网络中引入这两项，研究它们在直接学习原子核β 衰变寿命的神经网络中的作用。为此，本文采用以下三种网络结构，它们的输入变量、隐藏层神经元个数、激活函数和输出变量如表1所示。其中：Z和N是原子核的质子数和中子数；Qβ为β衰变的衰变能，取自Weizsäcker-Skyrme（WS4）模型［53］；δ=((- 1)Z+(- 1)N)/2，用于区分偶偶核、奇奇核和奇A核。不同神经网络选取相应的隐藏层神经元个数，以保证各神经网络的总参数量一致。三种网络的输出均选为lg（T1/2）。用于训练神经网络的实验数据取自NUBASE2020［5］，本文只保留Z、N≥8、Qβ>0且T1/2<106s的实验数据，共计1 051个。该数据集被随机分为训练集和验证集，训练集占总数据集的80%，即840 个，余下的211 个作为验证集。为了检验结果的稳定性，以BNN-I4 为例，通过多次随机划分训练集和验证集，发现BNN计算结果与训练集和验证集中实验数据的均方根偏差σRMS（lgT1/2）的变化均为10%左右。

表1 各神经网络输入变量、隐藏层神经元个数、激活函数和输出变量Table 1 Input variables, number of hidden layer neurons, activation functions, and output variables of various neural networks

2 结果与讨论

为了评估BNN 方法预测核β 衰变寿命的全局可靠性，三种神经网络方法的预测结果相对于实验数据的均方根偏差σRMS（lgT1/2）如图1 所示。图中分别给出了寿命T1/2<106s、T1/2<103s 和T1/2<1 s 的结果。相较于BNN-I2方法，BNN-I3和BNN-I4方法在神经网络的输入层引入更多相关的物理量，可以显著提升神经网络方法对衰变寿命的预言精度。尽管BNN-I3方法与BNN-I4方法对T1/2>103s以上训练集原子核预言精度几乎一致，但在验证集中，BNN-I4与实验值的结果更为符合。由此可见，在神经网络输入层中引入物理量δ，可以提高神经网络对β衰变寿命的预言能力。本文BNN-I4 方法得到训练集和验证集的精度分别为0.39 和0.58，该精度与文献［52］中通过学习实验寿命与理论寿命的对数差的精度几乎一致。因此，直接使用BNN对实验寿命进行学习也能得到较好的结果。

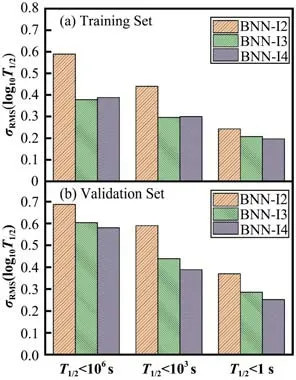
图1 训练集(a)和验证集(b)中三种神经网络BNN-I2、BNNI3和BNN-I4计算的β衰变寿命与实验值的均方根偏差σRMS(lgT1/2)Fig.1 RMS deviations from experimental data σRMS(lgT1/2)calculated by BNN-I3, BNN-I4, and BNN-I5 approaches for training set (a) and validation set (b)

为更细致地检验神经网络方法的预言能力，图2 给出了三种神经网络对Sn 同位素的预测结果，作为对比，图中还相应地给出了来自NUBASE2020的实验寿命（Experimental half-lives，Exp），用黑色方块表示。由图2可见，在已知核区域，BNN-I3和BNNI4 比BNN-I2 更好地再现了实验寿命。当外推至未知核区域时，BNN-I4 方法比BNN-I3 方法的误差范围要略小。此外，BNN-I3 方法在N=90~100 区域缓慢振荡上升，通过在神经网络输入层引入与对效应相关的物理量δ，BNN-I4 对β 衰变寿命的预测值与其他理论模型的结果更为相近（图3），这可能说明引入δ有助于神经网络更好地描述未知区域原子核的β衰变寿命。因此，下面将只展示基于BNN-I4方法的预测结果。

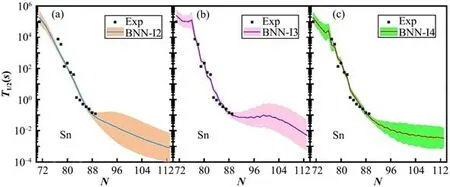
图2 BNN-I2、BNN-I3、BNN-I4方法预测的Sn同位素的β衰变寿命与误差[5]Fig.2 Nuclear β-decay half-lives and errors for Sn isotopes predicted by BNN-I2, BNN-I3, and BNN-I4 approaches[5]

图3 BNN-I4预测的Ni、Sn、Pb同位素链的β衰变寿命与RHB+QRPA、FRDM+QRPA、SHFB+FAM、SHFB+QRPA和WS4+GT理论结果的比较Fig.3 Comparison of nuclear β-decay half-lives of Ni, Sn, and Pb isotopic chains predicted by BNN-I4 with the theoretical results of RHB+QRPA, FRDM+QRPA, SHFB+FAM, SHFB+QRPA, and WS4+GT

为了进一步研究BNN-I4 方法的预言能力，图3和图4 分别以Ni、Sn、Pb 同位素链及N=50、82、126同中子素链为例，展示了BNN-I4方法与Relativistic Hartree-Bogoliubov（RHB）+QRPA［17］、Finite-Range Droplet Model（FRDM）+QRPA［54］、Hartree-Fock-Bogoliubov model with Skyrme force（SHFB）+Finite-Amplitude Method（FAM）［55］、SHFB+QRPA［56］、WS4+GT［57］模型结果的比较。可以看出，在已知核区，BNN-I4方法的预测结果与实验数据吻合较好，而其他理论模型的预言结果与实验数据偏差相对较大，对于质量较轻的原子核，如Ni 同位素链和N=50 的同中子素链，理论模型一般高估了实验寿命。因此，对于质量较轻的原子核，BNN-I4方法对远离稳定线原子核的预测寿命显著短于其他理论模型的结果。然而，随着原子核质量的增加，BNN-I4 对远离稳定线原子核的预测寿命与其他微观理论模型的结果非常接近。此外，BNN-I4方法预测的不确定度随着离已知核区的距离逐步增加。研究还发现，Ni同位素链的预测结果在N=56~58 区域突然上升，这与文献［52］中的结果类似。然而，由于这些原子核BNN预言的寿命不确定性很大，未来对该核区附近原子核衰变寿命的测量有助于确认这种现象是否真实存在。

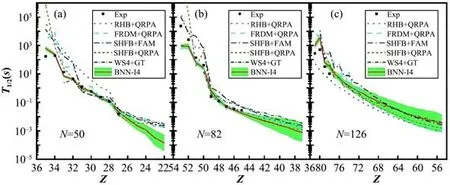
图4 BNN-I4预测的N=50、N=82和N=126同中子素链的β衰变寿命与RHB+QRPA、FRDM+QRPA、SHFB+FAM、SHFB+QRPA和WS4+GT理论结果的比较Fig.4 Comparison of nuclear β-decay half-lives of N=50, N=82, and N=126 isotonic chains predicted by BNN-I4 with the theoretical results of RHB+QRPA, FRDM+QRPA, SHFB+FAM, SHFB+QRPA, and WS4+GT

图5给出了核素图上原子核β 衰变寿命的实验数据与BNN-I4方法预测值的对数差。可以看出，与实验偏差大的原子核主要集中在稳定线附近，即寿命较长的原子核。这些原子核衰变寿命的计算对模型参数和衰变能Qβ都非常敏感，因此，与其他核模型类似，BNN-I4方法对稳定线附近原子核衰变寿命的描述也相对较差。幸运的是，这些原子核的寿命可以直接从实验测得。对远离稳定线的短寿命原子核，神经网络对β衰变寿命预测的偏差都在0.5个数量级之内。此外，BNN-I4 方法对于Z≳82 的原子核衰变寿命的预测值与实验值偏差较大，这可能由于该核区原子核β衰变寿命的实验数据过少所导致。

图5 核素图上实验值与神经网络BNN-I4对β衰变寿命预测值的对数差分布Fig.5 Logarithmic difference distribution on the nuclear chart between the predicted β-decay half-lives by BNN-I4 and experimental data

为了比较BNN-I4 方法预测的β 衰变寿命与理论模型预测值的差别，图6以WS4+GT模型为例，展示了BNN-I4方法的预测值与该模型预测值的比较。可以看出，BNN-I4方法的预测值与WS4+GT的模型预测值的偏差一般在1 个数量级之内。具体来说，在Z≲50 的区域，BNN-I4 方法在未知核区域的预测结果与理论值的偏差较大，而在Z≳50 的区域，尤其是远离稳定线的范围，BNN-I4 方法的预测值与WS4+GT的结果符合较好，从图3和图4也可得到一致的结论。虽然BNN-I4 方法从Z=20~50 之间远离稳定线核区域的预测结果与模型预测值有较大的偏差，但其在已知核区域的寿命预测有很高的精度，因此，其在未知核区的预测值可能具有较高的可信度。此外，利用BNN方法可以大规模计算原子核的β衰变寿命，进而为r-过程研究提供核物理输入量，因此，对理解宇宙的重元素起源具有重要意义。

图6 BNN-I4方法预测的β衰变寿命与WS4+GT模型预测值的对数差Fig.6 Logarithmic difference of β-decay half-lives between the BNN-I4 predictions and theoretical results of WS4+GT

3 结语

综上所述，本文采用了基于贝叶斯神经网络的机器学习方法，通过直接学习原子核β 衰变寿命的实验值，精确地预言了原子核的β衰变寿命，并给出了合理的不确定性评估。研究发现，在输入层引入β衰变能Qβ和与原子核对效应相关的物理量δ，输出层采用β 衰变寿命的对数，不仅可以显著提高神经网络方法的学习精度，外推至未知核区域，其预测值与其他微观理论模型的结果也更为接近，尤其是Z≳50 的原子核。然而，对于轻质量原子核，尽管其在未知核区预言的寿命短于核理论模型的结果，但是其在已知核区的寿命预测仍有很高的精度。未来将进一步发展考虑更多物理效应或物理约束的机器学习方法，提高机器学习对原子核β 衰变寿命的预言能力，着重关注其对轻质量原子核β 衰变寿命的描述，为核合成研究提供更精确的核物理输入量。

作者贡献声明所有作者都对研究构想和设计作出了贡献；材料准备、数据收集和数值计算由李伟峰、张晓燕和牛中明完成；初稿由李伟峰撰写；张晓燕和牛中明对初稿进行修改；所有作者阅读并批准最终稿。