基于热/力试验的折叠舵连接刚度与颤振分析
任浩源,王毅,王亮,周剑波,常汉江,蔡毅鹏,雷豹,张炜群
中国运载火箭技术研究院, 北京 100076
高速飞行器为适装新型发射平台和实现更远航程的指标要求,需要采用更大的翼/舵面以进一步提高升阻比。然而受限于发射平台的几何相容性约束,以及翼/舵面气动特性引发的控制稳定裕度不足问题,需采用翼/舵折叠技术[1-3]。根据翼/舵折叠的目标和功用,可将折叠技术发展划分为2 个阶段:在早期飞行器研制中,通过将飞行器翼/舵面预折叠,以缩减飞行器横向尺寸,提升储运能力,实现飞行器小型化,主要应用于航母舰载机、无人机、筒式发射导弹等传统航空器领域[4-5]。20 世纪90 年代以来,翼/舵折叠技术的优势进一步显著,通过调整折叠角度可有效改善飞行器气动特性,扩大飞行包线,增强控制能力,提升对不同环境和飞行任务的适应性,并已逐步应用于新概念飞行器、高速武器,以及返回式轨道再入航天器等[6-7]。目前,运用翼/舵折叠技术的新型飞行器研制得到了世界各国的高度重视,是当前航空航天领域研究的热点[8-10]。
与以往整体舵面相比,飞行器折叠舵的铰接锁紧机构因存在间隙和摩擦效应,呈现出“非线性、强不确定性、强时变性”动力学特征[11-13]。在此基础上,新型飞行器在大气层内长时间高马赫数飞行,高速气流被翼/舵前缘和折叠区激波压缩减速,并在表面边界层黏性作用下产生局部上千摄氏度高温环境[14]。由于折叠机构需同时实现力学承载和折/展作动,对材料的力学性能、加工特性以及配合精度要求很高,当前技术手段尚难以将折叠与防热功能集成于一体。这意味着局部铰接锁紧结构不可避免地长时间暴露在高热流和大载荷环境中,且难以实施有效的热防护措施,面临更为严酷的气动加热考验。因此,准确预报极端高温环境下连接机构非线性力学行为,揭示力/热多因素耦合影响下折叠翼/舵的运动规律,已经成为新型飞行器研制面临的关键科学问题。
目前国内外已有许多学者致力于折叠翼/舵气动弹性问题研究,并取得了一系列研究成果和进展[15-19]。Hu 等[20-21]基于刚柔耦合多体动力学方法和偶极子网格法,建立了折叠翼气动弹性模型,并对展开过程的动态响应和稳定性进行研究,给出了非定常和准定常分析方法的适用范围。Cheung 等[22-23]采用理论模拟和风洞试验方法对民用客机翼尖小翼的气动弹性特性开展研究,分析了折叠角度、弹簧连接刚度等参数对翼面气动弹性响应和阵风载荷减缓的影响。Conti等[24]基于多体动力学方法分析了几何非线性对飞行器折叠翼梢稳态气动弹性响应的影响。He等[25]针对含间隙折叠舵的非线性热气动弹性问题进行研究,基于热环境模拟装置开展了高温热模态试验,分析了高温材料弹性模量改变和热应力对折叠舵颤振特性的影响。
以上研究表明,大量折叠翼/舵研究集中于低速领域,关于折叠机构非线性力学行为对翼面气动弹性影响的理论和试验研究已经较为成熟,并已成功指导工程领域设计。但仍需要进一步阐述:①对于高速飞行器折叠翼/舵系统,折叠机构的间隙、材料特性还因飞行过程的热积累进一步改变,而现有研究较少表征温度对折叠系统连接刚度特性的影响;②已有研究主要依赖地面模态试验辨识或经验假设来确定折叠机构的连接刚度,尚未完善建立具体折叠机构形式与非线性刚度模型、待定参数选取的关系,并且关于工程中的实际铰接锁紧机构在极端高温环境下连接刚度力学模型的研究也比较有限。
由于高马赫数风洞对试件尺寸的要求,目前尚难以通过风洞试验模拟分析极端飞行工况下全尺寸翼/舵的气弹特性[26],因此高精度数值计算手段对高速飞行器设计具有重要作用。随着计算结构动力学(Computational Structural Dynamics,CSD)与计算流体力学(Computational Fluid Dynamics,CFD)技术的不断发展,将CSD与CFD 相结合的数值分析手段逐渐成为了解决高速飞行器气动弹性问题的新趋势,并已取得了大量研究进展[27-30]。马砾等[31]采用基于代数变换方法的网格变形技术和Timoshenko 梁模型,对直升机弹性旋翼非定常气动载荷进行求解。Chen 等[32]以高速飞行器机翼结构为分析对象,采用自适应时间步长方法、混合插值策略以及网格变形方法,研究了气动热对结构固有振动特性和气动弹性行为的影响。沈恩楠等[33]为了研究高速全动翼面在飞行剖面下的气动弹性问题,建立了多物理场全时域耦合分析方法,并给出了翼面热气动弹性稳定性分析流程。
折叠舵非线性特性问题的主要难点是气动加热环境下折叠机构的连接刚度难以准确描述。为了解决实际工程中非线性连接的折叠舵气动弹性问题,本文首先建立了综合考虑温度、载荷、机构间隙、摩擦等物理特性的折叠机构连接刚度力学模型,并进行试验验证;其次,采用准定常模型和工程算法,对飞行剖面中典型高度下的舵面气动弹性稳定性进行评估;最后,采用CFD 和CSD 耦合计算,开展时域气动弹性响应分析。
1 折叠舵与铰接锁紧机构
折叠舵系统采用根部折叠形式,分为内舵面和可折叠的外舵面,均采用耐高温合金钢结构。内舵通过舵轴与飞行器尾舱及伺服机构连接,外舵面与内舵面通过铰接锁紧机构连接,如图1所示[34-36]。
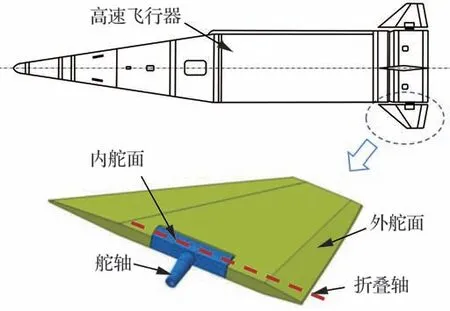
图1 类SS-23 飞行器[34]与折叠舵[35-36]示意模型Fig.1 Schematic models of SS-23-like[34] high-speed vehicle and folding fin[35-36]
折叠机构主要部件包括内舵组件、外舵组件、折叠转轴、锁紧销、扭转驱动扭簧和锁紧驱动弹簧,简化示意模型如图2 所示[35-36]。内舵组件与外舵组件由转动副配合连接,以限制外舵平动自由度以及除绕转轴方向外的转动自由度。展开信号指令发出后,外舵面在转轴处扭簧驱动下绕折叠轴转动,当展开至内舵孔与外舵孔相平齐时,锁紧销在驱动弹簧的作用下插入内孔,完成展开状态的锁紧。
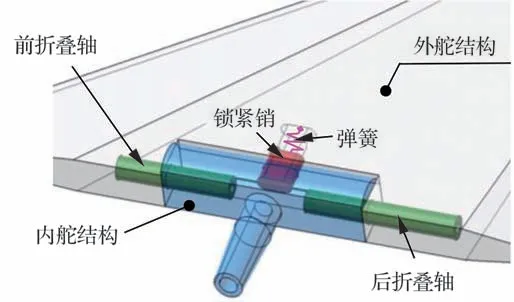
图2 折叠机构[35-36]示意模型Fig.2 Schematic model of folding mechanism[35-36]
2 连接刚度建模
连接机构存在间隙、摩擦等多种非线性因素,详细的作用机理为微观力学行为,对于工程实际机构难以具体量化分析。间隙、摩擦对连接机构的影响一般体现在等效刚度上,其核心是如何获取考虑非线性效应的刚度参数。传统工程化处理时,将内、外舵连接机构设为等效弹簧,刚度系数的确定需要采用人为假设法,或采用根据试验结果拟合的方法。对于新型飞行器设计,缺乏经验数据和试验数据的支撑,有必要根据具体结构形式提出一种考虑间隙、摩擦等非线性因素作用下的等效连接刚度获取方法。
2.1 模型简化
舵面气动载荷引起的弯矩和剪力全部由折叠系统传递至内舵结构。垂直于舵面的法向气动力是折叠舵的主要加载形式,绕折叠轴转动方向的刚度是工程设计人员关注的重点。因此将连接刚度定义为:气动力对折叠转轴的力矩M与外舵面绕折叠轴转动角度θ的改变量比值,并通过M-θ关系曲线表征。
外舵绕折叠转轴的转动刚度由两部分线刚度耦合形成:折叠轴处的支撑线刚度和锁紧销的支撑线刚度,如图3 所示。图3(a)给出了锁紧机构的各部件之间的接触关系,折叠转轴与内舵孔、外舵孔接触承载,锁紧销与内、外舵孔壁面接触承载。

图3 折叠舵连接刚度等效方法示意图Fig.3 Schematic diagram of equivalent method for connection stiffness of folding fin
为了对模型进行简化,将转轴的支撑承载等效为转轴中心的线弹簧,定义弹簧刚度为kaxis;将锁紧销的支撑承载等效为锁紧销孔中心的线弹簧,定义弹簧刚度为kpin。因此,求解连接刚度的核心为获得线弹簧的刚度。由于非协调接触属于局部力学行为,连接刚度主要受局部区域影响,因此刚度分析只需切取局部进行分析。图3(b)给出了从结构体中切取的转轴支撑分析模块和锁销支撑分析模块,固定内舵面,加载外舵面,通过载荷-位移关系即可获得实际工程结构的非线性弹簧刚度。
2.2 平动连接刚度
2.2.1 模型建立
针对含间隙局部结构开展非线性有限元分析,本质上是通过接触检测算法搜寻各部件接触区域,运用拉格朗日乘子法或罚函数法将接触界面的单边约束条件引入求解方程,采用“试探-校核”迭代方法获得接触状态随时间的演化过程[37]。转轴装配体和锁紧销装配体的有限元模型如图4 所示。

图4 有限元模型Fig.4 Finite element model
1) 转轴装配体模块包含内舵结构、外舵结构和折叠轴,如图4(a)所示。采用8 节点线性六面体单元(C3D8I)离散,单元总数为10 650。约束内舵对称面x方向自由度,约束内舵表面①的y和z方向的自由度,因此内舵的刚体自由度被约束;将外舵表面②节点的自由度与参考控制点进行耦合,并约束参考点除z方向以外的自由度。对参考点施加z方向载荷,利用参考点被施加载荷与z方向位移的关系曲线来表征转轴处的支撑线刚度。
2) 锁紧销装配体模块包含内舵孔、外舵孔和锁紧销,如图4(b)所示。采用8 节点线性六面体单元(C3D8I)离散,单元总数为8 743。约束内舵结构表面③节点的x,y和z方向的自由度;将外舵结构的表面④、表面⑤与参考控制点耦合,并约束参考点除z方向以外的自由度。对参考点施加z方向载荷,利用参考点被施加载荷与z方向位移的关系曲线来表征锁紧销处的支撑线刚度。
在工程结构中,转轴、孔、锁紧销均存在间隙,依据实际设计要求考虑间隙为1 mm。在有限元模型中分别定义内舵、外舵和转轴的接触关系。将两接触体分别记作A和B,将表面tSA和tSB相互临近或接触的2 个点记作接触点对。法向接触特性采用硬接触,即接触体在运动中不允许相互贯穿,t时刻接触点对的距离tgN满足[38]
式中:txA和txB分别为t时刻接触体A和B表面点的坐标;t gN的下标N 代表其在法线方向tnB上度量。
接触点对的法向接触力和为压力,表达式为
切向接触采用库仑(Coulomb)摩擦模型,切向摩擦力应满足
各结构均采用高温合金钢材料,密度为8 240 kg/m3,热物性参数及高温力学性能参数如表1 所示。采用直接法和牛顿迭代进行非线性求解,开启自适应步长加载策略。
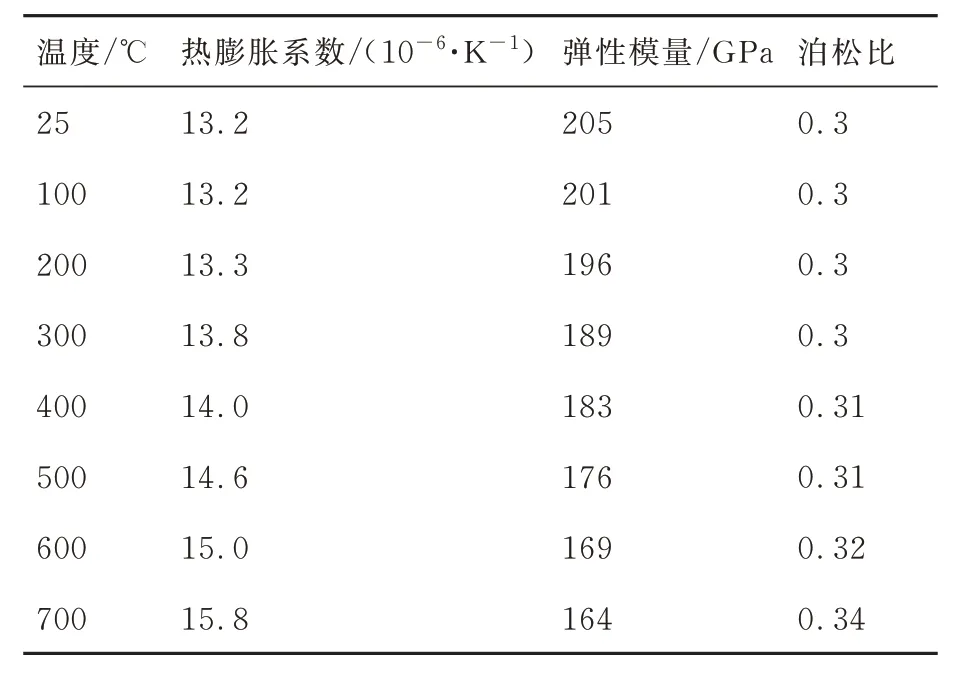
表1 高温合金钢性能参数Table 1 Properties of high-temperature alloy steel
2.2.2 平动连接刚度结果
为了模拟不同飞行载荷条件对机构连接刚度的影响,共设置了9 组载荷工况:100、200、300、500、1 000、2 000、5 000、10 000、20 000 N;5 组温度工况:常温,200、300、500、700 ℃。
图5 和图6 分别给出了常温条件下转轴和锁紧销处的载荷-位移关系曲线。为了便于计算结果对比,采用预加载措施消除机构间隙空行程的影响。将工况1(载荷为100 N)条件下的位移结果作为空行程,转轴处空行程位移为1.004 8 mm,锁紧销处为0.979 5 mm,并在载荷-位移曲线中扣除。采用二次函数对曲线进行分段拟合,通过求解曲线在不同载荷点的切线斜率,获得各工况的连接刚度数据,如表2 所示。
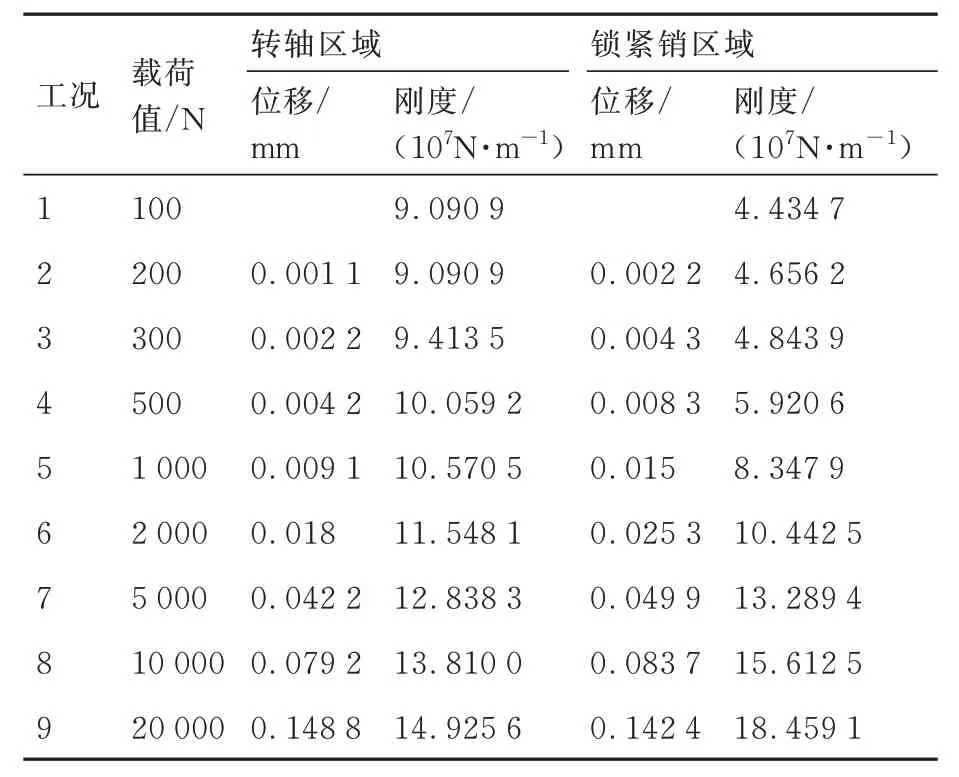
表2 不同载荷作用下转轴和锁紧销位置的位移及等效支撑刚度(常温条件)Table 2 Displacement and equivalent support stiffness at the position of shaft and locking pin under different loads (room temperature)

图5 转轴位置的支撑力与线位移曲线Fig.5 Relationship of support force and linear displacement at position of rotating shaft
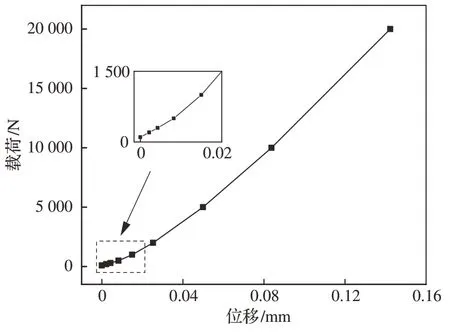
图6 锁紧销位置的支撑力与线位移曲线Fig.6 Relationship of support force and linear displacement at position of locking pin
分析可知:
1) 随外载荷增加,结构呈现“渐强弹簧”非线性刚度特性。其原因为初始条件下各部件之间为线接触,而随载荷增大,结构发生局部变形,接触区面积增大,接触刚度相应增大。
2) 对于转轴的支撑刚度,以100 N 载荷时的线刚度(9.09×107N/m)作为基准值,20 000 N 条件下刚度为14.93×107N/m,相比增长了64.2%;对于锁紧销位置的支撑刚度,以100 N 载荷下的线刚度(4.43×107N/m)作为基准值,20 000 N 条件下刚度为基准值的4.17 倍,因此锁紧销位置的支撑刚度对载荷更加敏感。
采用随温度非线性变化的材料热物性参数及高温力学参数,依照给定温度条件分别对结构整体施加均匀预温度场,再施加载荷开展力学分析,获得高温条件下折叠机构转轴和锁紧销处的位移和连接刚度特性。
图7 和图8 分别给出了在不同温度下转轴区域和锁紧销区域的载荷-位移曲线,表3 给出了连接刚度数据。
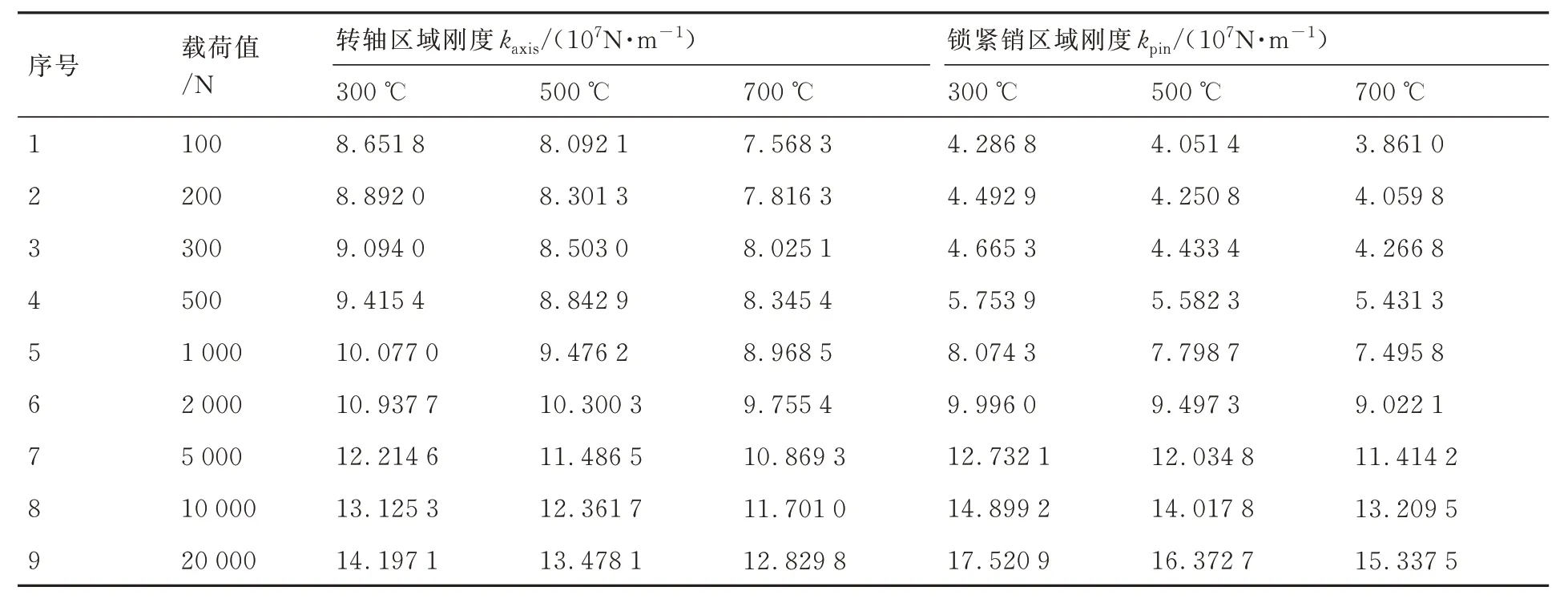
表3 不同温度下转轴和锁紧销位置的等效支撑刚度Table 3 Equivalent support stiffness of shaft and locking pin at different temperatures

图7 不同温度下转轴位置的支撑力与线位移曲线Fig.7 Relationship of support force and linear displacement at position of rotating shaft at different temperatures
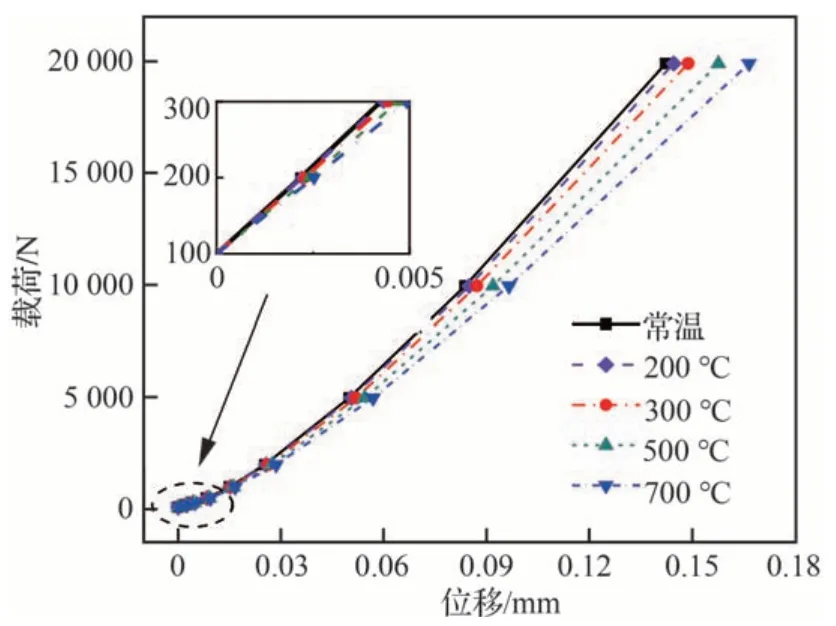
图8 不同温度下锁紧销位置的支撑力与线位移曲线Fig.8 Relationship of support force and linear displacement at position of locking pin at different temperatures
分析表明:
1) 在不同温度条件下获得的支撑力与线位移关系曲线,均呈现随载荷增大曲线斜率增大的“渐强弹簧”非线性刚度特性。
2) 随温度升高,连接刚度下降。若以100 N载荷常温工况作为基准值,在700 ℃温度条件下,转轴区域和锁紧销区域的连接刚度分别下降了16.7%和12.9%,说明高温对折叠机构连接刚度的影响不可忽视。
在热/力联合分析中,温度对结构力学性能的影响可主要归纳为材料弹性模量改变和热膨胀效应引起的热应力。对于本文折叠机构,热膨胀还导致部件之间的配合间隙量改变。
为了深入讨论温度对连接刚度的影响机理,针对锁紧销区域,将材料弹性模量下降和热膨胀2 个因素进行分离,建立如下分析模型。
模型1:仅考虑材料高温弹性模量削弱的模型。
模型2:仅考虑高温热膨胀效应的模型。
模型3:同时考虑弹性模量变化和热膨胀效应的模型。
采用700 ℃高温条件,计算各模型的支撑力与线位移关系曲线,并与锁紧销常温模型的曲线进行比较,如图9 所示。
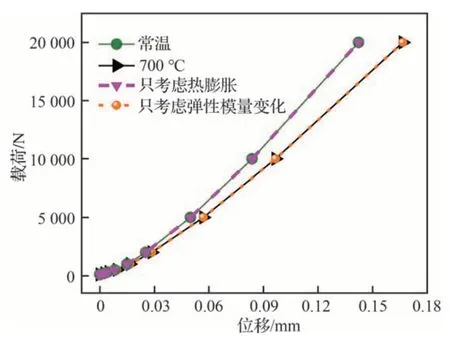
图9 高温条件下考虑不同因素的支撑力与线位移曲线Fig.9 Relationship of support force and linear displacement considering different factors at high temperature
分析可知:
1) 仅考虑高温热膨胀效应的曲线与常温曲线接近,说明热膨胀效应对连接刚度的影响不明显。这是由于锁紧销区域结构采用了均匀温度场和局部固支边界条件,热膨胀引起的热应力可通过自由表面进行释放[25];而热膨胀引起的配合间隙量的改变远小于部件之间的预置间隙量,可近似忽略其影响,关于间隙对连接刚度的影响分析可进一步参考文献[39]。
2) 仅考虑高温弹性模量削弱效应的曲线与同时考虑两个因素的曲线基本一致,说明支撑刚度的下降由材料高温弹性模量削弱因素主导。
2.3 转动连接刚度
在获得转轴和锁紧销处的支撑线刚度后,需要进一步将线刚度进行耦合,获得外舵面绕折叠轴转动方向的角刚度。由于本文分析的舵面本体刚度大于连接结构的刚度,将外舵面结构假设为准刚体,则外部气动力可以向舵轴与折叠轴交点处简化,得到z方向集中力Fz,绕x轴力矩Mx和绕y轴力矩My,如图10 所示。
建立外舵面z方向力学平衡方程:
外舵对折叠轴的力矩平衡方程为
外舵对舵轴的力矩平衡方程为
基于外载荷分布得到合外力Fz和力矩Mx、My,再求解式(4)~式(6),获得各等效弹簧的载荷Fspri和变形量uzi。进一步采用空间投影方法,将外舵面的法向量b投影至yOz平面,得到矢量p。计算表达式为
式中:A为yOz平面基向量构成的矩阵,表达式为
提取矢量p与Oz轴夹角作为外舵面绕折叠轴转动的角度θx,则Mx-θx曲线即可表征锁紧条件下折叠机构的连接刚度。
2.4 试 验
为了探究锁紧条件下折叠机构的连接刚度特性,验证所建立的计算模型的正确性,分别开展常温力学试验以及高温热/力联合试验。
2.4.1 试验装置
热/力联合试验系统由辐射式热环境模拟子系统和加载子系统构成:热环境模拟子系统采用石英灯阵列生成高温热环境,如图11 所示。通过实时控制石英灯加热阵列的驱动功率,实现对折叠舵表面热流快速、准确的动态模拟;力学加载子系统按照预先设定的载荷条件,并配合温度控制子系统,实现对高速飞行器折叠舵的热/力联合环境的综合生成。
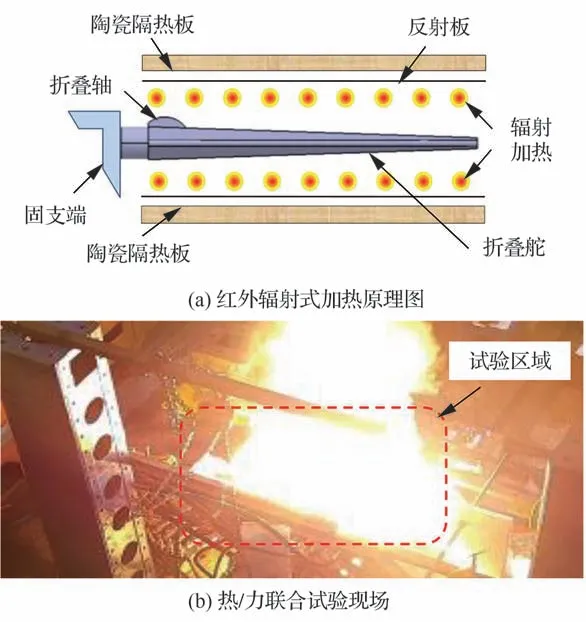
图11 试验装置Fig.11 Experimental facility
试验中,将舵轴固定于试验台,空气舵表面采用石英灯阵列加热,采用伸长杆对高温环境下的折叠舵进行加载。为了更好地模拟舵面不同部位的飞行热环境,采用CFD 软件对飞行过程中的热流分布进行计算,将舵面热流划分楔形前缘区和平面区,并依据热流分布特点对舵面进行加热。在试验中,温度控制系统通过各分区中心安装的热流传感器对加热过程进行闭环控制,使各表面热流按照预设加热历程变化,采用高温热电偶实时测量各区域的温度。
2.4.2 试验结果及与理论值对比分析
1) 常温试验
将舵面划分为前锥面、平面和后锥面共3 个区域,在各分区施加集中力(F1~F5)以模拟飞行中的分布气动载荷,加载位置及编号如图12 所示。在试验中,应保证各加载点的总载荷Fz以及力矩Mx、My与飞行工况一致。综合考虑飞行器的“速度-高度”剖面、机体姿态以及舵面偏角等因素,确定外舵面最大飞行载荷为Fz=15 000 N,Mx=1 450 N·m,My=200 N·m。

图12 试验加载点与位移测点Fig.12 Loading position and displacement measuring position in test
为了比较不同载荷对连接刚度的影响,试验中采用台阶式加载方式,将加载过程设计为12 级,最小试验载荷为0.1Fz,最大试验载荷为1.2Fz(考虑安全系数为1.2),待每级加载和位移响应稳定后,再继续开展下一级载荷试验。在外舵表面布置6 个位移测点(M1~M6),分布在沿舵展长方向的3 个剖面(Sec1~Sec3),在试验全程实时测试并记录各点的位移响应。
对外舵面采用准刚体假设,依据刚体动力学可知:对于含间隙折叠舵面,在外载荷作用下舵面姿态角可分解为先绕折叠轴转动θx,再绕舵轴扭转θy。为了对转角进行解耦,定义舵轴延长线与展向各剖面(Sec1~Sec3)交点为位移特征点(P1~P3),特征点仅包含舵面绕折叠轴转动产生的位移。在获得试验数据后,先对各剖面测点的位移数据进行插值,获得特征点的位移,再基于特征点(P1~P3)位移分别辨识外舵面绕折叠轴转动的角度。
图13 分别给出了不同载荷作用下外舵面“力矩-转角”的计算曲线与试验曲线,表4 给出了绕折叠轴的转动刚度,其中KθT为转动刚度的计算结果,KθE1~KθE3分别为基于特征点P1~P3辨识得到的试验结果,R1~R3为计算值与试验值的相对误差。由图13 和表4 可知,计算曲线与试验辨识曲线整体上具有很好的一致性,证明了提出的刚度计算方法的正确性和可用性。

表4 折叠机构连接刚度Kθ的计算值、试验值及相对误差Table 4 Simulated value, experimental value and relative error of connection stiffness Kθ of folding mechanism
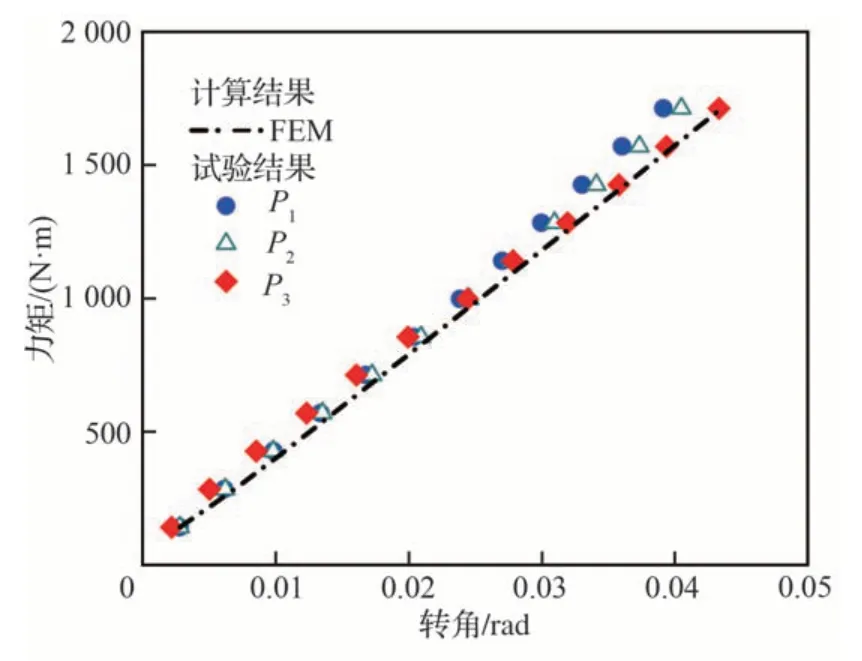
图13 载荷-转角曲线的计算值与试验辨识值Fig.13 Relationship of load and rotation angle by simulation and test identification
在初始载荷(Mx<290 N·m)条件下,转动刚度计算值与试验值的相对误差较大(最大值为R3=67.4%,Mx=145 N·m),这是因为小载荷阶段接触不稳定,由于机构存在配合间隙,加载中受各部件之间摩擦滑动特性影响。若精细刻画小载荷阶段的接触特性,需要对微观接触和演化进行预测,建立微观结构效应、接触区载荷分配与宏观连接刚度之间的关系,而基于宏观力学试验和仿真还不能全面获得。
在中等载荷(290<Mx<1 015 N·m)条件下,接触状态基本稳定,此时计算值与试验值的吻合性较好,相对误差最大不超过11.4%。
在大载荷(1 015 N·m<Mx)条件下,转动刚度计算值与基于特征点P1和P2辨识获得的刚度试验值稍有些偏离(最大值为R1=21.4%,Mx=1 305 N·m),这是由于计算和试验辨识中均将舵面视为准刚体,在小载荷下刚体假设和位移特征点处无扭转假设近似成立;而大载荷下,舵面在各载荷综合作用下产生复杂柔性变形(如弯曲和扭转等),折叠机构连接处的边界非线性与舵面自身柔性变形之间耦合,导致试验辨识误差累积。但是转动刚度的计算值与基于特征点P3辨识获得的试验值之间整体误差仍小于10%,最大误差不超过13.4%,具有很好的一致性。
2) 高温试验
高温热/力联合试验中不同时刻下的载荷与表面热流曲线如图14 所示。将载荷以基准飞行载荷(Fz)进行归一化,热流以峰值热流(Hmax)进行归一化。高温试验的力学加载点位置与常温时相同,基准载荷和弯矩分别为Fz=15 000 N,Mx=1 450 N·m,My=200 N·m。首先加载至0.8Fz,再加载至1.2Fz,再线性卸载至1.054Fz,最后保持固定载荷至试验结束。在加热过程中,舵面的前缘楔形区和平面区均存在3 个热流峰值。
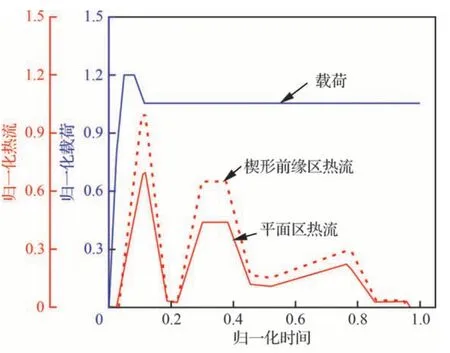
图14 高温热/力联合试验的载荷与热流输入Fig.14 Input of load and heat flow for thermalmechanical coupling test
图15 给出了不同时刻下锁紧销附近区域的实测温度响应曲线(T1~T3)。分析可知:① 结构温度响应具有滞后特性,在外表面升降交替、复杂时变非线性热流输入条件下,结构温度整体呈现上升趋势。② 在试验末秒时刻,结构温度呈现非均匀特性,其中T1温度传感器由于靠近舵前缘,最高温度达412.7 ℃;T3温度传感器靠近舵后缘,温度相对较低,末秒时刻温度为311.9 ℃。
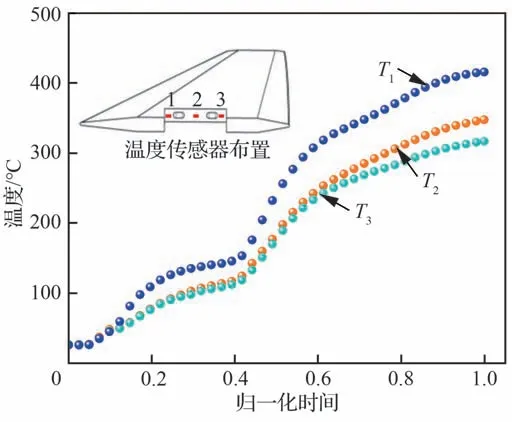
图15 不同时刻下折叠区域实测温度Fig.15 Measured temperature of folded area at different times
通过不同时刻的温度插值获得线弹簧刚度,再代入式(4)~式(8)计算得到外舵面绕折叠轴转角θx。图16 给出了不同时刻转角的计算值与基于特征点P3辨识的试验值,图17 给出了时变刚度曲线。
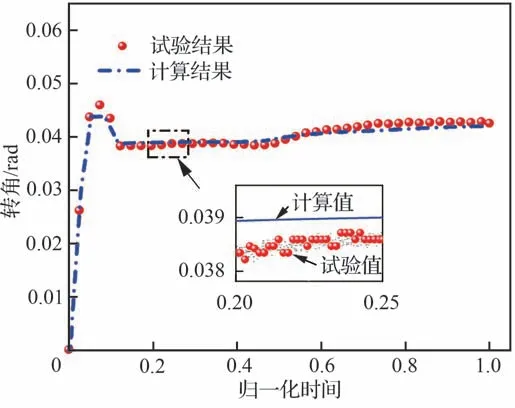
图16 热/力载荷下外舵面转角的试验与计算曲线Fig.16 Rotation angle of outer fin at different times by simulation and thermal-mechanical coupling test
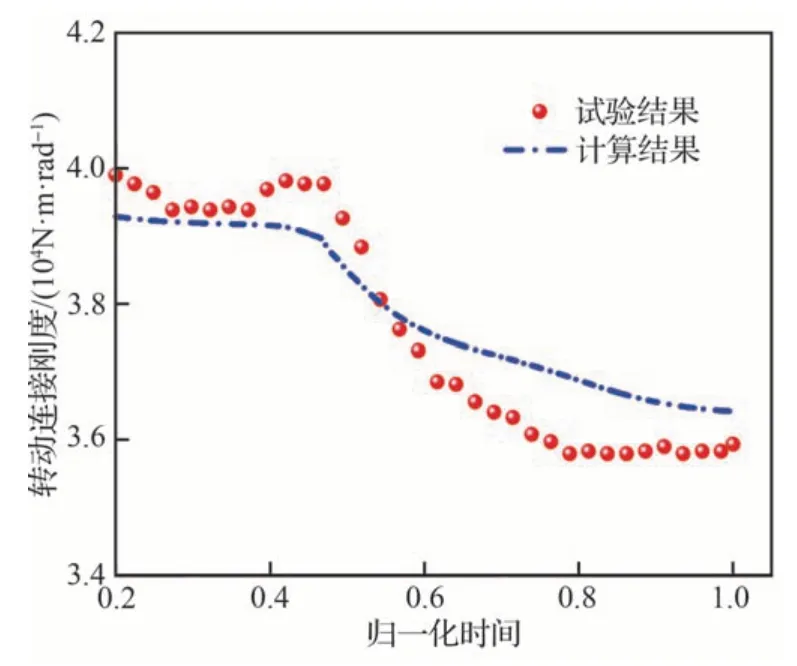
图17 高温连接刚度随时间变化曲线Fig.17 High-temperature connection stiffness at different times
由图16 和图17 分析可知:① 计算得到的转角曲线与试验转角曲线趋势一致,具有较好的一致性,在高温时间段(0.4tmax~1.0tmax)转角计算值与试验值之间的相对误差小于3%,连接刚度的计算值与试验值的相对误差小于4%,证明本文分析方法的有效性和可用性。② 热/力耦合分析中,基于试验辨识的末秒时刻高温刚度比初始时刻刚度下降了9.63%;理论计算的末秒时刻刚度较初始时刻降低了7.3%,说明高温材料弹性模量削弱对连接刚度具有显著影响,工程设计中应该予以重视。
3 热气动弹性耦合分析
3.1 热气动弹性稳定性分析
3.1.1 控制方程
目前在工程初步设计中,采用模态方法对结构模型进行降阶,运用修正三阶活塞理论建立非定常气动模型,基于特征值法进行气动弹性稳定性预测,以评估飞行器在不同飞行工况下的颤振特性。
对于折叠舵系统,不考虑结构阻尼时,物理坐标系下的运动方程为
式中:M、K和f分别为质量矩阵、刚度矩阵和舵面振动引起的非定常气动力向量;u为位移向量。
假设舵面按照简谐形式振动u=Ueλt,位移幅值向量U可表达为模态叠加形式,则颤振方程(9)可写为
采用修正的三阶活塞理论,则广义气动力向量的表达式为
式中:各参数表达式见文献[40-41]。
3.1.2 计算结果
1) 模态分析
基于有限元方法开展常温模态分析和400 ℃高温模态分析,如图18 所示。将内舵与外舵的孔洞填实,采用六面体网格C3D8R 剖分,网格数为36 990,分别赋予常温和400 ℃高温材料特性参数。
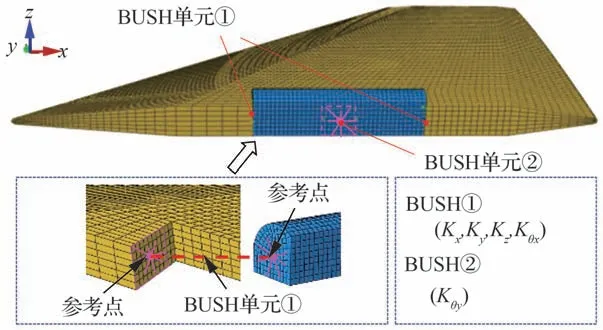
图18 折叠舵有限元模型Fig.18 Finite element model of folding fin
对于折叠区域的铰接锁紧机构,未单独建立模型,而是借鉴文献[25]中基于弹簧单元的等效方法。即分别将内、外舵的转轴区域节点的位移与控制点耦合,再建立控制点之间的弹簧约束关系。需要指出的是,文献[25]中刚性约束了内、外舵结构控制点的5 个自由度(x,y,z,Ry,Rz),仅保留了折叠转动方向的自由度Rx;本文对该方法进行改进,折叠转动方向的自由度Rx的弹簧约束不变,释放了5 个刚性约束,通过添加线弹簧(Kx,Ky,Kz)来提供等效约束,避免连接刚度约束过强导致外舵面的频率偏高。基于前文分析,常温下折叠机构线连接刚度值约为1×108N/m,转动连接刚度值约为3.9×104N·m/rad,400 ℃高温连接刚度约为常温值的90%(取包络设计)。因此,在有限元模型中综合考虑了高温环境中材料性能下降以及连接刚度改变。
舵轴与舱段及伺服机构连接的转动刚度基于同类型装置的历史数据获得,本文取为4.15×104N·m/rad[42]。
图19 分别给出了前8 阶固有频率ω和振型,其中频率下标R 代表常温25 ℃结果,下标H 代表高温400 ℃计算结果。分析可知:① 前两阶为刚体振型,分别为舵面绕折叠轴和舵轴的组合振动,第3 阶振型为舵面的面内振动,第4~8 阶为舵面弹性变形与边界约束共同影响下的组合振动。② 第4 阶和第5 阶的振型相似,第6 阶和第7 阶的振型相似,频率差异主要由于内、外舵连接刚度与舵轴-机体连接刚度之间的耦合。③ 随温度升高,固有频率下降约5%,主要由连接刚度和材料力学特性下降导致。
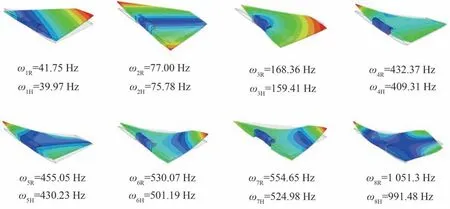
图19 常温及高温折叠舵模态特性Fig.19 Mode properties of folding fin at room temperature and high temperature
2) 气动弹性稳定性分析
依据飞行剖面,20 km 以下对应最大飞行动压,容易出现气弹发散。因此选择0、10 km 作为典型高度剖面,开展稳定性分析。不同高度气体物性参数如表5 所示。

表5 各高度剖面气体物性参数Table 5 Physical parameters of air at each altitude profile
图20 给出0 km 高度下,基于常温和400 ℃高温模态参数计算的V-g和V-f曲线,其中V代表飞行速度,g代表人工结构阻尼系数,f代表振动频率。图21 给出10 km 高度下的计算结果。由图中曲线可知,颤振形式主要为一阶模态和二阶模态耦合,且高温提高了颤振速度。

图20 0 km 高度的V-f 及V-g 曲线Fig.20 ‘V-f’ and ‘V-g’ curves at 0 km altitude

图21 10 km 高度的V-f 及V-g 曲线Fig.21 ‘V-f’ and ‘V-g’ curves at 10 km altitude
为了进一步探讨温度升高对折叠舵颤振特性的影响机理,采用0 km 高度气体物性参数条件,分别将常温、高温的连接刚度与常温、高温的舵面本体模型进行组合,形成4 种模型条件,计算各模型的颤振速度。表6 给出了颤振速度计算结果,其中KR代表常温连接刚度,KH代表高温(400 ℃)连接刚度。
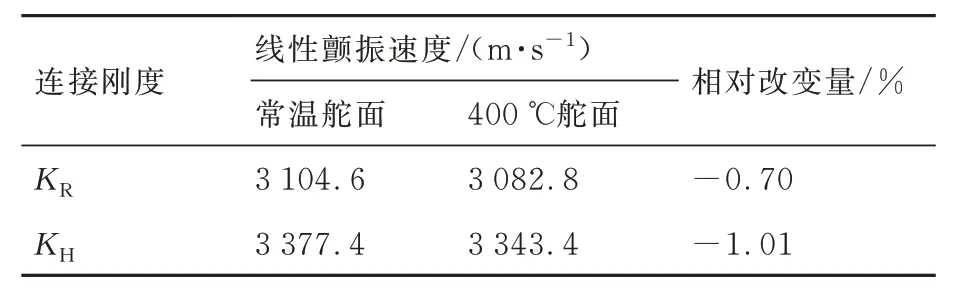
表6 不同温度舵面本体和连接刚度组合模型颤振速度Table 6 Flutter velocity of combined model of fin body and connection stiffness at different temperatures
对表6 分析可知:针对本文所分析的折叠舵研究对象,高温对于颤振特性的影响应该同时考虑舵面本身的刚度下降和连接刚度下降两个方面因素的共同作用,其中舵面本身刚度下降导致颤振速度下降,而连接刚度下降导致颤振速度升高。因此,高温条件下折叠舵面颤振速度的最终变化取决于哪个因素占主导。
3.2 气动弹性响应分析
采用STAR-CCM+软件[43]求解Navier-Stokes(NS)方程,采用k-ωSST 湍流模型和二阶隐式求解方法,计算时间步长为0.000 5 s,内迭代步数为50。图22 给出舵面的流体计算域、网格划分及边界条件。启用多重网格(Multigrid)以及网格序列化(Mesh-sequencing)方法进行收敛加速,网格总数为20 万。采用Abaqus 软件求解固体域,网格类型为C3D8R,并采用自适应步长的隐式动力学求解策略。当时域计算时,采用松耦合方法对结构动力学模块位移数据与CFD模块气动载荷进行交互,并运用径向基函数(Radial Basis Functions, RBF)动网格技术实现了流固耦合界面的迭代更新。
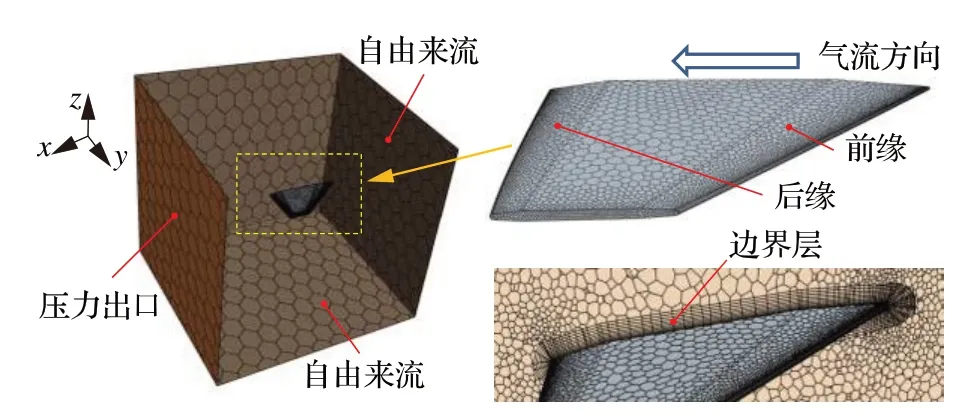
图22 舵面计算域及网格划分Fig.22 Computational domain and mesh of fin
针对0 km 高度剖面,图23 给出了Ma=1.5,1.8,2 飞行速度下的舵面监测点(2 个监测点分别位于舵梢前缘和后缘处)的法向位移响应曲线。计算结果表明:Ma=1.5 条件下监测点的位移响应呈现收敛趋势,Ma=2 条件下位移响应呈现发散趋势,而Ma=1.8 近似为临界稳定。需要指出的是,采用CFD 与CSD 耦合计算方法获得的临界颤振速度低于采用活塞理论的计算结果,采用基于NS 方程的流固耦合分析方法更加保守,文献[44-46]也报道了类似的结果。该现象的产生机理:在低海拔条件下,受边界层位移厚度(Displacement Thickness)的影响,舵面气动特性发生改变,黏性效应对舵面压力系数分布影响显著,而采用三阶活塞理论方法忽略了空气黏性,导致其颤振计算结果与基于NS 方程的CFD 方法计算结果偏差大[47]。本文基于活塞理论工程计算方法与基于CFD/CSD 耦合方法的颤振计算结果偏差源于活塞理论方法无黏性气体假设的局限性,且当两者结果存在差异时,CFD 方法计算结果更加准确。由于本文高速飞行器折叠舵在飞行末段的机动/俯冲时动压达到峰值(属于颤振风险点),高度相对较低,采用CFD/CSD耦合分析方法更为合适。

图23 不同速度下监测点的位移响应曲线Fig.23 Displacement response curves of monitoring points at different speeds
为了进一步分析气动弹性发散后的力学行为,图24 和图25 分别给出了Ma=5 条件下的网格变形结果和颤振发生后的结构振动响应形式。分析可知:① 采用径向基函数动网格生成方法能够有效适应振荡发散后的舵面构型,网格的变形能力强。② 颤振发生时舵面呈现俯仰和扑动耦合的振动模式。

图24 网格变形Fig.24 Mesh deformation

图25 气动弹性发散后的振动形式Fig.25 Form of vibration after aeroelastic divergence
4 结 论
1)建立了考虑间隙、摩擦、温度和载荷因素的连接刚度分析方法,解决传统折叠机构刚度设计对试验依存度高的问题,为工程中具体折叠机构的力学模型建立和刚度表征做出了贡献。
2)对平动连接刚度分析表明,随外载荷增加,支撑刚度呈现“渐强弹簧”非线性特性;若以100 N 载荷常温工况作为基准值,在700 ℃温度条件下,转轴区域和锁紧销区域的支撑刚度分别下降了16.7%和12.9%,说明高温对折叠机构连接刚度的影响不可忽视。
3)常温工况条件下折叠舵转动连接刚度计算值与试验值的整体相对误差小于10%,高温工况条件下相对误差小于4%,证明了分析方法的有效性和可用性。
4)基于CFD/CSD 耦合分析方法获得的颤振速度更加保守,释放了折叠舵颤振的风险。由于本文提出的流固耦合方法基于商业有限元软件,其计算鲁棒性和通用性强,可经过扩展后用于分析同类型折叠翼/舵结构,为飞行条件下舵面响应提供可靠、适用和有效的预测。

