基于数据同化的试验数据驱动的叶栅流场预测

刘锬韬，李瑞宇，高丽敏，*，赵磊

1．西北工业大学 动力与能源学院，西安 710072

2．西北工业大学 翼型、叶栅空气动力学国家级重点实验室，西安 710072

3．西安交通大学 航天航空学院，西安 710049

对航空发动机日益增长的高可靠性、高性能、高经济性的需求不断推动着发动机部件研制过程中流场预测技术的进步。压气机是航空发动机的压缩部件，起着对来流气体减速增压的作用，对航空发动机运行的性能、安全性和稳定性有重要影响。目前，压气机流场预测的主要方法有解析全尺度湍流的直接数值模拟（Direct Numerical Simulation，DNS）［1］、解析大尺度湍流的大涡模拟（Large Eddy Simulation，LES）［2-3］及基于雷诺平均 Navier-Stoke（Reynolds Averaged Navier-Stokes，RANS）方程的湍流模型［4］。DNS 和LES理论上较为完备，对湍流的刻画更为准确，可以获得流场中精细的流动结构，但其巨大的计算量及数据存储量令其在工程领域的应用极为有限，目前仅应用在前沿学术研究中；在近期，湍流模型凭借其计算量小、鲁棒性好、计算精度可以接受，仍将是工程领域中流场预测的主力军。但是，基于RANS 的湍流模型大多基于湍流各项同性的涡黏假设，在封闭雷诺应力项的过程中应用了大量的假设和经验参数，使湍流模型的计算结果都包含有较多的不确定性。这导致每种湍流模型都有一定的应用范围，且对于有强逆压力梯度和流动分离的复杂流场，湍流模型预测虽然能够反映一定的流动特征，但预测准确性相对较差。压气机内包含逆压力梯度、分离流及激波等复杂的流动现象，在一些非设计工况下，预测精度的问题比较明显。因此，采用各种方式提高航空发动机内湍流预测精度十分有必要。

一般认为，湍流模型计算结果的不确定主要来源于4 个方面［5］：① 雷诺平均过程；② 使用平均参数对雷诺应力的表示；③ 特性拟合函数的选择；④ 模型系数的确定。来源①虽然引入了不确定性，却是构造湍流模型的基础，一般难以修正。目前，通过改进湍流模型提高预测精度的研究主要有3 类［6］：① 直接由DNS、LES 或者试验数据校正数值流场中的雷诺应力；② 由湍流模型某一项进行修正；③ 对模型系数进行校准，分别对应不确定度来源的②、③和④。这类研究的思路一般有2 类：① 根据湍流理论和相关经验修正湍流模型；② 使用数据同化（Data Assimilation，DA）［7］方法利用高可信度的数据如DNS、LES 或试验测量数据校正RANS 流场和湍流模型。

DA 作为一种融合试验测量与模型预测结果的数学方法，最早起源于气象领域［8］，后被应用到海洋科学［9］和地球物理［10］等学科，主要用于将卫星或者地面站的观测数据融入预测模型，进行气象或者环境预测，近年来也被应用到湍流流动的增强预测［11］研究中。应用到湍流预测的DA 算法主要有2 类：① 伴随类算法；② 卡尔曼滤波类算法。伴随类算法可以对全场流动变量进行反演，使预测结果更贴近物理状态，但需要求解伴随方程以及改造CFD 求解器，在实现上比较复杂，主要用于学术研究；卡尔曼滤波类方法来源于经典的卡尔曼滤波算法，既可用于校正模型系数，也适合于全场参数重构，不侵入CFD 求解器，更适合工程应用。

Foures［12］和He［13］等使用基于伴随优化的数据同化方法为RANS 流场添加了额外力项以构造各项异性的湍流黏度。张亦知等［14］在S-A 湍流模型的生成项上添加了一个随空间分布的修正因子β，利用DNS 计算结果及物理知识约束，通过伴随方法确定了β的分布，提高了对方腔等流动摩擦阻力的预测精度。 Singh 和Duraisamy［15］使用贝叶斯推断结合离散伴随方法，使用DNS、LES 及试验数据对槽道、弯管和翼型等流场中湍流模型的生成项进行了校准，显著提高了边界层预测精度。但大部分的形式修正项仅为空间分布的函数，仅针对参与校准的流动有效，缺乏普适性。He 等［16］为提高S-A 模型对压气机失速裕度的预测精度，对模型方程的剪切应变力项乘以一个经验系数，该系数是压力梯度和速度旋度的函数，并在多个压气机算例上进行了测试，具有一定普适性。

湍流模型系数的默认值多数来源于平板、翼型等经典的湍流案例，在处理复杂流动时略显预测精度不足。但实际上，湍流模型本质上不能完整地刻画湍流，所以很难找到一组具有完全普适性的湍流模型系数，校正后的系数也具有流动依赖性，但在一定范围内具有适用性。

王丹华等［17-18］调整了S-A 模型中Cb1参数，改善了压气机叶栅角区分离的预测效果。马力等［19］将压力梯度引入到S-A 模型的剪切力系数中，亦改善了压气机叶栅角区分离的预测效果。但在根据经验调整模型系数时，试验数据仅用来验证效果，并未直接参与调整过程，参数选取和调整幅度主观性较强；而卡尔曼滤波类数据同化方法直接利用试验测量数据校正模型参数，客观性更强，且可以同时校正多个参数。

集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）方法是最常用的一种滤波类数据同化方法，由Evensen［20］从经典的卡尔曼滤波发展而来，EnKF 使用Monte-Carlo 方法构造样本协方差代替模型协方差矩阵，避免了复杂的公式推导，特别适用于Navier-Stokes 方程等复杂非线性模型。为了适合不同的应用场景和需求，EnKF 发展出了多个变种，如集合变换卡尔曼滤波［21］（Ensemble Transformed Kalman Filter， ETKF），考虑正则项的正则集合卡尔曼方法［22-23］（Regularized Ensemble Kalman Method， REKM）等。

Deng 等［24］使用EnKF 方法对4 种湍流模型参数在射流流场中进行了修正，原本与试验数据符合并欠佳的k-ω和SST（Shear Stress Transport）模型在经过系数校正后也可以较好地符合。房培勋等［25］使用EnKF 方法对蒸汽阀门流动中SST 湍流模型的系数进行了标定，有效提高通流特性预测模型的精度，并在相近工况具有一定普适性。Kato 等［26］使用ETKF 对翼型流场中SST模型a1参数进行了优化，认为a1=1.0 时比默认值0.31 能更好地预测分离流和逆压力梯度流动，并且认为在参数优化过程中应该考虑风洞壁面效应，将来流攻角和来流马赫数纳入校正过程中。

目前大部分基于试验数据的流场参数校准研究主要针对平板、圆柱绕流、槽道和翼型等经典流动，针对压气机流场的研究相对较少。压气机流动有其自身特点，如包含逆压力梯度、明显的流动分离、激波边界层作用等流动现象，且工程上压气机试验流场中测点稀疏，开展对压气机流动的增强预测研究，提高流场预测精度，对发动机部件设计和评估有重要意义。

由此本文基于集合卡尔曼滤波数据同化方法，开展了针对压气机叶栅的试验数据驱动的流场预测研究：首先，使用试验函数验证了EnKF 算法超参数的选取准则；然后，使用两步EnKF 数据同化方法，通过校正S-A 和SST 湍流模型系数及来流边界条件，对压气机叶栅进行由试验测量数据驱动的流场预测，实现了对试验工况流场的重构；最后，分析了叶栅的流动校正机理及校正系数的分布规律，比较了数据同化前后的流动差异。

1 集合卡尔曼滤波方法及验证

1.1 集合卡尔曼滤波方法

EnKF 是一种序列滤波方法，原本用于处理非定常系统，本文研究对象是定常流动系统，不同于文献［26］的伪非定常方法，本文对EnKF 进行简化，使其适用于定常系统，计算量亦有所减小。定常系统预测和观测过程可以描述为

式中：θ为来流马赫数、攻角和湍流模型系数等组成的模型系数向量；x为状态向量，在叶栅算例中x=[θT，MaIST]T，下角标“f”表示该状态向量为模型预测结果，MaIS为流场中对应叶栅风洞试验测量位置的叶片表面等熵马赫数；y为观测向量；ε为观测误差；M 为模型算子，即使用湍流模型的求解器；H 为观测算子，从状态向量中提取出试验测量位置相应的物理量。式（1）为预测过程；式（2）为观测过程。

对来流边界条件和湍流模型系数依试验工况和系数默认值θ0进行浮动，浮动过程使用拉丁超立方方法进行采样，生成一个包含N个样本的集合，记为θi，i=1，2，…，N，则每个样本均可获得一个预测结果：

构造样本协方差矩阵P、误差协方差矩阵R和卡尔曼增益矩阵K：

式中：wi为每个样本的系统噪声，一般为一组零均值正态分布的随机数，在确定其方差时，需同时考虑测量噪声和物理过程与预测模型的物理差异产生的偏差，比如本研究中试验过程为三维叶栅流动，预测模型为二维叶栅流场数值计算，以及湍流模型不能完全准确描述湍流流动，测量偏差的方差应该适当大于测量不确定度对应值。

对每个集合样本进行EnKF 校正，即对应卡尔曼滤波的分析步：

式中：yexp为试验测量数据。

在实际应用过程中，可以多次生成噪声，即对式（5）～式（8）多次计算，求取平均值，可以增加算法的稳定性，从而避免了像文献［24-25］中的多次内迭代，进一步减小计算量。

最后获得校正后集合成员的均值即为数据同化后的状态变量：

从中提取出新的入口边界条件和湍流模型系数θnew，代入求解器再进行一次CFD 计算获得完整的预测流场，其对应的状态变量xnew即为真实状态变量xtrue的最优估计。

以上为单步集合卡尔曼滤波的数据同化方法，输入数据为模型参数的初始值，输出参数为校正后的参数值。对于本文的研究对象，EnKF已经满足需求，故没有采用正则化方法。

1.2 基于测试函数的验证

为了验证算法代码编写的准确性、测试数据同化的效果以及探索超参数选取准则，使用简单数学测试函数对以上算法进行了验证，测试函数包含真实函数ytrue（x）和模型函数ym（x）：真实函数用以模拟真实的物理过程，其结构相对复杂；模型函数包含若干系数，表示对真实物理过程的简化和建模，结构相对简单。借鉴文献［27］中的测试函数，构造测试函数为

式中：自变量x∈［0，1］，为模拟观测过程，每隔0.1 长度取一个观测点，共11 个观测点；a、b、c、d为模型系数；初值取θ0=［a，b，c，d］=［6，2，12，5］。真实函数和初始模型函数如图1 所示。可以看出模型函数与真实函数形状相近，但数值上有较大差别。取状态变量为x=[θT，yobsT]T，其中yobs表示观测点处的预测值。

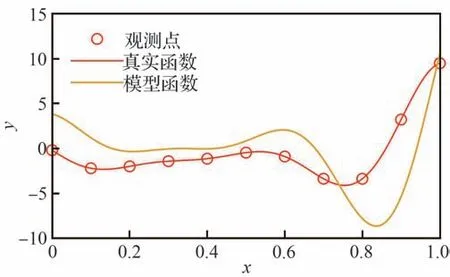
图1 测试函数图示Fig.1 Illustration of test functions

集合卡尔曼滤波的超参数主要有样本数量、参数浮动范围、噪声给定等。考虑到数据同化过程中的各参数中包含一定的随机成分，即便参数设置相同，每次数据同化的结果也会有微小差异，为确保评估的准确性、科学性，对同种参数设置进行多次重复计算，统计不同超参数设置的数据同化效果，综合考虑计算量和统计效果，设定每组超参数重复计算的次数为500，获取预测结果及中间变量的均值及标准差。当单一超参数改变时，其他参数均采取默认值，超参数默认值见表1。图2 显示了在默认参数下数据同化校正结果，可以看出数据同化后的结果明显更接近真实函数，从而验证了算法及代码的准确性，但也可以看出，当x＜0.5 时预测效果并没有明显改善，即单步的校正效果有限。

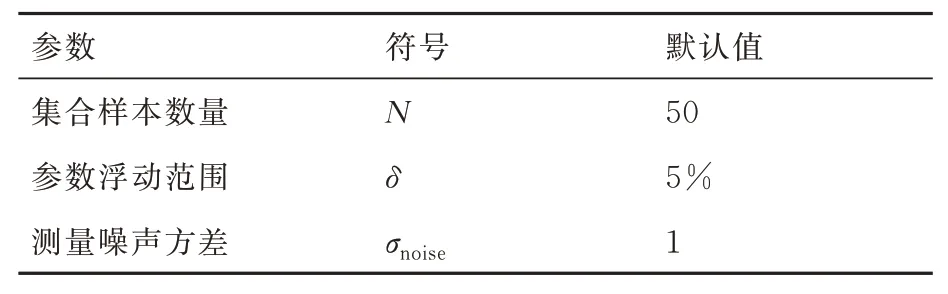
表1 超参数的默认值Table 1 Default values of hyperparameters

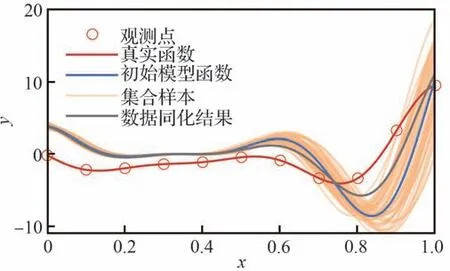
图2 默认参数下数据同化校正结果Fig.2 Result of data assimilation under default parameters

图3 显示了分别给定不同样本数N、参数浮动范围δ和噪声方差σnoise时的观测点及全局预测均方差（Mean Square Error， MSE）的均值和标准差分布，并显示了卡尔曼增益矩阵K和协方差矩阵P的二范数随超参数的变化情况，折线表示均值，误差带表示标准差。由于测试函数部分值接近0，计算MSE 时未使用相对值。

图3 超参数选取对数据同化效果的影响Fig.3 Effects of hyperparameters on data assimilation

从图3 可以看出3 种超参数设置对预测结果的影响，全局MSE 与观测点MSE 随超参数变化趋势相同，当观测点基本覆盖了整个定义域时，观测点的预测效果基本可以代表全局的预测效果。

图3（a）显示样本数量越小，预测效果的标准差越大，即预测结果的随机性越明显，当样本数量＞50 时，预测效果的标准差随样本数量的变化已经不明显，但应注意，本测试函数只包含4 个可调系数，样本数量应该随系数数量适当调整；样本数越多，||K||2越接近于1，其标准差也越小，||P||2均值基本保持不变，标准差逐渐减小，卡尔曼滤波矩阵K表征观测值的权重，当样本数增加，权重比例基本保持不变。

图3 （b）表明参数浮动范围δ过小会导致预测的误差增大，此时模型预测结果的||P||2的数值过小，由式（7）可知，||K||2主要受噪声矩阵R影响，也会较小，滤波过程中观测值修正量权重降低，输出结果更偏向模型预测值，预测结果不能得到有效校正；当参数浮动范围δ过大时，预测结果的MSE 增大，会导致数据同化结果不稳定，对于本算例中的非线性测试函数，参数范围的过大调整会导致模型函数完全偏离真实结果。

图3（c）显示过大或者过小的给定观测噪声都会造成预测误差和随机性增加，噪声的给定与样本协方差矩阵无关，故右图没有给出||P||2；当噪声过小时，||K||2数值较大，观测值权重大，但由于模型本身预测能力有限，会导致预测效果失真，当噪声过大时，||K||2显著减小，导致观测结果对模型修正不足，本算例中观测结果没有添加额外噪声，此处的观测噪声主要代表模型与真实函数之间的差异，故给定噪声时应该充分考虑模型的预测能力，即模型与真实过程的偏差，而不仅仅是测量的不确定性。

超参数的给定本身具有一定的经验性，对于复杂问题，受计算量限制，一般难以先进行一遍超参数选取效果的研究，故很难选取到超参数的最优值，但根据以上论述，经过适当调整，一般可以获得一组较优的超参数。

2 研究对象及数值方法

2.1 研究对象

本文研究对象为中等负荷的可控扩散扩压叶型MAN GHH［28］，具体参数如表2 所示，叶栅参数示意如图4 所示。

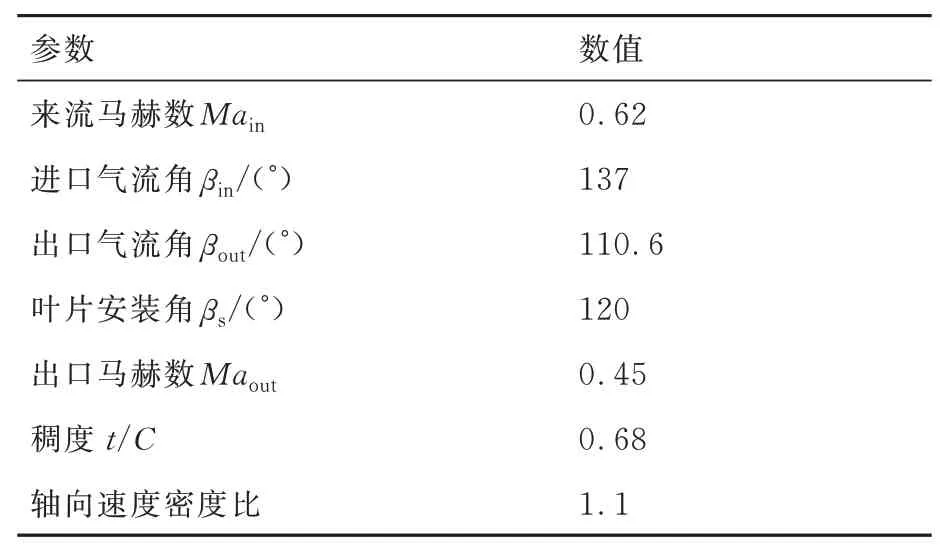
表2 叶型设计参数Table 2 Design parameters of cascade

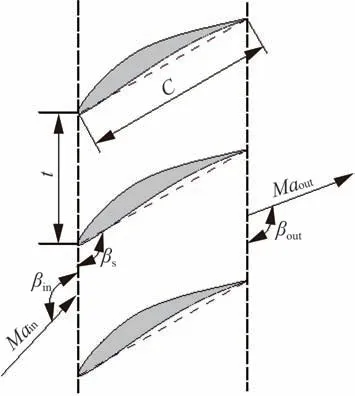
图4 叶栅几何构型Fig.4 Geometry of cascade

2.2 数值方法

为减小计算量，计算过程中使用二维几何模型，网格结构为O4H，网格总数约为7 万，壁面第1 层网格y+约为1，网格划分如图5 所示，经验证满足网格无关性要求。流场数值计算使用ANSYS Fluent，采用有限体积法，重构格式为二阶迎风，计算格式为SIMPLEC 格式。计算过程中固定进口总压，通过用户自定义函数进行二次开发，自动反馈调节出口静压，以获得指定来流马赫数。

图5 网格划分Fig.5 Illustration of mesh

2.3 湍流模型

在航空航天领域，最常使用的湍流模型为SA 模型［29］和SST 模型［30］，为测试不同湍流模型数据同化的效果并对预测结果相互验证，采用这2 种湍流模型分别进行计算。湍流模型的具体方程在此不进行赘述，仅列出2 种模型进行校正的参数名称和默认值，见表3 和表4，参数的具体含义参见文献［29-30］。

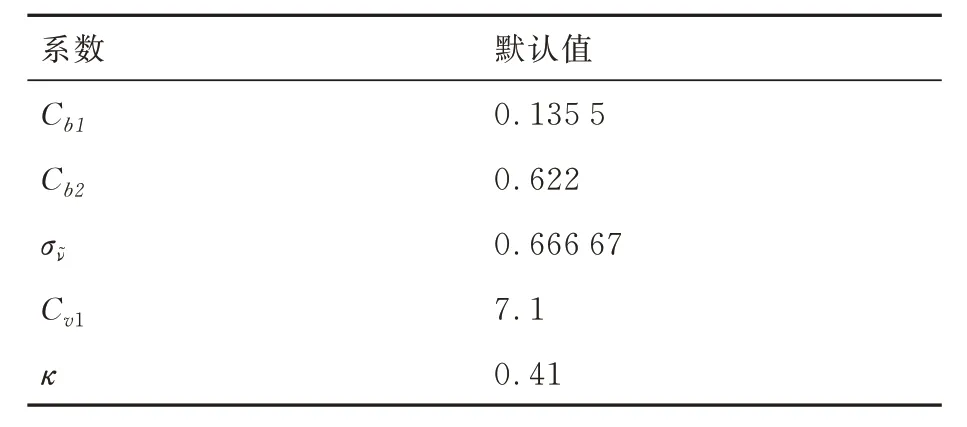
表3 S-A 湍流模型系数默认值Table 3 Default parameters of S-A models

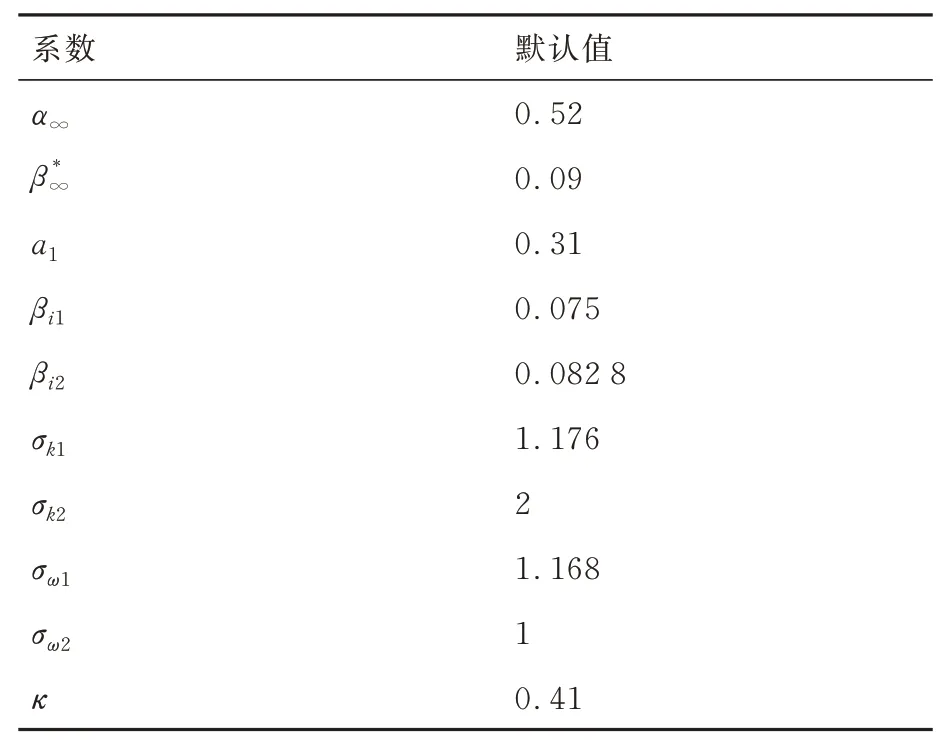
表4 SST 湍流模型系数默认值Table 4 Default parameters of SST models

2.4 数据同化参数设置

考虑到叶栅风洞壁面效应可能会导致流场实际来流条件与标称的工况值有一定差别，来流攻角和马赫数也纳入到校正系数内。边界条件对流场影响显著，单步校正效果有限，为了确保数据同化效果并考虑到湍流模型与边界条件参数在数据同化过程中存在耦合，不同于以往文献［24-25］的单步数据同化，在本文算法实施的过程中，分2 步进行：① 以工况标称的来流攻角α0和来流马赫数Main，0作为初值，初步校正流场的入口边界条件；② 以默认湍流模型参数θt，0和第1 步的结果α1和Main，1作为初值，校正湍流模型参数和来流边界条件，获得新的模型系数θnew，并以此计算新的流场。两步EnKF 数据同化的过程如图6 所示。

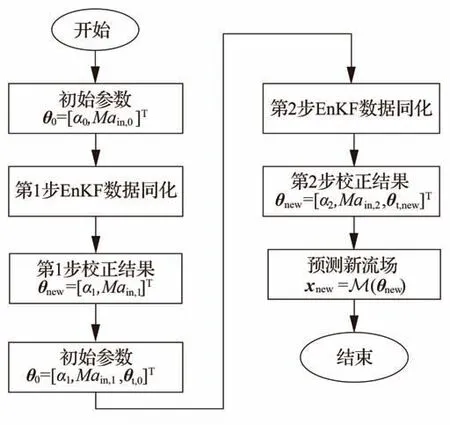
图6 2 步数据同化流程图Fig.6 Flowchart of two-step data assimilation

超参数的给定参照了1.2 节的结果及文献［24-25］，并进行了试算。考虑到第1 步仅校正2 个参数，第1 步数据同化集合样本数目取32，第2步根据湍流模型参数数目，综合考虑计算稳定性和计算量，S-A 湍流模型样本数目设置为150，SST 模型集合样本数目设置为200。参数浮动范围为7.5%，系统噪声为零均值高斯噪声，标准差为0.01。在设计马赫数（0.62）下，对4 种攻角（-4°、0°、4°、5°）共4 种工况进行了数据同化研究。

3 结果与分析

3.1 数据同化结果

数据同化结果如图7、表5 和图8 所示。图7显示了2 种湍流模型数据同化过程中预测结果的相对误差，其中第0 步为初始默认参数的计算结果。可以看出，经过2 步校正后，2 种湍流模型的预测相对误差都有大幅下降：S-A 模型平均降低69.6%，SST 模型平均下降67.0%。但全过程中，SST 模型的预测误差略高于S-A 模型，且第1 步校正误差下降并不明显。表5 显示了2 种湍流模型在数据同化后的来流边界条件参数。可以看出，所有工况的校正马赫数都大于工况标称马赫数（0.62），校正后都在马赫数0.64 附近浮动，不同工况略有差别，但同一工况，2 种湍流模型的校正结果非常接近，最大偏差不超过0.002。攻角也有类似结果，除4°攻角外，其他工况校正攻角与工况的标称攻角偏差均＜1°；但4°攻角工况，偏差超过了1.5°。一般的平面叶栅试验过程中，攻角并非直接测量得到，而是通过转动安装叶栅的转盘到特定的角度获得指定攻角，但在风洞中来流会受到风洞壁面和叶片影响，并非完全平直流动，需要进行进口流场品质调控［31-32］，故攻角的不确性度主要取决于进口气流角的调控效果，一般来说给定攻角和实际攻角都会有一定差别。推测4°工况在试验过程存在一些偶然因素，导致该工况攻角偏差远大于其他工况。对于同一工况，2 种湍流模型结果非常接近，最大偏差约为0.185°。2 种湍流模型结果进行的相互验证可以进一步表明数据同化算法的可靠性。

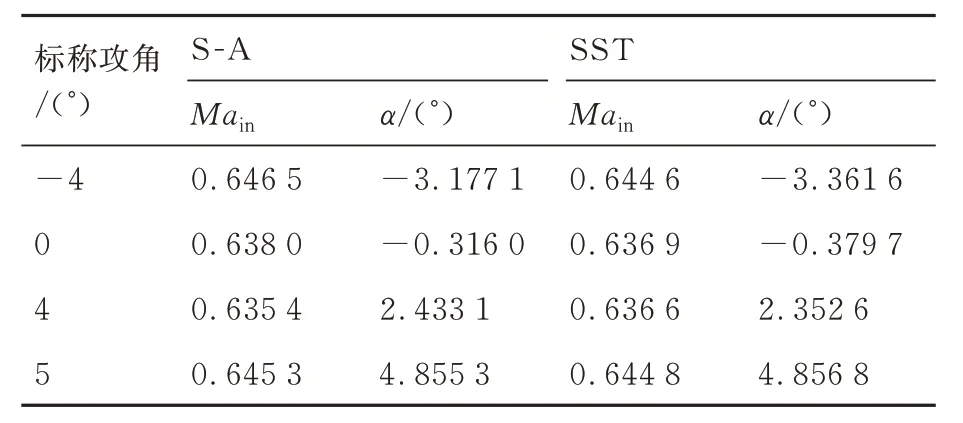
表5 数据同化校正后的来流边界条件Table 5 Coming boundary conditions corrected by data assimilation

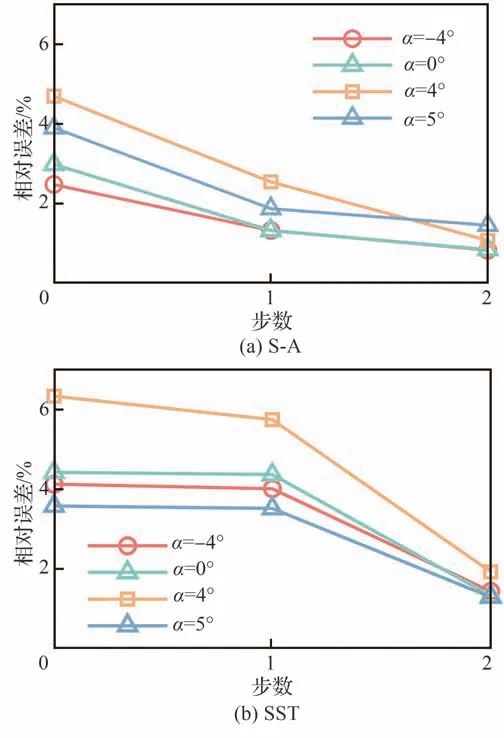
图7 数据同化过程中预测结果的相对误差Fig.7 Relative errors of prediction during data assimilation

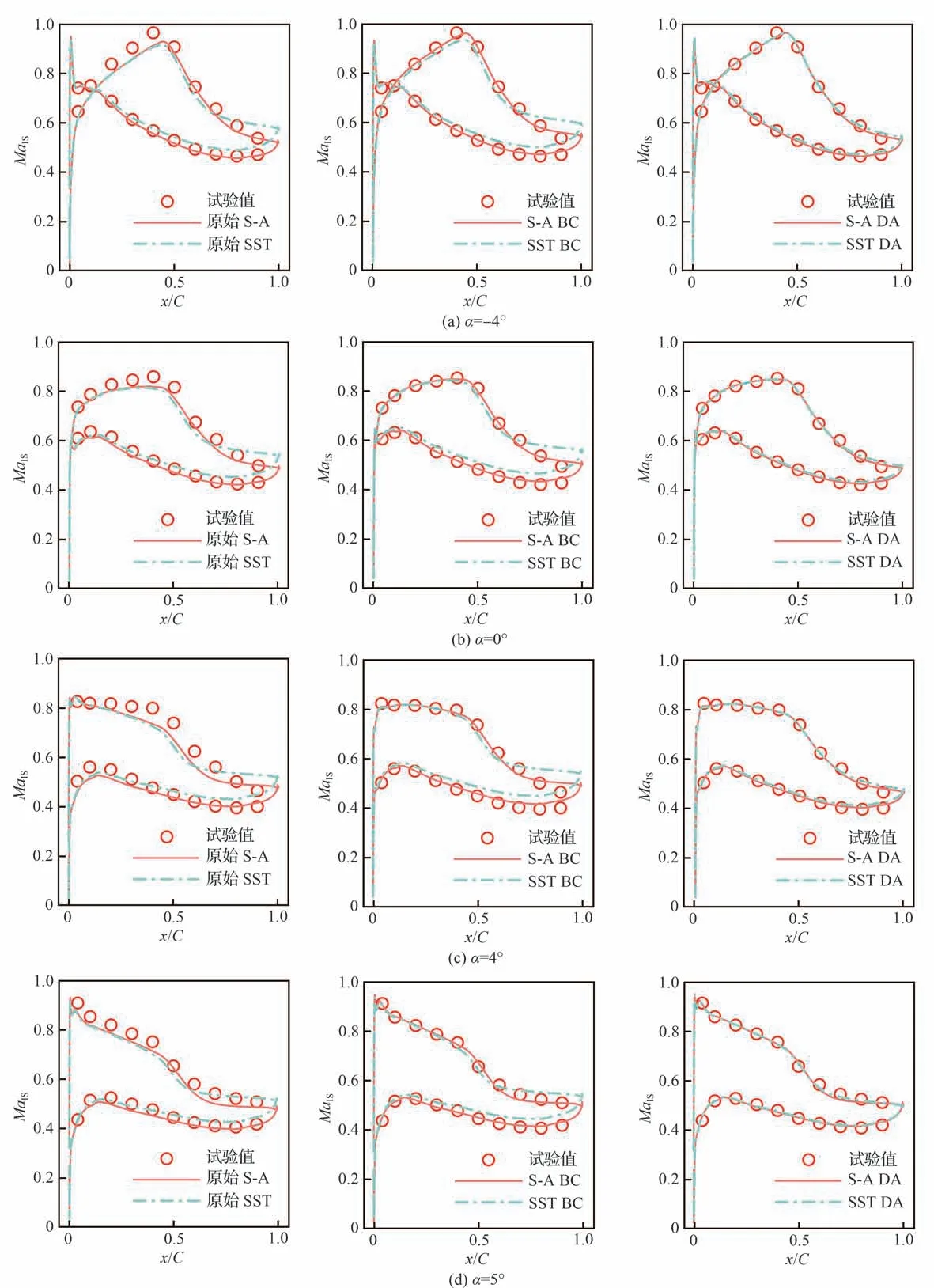
图8 叶片等熵马赫数分布（BC 为仅校正边界条件的预测， DA 为数据同化后校正所有参数的预测）Fig.8 Distribution of isentropic Mach number of blade（BC represents predictions with corrected boundary conditions and DA represents predictions with all parameters corrected by data assimilation）

虽然在本文中应用的算例工况均为中等负荷叶栅的设计马赫数，但本文发展的基于数据同化的试验数据驱动的叶栅流场预测方法对各种负荷的压气机叶栅流场及除堵塞工况外的各工况均可以适用。因为当流动堵塞时，入口马赫数保持不变，无法再通过调整入口马赫数来校正流场的边界条件。

图8 给出了4 种工况叶片表面等熵马赫数的分布情况。左列为完全使用默认参数与试验的对比度，预测结果和试验结果趋势上总体相符，但在吸力面试验值明显高于预测值，而压力面数值上比较相近。为了分别显示来流边界条件参数和湍流模型系数的作用，中间列显示了仅校正了来流边界条件（Boundary Condition，BC）与试验的对比结果，可以看出前50%弦长区域，预测效果明显改善但是叶片尾缘区域的预测效果几乎没有改变，这是由于叶片尾缘存在流动分离，仅修正边界条件不能提高分离预测准确度，SST模型预测的叶片尾缘等熵马赫数明显高于试验结果且偏差要大于S-A 模型。右列显示了完整参数校正后的预测结果，可以看出预测出的等熵马赫数分布与试验测量结果几乎完全吻合，这说明湍流模型参数的校正显著提高了尾缘分离区的预测效果。

另一方面，图8 可以解释SST 模型第一步校正时，误差下降很小的原因。来流边界条件校正主要提高了叶片前半部分的预测效果，但原始参数的SST 模型尾缘等熵马赫数本身存在较大的过预测，在校正来流条件时会使尾缘区域的过度预测更为明显，为降低总体误差，边界条件调整幅值较小，即湍流模型系数与边界条件参数在校正过程中存在耦合，导致SST 模型单纯校正边界条件效果不佳。而S-A 模型尾缘的预测偏差较小，对边界条件校正影响小，即二者耦合程度低，故仅校正边界条件预测误差就有明显减小。

表6 和表7 分别给出了2 种湍流模型各工况校正后的系数，括号中的百分数表示相对默认值变化的百分比。可以看出部分系数有明显的趋势性变化，总体上相对默认值有明显的增大或者减小，如S-A 模型的Cb1、σv，SST 模型的、a1、σk1、σω2、κ等。文献［17-18］为提高S-A 模型对分离流的预测能力，建议增大Cb1参数，文献［26］建议将SST 模型中的参数a1设置为1.0以提高分离流和逆压力梯度流动的预测能力。在调整方向上相关文献与本研究校正结果相符，但由于本研究同时校正了多个参数，而上述文献仅调整了一个参数，故数值上差别较大。部分参数如：S-A 模型Cb2、κ，SST 模型βi2、σω1变化幅度较小，其他参数变化幅度有明显的工况相关性。值得注意的是，2 种模型中都有von Kármán 常数κ，但变化规律明显不同，在S-A模型中基本保持不变而在SST 模型中有明显的增加，原因在于2 种模型对该常数的使用不同。

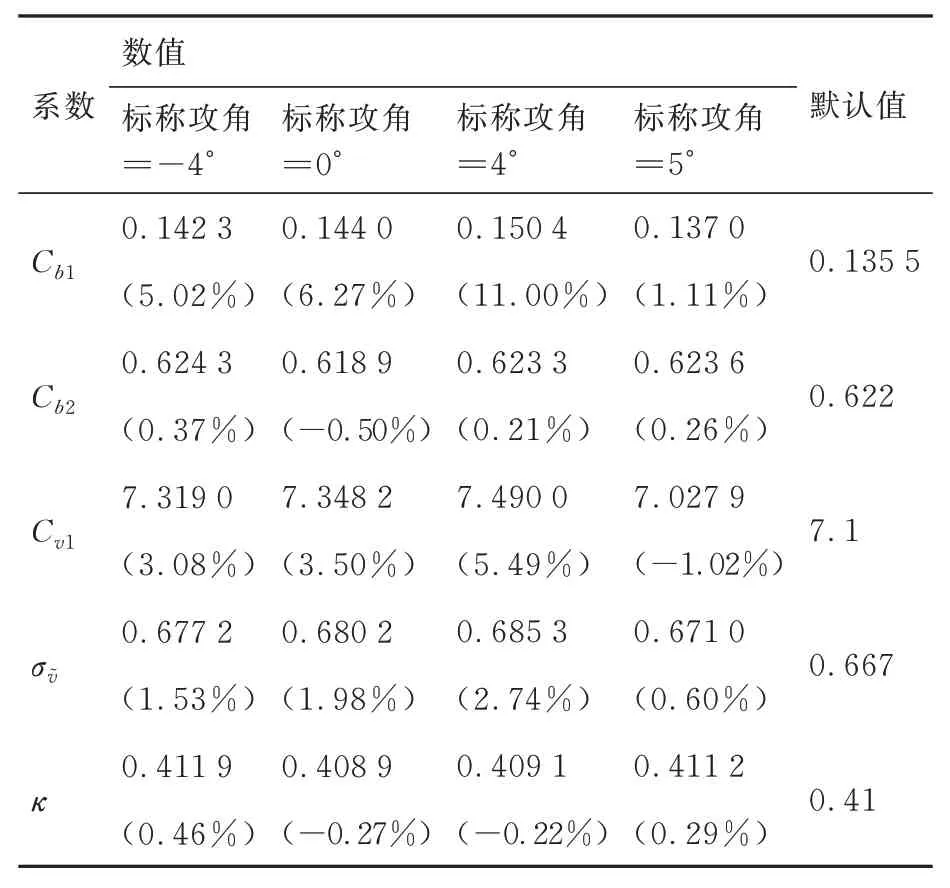
表6 S-A 湍流模型校正系数Table 6 Corrected coefficients of S-A model

表7 SST 湍流模型校正系数Table 7 Corrected coefficients of SST model

校准后湍流模型参数可以有效减小湍流模型对流动分离的过度预测，虽然在其他叶栅上的效果仍有待测试，但由于参数调整幅度不大，参数的调整并不会带来明显负面效果，当其他压气机叶栅流场存在分离区过度预测时，可以参照本文中近似工况的校准参数进行设置以降低分离区过度预测，提高预测精度。

3.2 流场分析

图9 显示了2 种湍流模型在0°和5°攻角预测结果的马赫数云图和流线图，左列为仅校正边界条件的预测结果，右列为校正边界条件和湍流模型参数的预测结果。从流线图可以看出，使用默认的湍流参数，吸力面尾缘的分离泡尺寸总体大于校正后的结果；马赫数云图显示，湍流模型校正后的尾迹范围明显比校正前小。2 种湍流模型默认参数条件下，预测分离区尺寸和起始分离位置有明显差别，但数据同化后2 种模型预测结果非常接近。

图9 2 种湍流模型数据同化过程的马赫数云图及流线图Fig.9 Mach contours and streamlines of two models during data assimilation

图9 也解释了图8 等熵马赫数变化的原因：默认参数的湍流模型预测的分离泡过大，导致叶片尾缘流道变窄，该流场为亚声速流场，流速及马赫数增加，静压下降即等熵马赫数增加，大于试验测量结果；参数校正后预测的分离泡尺寸减小，等熵马赫数与试验测量结果更加接近。

为了进一步分析吸力面尾缘分离区起始位置及叶片所受剪切力的情况，图10 显示了4 种工况叶片压力面和吸力面剪切力系数Cf的分布情况。Cf的正方向为流动方向，当Cf为负值时即发生了流动分离。可以看出，S-A 模型参数校正前后，叶片前50%的区域剪切力系数几乎不变，变化主要发生在尾缘区域，分离点附近变化最为明显。而SST 模型系数校正前后，整个叶片表面剪切力系数都有明显变化，吸力面变化幅度大于压力面。2 种模型在校正后都出现了分离起始点推迟，SST 模型推迟更大，分离点预测位置基本一致，在吸力面前约40% 弦长、压力面前20% 弦长，2 种模型校正后剪切力系数预测有一定差异，其余区域基本一致。剪切力系数在数据同化过程中没有被直接校正，而是受到湍流模型系数的影响产生变化，SST 模型参数校正后前缘区域Cf的变化应该是由于SST 模型边界层对模型系数比较敏感。

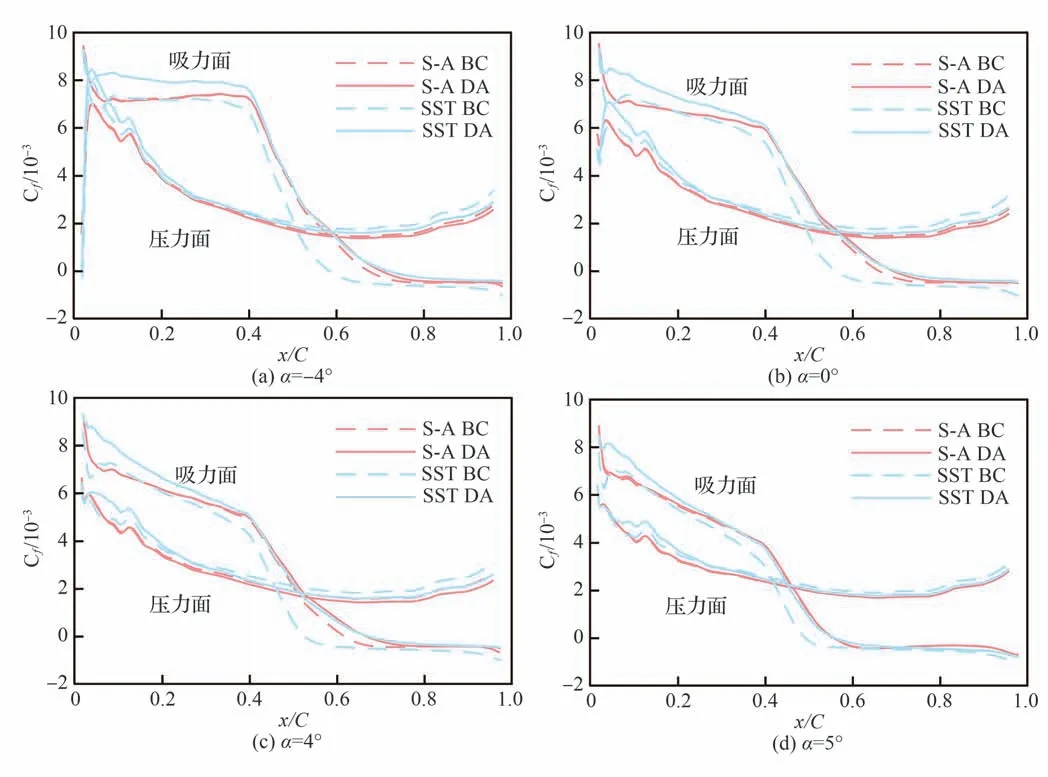
图10 2%～98%弦长区域叶片表面剪切力系数分布Fig.10 Distributions of shear coefficient of blade surface along 2% to 98% chord

本研究使用的试验数据仅来自于叶片表面的静压孔，有必要分析数据同化后叶片下游流动参数的变化情况。图11 和图12 显示了叶片尾缘下游0.34 倍弦长处气流角和总压损失系数ω沿截距方向的分布，xt表示距叶片尾缘的流向距离。可以看出，经数据同化校正后气流角和总压损失系数明显减小，2 种湍流模型预测结果非常接近，叶片尾迹区的位置和参数变化幅值基本一致，尾迹范围小于原始模型预测结果。叶片下游的气流角和损失系数受吸力面分离区影响很大，校正后，分离区尺寸减小，从而降低了气流角和总压损失。

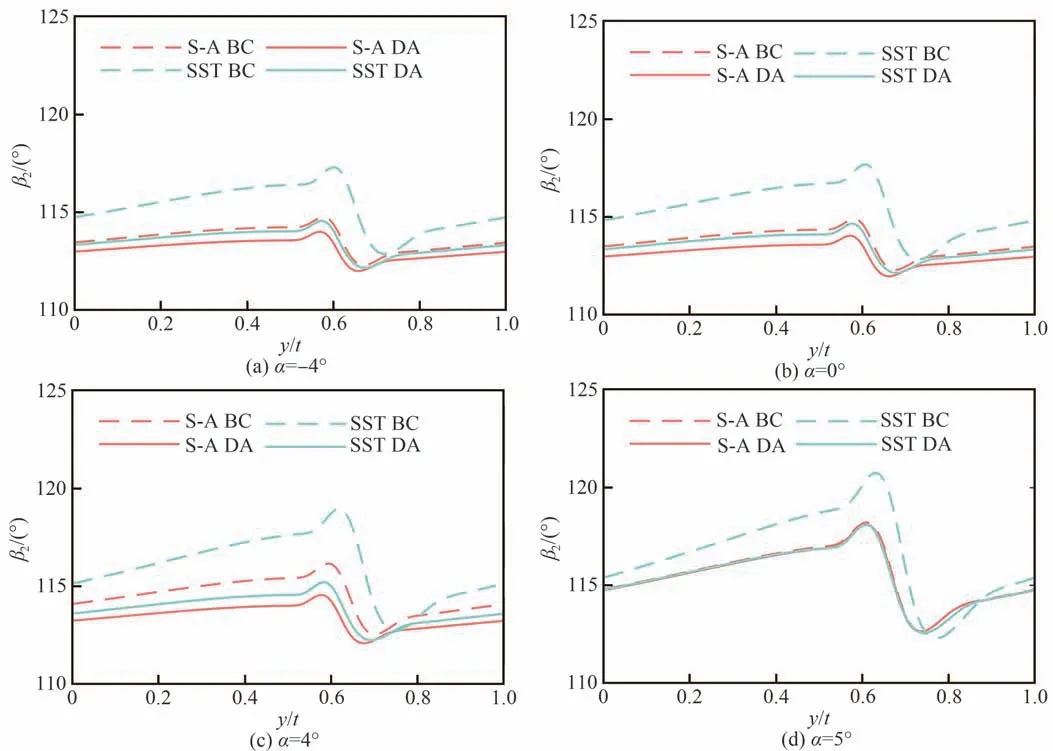
图11 叶片下游气流角（xt/C=0.34）Fig.11 Flow angles at blade downstream （xt/C=0.34）

图12 叶片下游总压损失系数Fig.12 Total pressure loss coefficients at blade downstream

为进一步探究更远处下游流场情况，图13显示了2 种校正后的湍流模型在0°和5°攻角叶片尾缘0.34、1.34、2.34 倍弦长处的总压损失分布情况。可以看出，即便在较远的下游区域，2 种湍流模型预测结果仍然基本一致。这说明使用集合卡尔曼滤波方法对压气机叶栅进行试验数据驱动的流场预测时，全流场中大多数与叶栅性能直接相关的物理量的预测结果对湍流模型依赖性较弱。

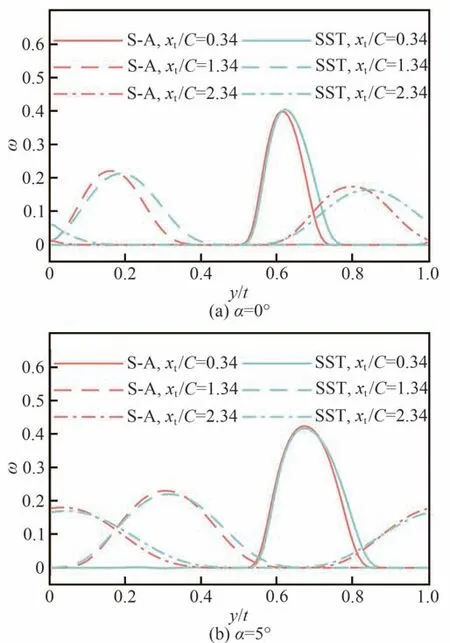
图13 叶片不同下游位置总压损失系数分布Fig.13 Distributions of total pressure loss coefficient at several locations of blade downstream

4 结 论

本文使用集合卡尔曼滤波方法，使用S-A 和SST 这2 种湍流模型对MAN GHH 叶栅进行了试验数据驱动的流场预测。结论如下：

1）使用集合卡尔曼滤波方法进行参数校正时，应该合理选择超参数，其中观测噪声的给定应该同时包含测量不确定度和模型与真实物理过程之间的差异。

2）通过集合卡尔曼滤波的数据同化方法校正湍流模型系数和来流边界条件，可以有效提高压气机叶栅的预测精度，可以使预测误差降低将近70%，由于试验过程中风洞壁面效应的作用，校正来流边界条件是必要的，校正后的湍流模型参数部分呈现一定共同规律性。

3）使用2 种湍流模型分别进行两步数据同化参数校正后，相比原始流场，参数校正后的流场吸力面尾缘分离区尺寸减小，分离起始点延迟，其入口边界条件及流场参数基本相同，即参数校正后的流场对湍流模型依赖性较弱。