主线教学理念下初中数学活动课的实践与思考
仲惟超 柳明
[摘 要]在数学活动课中,学生在活动的引领下,开展自主探究,获得直接经验,提升实践能力。初中数学活动课应以“主线教学”理念为指导,采用“四环节,双主线”的教学策略,从而实现培养学生数学核心素养的目标。
[关键词]主线教学理念;初中数学;活动课
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2023)15-0044-03
一、数学活动课的意义
(一)培养核心素养
数学活动课是指在活动的引领下,学生开展自主探究,获得直接经验和提升实践能力的课程。数学活动课注重引导学生运用数学知识解决实际问题,进一步感悟数学思想方法,积累数学基本活动经验,培养数学核心素养。
(二)实现德育教育
数学活动课以学生为中心,遵循学生的身心发展规律,以正确的价值观为导向,落实立德树人教育目标,促进学生全面发展。
二、初中数学活动课的实施策略
在初中数学活动课中,我校以主线教学理念为指导,实践并总结了“四环节,双主线”的教学策略。“四环节”是指初中数学活动课的呈现、初探、深挖、发散四个环节。“双主线”是指问题线和情感线两条逻辑主线。问题线是指通过设置递进式问题,培养学生的数学素养;情感线是指深挖数学知识的内涵和应用价值,凸显数学魅力,实现德智融合。
本文以人教版教材七年级上册第二章数学活动3“月历中数的规律”为例,通过设置趣味型问题、情境型问题、探究型问题、应用型问题等四种问题,引导学生经历观察、猜想、证明、应用、拓展等过程,从而培养学生的数学思维能力,提升学生的核心素养。同时,将数学规律美在课堂中加以呈现,让学生在数学探究活动中经历感受美、发现美、欣赏美、创造美的过程,彰显数学的美育价值。
三、初中数学活动课的实践案例
(一)内容解析
“月历中数的规律”活动课是第二章“整式的加减”的内容,主要是借助整式的相关知识,引导学生探究和表示月历中数的规律。
本节课围绕月历设置探究活动,拉近了数学和生活的距离;让学生应用数学知识解决实际问题,增强了数学的实用性,培养了学生的数学应用能力和思维能力。
(二)教学目标
(1)能利用整式加减的相关知识探究月历中数的规律,并能借鉴相关方法自主设计探究方案和解决其他规律性问题。
(2)经历探究规律的一般过程,进一步体会用字母表示数的重要意义,培养数学模型思想。
(三)教学重难点
重点:用代数式表示月历中数的规律。
难点:灵活设未知数,让规律的发现过程简洁明了。
(四)教学过程
课前交流出发点:由于本节课的授课时间在秋季,教师拿出在校园内拾取的一片落叶,询问学生能想到什么。
师:同一片落叶,佛学家想到轮回,作家想到哀愁,物理学家想到万有引力,数学家想到形状和大小……可见观察事物的角度不同,对待事物的看法也不同。今天,我们就尝试用数学家的眼光研究身边的事物,看看本节课哪一位同学能成为出色的数学家。
设计意图:在课前交流中通过呈现不同学派对待事物的不同看法,引导学生用数学的眼光观察世界,用数学的思维思考世界。
环节1:设疑激趣,呈现载体
趣味型问题:月历不仅能够告诉我们日期、星期、节日,还能用来变魔术。请同学们在月历上任意圈出连续的三个数字,只要你们告诉老师它们的和,老师就能快地说出这三个数字。
追问1:你们知道这个魔术的原理吗?
追问2:怎样论证这个新发现呢?
设计意图:借助魔术引入,设疑激趣,让学生感受到月历上的数字不是孤立的。通过追问,引导学生从特殊值中发现数字规律,再利用字母的一般性推理总结规律,让学生感受从特殊到一般的归纳思路。
环节2:观察月历,观察规律
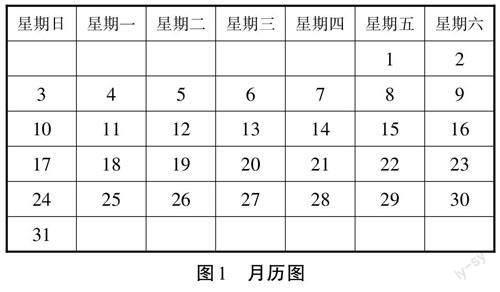
情境型问题1:你们能发现月历(见图1)中的数字有哪些规律吗?
学生独立思考、小组交流后进行展示汇报。从中可以看出,学生的关注点只聚焦在横向数字和纵向数字之间的大小关系,忽略了其他方向上的数字之间的大小关系。对此,教师继续追问。
追问1:月历中斜对角方向上的数有什么规律?
追问2:为什么会产生这些关系?
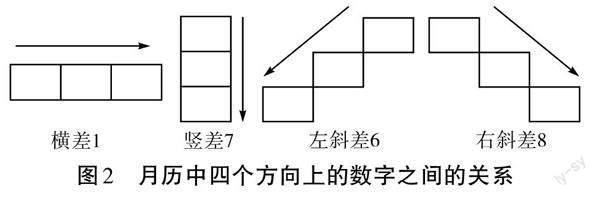
教师引导学生总结月历中四个方向上的数字之间的关系(见图2)。
设计意图:设置开放性强、起点低的情境问题,使学生充分开拓思维,发挥想象,进而培养学生的分类讨论思想,激发学生参与探究的热情。
追问3:根据环节1发现的月历中连续三个数字之间的关系,假如设其中一个数为a,其他两个数能用a表示吗?
课堂巡视发现,大多数学生将第一个数设为a,部分学生将第二个数设为a,极少数学生将第三个数设为a。教师可以引导学生回头望,回忆环节1中的魔术,并思考老师为什么想得那么快,进而发现最优设法。
追问4:我们一起来看横向三个连续的数,你知道环节1的魔术的奥妙了吗?设哪个数为a,能够快速简洁地解释魔术中的数学道理呢?
追问5:你能否用此种设法表示其他几种情况?有何发现?
学生通过设中间一个数为a,快速地发现了规律,教师进行如下板书。
(1)橫向“三连数”:(a-1)+a+(a+1)=3a;
(2)纵向“三连数”:(a-7)+a+(a+7)=3a;
(3)左斜“三连数”:(a-6)+a+(a+6)=3a;
(4)右斜“三连数”:(a-8)+a+(a+8)=3a。
设计意图:通过整式的加减运算,使学生的思维碰撞出火花。从三种不同设法到最优设法的思考,让学生既发现隐藏在月历中数的规律,又经历思维优化过程,完成知识的自主建构,在解决问题的过程中发展符号意识。
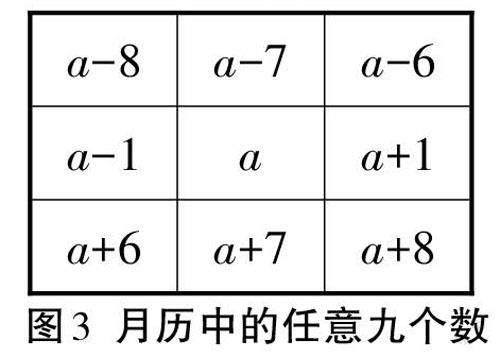
情境型问题2:在月历中任意圈出3×3的正方形方框,若将其中一个数设为a,那么该如何表示其他八个数?这九个数的和与中间数有何关系?
有了上一个活动的经验,学生很容易想到设中间数为a(见图3),并进一步发现这九个数的和与中间数之间的关系。
追问6:根据前面“三连数”和的规律,你能想到用其他方法快速得到这九个数的和与中间数之间的关系吗?
追问7:任意改变正方形方框的位置,结论还成立吗?
设计意图:通过改变方框的大小和位置,让问题层层递进、逐渐深入。以问题引发思考,让“规律美”逐渐得到认同。
环节3:自主设计,深挖规律
探究型问题:观察下面月历中特殊的格子图形(见图4),你能发现并得出什么结论?请尝试结合前面的探究过程和方法,思考完成该问题。
追问8:你能否继续发挥想象,在月历中设计一些图案,并探索图案中数字之间的关系?
学生设计了“H”“X”“回”“十”字形等图形,并思考其中数字之间的关系。
设计意图:通过改变格子图形的形状,让学生进一步体验从特殊到一般的数学归纳思路。同时,在设计格子图形的过程中,引导学生利用所学知识表示规律,体验数学有用、有趣、有美。
环节4:知识迁移,发散规律
应用型问题:图5是一个10×5的数阵,由连续的奇数组成。数阵中的数有什么排列规律?若用平行四边形框出四个数,这四个数的和为120,那么能否知道这四个数?能否框出四个和为180的数,为什么?
设计意图:跳出月历问题,利用本节课中发现的数字规律,将数字规律的探索与应用推广到一般问题中,再次体现从特殊到一般的数学思想。同时,完整地呈现“分析问题—形成理论—解决问题”的活动过程,能让学生在解决问题的过程中欣赏自己所发现的数学规律美。
拓展应用:出示杨辉三角、数码相机成片、自然界中的分形图等(见图6、图7和图8),让学生立体感知数学中数字规律的魅力,进而达到升华育人的目的。
四、教学反思
(一)过程与结果的权衡
本节课一共包含三个重要内容:一是利用本章重点知识,用字母表示一般规律,借助整式的加减进行算式的化简,进而呈现月历中数的规律;二是借助生活实际问题呈现学生在初中阶段所接触的数学思想方法;三是让学生体会从特殊到一般的数学思想方法,并在用字母表示数、发现数的规律的过程中感受数学规律的一般性。第一个内容学生已经在章节前进行了细致的学习,本节课主要以“月历”这一生活中常见的事物为素材,创设问题情境进行知识的巩固与应用。第二个内容和第三个内容属于数学思想方法层面,七年级学生对“数学思想方法”的认识还处于浅层,和教学目标的达成还有很大的距离。初中数学的思想方法必然經历从模糊到清晰的形成过程,这需要给予学生时间和空间上的保障,只有让学生充分体验数学学习过程,才能让他们悟出数学知识中蕴含的数学思想方法。因此,在数学活动课中,获取规律性的结论固然重要,但让学生经历探究、创造、思考、交流的过程,体会从特殊到一般的数学思想方法更为重要。
(二)知识与思想的碰撞
数学知识的学习是数学课堂教学的重要组成部分,但不是全部。本节课的导入环节,有的教师专注于为本节课的问题解决打好知识基础,设置复习旧知环节。这样虽然可以很好地唤醒学生对知识的记忆,但让数学活动课缺少了应有的吸引力和氛围,学生的数学思维也被压制而非唤醒。本节课的教学设计中,从课前交流环节用数学的眼光看待一片树叶,再到环节1的魔术猜数,目的都是激发学生的学习兴趣,使学生在学习知识时数学思维被唤醒,同时感受从特殊到一般的归纳思路,实现了知识与思想的碰撞。
(三)教学与德育的融合
我们一直倡导学科教学与德育融合,数学活动课恰好给数学学科教学与德育的融合提供了很好的路径。德育与常规的知识教学不同,不能传授只能渗透,而渗透的过程需要环境,数学课堂中的“环境”往往是数学活动,也可以是精心设计好的问题。本节课以月历为活动载体,通过设置趣味型问题、情境型问题、探究型问题、应用型问题,让数学特有的规律美得以被学生感受、发现、欣赏和创造,使学生在潜移默化中接受德育教育,实现数学学科的育人价值。
[ 参 考 文 献 ]
[1] 毛桂芸.递进式数学活动课教学实例:“月历中的数学”[J].中小学数学(初中版),2020(Z2):60-61.
[2] 伍晓焰.初中数学活动课的教学实践与思考:以“日历中的规律”为例[J].中学数学研究(华南师范大学版),2021(6):22-24,50.
(责任编辑 黄春香)

