基于IKGC-PSO算法的无人机三维路径规划系统
于力涵,洪 儒,吴宇伦,谢迎娟
(河海大学 信息科学与工程学院,江苏 常州 213002)
0 引言
无人机是无人驾驶飞行器的统称,由于其便利性,广泛应用于农业、电力行业、军工业等领域[1-5]。在无人机领域研究中,路径规划对于无人机执行飞行任务时规避障碍至关重要[6-7]。
在实际应用中,无人机面对的是较为复杂的环境,也需要综合飞行角度、飞行高度、燃料损耗、障碍物阻挡等限制条件。为此,高效精准的路径规划算法是无人机安全稳定执行任务的关键[8]。
在三维问题中,传统算法Voronoi[9]、人工势场法[10]等由于自身的缺陷,存在耗时长,过程繁杂,精度低等缺陷。为了尽量规避传统算法的不足,在现如今研究中,受自然界生物运动启发的智能算法由于其在处理离散变量、非连续性问题的优越性[11]和面对复杂环境的强寻优能力,越来越多地投入无人机路径规划研究中。
文献[12]考虑种群个体与环境因素,在二维环境中利用改进粒子群算法,在例子迭代更新过程中,引入自适应因子,提高了整体搜索能力,但仿真环境局限于二维中,实际应用意义较低。文献[13]对灰狼算法做出改进,融入Powell算法,对原始灰狼算法的全局搜索能力和局部搜索能力作出兼顾,通过仿真分析,提高了路径寻优的精度,但在无人机物理实验上缺乏有效的实例。文献[14]在飞行路径平滑处理上引入了三次B样条插值处理的方法,在标准粒子群算法中引入遗传算法的变异、交叉等思想,具有较好的鲁棒性,但迭代次数有所增加,优化效果存在一定的损失。文献[15]引入柯西变异,对狮群算法易得出的局部最优解进行扰动,增强全局搜索能力,适用于城市中不同的距离规划,但城市环境模型建立时较为规整,模型的复杂度略显不足。文献[16]利用深度强化学习的方法,使无人机能够进行目标跟踪,但深度学习硬件要求较高,训练量大且十分耗时。文献[17]为了解决粒子群算法易陷入局部收敛的问题,在优化寻解过程中引入了牵引力操作,提高了摆脱局部收敛的能力,但在全局搜索能力的加强上效果有限。
本文设计了无人机三维路径规划系统,模拟了实际的三维环境,在设立山峰的基础上,补充了探测雷达和攻击雷达,使模拟环境更加复杂化。选取了路径总长度、飞行高度差以及马尔科夫生存状态的比例均值来构造目标函数。为了避免标准粒子群算法易陷入局部收敛和标准遗传算法收敛速度较慢的不足,提出了一种基于粒子群算法和遗传算法的,融入K均值精英化和柯西变异的优化算法(IKGC-PSO,improve K-means genetic Cauchy-particle swarm optimization),通过采用K均值聚类算法进行第一轮的精英初始化,将标准粒子群算法的随机初始化里的低品质粒子筛除,留下精英粒子,优化粒子种群的分布,从源头上加强算法的全局搜索能力;接着动态化个体学习因子和社会学习因子,强化惯性权重的全局性,保留粒子群算法收敛速度快这一优点的同时,进一步摆脱局部收敛困境;最后融入遗传算法的分组、选择、交叉、变异环节。在进行变异环节时,采用柯西变异的方法,改善静态变异使最优解不充分的缺陷,最大程度上避免陷入局部收敛,提高收敛速度和精度。在仿真平台上,模拟三维实况图,验证了优化后方法的有效性和鲁棒性。
1 系统设计
本文设计的无人机的三维路径规划系统是一种用于确定无人机航行路径的技术。它基于无人机的起始点、目标点和环境信息,计算出一条安全且有效的路径,使无人机能够避开障碍物、遵守航空规则,并在规定时间内到达目标点。
该系统分为硬件和软件两大类,以下是其主要组成部分:
1)传感器:无人机路径规划系统使用各种传感器来获取环境信息,包括激光雷达、摄像头、超声波传感器等。这些传感器帮助无人机感知其周围的物体和障碍物。
2)地图构建:通过传感器获取的数据,无人机路径规划系统可以构建三维环境地图。这些地图描述了无人机周围的障碍物、地形、建筑物等信息。
3)障碍物检测与避障:路径规划系统会分析地图中的障碍物,并使用障碍物检测算法来识别可能的碰撞风险。系统会根据检测结果生成安全的飞行路径,以避开障碍物。
4)路径生成与优化:基于起始点和目标点,路径规划系统会使用算法生成初步路径。本文采用IKGC-PSO算法。生成的路径经过优化,以最大程度地减少航程、提高效率或满足特定的飞行需求。
5)航空规则遵守:无人机路径规划系统会考虑适用的航空规则和限制条件,例如最低飞行高度、禁飞区域等。系统会确保生成的路径在规定的航空规则范围内。
6)实时控制与执行:路径规划系统将计算出的路径传递给无人机的控制系统,以实现路径的执行。控制系统会根据路径指令控制无人机的姿态和航向,使其沿着规划的路径安全飞行。
系统结构如图1所示。
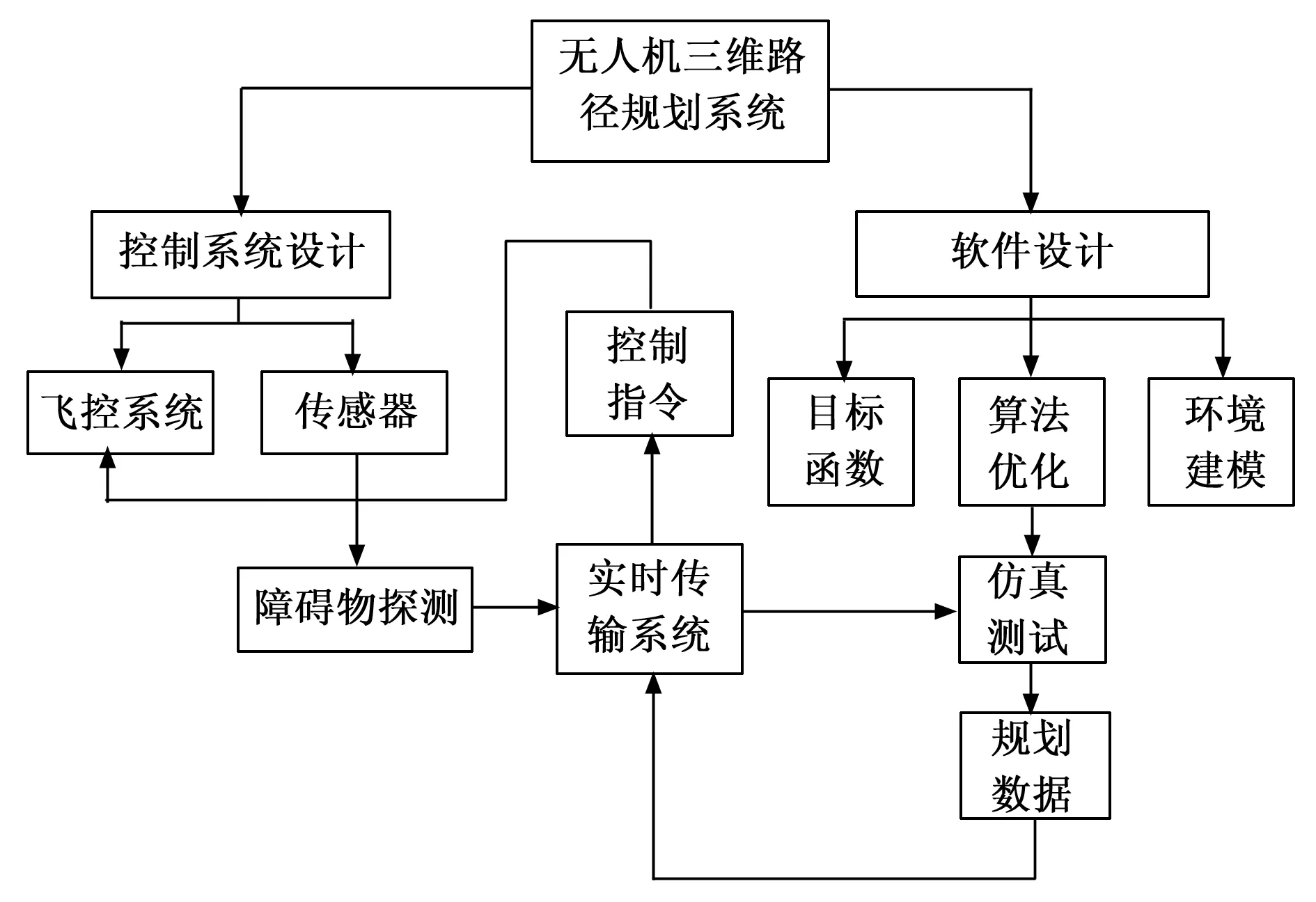
图1 系统结构框图
通过实时传输系统的路径规划数据是无人机执行飞行任务时的核心,下面介绍路径规划数据的生成过程。
2 目标函数
在利用IKGC-PSO算法对无人机三维路径规划的研究中,需要一个评价指标来表示算法效果的优劣,这个评价指标就是目标函数。考虑到实际应用,本文选取了路径总长度、飞行高度差和马尔科夫生存状态三个指标按比例分配构造IKGC-PSO算法的目标函数,其值越低,算法的规划效果越好。
2.1 路径总长度
无人机在飞行过程中,燃油损耗是执行任务时着重考虑的一项指标。易知,越短的路径消耗的燃油量越少。也就是说,无人机飞行路径总长度越短,路径优化程度越好。无人机的飞行路径由n个航行轨迹点组成,每一个航点对应路径规划搜索地图中的一个路径节点[18]。设第i个节点的坐标为(xi,yi,zi),则飞行总距离L为:
(1)
对飞行总距离L引入一个系数λ1,则此部分的目标函数为f1为:
f1=λ1*L
(2)
2.2 飞行高度差
在无人机实际飞行中,稳定的状态有助于硬件系统的简化和硬件资源的高效利用;同时,军用无人机在执行任务时,稳定的飞行状态可以减少暴露风险。为此,对无人机的飞行高度必须有一定的限制。其飞行高度在实际使用中往往有一个范围,本文假设其最低高度为hgmin,最高高度为hgmax,则航行的飞行高度差部分的目标函数f2为:
(3)
式中,λ2为比例系数,hi为第i个节点的飞行高度。
2.3 马尔科夫生存状态
马尔科夫链是一种随机过程,具有马尔科夫性质,其特点是当前状态的概率分布仅依赖于前一个状态,而与过去的状态无关。由一组状态和状态之间的转移概率组成。每个状态之间的转移概率描述了从当前状态转移到下一个状态的可能性。这些转移概率可以用状态转移矩阵或转移概率图来表示。
在军用无人机执行任务过程中,其生存状态即无人机是否正常运行是极为重要的。考虑到无人机航行路线被分割成了一个个节点,且第i+1个节点状态给定第i个节点状态后与其余的节点状态条件独立,具有无记忆性。为此,可以用马尔科夫链模型来抽象出生存状态的目标函数。
设无人机的飞行路径由n个航行轨迹点组成,则第i个时刻的状态可用第i个轨迹点的无人机生存状态来表示。此时无人机的位置坐标设为(xi,yi,zi)。设共有a个探测雷达和b个攻击雷达,第j个探测雷达的探测范围半径为Rsj,第j个攻击雷达的攻击范围半径为Raj,初始状态矩阵为S(i),转移矩阵为T(i),转移损耗系数为α。

C=S(i)+α*T(i)
(4)
当距离大于探测范围半径或攻击范围半径时,马尔科夫生存状态代价C表示为:
C=S(i)
(5)
综上,马尔科夫生存状态目标函数f3如下式:
f3=λ3*C
(6)
式中,λ3为比例系数。
结合路径总长度、飞行高度差和马尔科夫生存状态,本文的目标函数f为:
f=f1+f2+f3
(7)
3 IKGC-PSO算法规划设计
3.1 标准粒子群算法
粒子群算法(PSO,particle swarm optimization)是一种智能启发式优化算法,其模拟鸟群飞行觅食的行为,是一种基于群体的优化方法[19]。粒子群算法是通过个体间的协作和竞争,从而实现对复杂空间中最优解的搜索[20]。
粒子群算法的一个粒子群就是一个搜索域,每一个粒子的信息代表着搜索域中的一个解的情况,其核心参数为粒子的位置和速度。位置向量标识着粒子在搜索域中的位置,速度向量标识着粒子下一步移动的速度和方向。
假定初始粒子种群的数目为n,搜索维度为N,则其位置和速度的迭代更新公式如下:
(8)

标准粒子群算法具有快速收敛的特性,但不可避免地出现过早的局部收敛的现象,使得寻解时往往无法顺利找到全局最优解。
3.2 学习因子和惯性权重初始化
粒子群算法中,学习因子和惯性权重是控制粒子运动过程的两个重要参数。学习因子决定了粒子在搜索过程中的搜索范围,分为个体学习因子c1和社会学习因子c2。这两个常数分别控制粒子向自己的历史最优位置和群体最优位置移动的速度。若简单的使学习因子固定为一个初始值,容易在搜索最优解的过程中陷入局部收敛。为此,在算法的迭代过程中,本文使学习因子动态调整,以达到全局搜索和局部搜索之间的权衡。其式如下:
(9)
(10)
式中,cmin和cmax是固定的上下限值,n为当前迭代次数,N为迭代总次数。在算法的搜索阶段c1>c2,加强了个体粒子寻找路径节点的能力,有利于避免算法陷入局部极小值;在算法的收敛阶段c1 惯性权重是粒子群算法的另一个重要参数,它控制了粒子运动过程中历史速度的影响程度。惯性权重可以看作是粒子保持其历史速度的程度,有助于保持搜索的速度和范围。标准粒子群算法的惯性权重保持不变,在算法的初始阶段,粒子的速度受到惯性权重的影响较大,因此能够更快地搜索解空间;而随着算法的迭代次数的增加,惯性权重会逐渐减小,以使粒子更容易陷入局部最优解。为此,本文对惯性权重做出了如下调整: w=wmax-(wmax-wmin)*exp(1-n/N) (11) 式中,wmin和wmax是固定的上下限值,n为当前迭代次数,N为迭代总次数。惯性权重w随着迭代次数的增加,不断地向上限值逼近,增大了算法迭代后期加速的幅度,尽可能减少了后期陷入局部收敛的情况。 标准粒子群算法的参数动态化跳出局部收敛的能力有限,本文从生成粒子种群的源头考虑,提出了基于K均值聚类的生成初始粒子分布的方法,实现更加均匀的初始分布。其主要思想是将搜索空间划分为多个聚类簇,然后在每个簇内随机生成一定数量的粒子,从而使得生成的粒子更加均匀地分布在搜索空间中,提高算法的搜索精度和效率。 具体地,K均值聚类初始化粒子的步骤如下: 1)随机选取K个样本作为初始聚类中心。 2)对于每个样本,计算它与K个聚类中心之间的距离,将该样本划分到距离最近的聚类中心所在的簇中。 3)更新每个簇的聚类中心,将每个簇内部所有样本的均值作为新的聚类中心。 4)重复步骤2)和步骤3),直到聚类中心不再发生变化或达到最大迭代次数。 5)将K个聚类中心的位置作为粒子的初始位置。 通过K均值聚类初始化粒子的位置,可以使得粒子的初始分布更加均匀,从而提高粒子群算法的收敛速度和聚类效果。需要注意的是,为了避免陷入局部最优解,可以采用多次运行K均值聚类算法并选择其中最优的聚类结果作为粒子的初始位置。 遗传思想是模拟生物遗传进化过程的一种优化方法,它是基于达尔文的进化论,将自然选择、遗传变异、交叉等进化过程应用于算法优化问题中。遗传算法(GA,genetic algorithm)是遗传思想的一种典型实现,由美国计算机科学家 John Holland 在20世纪60年代提出。 遗传算法通过模拟自然选择和遗传进化的过程,实现了从一组随机生成的候选解中寻找最优解的目的。其基本思想是将待优化问题的解表示为一个染色体,并以基因编码的形式存储在染色体中,通过交叉、变异等操作来实现遗传进化过程。 利用目标函数式(7)计算适应度,将每一次迭代的粒子群适应度进行排序,分为N1和N2两个子种群。 对于粒子适应度较好的子种群N1,我们选择直接进行复制操作,将其完整地传递给下一代,以保留其优秀的基因信息。然而,对于适应度较差的种群N2,直接复制可能无法有效地改善整个种群的适应度。因此,我们采用交叉和变异操作来引入新的基因组合和多样性。 交叉操作是通过交换两个个体之间的基因片段,产生新的个体。这样可以将不同个体之间的优势基因组合起来,增加种群的多样性和探索空间,有助于发现更优解。对于适应度较差的种群N2,我们选择进行交叉操作,以期望产生更具优势的后代个体。 另一方面,变异操作是在个体的基因组中引入随机变化,以增加种群的多样性,并有可能发现全局最优解。适应度较差的种群N2也需要进行变异操作,以引入新的基因变化和搜索空间的扩展,希望能够提升其适应度并逐步改进。 通过对适应度较好的子种群N1直接进行复制操作,并对适应度较差的种群N2进行交叉和变异操作,可以实现种群的进化和优化。这样的策略在遗传算法中被广泛应用,以平衡种群的多样性和收敛性,以及加速全局最优解的搜索过程。对粒子i和粒子j进行速度交叉和位置交叉,公式如下: vi(t+1)=a*vi(t)+(1-a)*vj(t) vj(t+1)=(1-a)*vi(t)+a*vj(t) xi(t+1)=b*xi(t)+(1-b)*xj(t) xj(t+1)=(1-b)*xi(t)+b*xj(t) yi(t+1)=c*yi(t)+(1-c)*yj(t) yi(t+1)=(1-c)*yi(t)+c*yj(t) (12) 式中,a,b,c为[0,1]之间的随机值。 柯西变异(Cauchy mutation)是遗传算法中的一种变异操作,它主要用于在搜索过程中引入一定的随机扰动,以增加搜索空间的多样性和避免陷入局部最优解。 柯西变异的原理是利用柯西分布来生成变异后的个体。柯西分布是一种长尾分布,具有较大的方差和极值点,它的概率密度函数可以表示为: (13) 式中,x0表示分布的中心,γ表示分布的尺度参数。 在柯西变异中,对于每一个个体,它都有一定概率以柯西分布为核心发生随机扰动,从而生成一个新的变异后的个体。具体地,柯西变异可以表示为: (14) 柯西变异通过引入柯西分布,使得变异操作具有非线性特性,能够使搜索过程更具探索性和随机性,在搜索空间中产生较大的扰动,更好地探索解空间的各个方向,从而增加发现全局最优解的概率。柯西变异具有一定的探索性,能够在搜索过程中引入一定的随机扰动,增加搜索空间的多样性,防止早熟收敛,避免算法过早陷入局部最优解,保持一定的搜索多样性,有助于全局搜索能力的提升,从而避免陷入局部最优解。 至此,IKGC-PSO的基本框架和优化全部完成,其算法流程如图2所示。 图2 IKGC-PSO算法流程图 IKGC-PSO算法的流程如下: 1)第一轮精英初始化: (1)使用K均值聚类算法对粒子群进行初始化。 (2)筛除标准粒子群算法随机初始化中的低品质粒子,保留精英粒子。 2)动态化个体学习因子和社会学习因子: (1)根据动态化策略,调整个体学习因子和社会学习因子。 (2)加强惯性权重的全局性,保留粒子群算法的快速收敛优点。 3)引入遗传算法的分组、选择、交叉和变异环节: (1)进行分组操作,选择优秀的个体进行繁殖。 (2)通过交叉操作产生新的个体。 (3)使用柯西变异方法改善静态变异导致的不充分问题。 经过一系列的优化,在保证了IKGC-PSO算法寻解搜索速度的同时,尽可能地避免陷入局部最优,提高了搜索的精度。 环境建模可以提供详细的地形信息、建筑物分布和其他地物特征。这些信息可以用于生成无人机的路径规划。路径规划算法可以根据环境建模的数据,选择合适的路径,以最小的代价到达目标点。本次的仿真环境由基准地形和雷达共同组成。基准地形的模型为: (15) 式中,x,y为横纵坐标,z为高度。 雷达模型为: (16) 式中,xc、yc、zc为中心坐标,r为半径矩阵,x、y、z为扩充矩阵,X、Y、Z为雷达矩阵。 在无人机飞行路径的规划中,约束条件用于确保无人机在飞行过程中保持安全,限制无人机避开障碍物、遵循空域规则和限制飞行高度等,从而减少与其他飞行器或地面障碍物的碰撞风险,保障飞行的安全性。进一步合理规划无人机的飞行路径、传输数据量、使用传感器等,以最大程度地利用有限资源,提高任务的效率、成果和飞行的可行状态。本文设立的二个约束条件:速度约束和俯仰角约束。 4.2.1 速度约束 速度约束可以确保无人机在飞行过程中保持适当的速度范围,避免过快或过慢的飞行引发操控困难或飞行失控的风险。通过设定最大速度限制,可以避免无人机超出其可控范围,降低碰撞或意外事故的风险。同时可以帮助优化能量消耗,提高无人机的能量效率。通过合理设置速度上下限,可以避免无人机过度消耗能量或以低效的方式行进,从而延长其续航时间,提高任务执行的效率。公式如下: vmin≤vi≤vmax (17) 式中,vi表示节点i处无人机的速度,vmin和vmax表示无人机的速度上下限值。 4.2.2 俯仰角约束 俯仰角是指无人机机身相对于水平面的前后倾斜角度。通过对俯仰角进行约束,可以控制无人机在飞行过程中的倾斜角度,避免过度倾斜或不稳定的飞行状态。无人机在飞行的过程中会受到环境的影响,改变其垂直方向的俯仰角。当俯仰角偏离到一定程度时,无人机的飞行路径会遭到破坏甚至坠毁。为此,一个合适的俯仰角区间可以确保无人机飞行的稳定性、提高飞行效率和保障飞行安全。约束条件公式如下: θmin≤θi≤θmax (18) 式中,θi为节点i处无人机的飞行俯仰角,θmin和θmax为其飞行俯仰角的上下限值。(xi,yi,zi)、(xi+1,yi+1,zi+1)分别为节点i和节点i+1的坐标。 为了优化无人机的三维路径规划,除了考虑最短路径,还需要确保路径的平滑性和航行的流畅性。在三维路径规划中,当无人机需要转弯时,过于急促的转弯可能导致不必要的摇晃和不稳定,从而影响其性能和安全性。为了解决这个问题,本文引入了三条样条平滑方法进行插值[21]。样条曲线是一种平滑的曲线,通过在给定的数据点之间插值得到。在路径规划中,无人机的路径可以表示为一系列的散点,通过三次样条插值方法,可以在这些散点之间生成平滑的曲线。 为了进一步优化路径的平滑性,对插值后的曲线进行差分处理。差分处理可以计算出曲线在不同点上的斜率,从而获得路径转弯的角度信息。通过确保转弯角度适中,可以使得无人机在转弯时更加平稳,避免急转弯带来的不稳定性。 通过计算三次样条插值得到的散点之间的路径长度,可以评估路径的有效性。路径长度可以作为一个指标来衡量路径规划的质量,较短的路径长度意味着更高的效率和更少的时间消耗。其公式步骤如下: 假设有n+1个数据点(xi,yi)(i=0,1,2…n)。 1)计算每个相邻数据点之间的差值: li=xi+1-xi,i=0,1,...,n-1 (20) 2)计算每个数据点处的一阶导数值(或称为斜率): (21) 3)求解一个三对角线方程组,计算二阶导数值(或称为曲率): (22) pi=3*(di+1-di),i=0,1,...,n-2 (23) 4)求解以下方程组来计算二阶导数值zi,其中z0=zn=0: ai*zi-1+bi*zi+ci*zi+1=pi (24) 5)对于每个数据点,根据二阶导数值zi,构建三次插值函数: (25) 其中:xi≤x≤xi+1,i=0,1,...,n-1。 通过这些步骤,可以构建出一组连续的三次样条插值函数,将给定的数据点连接起来,并且在插值区间内具有较平滑的曲线形状。这些插值函数可用于估计在数据点之间的任意位置的函数值。 仿真平台选用MATLAB R2020a。IKGC-PSO算法的基本参数设置如下:最大迭代次数N=70,种群个数为100个,维度为25。学习因子的下限值取为1.2,上限值取为2;惯性权重的下限值取为0.4,上限值取为0.95;交叉概率取为0.65,俯仰角限制在[-1.8,1.8]之间。环境模型为500 m×500 m×100 m,设置起点坐标为[0.5,0.5,0.4],终点坐标为[49,48,0.6]。 为了验证IKGC-PSO算法的有效性,本文首先选用标准测试函数Griewank函数。Griewank函数的搜索空间为一个n维的超立方体,具有多个较深的碗状结构和一些高度狭长的“山脊”,是一类具有强烈的局部极小值和长而狭窄的最优路径的优化问题。其中,第一项是一个光滑的二次型函数,而第二项是一类高度振荡的函数,对优化算法的性能测试具有较高的挑战性。其具体形式如下: (26) 式中,N为总数,xi为第i个值,当且仅当xi均取0时,函数取最小值,为0。 测试曲线如图3所示。 图3 标准测试曲线 IKGC-PSO算法取得的测试函数的极值为0.008 388,与真正的极小值0相比,误差小于0.01,因此,本算法具有有效性。下面来看具体的理论分析(注意,十米的单位缩写为dam)。 考虑到现实环境十分复杂,本文选用了3个攻击雷达和4个探测雷达作为障碍物,其初始位置如图4、图5所示。 图4 雷达平面图 图5 雷达立体图 接着,将雷达嵌入到复杂的三维地形中,平面图如图6所示。 图6 地形全貌图 为了验证IKGC-PSO算法的有效性和鲁棒性,在攻击雷达和探测雷达数量不变、山峰地形不变的情况下,改变雷达的位置,将其与进行混沌初始化的改进粒子群算法IC-PSO和改进学习因子、惯性权重、融入遗传算法思想的改进粒子群算法IG-PSO进行比对,分别运行了30次并统计了30次搜索解的最优值、最劣值及其方差,结果如表1所示。 表1 算法稳定性对比 由表可知,IC-PSO算法找到的最优解是212.888 9,IG-PSO算法找到的最优解是206.012 4,IKGC-PSO算法找到的最优解是201.365 4;IC-PSO算法找到的最劣解是233.282 9,IG-PSO算法找到的最劣解是226.124 5,IKGC-PSO算法找到的最劣解是204.500 5。较低的最优值表示算法能够找到更接近全局最优解的解决方案,而较高的最劣值表示算法可能会陷入局部最优解或者在优化过程中出现较大的波动。IC-PSO算法的方差是78.566 1,IG-PSO算法的方差是58.986 2,IKGC-PSO算法的方差是1.425 2,相对于IG-PSO算法和IC-PSO算法,IKGC-PSO算法的方差分别减少了97.9%和98.2%,即算法的鲁棒性提高了98%。特别地,IKGC-PSO算法的最劣值仍高于IC-PSO算法和IG-PSO算法的最优值,在无人机三位路径规划上优势极其明显。其优势在于: 1)全局搜索能力:IKGC-PSO算法具有更强的全局搜索能力,能够更好地探索解空间中的潜在最优解。即使在最差情况下,IKGC-PSO算法找到的解决方案仍然比其他算法的最优解更好。这表明IKGC-PSO算法能够克服局部最优解并在解空间中找到更优的全局解。 2)鲁棒性:IKGC-PSO算法对问题的特征和参数设置更具有鲁棒性。它能够适应不同类型的优化问题,并在不同情况下表现出良好的性能。这使得IKGC-PSO算法成为解决各种实际问题的可靠选择。 3)解决方案质量:即使在最差情况下,IKGC-PSO算法找到的解决方案仍然优于其他算法的最优解。这表明IKGC-PSO算法在找到高质量解决方案方面相对更有优势。它可能能够更快地收敛到较好的解决方案,并在解空间中探索更广泛的区域。 4)适应性:IKGC-PSO算法对问题的不同特征和复杂度更具适应性。它具有一定的灵活性,能够在不同的环境中进行调整和优化,以提供更好的性能。这使得IKGC-PSO算法成为处理多样化问题的强大工具。 仿真过程中,目标函数迭代曲线和模拟路径规划如图7、图8所示。 图7 目标函数迭代曲线 图8 模拟路径规划 通过对比观察图6和图7可知,三种算法在收敛效果方面都有较好的表现。IKGC-PSO算法在效果上体现出最为明显的优势。相比之下,IC-PSO算法在迭代的前期和后期表现均一般,寻解效果较差;虽然IG-PSO算法在迭代的前期,寻解能力较强,但迭代3次之后,其搜索能力明显减弱,后期的优化效果不明显。 尽管IKGC-PSO算法在初始迭代时可能稍有不足,但它在寻优水平持续性方面具有明显的优势。在进行了10次迭代后,该算法的目标函数值全面优于其它两种算法;在迭代了48次以后,跳出了局部最优,从全局找到了更优的解,具备足够的寻优能力。其在无人机真实作业场景中发挥重要作用,可以提高无人机的飞行效率、任务完成能力和安全性,能够更好地适应复杂多变的环境,并实现高效、可靠的任务执行。 在对三种算法进行了30次模拟后,数据记录如表2所示。 表2 算法对比 从图7~8以及表2可以看出,在收敛时间接近相同的情况下,IKGC-PSO算法在目标函数平均值方面相较于IG-PSO算法和IC-PSO算法分别减少了5.8%和10.6%,表明IKGC-PSO算法能够找到更优的解,验证了本算法的有效性。 为了解决标准粒子群算法在无人机三维路径规划中存在的局部最优解陷阱、缺乏动态适应性、处理大规模问题困难、路径平滑性差等问题,本文提出了一种基于粒子群算法和遗传算法的,融入K均值精英化和柯西变异的优化算法(IKGC-PSO,improve K-means genetic Cauchy - particle swarm optimization),通过采用K均值聚类算法进行第一轮的精英初始化,剔除标准粒子群算法随机初始化中质量较低的粒子,保留精英粒子,优化粒子群的分布,从根源上增强算法的全局搜索能力。接着,动态化个体学习因子和社会学习因子,加强惯性权重的全局性,既保留了粒子群算法收敛速度快的优点,又进一步摆脱了局部收敛困境。最后,融入遗传算法的分组、选择、交叉和变异环节。在变异环节中,采用柯西变异的方法,改善静态变异带来的最优解不充分的问题,最大程度上避免陷入局部收敛,提高了收敛速度和精度。通过在仿真平台上进行验证,证明了优化后的方法的有效性和鲁棒性。 聚类算法在设置初始化上运用较少,因此,后续将对聚类算法在初始化上的研究进一步展开,更好的优化算法性能,对无人机的路径规划寻求突破。3.3 基于K均值聚类的粒子初始化
3.4 遗传思想优化
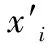
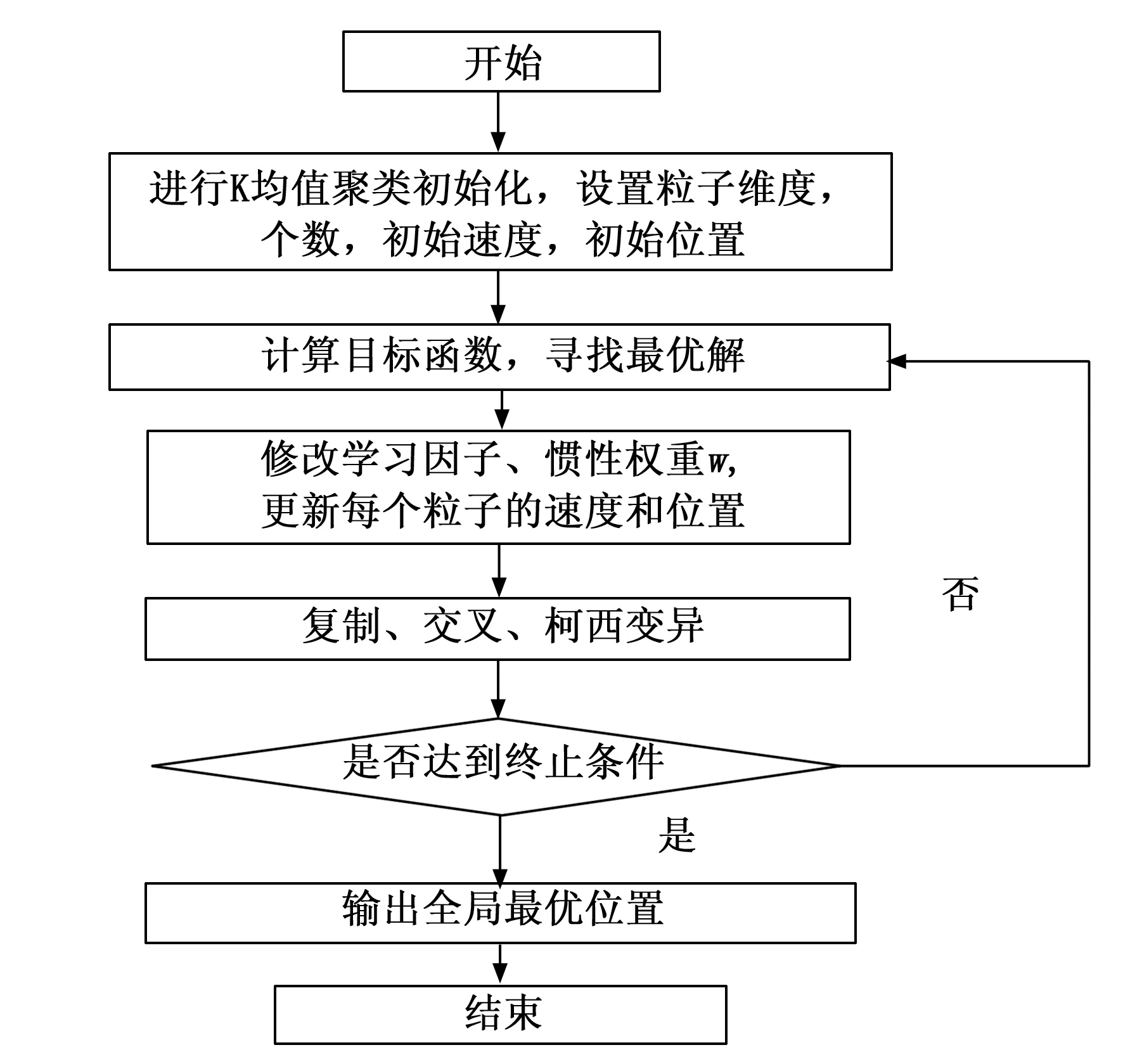
3.5 算法流程
4 环境建模
4.1 三维环境搭建
4.2 约束条件
4.3 路径平滑处理
5 仿真分析
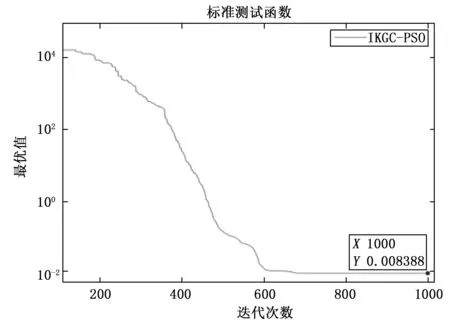
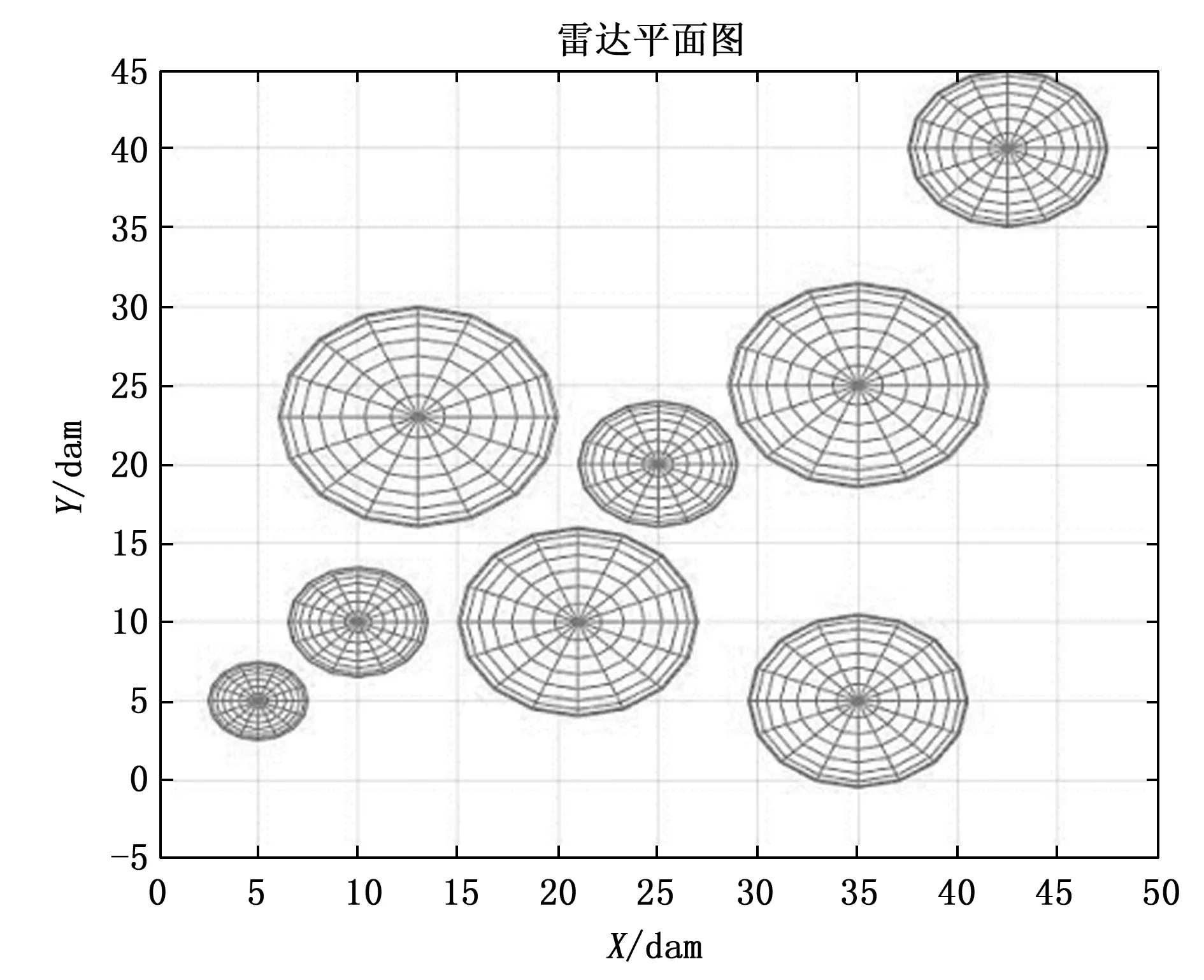
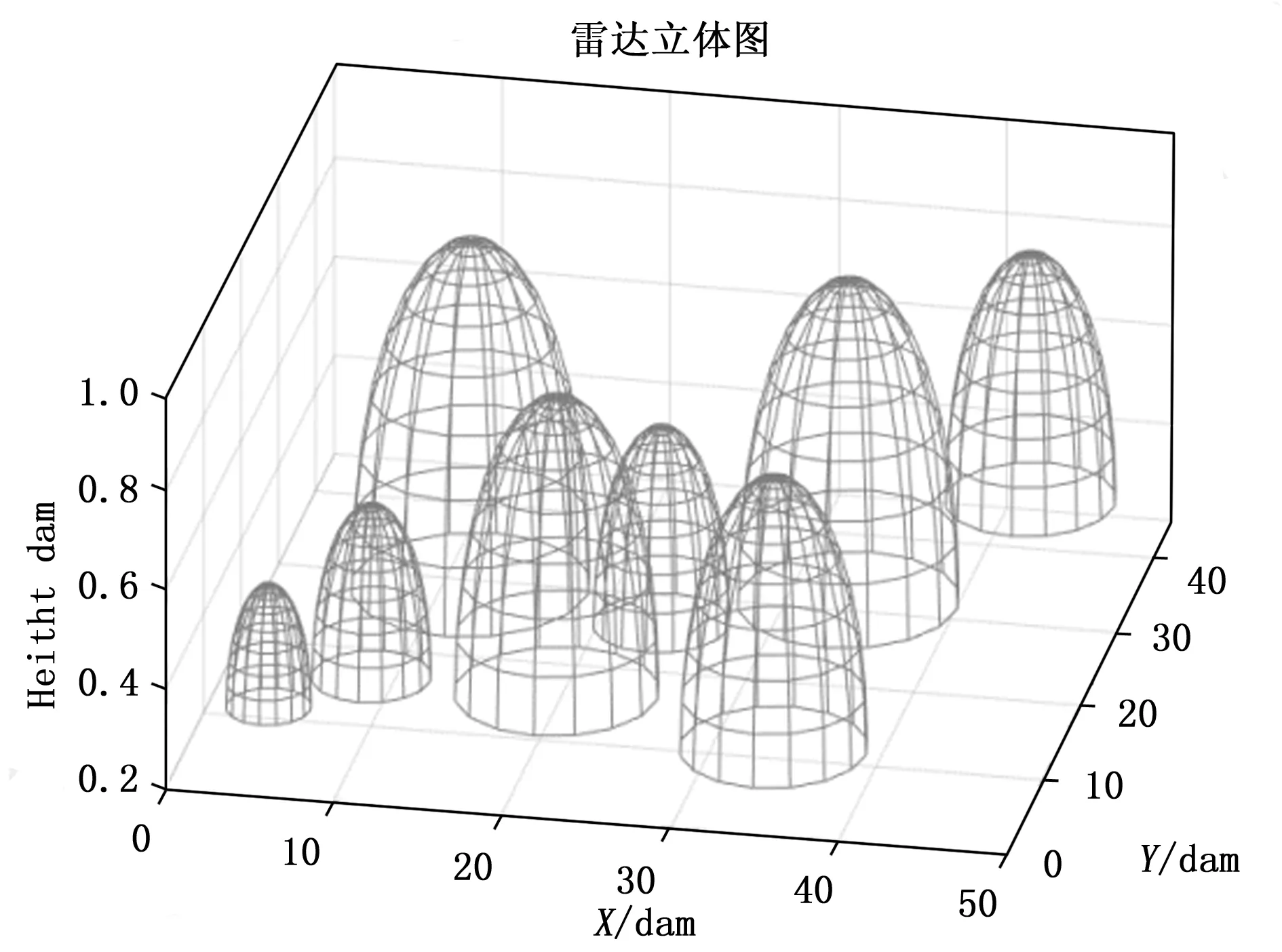
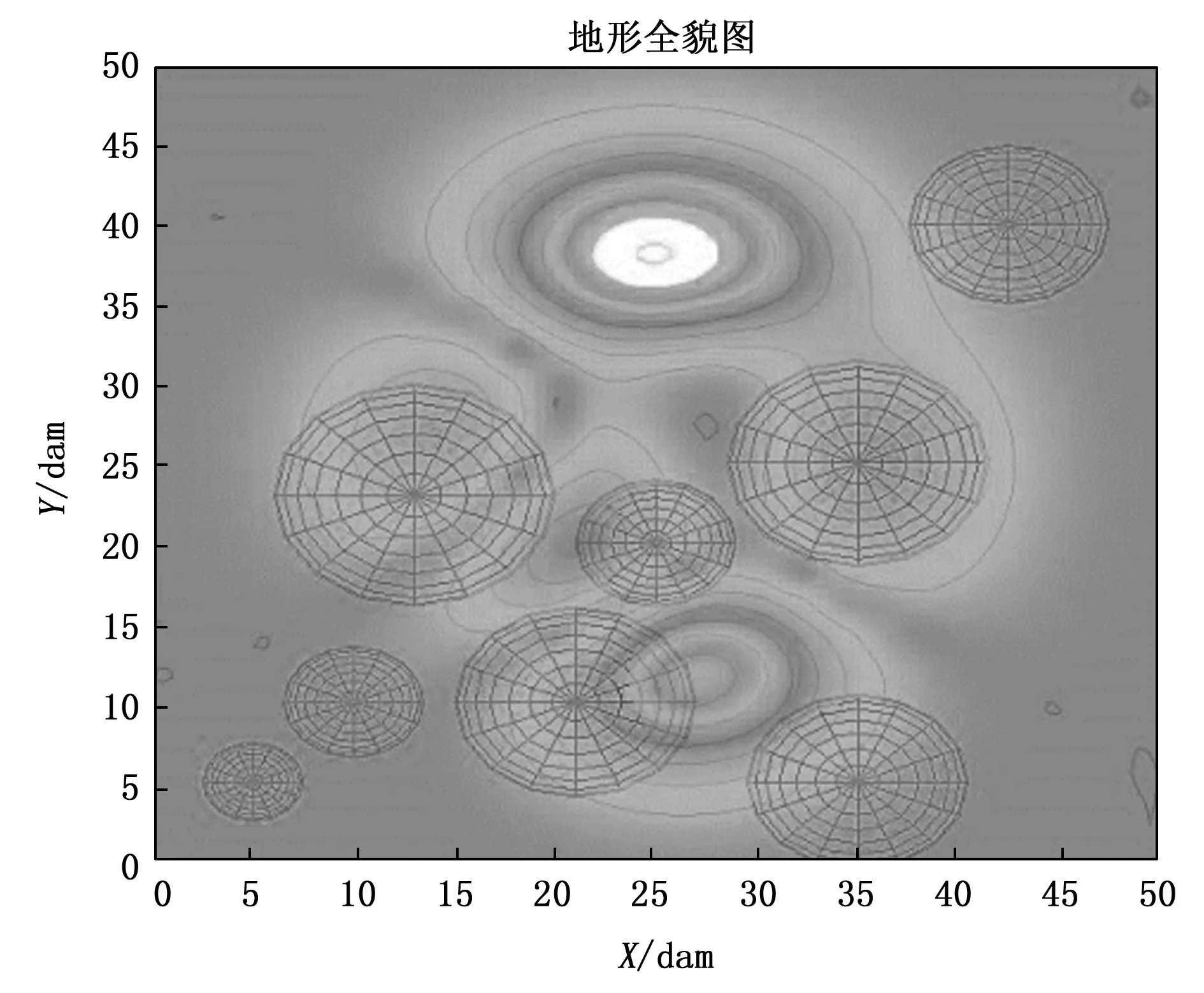
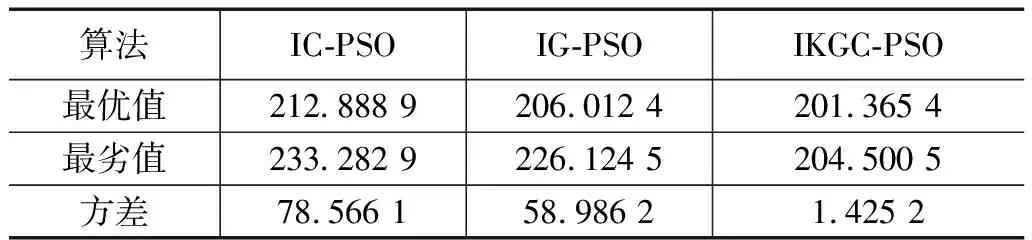
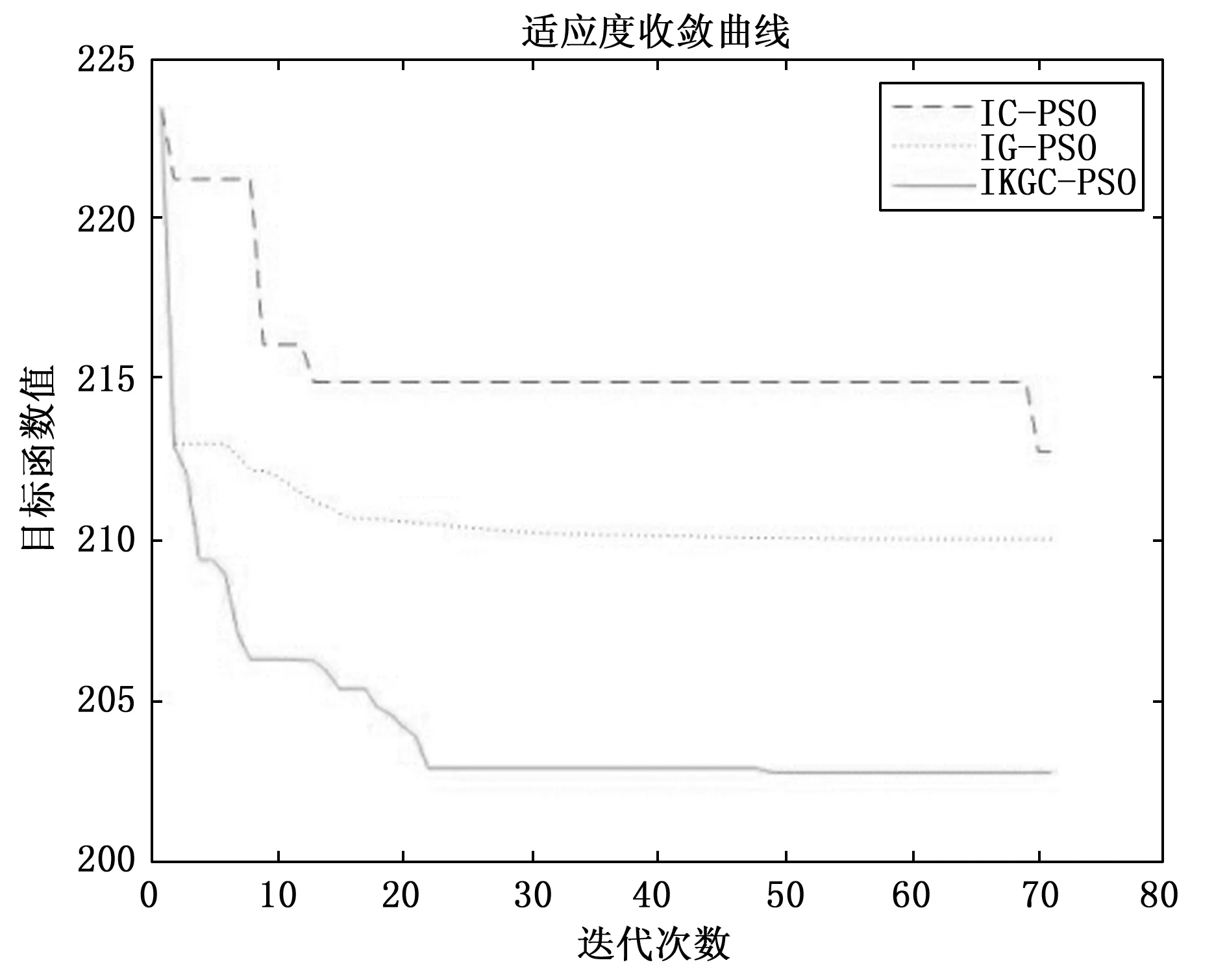
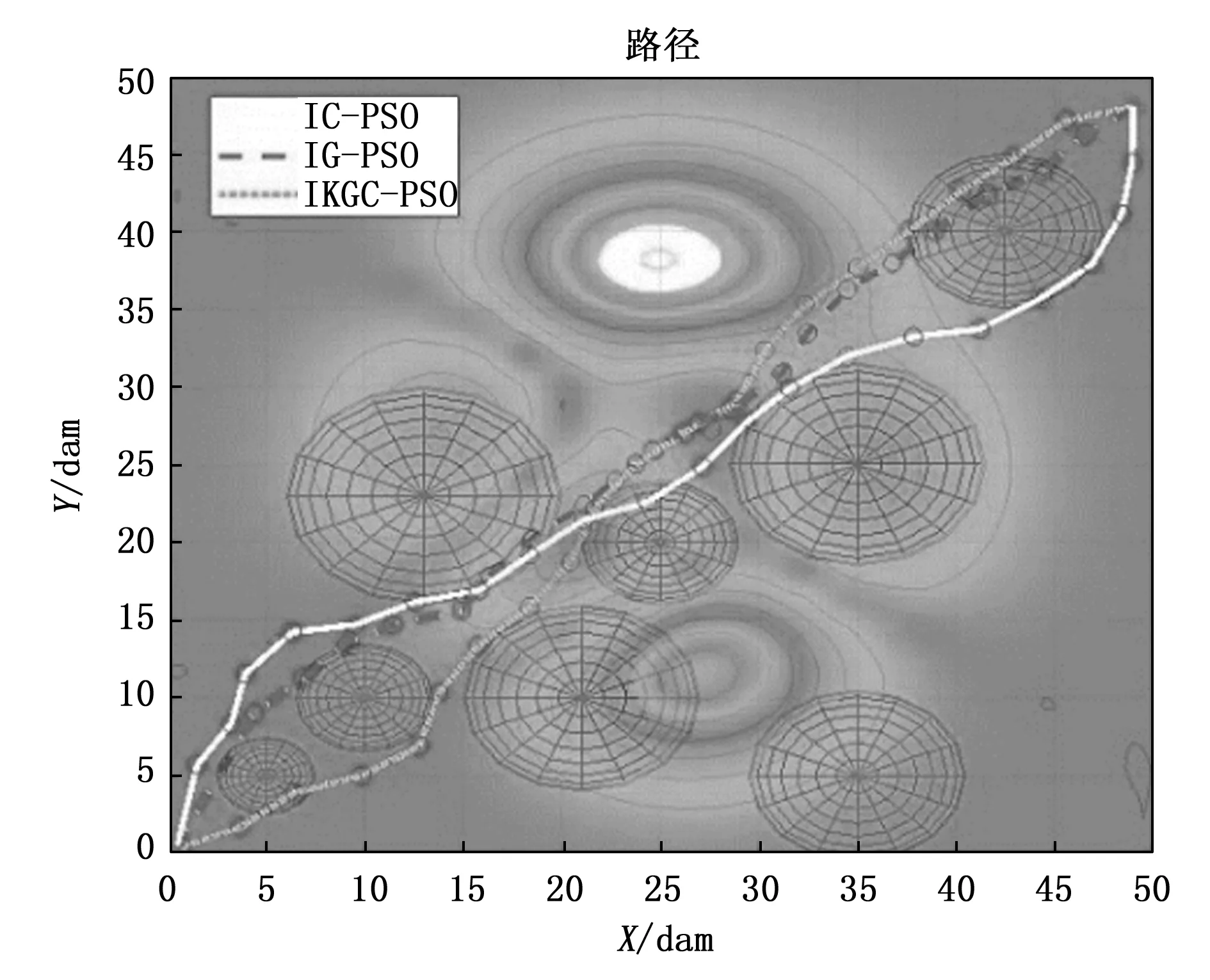

6 结束语

