基于松鼠觅食算法优化LSSVM的泥石流预测

李 璐，张永强，李丽敏，马 媛，窦婉婷，王 悦

(1.西安思源学院 理工学院，西安 710038；2.铜川职业技术学院 机电工程学院，陕西 铜川 727031；3.西安工程大学 电子信息学院，西安 710048；4.西安交通大学城市学院 传播系，西安 710018)

0 引言

泥石流灾害的发生是在自然演变或人为因素的影响下，一种复杂的非线性动力学演化过程。我国山区较多，泥石流灾害是山区常见的一种自然灾害，由于它本身高频发生、分布区域广泛及破坏力极强，对山区人民生命、财产有着极大的威胁，对防灾减灾工作提出严峻的考验。泥石流的早期预报可以有效减少灾害的损失，泥石流形成主要有三大条件，分别是地形地貌、松散物源、水源[1]。近年来国家对地质灾害的防灾减灾比较重视，陆陆续续出台政策，随着灾害的频繁发生，对泥石流灾害的研究一直都是热度较高的课题，相关学者针对泥石流的研究主要有：1)通过灾害区域地面调查结合相关遥感技术，观察并分析泥石流灾害全域的地形地貌，从而分析其成灾机理[2]；2)对物源动储量、泥沙补给、流量等影响因素通过力学及流变学的理论建立相关泥石流的运动方程[3-4]；3)通过实时监测收集雨量信息，对降雨强度与临界雨量阈值分析并建立雨量模型[5]；4)通过实时监测采集成灾因子，对泥石流发生的概率及等级进行预报，从而达到提前预报预警提示，减少灾害重大损失[6]。随着机器学习理论的不断发展，非线性模型也被广泛应用在泥石流灾害预测的理论中，文献[7]融合泥石流的多个影响因子，通过遗传规划法建立临界降雨指数智能预测模型；文献[8]基于PCA(principal component analysis)筛选泥石流灾害成灾因子并使用BP(back propagation)神经网络对泥石流发生的危险性进行预测，此方法选用有效成灾因子的方法结合预测模型极大提升了泥石流危险性的预测，但是使用PCA筛选因子处理非线性关系有一定缺陷。文献[9]使用混合核函数改进了KPCA筛选因子算法，预测等级达到一定的提升。基于这一思想，学者[10-12]将成灾因子筛选、模型参数寻优等优化模型方式使得预测模型精度更加稳健。本文借鉴这一思想分析泥石流全域地形地貌成灾机理并筛选因子，构造出泥石流灾害预测模型。

为进一步提升泥石流预测的精度，本文以陕西省山阳县中村镇泥石流全域为研究对象，首先分析灾害区域地形地貌选出成灾因子，避免因使用单因子预测导致的精度低问题；其次采用核主成分分析法(KPCA，Kernel principal component analysis)进行高维度影响因子的筛选；另外构造最小二乘支持向量机(LSSVM，least squares support vector machines)模型对泥石流发生概率模型的建立，相对于支持向量机将非线性问题转换为线性问题求解方式极大的简化，同时使用多算法进行LSSVM中的超参数优化，经过优化后的模型解决了过早收敛导致陷入局部最优的问题以及参数随机选取导致的精度不佳问题，通过模型优化提高了泥石流预测的精度。最后通过与其他寻优预测算法进行比对，比对出最佳预测模型，为泥石流地质灾害研究带来活力及新思路。

1 算法理论

1.1 KPCA方法

主成分分析方法[13]是一种无监督降维算法，针对线性数据效果较好，但是其对于数据之间存在非线性关系时PCA降维效果比较差，为了弥补这一缺陷，在PCA计算协方差矩阵时加入核函数，用来解决非线性映射问题。KPCA在高维特征空间对原数据映射，经过PCA对高维数据计算特征向量及特征值来确定主成分因子。

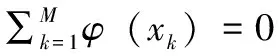
(1)

通过特征分解C值得出：

λν=Cν

(2)

当所有特征值λ≥0，v为由φ(x1)，φ(x2)，…，φ(xM)组成的空间，所以式(2)等于：

λ(φ(xk)，vr)=(φ(xk)，Cvr)k=1，2，…，M

(3)

由于vT是φ(x)的线性组合，所以得出：

(4)

将式(1)、(4)代入式(3)，并令Kij=(φ(xi)，φ(xj))i，j=1，2，…，M，代入得出：

Mλrcr=Kcr

(5)

Mλr为特征值，cr为特征向量，当满足cr>0条件：cp，cp+1，…，cM，进行归一化后得出：

Mλr(cr，cr)=1

(6)

求得φ(x)在cr特征向量的投影：

r=p，p+1，…，M

(7)

g(x)为φ(x)非线性主元分量，g(x)[g1(x)，g2(x)，…，gI(x)]T为所有投影矢量表示。使用核函数K(xi，xj)=〈φ(xi)，φ(xj)〉求解g(x)代替空间的点积运算，核函数变为：

g(x)=(vT，φ(x))=K(xi，xj)

(8)

当φ(x)≠0时，空间样本变换：

(9)

通过式(8)计算矩阵K，再依据样本变换求取特征向量与特性值，最后依据最大特征值及其对应向量结合输入属性得到主成分。按照式(10)、(11)得出各个成分的贡献率与累计贡献率。

(10)

(11)

1.2 LSSVM模型

LSSVM(least squares support vector machines)[14-15]基于SVM将不等式约束转换为等式约束，从而化简lagrange乘子α求解，对求解QP问题转为进行线性方程组的求解。LSSVM 继承了 SVM 的泛化能力和鲁棒性，但其计算效率优于原始的 SVM。给定训练的数据集合(xi，yj)，i=1，2，…，n，分别给出SVM及LSSVM需求解的问题。

SVM不等式约束问题：

s.t.yi[ωT·φ(xi)+b]≥1-ζi，i=1，2，…，n

(12)

LSSVM等式约束问题：

s.t.yi[ωT·φ(xi)+b]=1-ei，i=1，2，…，n

(13)

ξ及e为松弛变量，用于SVM及LSSVM中引入离群点，c及γ为平衡寻找最优超平面与偏差量之间最小值，ω为权重向量，b为误差，φ(·)为映射函数。

使用Lagrangea方法对式(13)优化，转化为单一的参数，求解α的极限值，构造出：

L(ω，b，e，α)=

(14)

其中：αi为拉格朗日乘子。

ω，b，ei，αi分别求导=0：

(15)

φ依据4个求导的条件可列出线性方程组：

(16)

In为单位矩阵的转置矩阵，E为n维单位矩阵，Φ为核矩阵：

Φij=yiyjφ(xi)Tφ(xj)=

yiyjK(xi，xj)，i，j=1，2，…，n

(17)

解方程(16)，可得出一组α、b，最后得出LSSVM分类表达式为：

(18)

LSSVM的训练框架如图1所示，LSSVM算法中的正则化系数和核函数参数需要进行寻优防止出现参数随机导致的精度不佳问题及过早收敛导致陷入局部最优的问题。

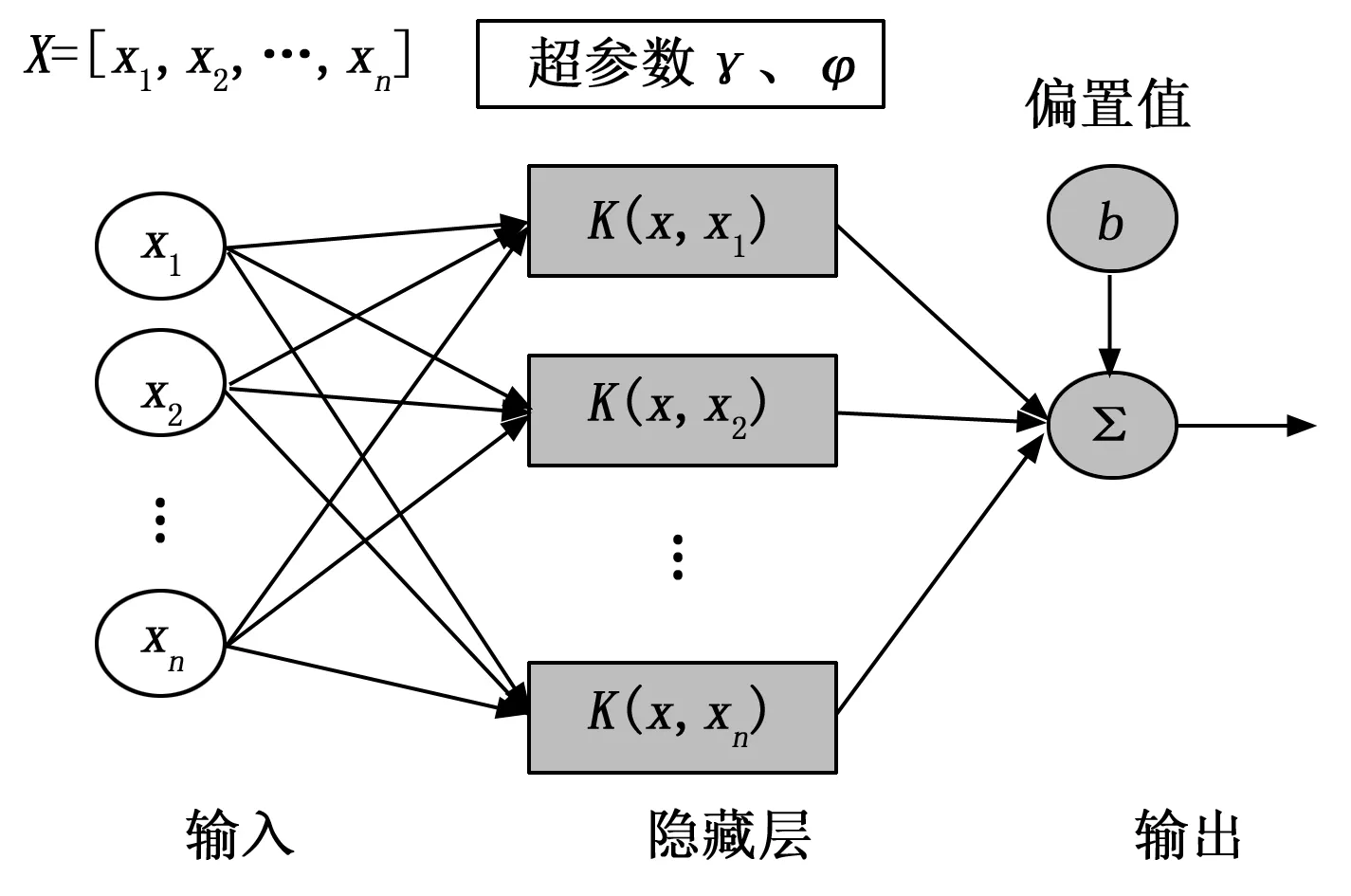
图1 LSSVM模型网络结构图

1.3 松鼠觅食算法

松鼠觅食算法(sparrow search algorithm)[16]对于搜索空间中的一些复杂问题搜索能力及精度有明显优势，松鼠虽不会飞行，但可以通过滑翔的方式来躲避天敌捕食，SSA算法就是模拟其这一行为的过程。松鼠的搜寻过程伴随其觅食的开始，寻找食物的方式通过其从不同的树木之间移动来获取，森林中不同区域的搜索通过松鼠位置的改变来实现。

假设松鼠的数量为n，松鼠移动的位置通过矢量来确定，并在边界范围内随机初始化其位置。

(19)

FSn，d为第n只老鼠在第d维度上的值，松鼠在森林中的初始位置为：

FSi=FSL+U(0，1)×(FSU-FSL)

(20)

FSU和FSL为松鼠移动的上下界，U(0，1)为随机数[0，1]。

食物源的等级通过每一只松鼠位置的适应度表示，计算适应度值并进行升序分类，适应度最小的位置：最佳食物源①山核桃，接下来三只位置正常食物源②橡树，其他的位置无食物来源③普通树。

依据其天敌的出现概率Pdp松鼠更新移动的位置。

滑翔路径一：②→①

(21)

滑翔路径二：③→②

(22)

滑翔路径三：③→①

(23)

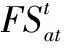
季节的变化会影响松鼠的觅食活动，使用季节的变换来防止出现算法陷入局部最优。

(24)

(25)

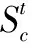
(26)

FSi，U和FSi，L为松鼠移动的上下界，Levy为列维分布，有效地全局搜索，来找到距离当前地点最优的一个新地点。SSA算法具体步骤如图2所示。

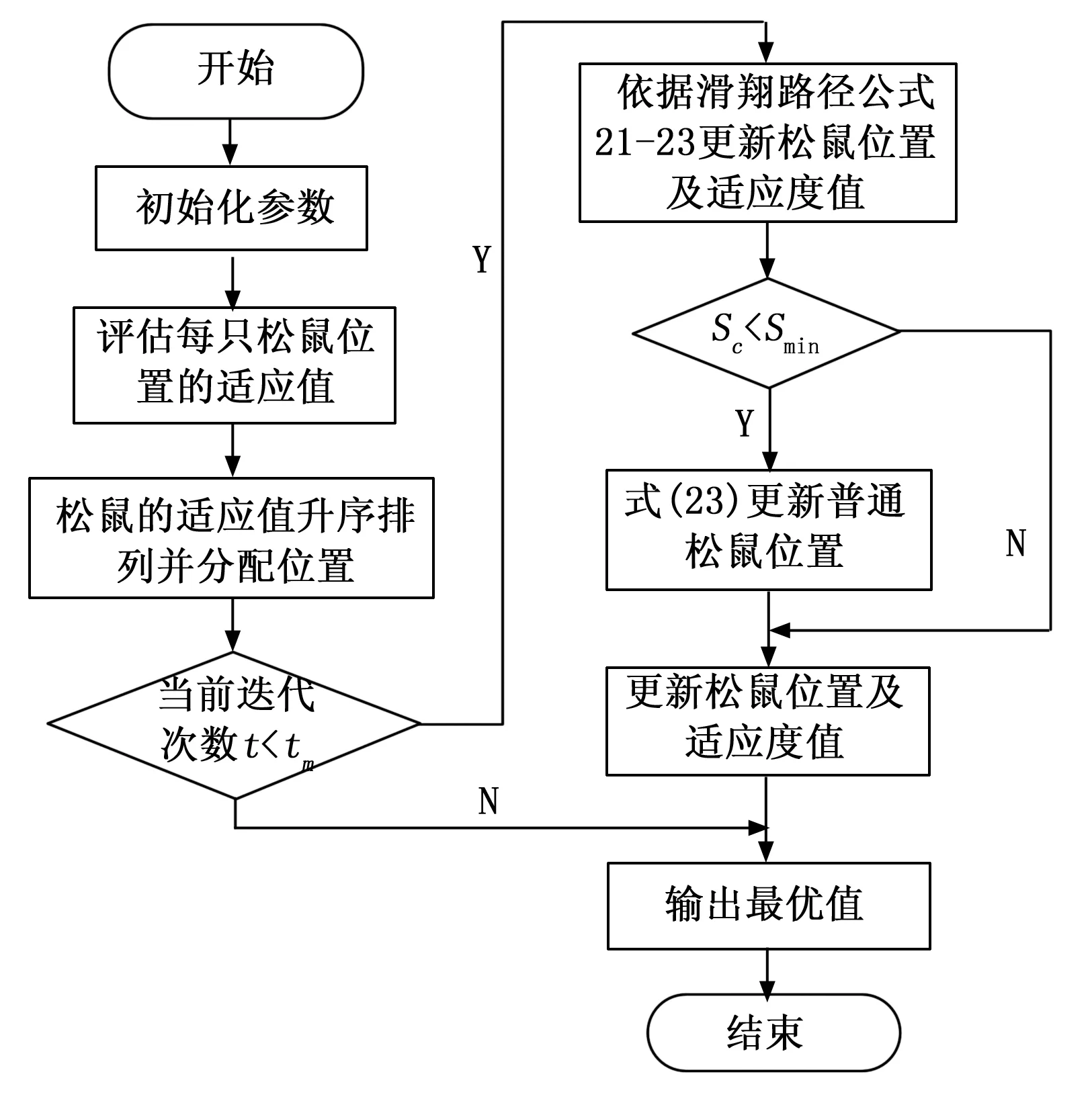
图2 SSA算法流程

2 基于KPCA-SSA-LSSVM山区泥石流灾害预测模型

基于KPCA-SSA-LSSVM的山区泥石流灾害发生预测流程如图3所示，具体实现步骤如下：

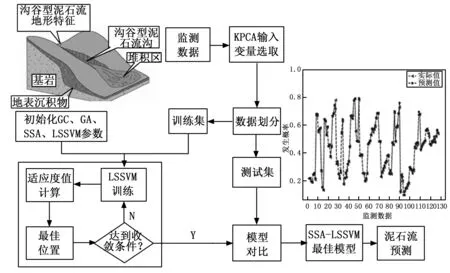
图3 KPCA-SSA-LSSVM算法流程

1)首先对监测的原始数据预处理，并使用KPCA核主成分分析法筛选出覆盖率满足需求的6个影响因子。

2)数据集合理划分，确定训练集及测试集百分比。

3)初始化寻优参数及LSSVM参数。

4)根据各影响因子建立LSSVM预测模型，并在训练集训练最佳适应度函数。

5)将不同预测模型在测试集上分析对比，筛选得出最佳模型及预测结果。

3 仿真验证和结果分析

3.1 研究区概况及数据来源

陕西省商洛市山阳县的中村镇，因其地处秦岭山下，山脉沟壑众多，属于中、低山地形，山体土石量多达180多万方，占地高达80%以上，位于地势差异较大的峡谷地区，地形地质复杂，山体石量多，更易引发灾害。同时也属于长江流域汉江水系，地区水源较多，河流较多、尤其在夏秋季降雨量也较多，年平均降水量达到671～865毫米，如果连续降雨量大容易导致土质疏松[17]，从而增加了地质灾害的安全隐患点。

参照《T/CAGHP 006-2018泥石流灾害防治工程勘察规范》、《滑坡崩塌泥石流灾害调查规范(1：50 000)(DZ/T0261-2014)》[18]结合山阳县实地监测区域监测泥石流活动数据，对泥石流发育机制及成灾特征分析，本研究区域按照水源和物源成因划分为崩塌型泥石流，其中固体物质主要由滑坡崩塌等重力侵蚀提供[19-20]。去掉规范量级评分表中5分以下影响因子，最后结合监测区实际泥石流数据得出11个影响因子，分别为沟岸山坡坡度、降雨量(24 h、1 h、10 min最大降雨量)、土壤含水率、沟床平均坡度、岩性影响、流域相对高差、河沟堵塞程度、河沟纵坡、产沙区沟槽横断面、松散物平均厚度、流域面积、泥砂沿程补给长度比、孔隙水压力、沿沟松散物量、区域构造影响、流域植被覆盖率。因各降雨量24 h、1 h、10 min最大降雨量对泥石流的发生有极大的影响，所以选取暴雨强度R作为泥石流灾害模型的影响因子。暴雨强度R计算如式(27)，各参数选取如表1所示。

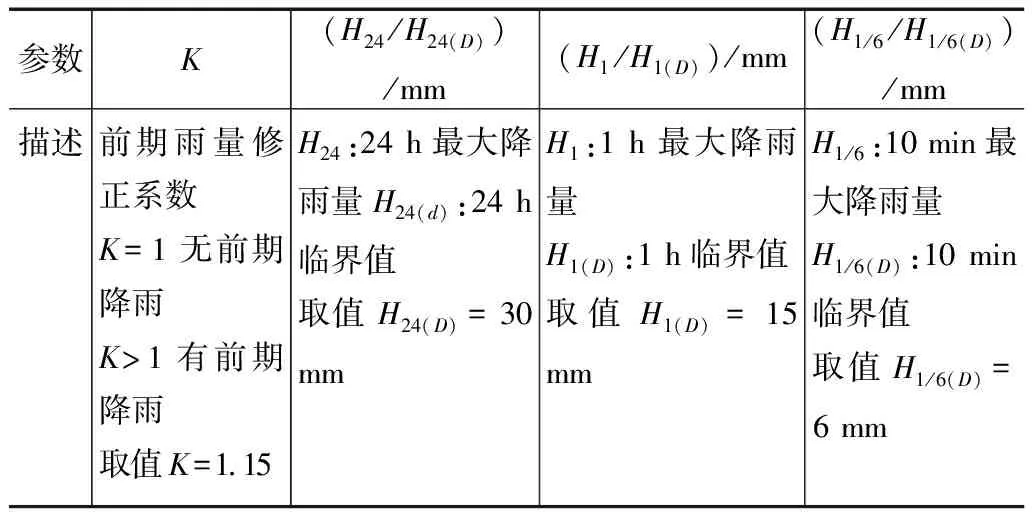
表1 泥石流降雨量因子参数

R=K(H24/H24(D)+H1/H1(FD)+H1/6/H1/6(D))

(27)

3.2 数据预处理

监测数据由于环境的影响会出现一些如缺失、离群或维度不统一的数据，这些数据对于模型的建立有极大的消极影响，会产生跳跃，且无法与其他数据统一，因此需要对监测数据进行预处理。

1)异常值处理：监测数据中存在一部分偏离传感器本身范围的值或偏离观测值较大的值，不处理会影响数据预测准确性，距离达到5倍或者与均值的距离≥3倍标准差的数据称之为离群点。

2)缺失值的处理：监测数据通过泥石流灾害区域多传感器实时传输，传输过程中经常会出现遗漏或者个别离群点情况，会出现失真损失有效信息，导致属性值缺失不准确。按照属性因素方法进行统计得出缺失率，本文划分两种类别数据的缺失值，如表2所示。

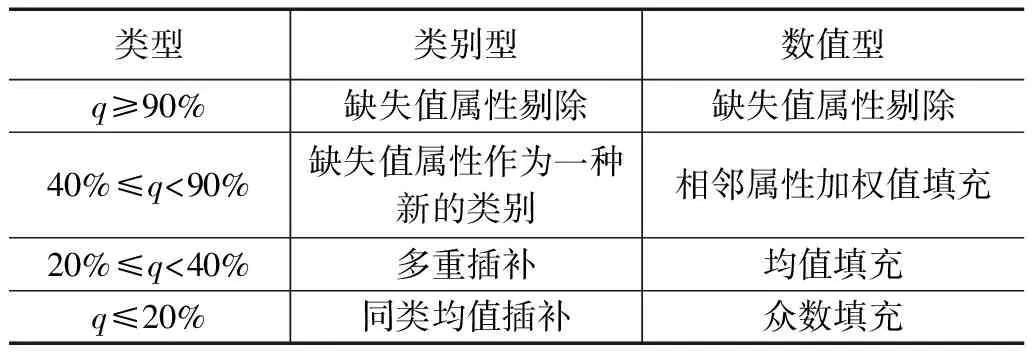
表2 数据缺失值

3)数据归一化：监测数据种类较多样且数量较多，多传感器数据量纲不同有较大的差异，使用原始数据直接建模对于预测的准确性有极大的影响，所以需要对数据进行归一化处理，归一化处理公式如(28)：

(28)

式(28)中，R为某因素归一化处理后的数据，Rmin和Rmax表示某因素数据中的最小值及最大值。

3.3 数据影响因子筛选

由于样本影响因子彼此之间存在相关性，为避免相关性对预测结果的影响，本文通过KPCA核主成分分析法选取成灾因子，各主成分的特征值及贡献率如图4所示，实验表明前6个主成分的累计的贡献率已经达到95.48%，覆盖的信息超过了90%，覆盖率达到要求，所以文中选取前6个影响因子作为泥石流灾害模型训练的输入数据。并依据《T/CAGHP 006-2018泥石流灾害防治工程勘察规范》及泥石流相关资料分析，得出影响因子与泥石流发生量化等级关系如表3所示。以陕西省山阳县重点地灾监测区的历史数据作为研究样本，数据使用山阳县2019年4月到2021年4月的10个监测点的数据作为数据集，经过数据预处理及成灾因子选取后数据集总共筛选出1 300组数据，分别分为80%测试集和20%的两个验证集。

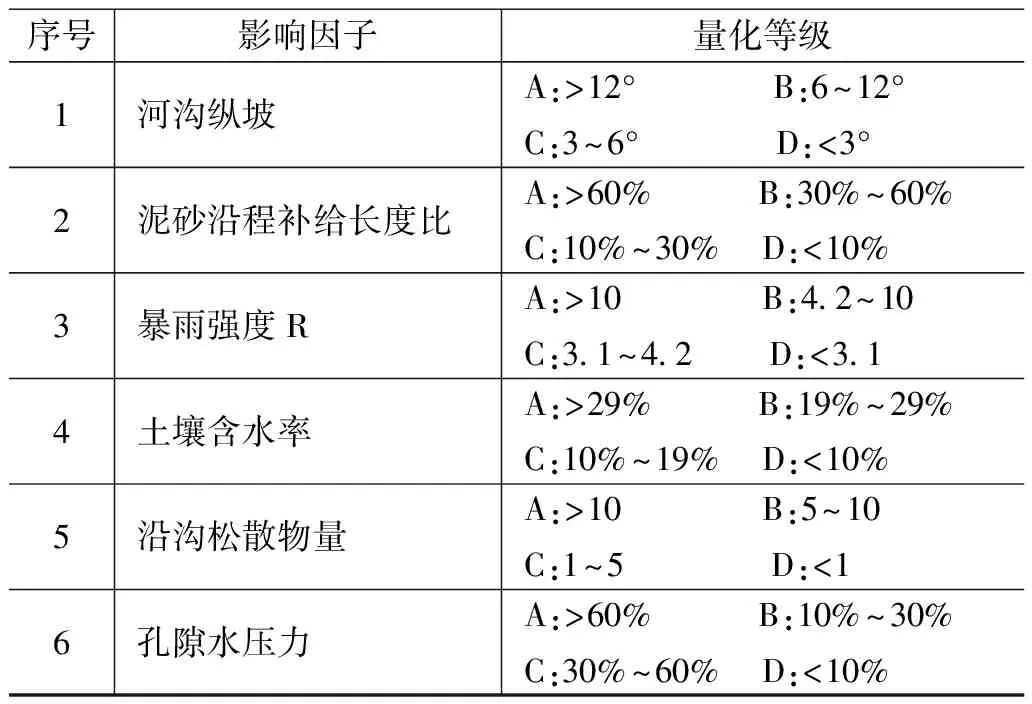
表3 泥石流影响因子量化表

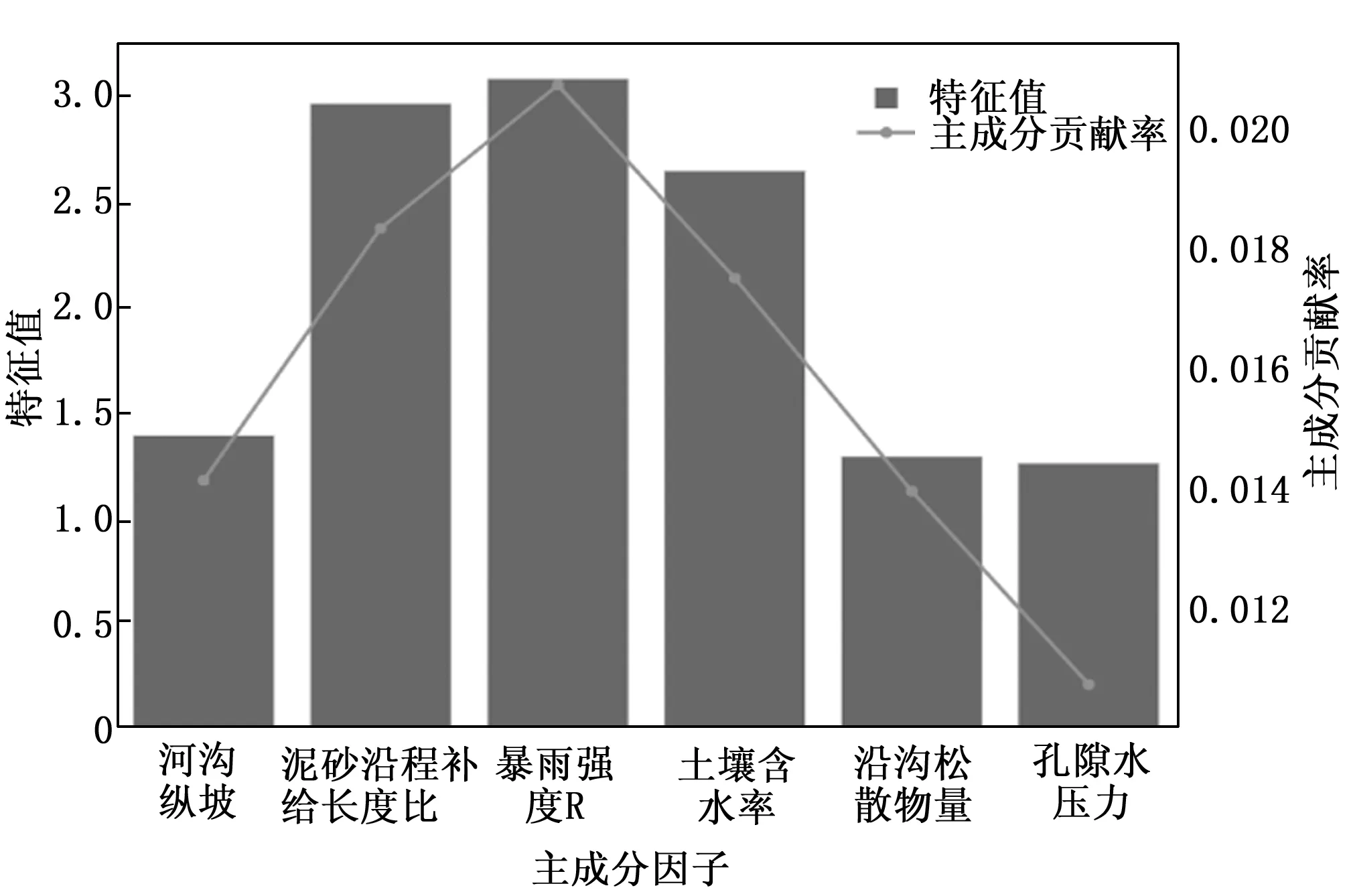
图4 影响因子特征值及主成分贡献率

注:A.泥石流发生严重;B.泥石流中等发生;C.泥石流轻微发生;D.泥石流不发生。

3.4 超参数寻优

LSSVM建模过程中调优参数为正则化系数和核函数φ参数，文中选取SSA寻优算法与遗传算法 (GA，genetic algorithm)及网格搜索(GC，gridsearchCV)在相同1 040组训练集对LSSVM模型的正则化系数γ和核函数φ参数进行寻优。种群的规模设置为90，最大迭代次数设置为200，每个优化算法分别进行60次独立实验，并分别画出最优适应度函数值与迭代次数曲线图进行比对，结果如图5所示，适应度函数值随着迭代次数的增加而逐渐减小，最终搜寻到最优参数后收敛。GC在第16次迭代大幅下降。跳出了局部最优状态，GA整个迭代过程收敛速度较慢，但也逐渐趋向最优，SSA优化效果最好，明显引导种群向最优位置处，说明使用SSA算法寻优，对松鼠移动的位置不断调整可以跳出局部最优值，且收敛速度快，而且早熟现象明显，能够取得更小的适应度。最终选取正则化系数γ=0.274和核函数φ=7.642。

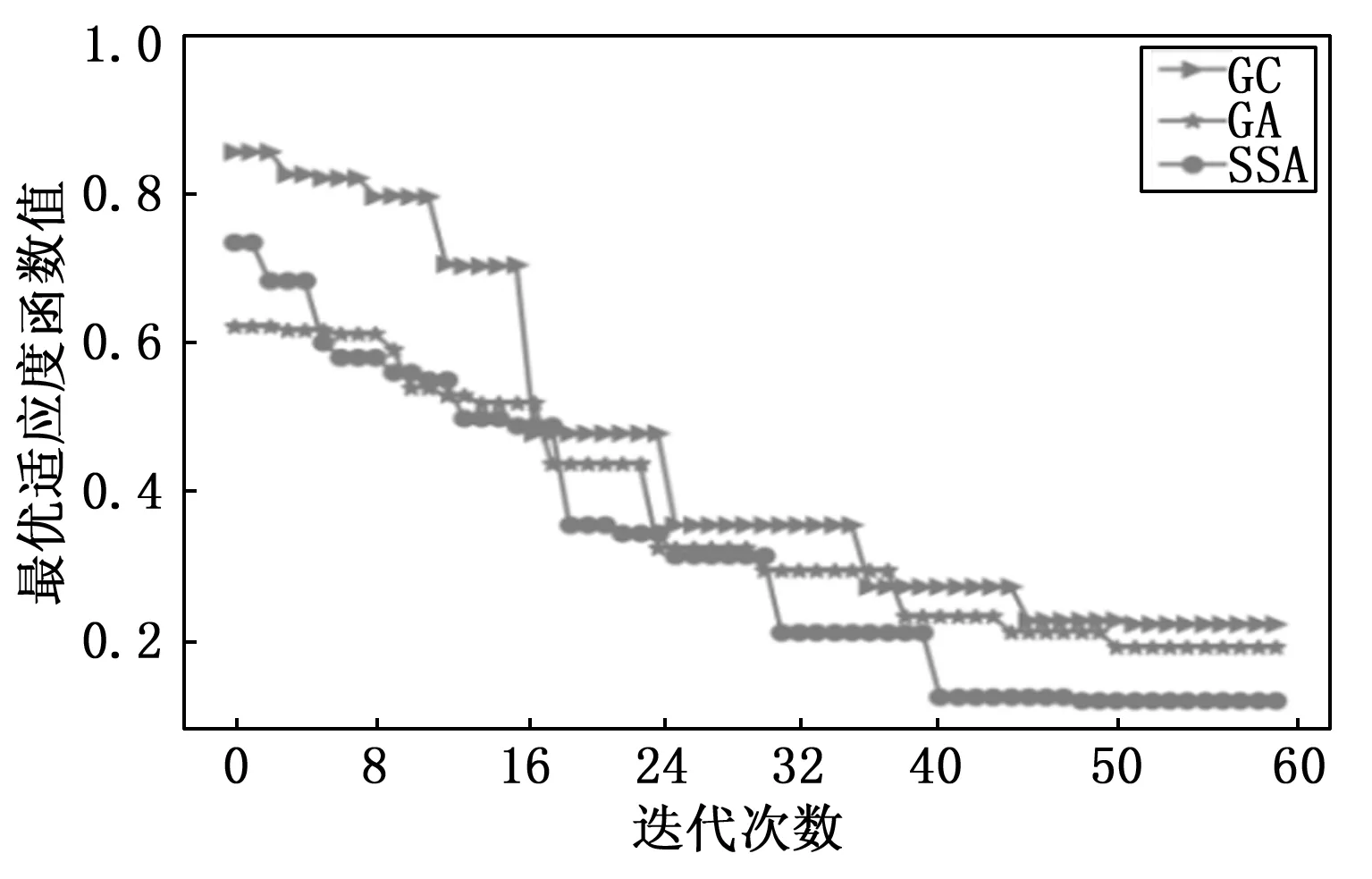
图5 寻优适应度曲线对比图

3.5 仿真验证及结果分析

为验证模型的预测精度，引入模型评价指标AUC值，其为ROC曲线结合坐标轴围成的面积值，范围一般介于[0.5～1]之间，预测的真实性取决与AUC值接近1的程度，靠近1真实性高反之则反。MAE预测值真实误差，RMSE预测值和真实值间偏离程度，MSE真实值与预测值差异，越接近零预测精度越高，如式(29)所示：

(29)

为验证本研究优化模型的准确性，将经过数据预处理及降维后的训练数据作为泥石流预测模型构建的输入数据，总共1 040组训练集构建泥石流预测模型，并通过10%验证集1验证各模型的准确性。实验采用LSSVM作为泥石流灾害预测模型，并用SSA算法超参数寻优。使用同一个验证集验证未优化的LSSVM模型及其他寻优算法对LSSVM预测效果比对。利用预测结果计算模型的MAE、MSE和RMSE，值越接近于零精度越高，可以看出SSA-LSSVM的MAE、MSE和RMSE最小且接近于零，对比评估指标结果如图6所示，传统的LSSVM相对误差较大，最大相对误差达到1.72%，而SSA-LSSVM最大误差达到0.19%，误差是最低的，进一步说明了该模型预测的精度较高。

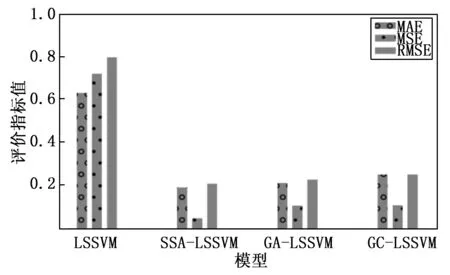
图6 模型预测评估指标

为进一步验证模型的稳健性，选取10%验证集2，将其打乱的130个监测数据作为模型预测概率及预测等级误差的评价，图7为各模型寻优LSSVM模型后的实际发生概率与预测发生概率比对图。SSA寻优后实际值与预测值基本吻合，拟合情况较好，极限的几个数据27、38、89及111发生概率存在一些差异，但是其对应的风险预报等级与实际数据风险等级结果吻合，不影响预报的等级，多个算法模型在同一预测集上的预测等级结果如图8所示，按照泥石流发生等级准确率降序排列：SSA达到100%，GA-LSSVM达到92.3%，GC-LSSVM达到90%。实验说明引入SSA对LSSVM参数寻优，泥石流发生的概率及等级预测准确率皆有明显的提升。使用寻优后的SSA-LSSVM模型对研究区域泥石流进行预测，从发生的概率及预测的等级两方面都证明该模型具有较高的可行性。

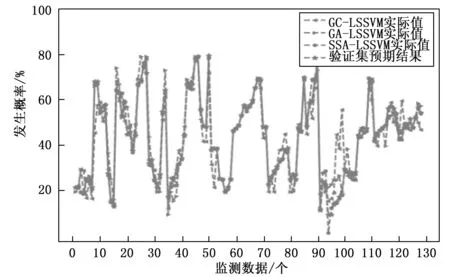
图7 模型预测预测比对图

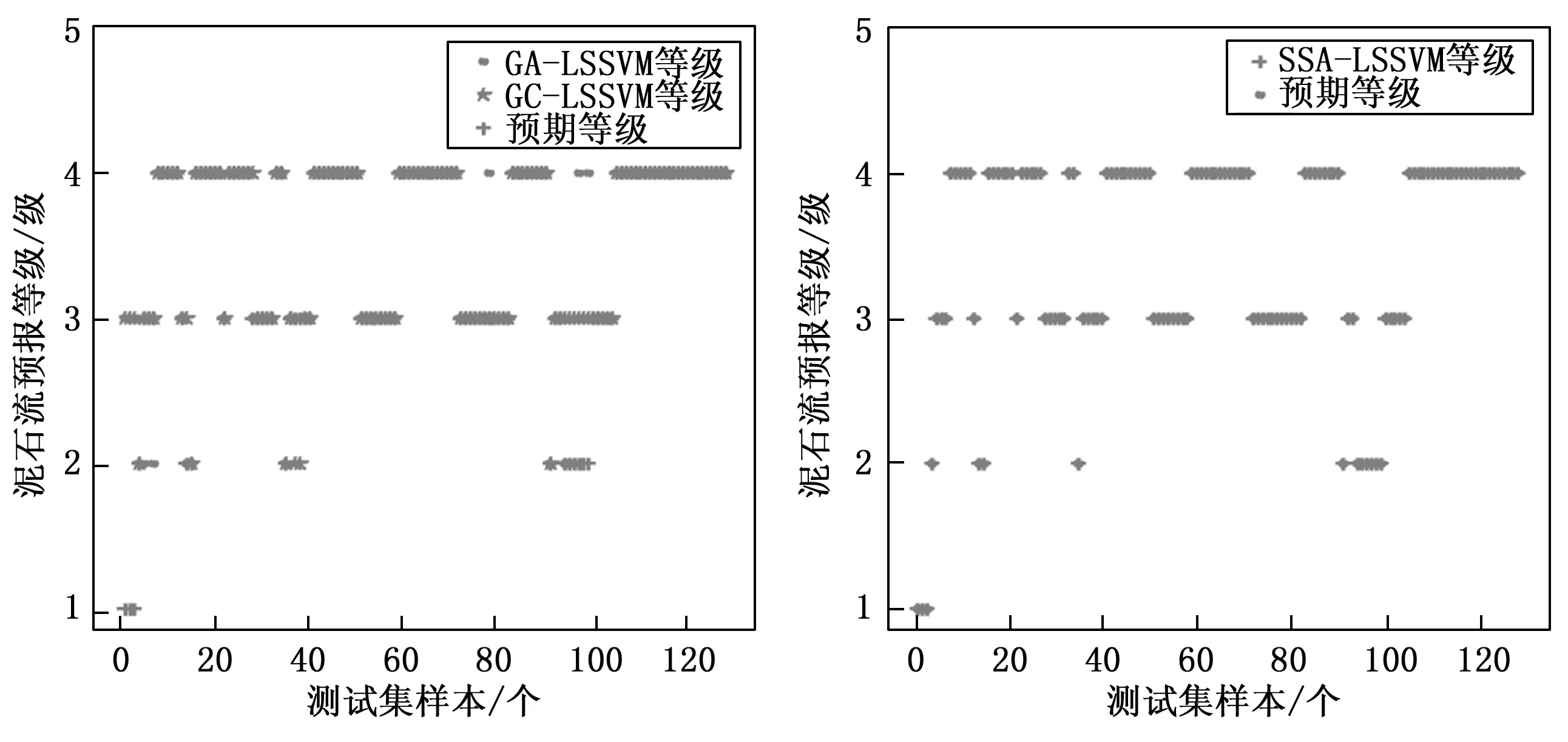
图8 发生概率等级预测图

此外通过AUC公式计算得出20%验证集中各模型的ROC曲线如图9所示，ROC曲线中横坐标为假阳性率(FPR/1-Specificity特异度)，纵坐标为真阳性率(TPR/Sensitivity)，可以根据ROC曲线的面积下的AUC值看出各个预测模型对应评价指标的好坏，AUC值越高说明模型精度越佳，各模型AUC值均高于0.88，但是SSA-LSSVM模型指标更加，无论从测试时间、AUC值及ROC曲线均明显优于GA和GC寻优模型，模型AUC均值为0.932，预测效果较其他模型理想。各模型的对比指标参数如表4所示，SSA-LSSVM模型相比其它模型平均测试事件最短且平均AUC值最高且接近于1。多组实验数据结果证明SSA-LSSVM模型具有较好的预测效果，在泥石流灾害预测中有较好的预测能力。

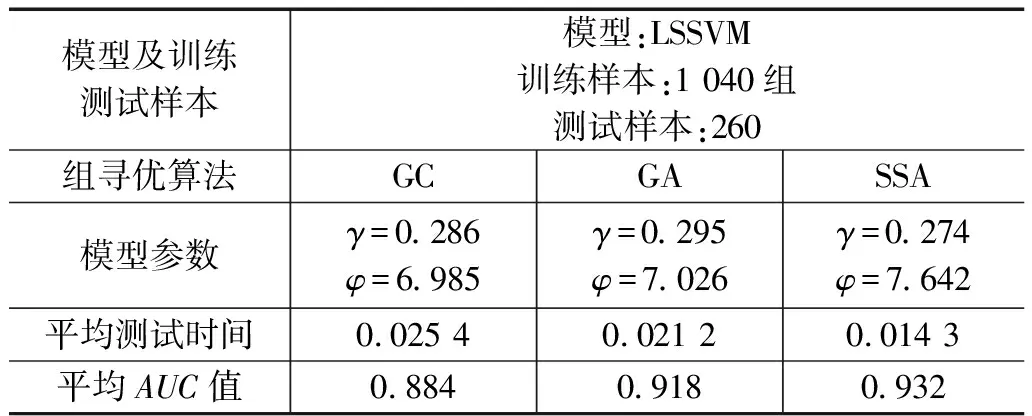
表4 模型参数及结果比对

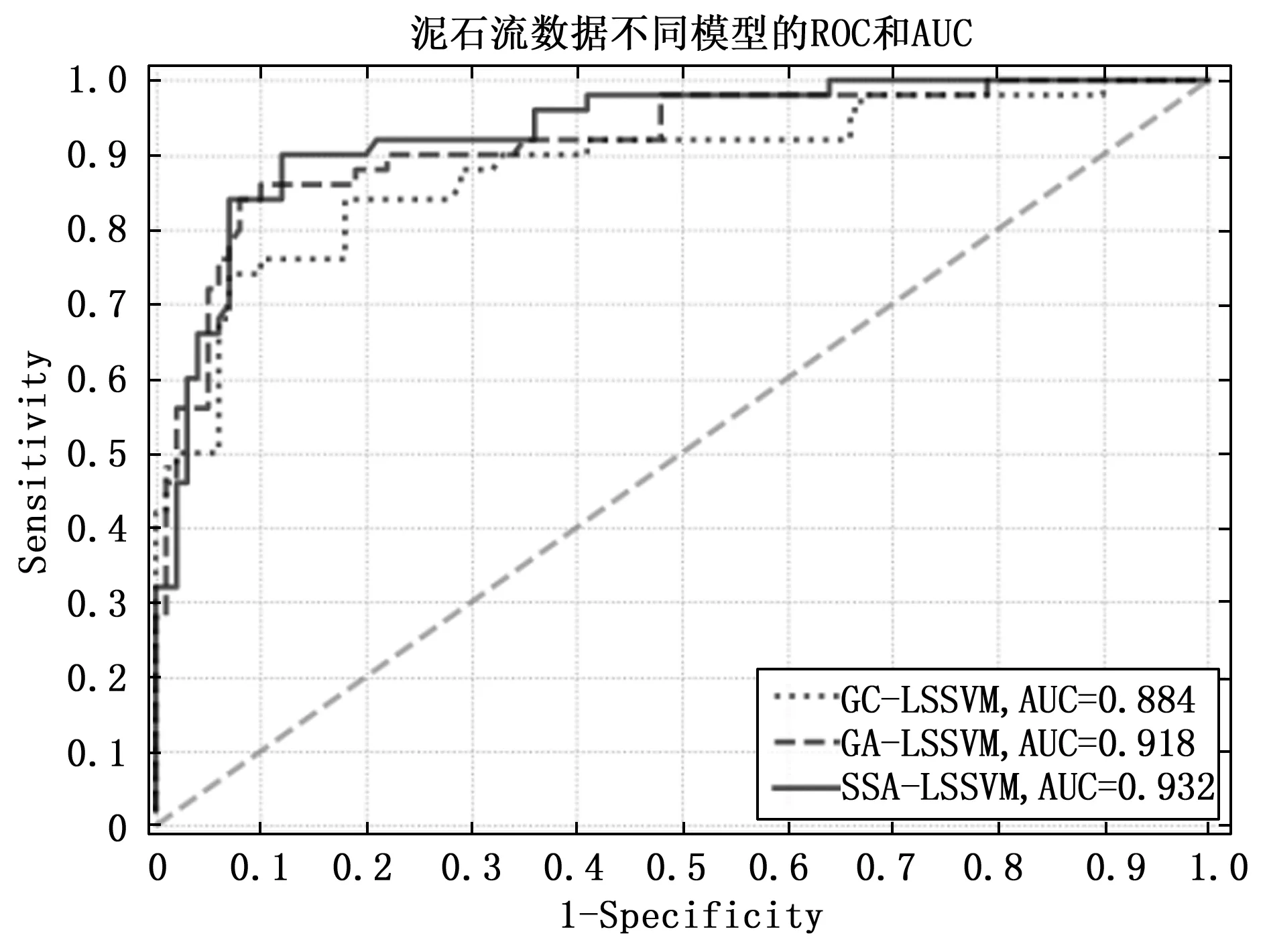
图9 模型ROC曲线

4 结束语

本文以普适的山阳县中村镇区域泥石流为例，结合泥石流全域的地形地貌成灾机理，提出KPCA-SSA-LSSVM泥石流预测模型，在研究区实践应用效果良好，说明模型具有一定的可行性和有效性。因此，可以得出以下结论：

1)参照《T/CAGHP 006-2018泥石流灾害防治工程勘察规范》、《滑坡崩塌泥石流灾害调查规范(1：50 000)(DZ/T0261-2014)》并结合山阳县实地监测区域，监测泥石流活动数据，对泥石流发育机制及成灾特征分析，选出11个成灾因子，并使用KPCA主成分分析法依据因子的贡献率筛选出6个重要的成灾因子；

2)LSSVM建模过程中调优参数为正则化系数和核函数参数，选取SSA寻优算法与遗传算法 (GA，genetic algorithm)及网格搜索(GC，GridSearchCV)在相同1 040组训练集对LSSVM模型参数进行寻优，解决参数随机导致的精度不佳问题及陷入局部最优问题。

3)将寻优后的SSA-LSSVM预测结果与GA、GC参数寻优模型预测结果比对，从AUC值、MAE、MSE、RMSE评价指标都验证了SSA-LSSVM预测的精度。

4)使用寻优后的SSA-LSSVM模型对研究区域泥石流进行预测，从发生的概率及预测的等级两方面都证明该模型具有较高的可行性。