基于应变阵列的小型表面冲击定位系统设计

文聪楠，王晓燕，薛英娟，张晓明

(1.中北大学 电子测试技术国家重点实验室，太原 030051；2.北京航天飞腾装备技术有限公司，北京 100094；3.中北大学 创新创业学院，太原 030051)

0 引言

2011年叙利亚内战初期，有关资料显示[1]，武装分子肆意在坦克近距离徘徊，驾驶员只能坐在驾驶舱内通过车长镜[2]或者车身窗口观测，完全对车身外部装甲健康状态失去判断能力。装甲单位对自身外部的观察手段有限，尤其是坦克、自行火炮等重火力装甲单位，其战场机动性相较于轻火力单位差，在深入步兵集群内部或陷入遭遇战时通常会有自检手段少、自身健康信息不足等问题，往往依靠人工舱外作业的方式来判断外层装甲的健康程度，危险程度大；且其内部空间狭小，无法放置大型测量设备。目前并没有一种小型化、低成本、内嵌式的装甲表面冲击定位技术，能够使得舱内人员在不暴露软目标的情况下对外层装甲的状态有一定程度的判断。

对于固定表面的冲击定位技术，学者们进行了大量的研究与讨论，根据冲击的传感测量方式，大致分为光纤光栅传感冲击定位[3-6]、压电传感冲击定位[7-8]和应变传感冲击定位[9]。应变传感的冲击定位方法在适应性和经济性上明显优于光纤光栅传感和压电效应传感的表面冲击定位方法，更适合易损件的表面冲击定位。

1 测量系统总体结构

本文设计了一种基于应变阵列的小型表面冲击定位系统。系统具备多路信号同步采集、多路信号时差补偿、冲击坐标计算等功能。针对定位需求，设计应变传感阵列布置方式；从工程实际和设计目标出发，设计硬件电路，实现应变传感放大和多路同步采样的硬件功能；针对由于小型化设计带来的单ADC多通道采样的通道间时差现象，设计时差标定方案和插值补偿算法；最后通过广义互相关时延估算，提取到达时间差，利用TDOA定位算法，实现对装甲表面冲击的定位。系统总体技术流程如图1所示。

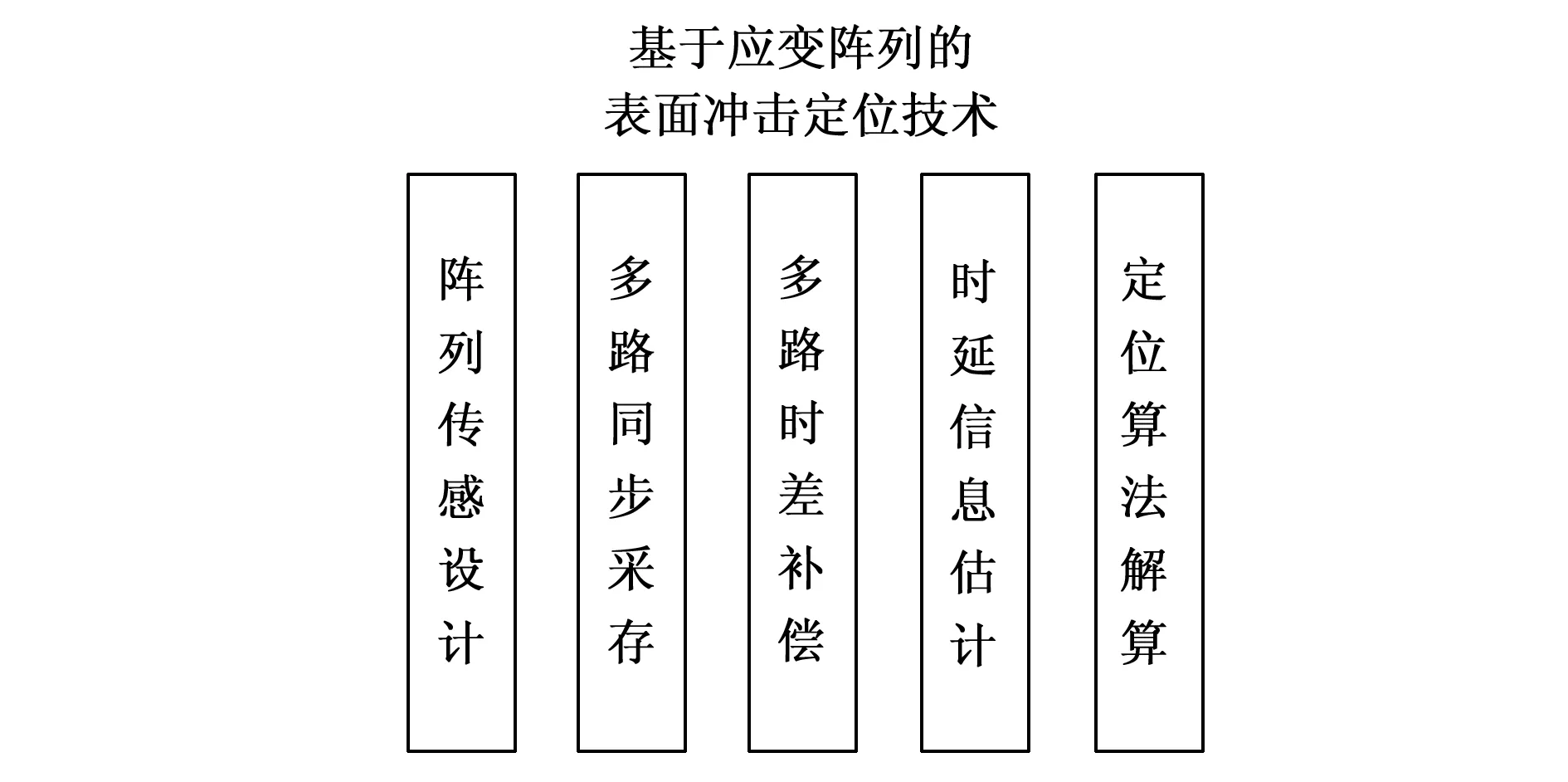
图1 系统技术实现流程

2 系统模块设计

2.1 应变阵列传感

粘贴在表面的应变片直接暴露在外部，虽然其体积很小，但实际战场上在遭遇密集轻火力打击时还是存在一定被击中的概率，针对本文设计需求，应将应变片嵌入到装甲板内部进行应变传感，采用在装甲板中夹装一种空腔震膜结构作为应变片的内嵌安装方式，如图2所示，其具体各层结构如图3所示。图中所有圆形空腔结构直径均为10 mm，线槽宽度为2 mm，图2中的两上下对称的空槽即为应变片的安装空腔，图3中的最中间层膜即为应变片的贴装薄膜，亦为震动薄膜。在最上层和最下层薄膜中预留线槽用以引出应变片引线，在有线槽的薄膜层和震动薄膜层中间夹焊一层无线槽但有空腔的金属薄膜，通过超声波焊接层层固结的方式对各层薄膜进行焊接固结，形成四周固定的圆形空腔震膜结构，其10 mm的直径不会对装甲板的防护性能产生过大影响。

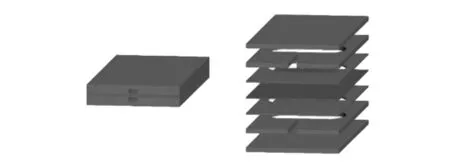
图2 空腔震膜结构示意图

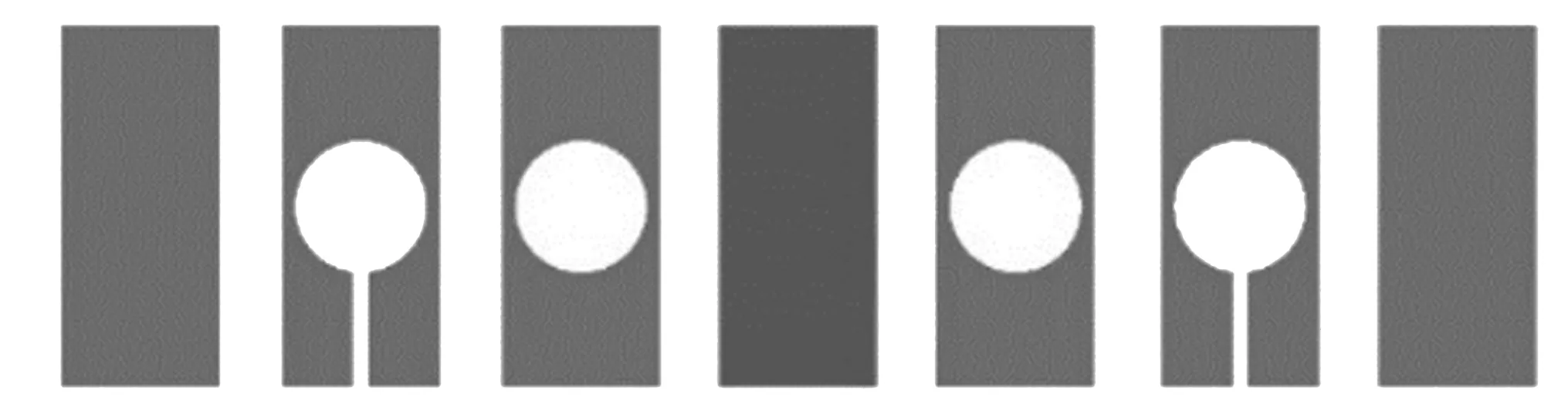
图3 空腔震膜结构各层俯视图

为了减小测量的非线性误差，使用惠斯通半桥电路将电阻值变化转化为方便测量的电压信号，如图4所示。惠斯通电桥因其使用方便，测量精度高等优点，成为被广泛使用的一种测量方法和手段[10]。将两个相邻臂的应变片对称粘贴到图2中的空腔内。半桥差动电桥电路的输出电压为：

图4 半桥电路示意图

(1)

设平衡时R1=R2=R3=R4=R，又ΔR1=ΔR2=ΔR，则：

(2)

装甲单位最外层的装甲板均为易损件，受击后要及时更换，为了提高战场适应能力和经济适用性，减少系统冗余，节约测试资源，应当在满足需求的前提下尽可能地减少阵列点数。考虑到后续硬件资源配置和算法应用，选择在一块装甲板上设计三个传感节点作为测量手段。在基于TDOA原理的平面定位系统中，其最终待测点的定位精度不仅与伪距的测量精度有关，也与各定位基站的平面几何位置关系有关。为了判断不同几何布局的应变阵列对定位精度的影响，引入精度因子值DOP(dilution of precision)[11]作为判断不同阵列布置方式定位精度水平的依据。针对本文需求而言，需要关注的就是平面精度因子HDOP(horizion dilution of precision)以及X轴和Y轴各自的精度因子XDOP和YDOP。

不同型号的装甲车辆有不同规格的装甲板，其形状大多为矩形，考虑用三个测量点覆盖一个矩形形状的被测范围，应将三个测量点都放置在装甲板的边缘位置。本文针对长宽不一的矩形装甲板设计了两种三角阵列布置方式，分别为长边中心的三角阵列布置和短边中心的三角阵列布置，当被测范围为正方形时，两种布置方式完全一致，以下以长宽比为2：1的矩形作为待测范围来比较两布置方式的定位精度水平。

长边中心的三角形阵列布置几何示意图如图5所示，图中虚线为各应变片敏感轴朝向示意。将一片应变片放置在被测矩形一长边AB的中心点F点处，其敏感轴朝向装甲板的中心点，两片应变片分别放置于相对长边CD的两角处，其各自敏感轴朝向均与各自邻边呈45°夹角，构成长边中心的三角测量阵列。

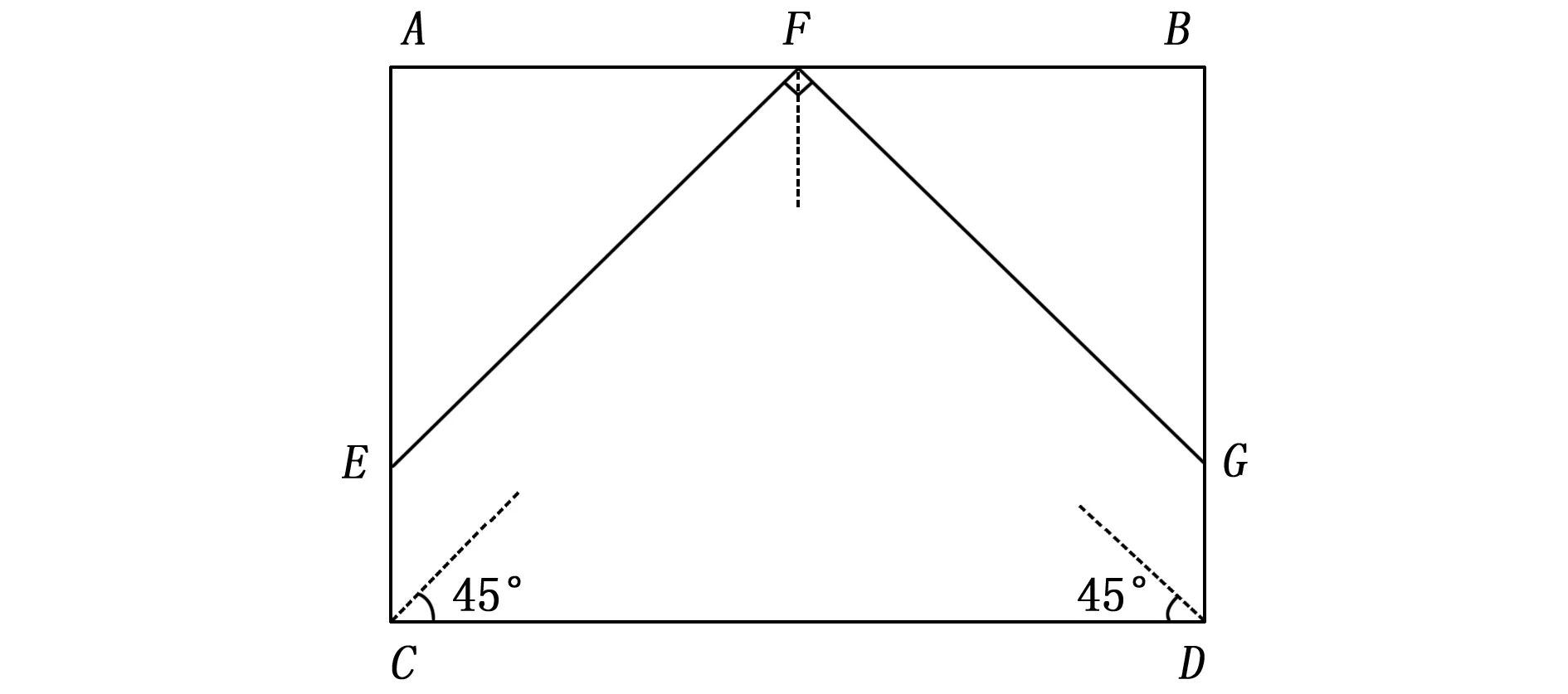
图5 长边中心的三角阵列布置几何示意图

绘制长边中心的三角阵列布置的三种精度因子等值线图，如图6～8所示。长边中心三角阵列布置方式的三种精度因子的均值、标准差与方差如表1所示。

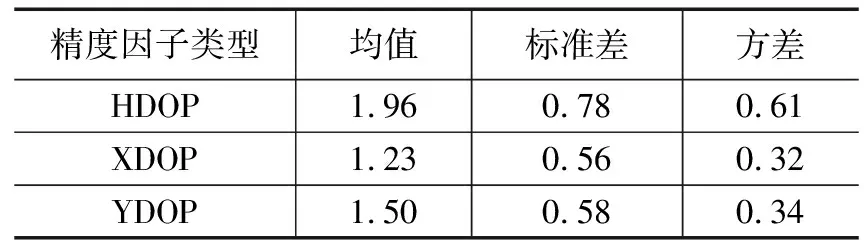
表1 长边中心三角阵列各精度因子均值、标准差与方差

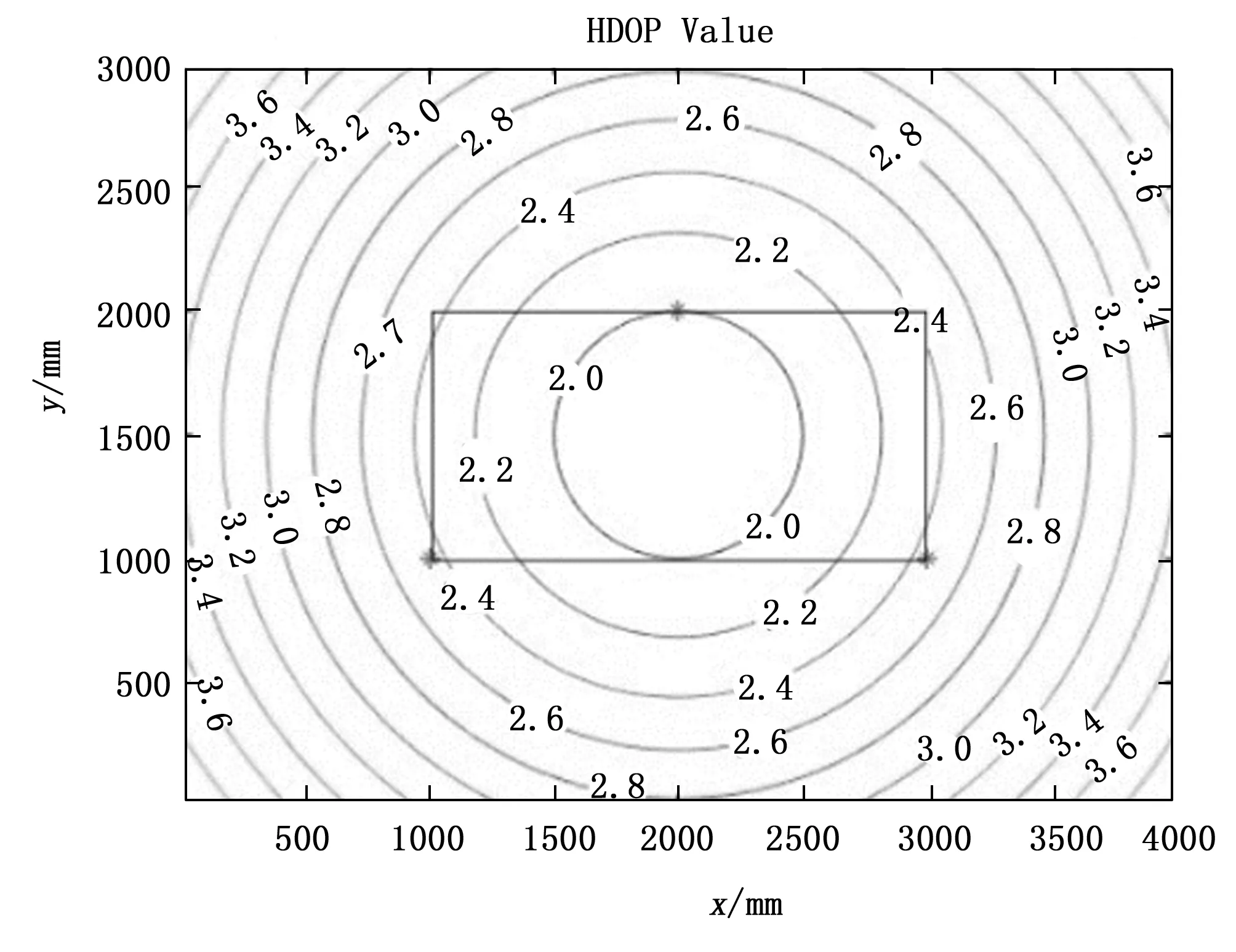
图6 长边中心的三角阵列HDOP值等值线

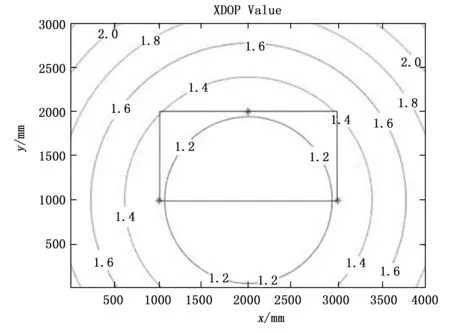
图7 长边中心的三角阵列XDOP值等值线

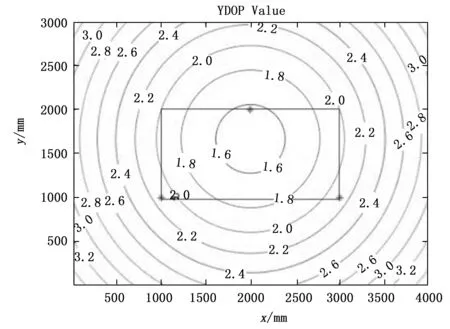
图8 长边中心的三角阵列YDOP值等值线

短边中心的三角阵列布置几何示意图如图9所示，图中虚线为各应变片的敏感轴朝向。与长边中心的布置方式相反，在短边AC中心点E点处布置一片敏感轴朝向被测范围中心的应变片，在相对短边BD的两角处B点和D点分别布置一片敏感轴朝向与各自邻边均成45°夹角的应变片，构成短边中心的三角阵列布置。

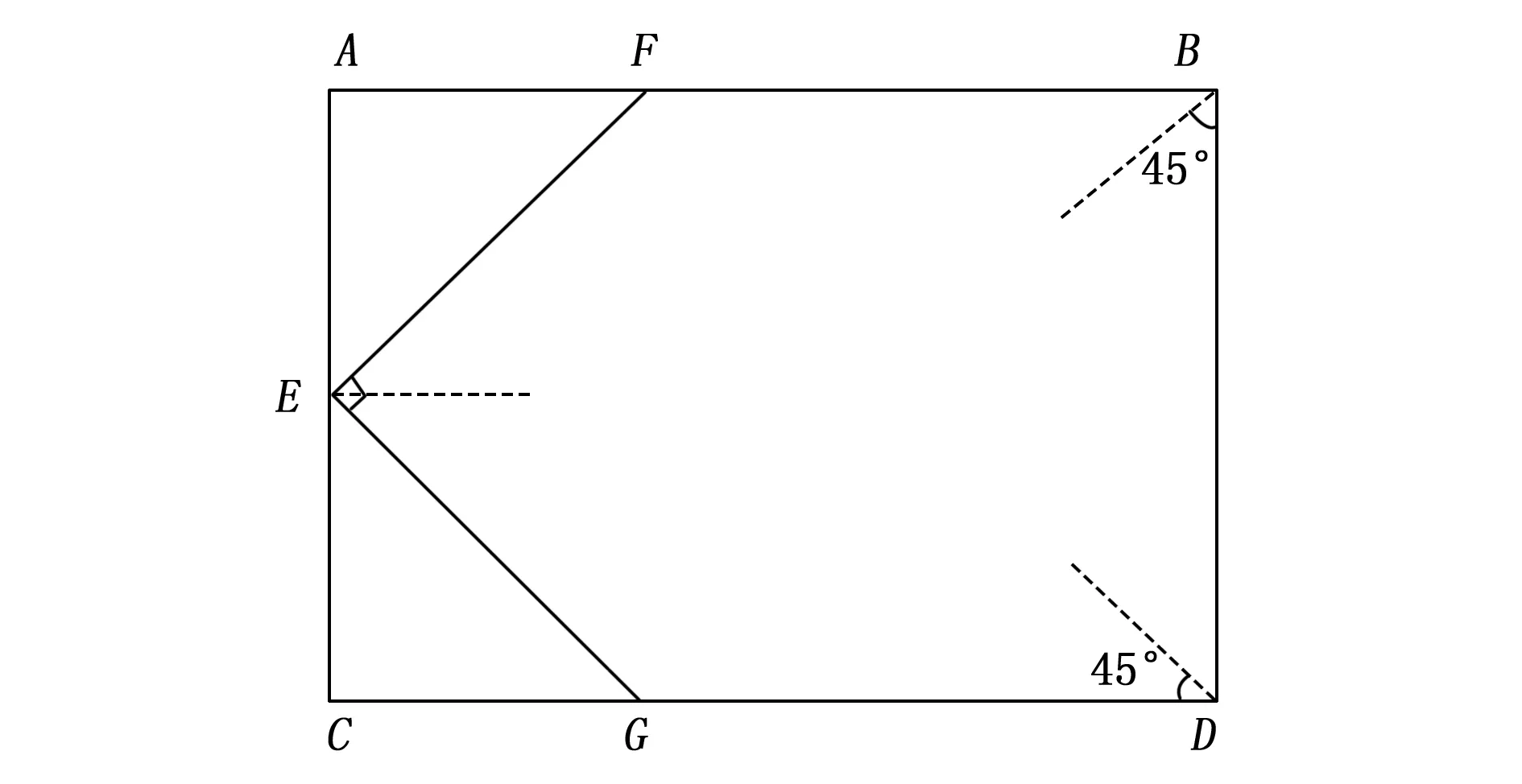
图9 短边中心的三角阵列布置几何示意图

选用长宽比为2：1的矩形作为被测范围，绘制短边中心的三角阵列布置方式的三种精度因子等值线图，如图10～12所示。

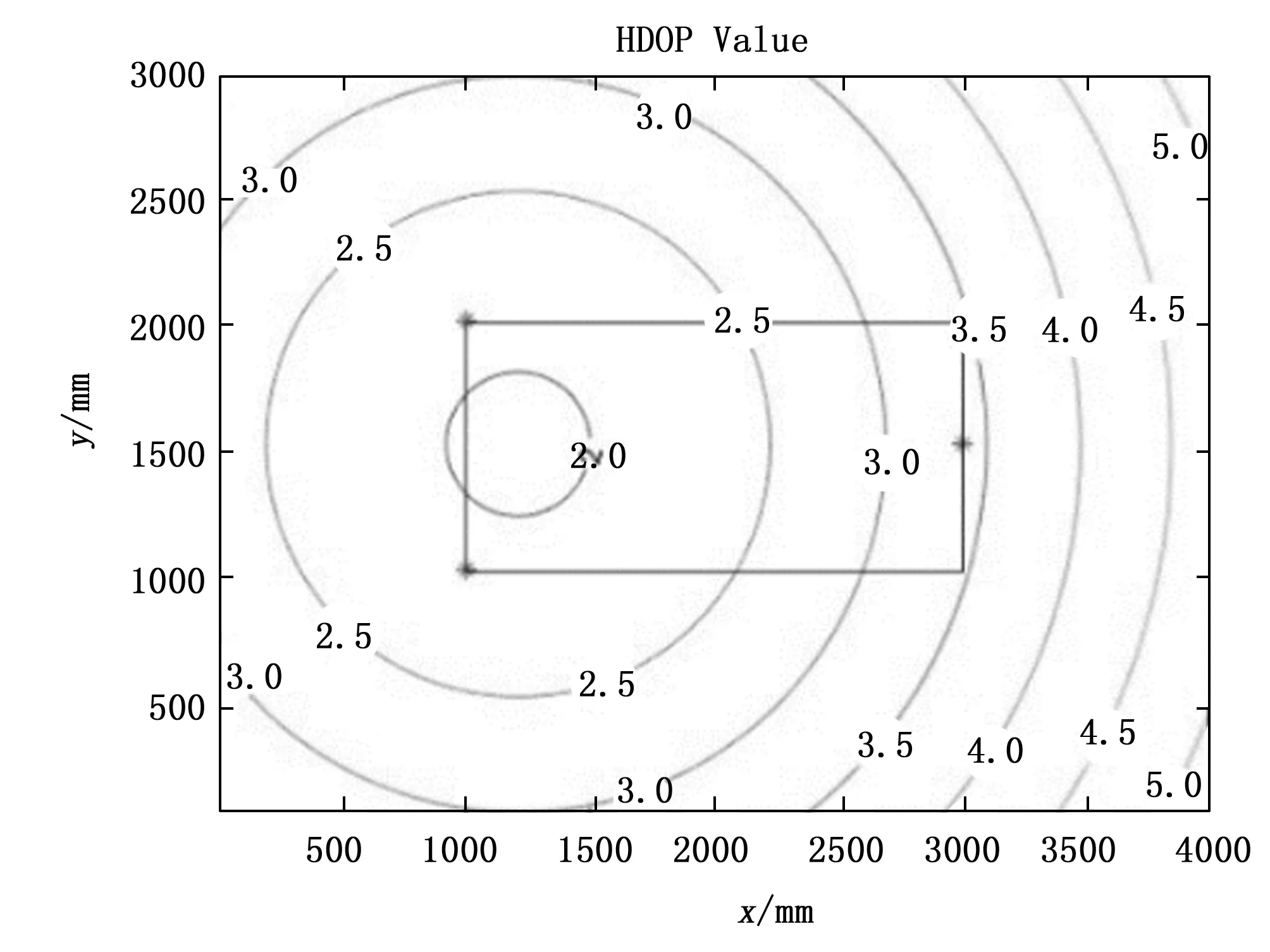
图10 短边中心的三角阵列HDOP值等值线

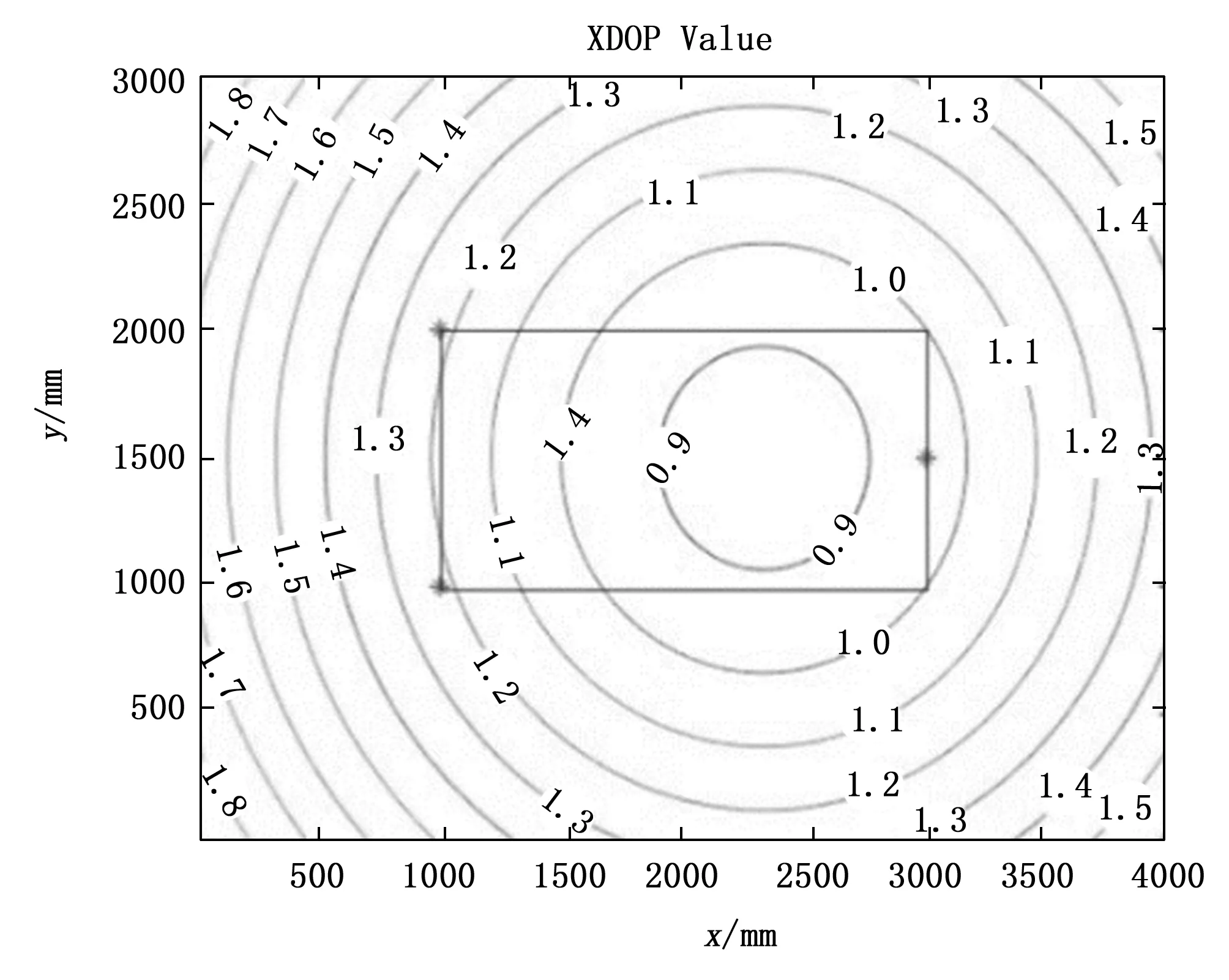
图11 短边中心的三角阵列XDOP值等值线

图12 短边三角中心的三角阵列YDOP等值线

根据各精度因子值的等值线图可知，在被测范围是长宽比为2：1的矩形时，待测位置越靠近有两个测量点的短边，精度因子值越小，定位精度水平越高；待测位置越靠近有1个测量点的短边的两角，精度因子值越大，定位精度水平越差，HDOP值最高达到3.5左右，XDOP值最高达到1.2左右，YDOP最高达到3.3左右。其三种精度因子的均值与方差如表2所示。

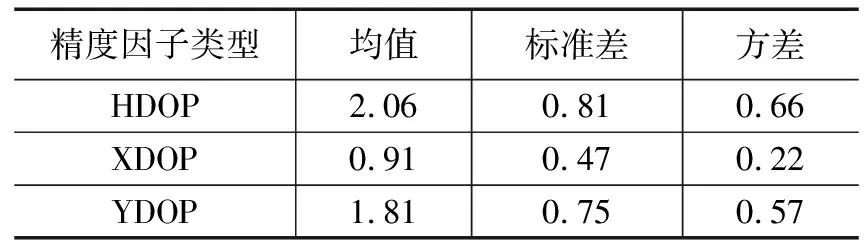
表2 短边中心三角阵列各精度因子均值、标准差与方差

对于两种阵列布置方式所计算得出的三种精度因子矩阵进行筛选，剔除各精度因子矩阵中大于3的元素，剩余元素所占比例、各精度因子原始矩阵均值如表3所示。

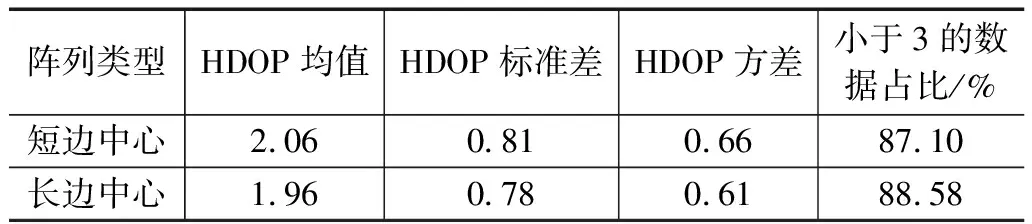
表3 两种阵列布置方式各参数比较

综上所述，当被测范围为正方形时，两种阵列布置方式完全一致，由表3两种阵列布置方式的精度因子计算结果来看，长边中心的三角阵列布置方式拥有更好的定位精度水平，因此最终选用长边中心的三角阵列布置作为最终应变传感阵列的布置方式。

2.2 采存模块设计

根据测量指标需求和测量流程分析以及测量任务分解，设计小型集成化的应变信号采集系统，并对其中信号放大、多路A/D同步采集等关键技术进行研究，同时为了满足研究过程中的实验测试需求，研究了多路数据同步存储来完成大量测试数据的获取。为了满足装甲内嵌式的使用需求，测量系统必须高度集成，且拥有足够的计算力支撑后续的数据解算。考虑以尽可能小的电路结构满足尽可能多的测量需求，测试系统要具备多通道同步采样的能力。针对多通道数据采集中采样起始时间不一致、时间同步性差等问题，结合高集成、小型化的设计需求，对测量电路系统进行功能性设计。系统需要具备采样率设置灵活且准确、15路信号同步启动采样以及数据的读取和计算等功能。系统硬件主要由三部分组成，分别为供电部分、传感放大部分和采样控制部分。系统结构框架如图13所示。

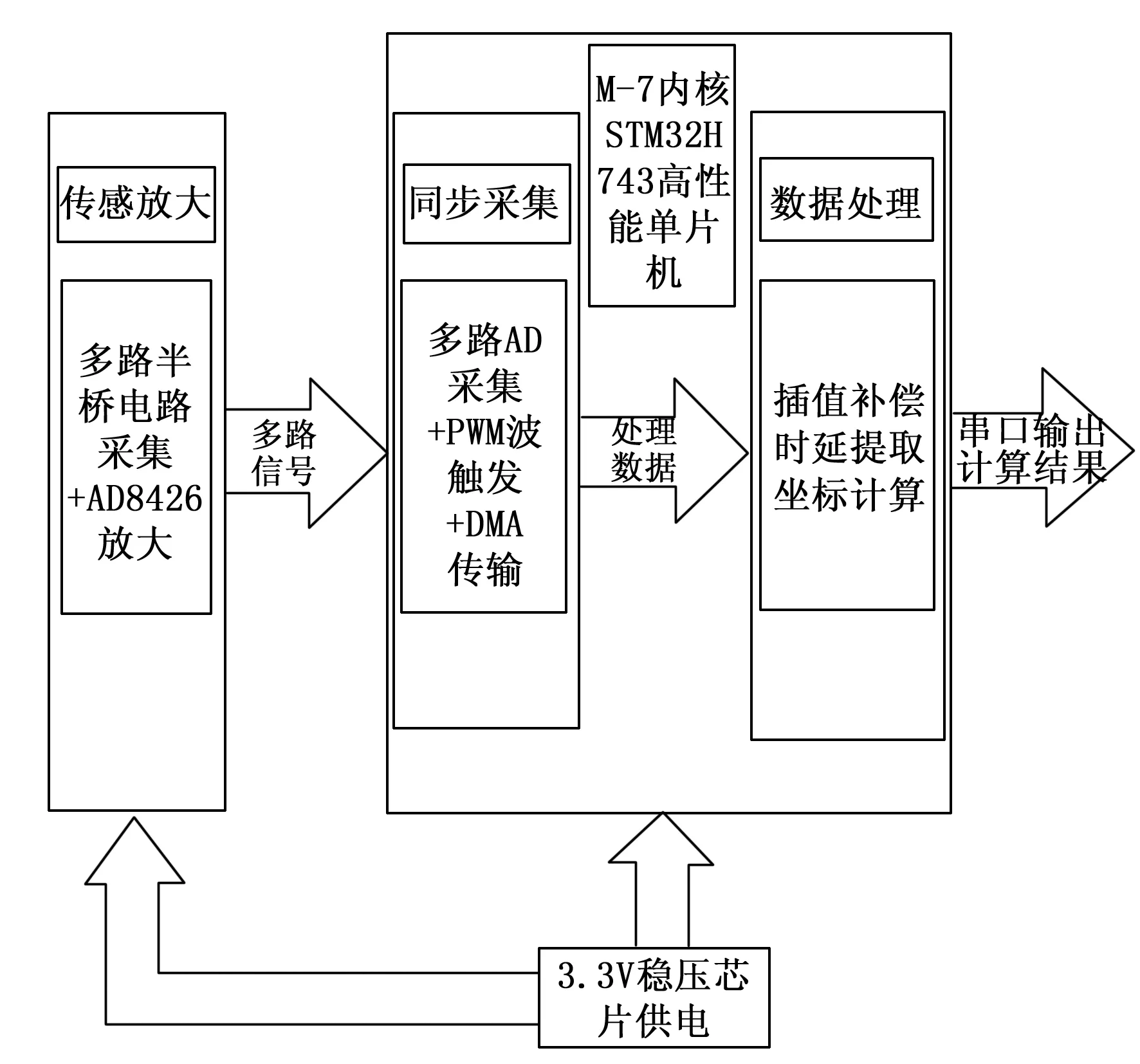
图13 系统总体框架

电阻应变片参与构成的半桥电路输出非常微弱，所以实际使用中需要将电桥输出信号进行放大。放大电路是每一个测量仪器必备的电路，它不仅可以将微弱信号无失真地放大至采集电路可接受的范围内，还可以将较大的信号进行衰减，以扩大信号输入范围，提高测量仪器的测量量程，扩展测量仪器的适用方向[12]。

应变传感放大部分由半桥电路和放大电路组成。

选择ADI公司的AD8426仪表放大器作为设计所用，结合芯片手册可知，AD8426每个通道的放大倍数G由一颗外部电阻RG来确定，单通道放大倍数G和对应通道的RG之间的关系由式(3)确定：

(3)

此时，AD8426的输出电压VO与输入电压V+I N、V-I N之间的关系由式(4)确定：

VO=G(V+I N-V-I N)+VREF

(4)

式中，VREF为测量通道的偏置电压。

本文选用的应变片为国内某公司生产的型号为BFH120-3AA的应变片，精度等级为A级，其灵敏度系数为2.0，应变片灵敏度系数Gf由下式给出：

(5)

式中，ΔR为应变片电阻变化量，R为应变片标称电阻值，单位均为Ω，ε为应变片产生的应变。结合式(2)可知，当桥路供电电压UE为3.3 V时有：

UL=3.3ε

(6)

此时电桥电路输出电压与应变片产生的应变为一次线性关系，根据我国2008年修订的电阻应变片标准《金属粘贴式电阻应变计》(GB/T13992-2010)，A级精度的金属应变片的应变极限为2%，则此时可知，在应变片的极限应变下，桥路输出电压最高为66 mV，而负责信号采样的STM32H743的内部ADC在供电电压为3.3 V的情况下，其ADC量程为0～3.3 V，为了保证在系统的测量范围能涵盖应变片的极限应变，本文确定的放大倍数为50倍。由式(2)～(3)可以计算得出此时所需要的RG的阻值为1 008 Ω。

本系统设计中，为了达到小型化、高集成的设计目标，要尽量减小电路规模，且高算力的需求也要求所选取的微处理器核心要有较高的主频来确保计算速度，同时要有丰富的外设能满足所测试需求。因此选用基于ARM-Cortex-M7内核的STM32H743IIT6MCU芯片(以下简称 H743)作为微处理器。其采用的M7处理器在采集数据的速度、精度以及可靠性上相较F4、F2系列处理器都有大幅度的提高[13-14]，为了满足小型化设计，缩小电路规模，本文没有采用专用ADC采集芯片，使用H743的内部ADC来进行A/D采样。STM32系列单片机作为单线程处理器，在同一时刻只能进行一项操作内容，在使用其进行多路同步采集时，如果通过常规软件触发来启动各ADC的采样，那各ADC启动必然有先后顺序，软件触发的时间差无法精确确定，且由于ADC3不具备耦合功能，此时ADC1、ADC2与ADC3的各个通道的采样会产生无法确定的时间差，无法保证各ADC采样结果时间轴的同步性。针对上述问题，考虑到H743的ADC支持硬件触发采样模式，系统通过使用内部高精度定时器来产生PWM波，使用其上升沿来触发ADC采样[15]。此时具体ADC采样率计算公式为：

(7)

式中，fSR为ADC采样率，单位Hz；fpsc为预分频器频率，单位Hz；psc为预分频系数；arr为自动重装载值。

H743的内部SRAM大小只有864 kB，而H743并非并行处理器，其核心为单线程处理器，如果采用定时器触发，DMA联动ADC扫描模式的方式，在通过定时器产生的PWM波来触发A/D转换后，DMA依次将所有转换结果搬运至内存，无论将DMA设置为循环模式还是单次模式，由于受到内部SRAM大小的限制，必然无法将所有测试数据都完整的保存下来。针对上述问题，考虑H743的内部DMA支持内存和外设的任意两两互联，本文通过将ADC配置为DMA传输模式，使用DMA传输完成中断在内部SRAM中建立两个32位数组作为缓冲区，通过“乒乓操作”实现数据的同步采集和存储，具体程序流程如图14所示。

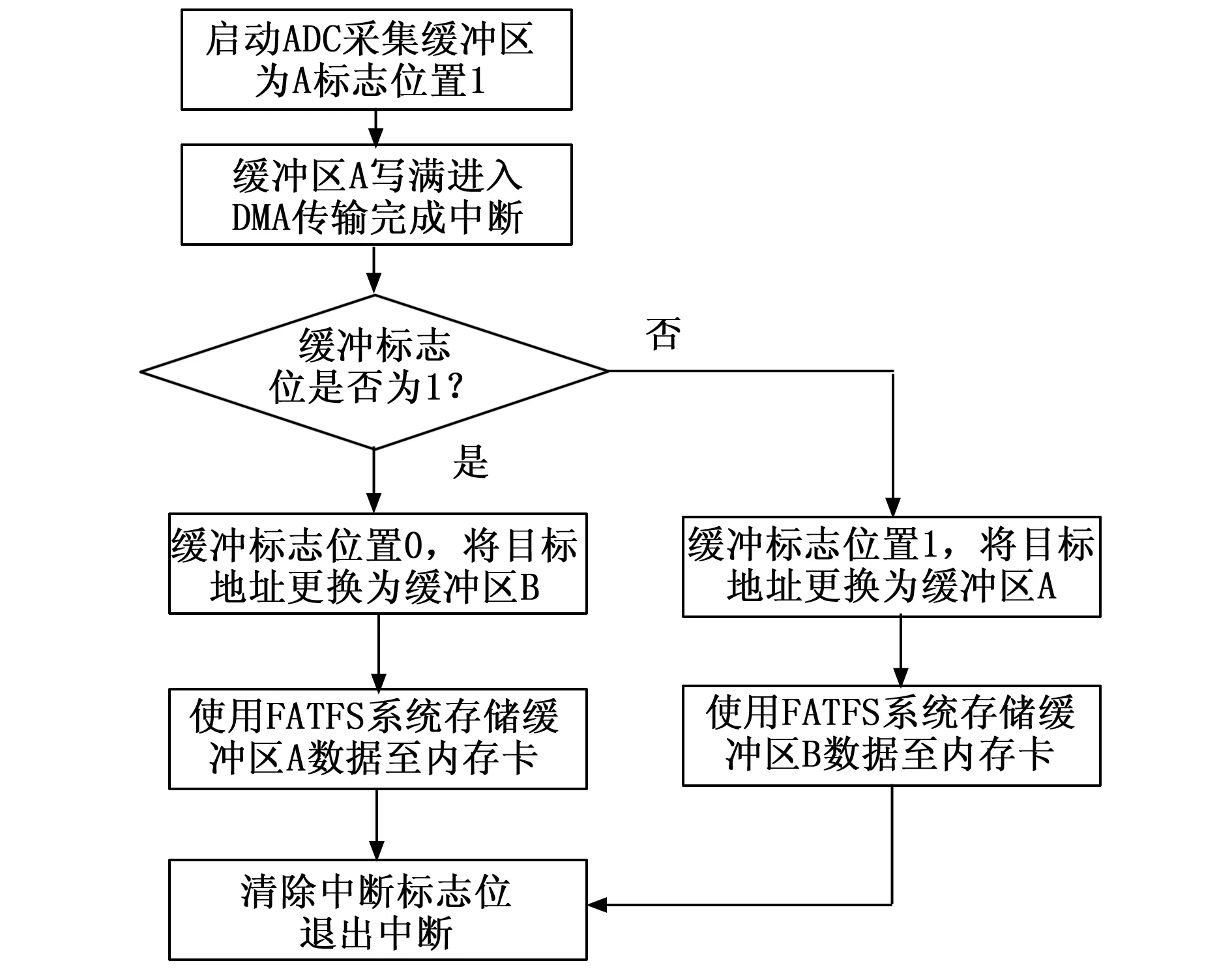
图14 DMA传输完成中断乒乓操作

3 系统算法设计

3.1 时差标定补偿算法设计

根据前文可知，在进行应变数据采集时必然存在单ADC不同通道的切换操作。在单ADC工作过程中，每一个ADC的常规采样序列内的不同通道间切换由电子开关完成，ADC通道切换时间难以从硬件层面来确定，同时对于单通道的采样结果而言，由于存在采样保持时间和转换时间，也难以从时间轴上给出确定的采样时间点，ADC多通道系统的TR组件和射频前端及其连接电缆，在模块设计和系统集成上都很难保证多通道的同步一致性[16]，导致难以确定前后通道间的采样时间差。

针对上述的单ADC多通道采集带来时间差无法确定的问题，设计了时间差标定算法：正弦波信号是一种最为常见的信号，是频率成分最为单一的信号，基于其时域特点和频率单一的特点，通过数学推导设计了如下标定办法。

首先设置好ADC采样率，设此时单通道采样周期为T，前后两通道时间差为τ，设前通道采样得到的正弦波信号为f1，后通道采样得到的正弦波信号为f2，两通道的采样时间差为τ2，令两通道对频率ω，幅值为A的同一正弦信号源进行采样，此时，对于两通道各自的第n个采样点处有：

f1(n)=Asin(ωnT)

(8)

f2(n)=Asin[ω(nT+τ2)]

(9)

令式(9)减去式(8)可得：

Δf(n)=f2(n)-f1(n)=Asin[ω(nT+τ2)]-sin(ωnT)

(10)

令使用三角函数诱导公式对式(10)进行推导可得：

Δf(n)=A[sin(ωnT)cos(ωτ2)+

cos(ωnT)sin(ωτ2)-sin(ωnT)]

(11)

单ADC在执行连续转换时，不同通道间的时间差都非常小，此时通过数学上等价无穷小的概念对式(11)进行推导简化。

在τ2非常小时，有：

sin(ωτ2)=ωτ2

(12)

cos(ωτ2)=1

(13)

将式(12)和式(13)代入到式(11)可得：

Δf(n)=Aωτ2cos(ωnT)

(14)

此时，Δf、A、ω、nT均为已知量，则有：

(15)

以上通过使用两通道对同一已知正弦波信号进行采样，再结合等价无穷小的概念，得到了第n个采样点处的两通道时间差。但是逐个计算得到的时间差值并不能作为对某一ADC在某个采样率模式下的两通道时间差常量，要对某一ADC的相邻通道采样时间差进行标定还需要大量数据的参与，此时需要通过使用Matlab曲线拟合工具完成对某一确定ADC的某个采样率模式下通道采样时间差的标定。

由式(14)可知，两通道采样结果之差是一个幅值为Aωτ2，频率为ω的余弦函数，在得到两通道的采样结果之差后，使用余弦模型进行拟合，得到的拟合函数的幅值参数就包含了此两通道的时间差信息。设拟合得到的幅值参数为A1，则此时有：

(16)

对于单ADC的多通道时间差进行补偿时，要对后通道的每一个采样点进行补偿，所以采用插值法对其进行补偿。分段线性插值法原理简单，运算速度快，但缺点在于节点处的导数不连续，导致插值函数失去光滑性[17-18]。三次样条插值法采用高次多项式来近似的得到离散数据的函数，光滑性更好，且对于待插值区间的大小要求较线性插值法低，同时有更多的数据点参与计算。其基本原理是通过将需要插值的区间分解成数个小区间，在每个小区间内构建三次方程并求解，再根据需要的自变量变化值得到插值点数值。根据三次样条插值法原理，本文设计了如下的插值补偿算法。

设ADC每个通道的采样产生的数据点个数均为n+1个，设ADC的后通道的第i个采样结果表示为(xiyi)，并且设ADC的采样周期为T，此时在时域图中有：

xi=0，T，2T，…，nT

(17)

将所有数据点分成n个区间，[(x0，x1)，(x1，x2)，…，(xn-1，xn)]，在每个区间中构建三次函数方程如下：

Si(X)=ai+bi(x-xi)+ci(x-xi)2+

di(x-xi)3，i=0，1，…，n-1

(18)

那么n个区间对应方程组如下：

(19)

易知，上述方程组同时满足条件S(xi)=yi，i=0，1，…，n。此时对于n+1个数据点而言，通过在每个区间内生成三次函数的方式，总共可以生成n个三次方程，每个三次方程都有4个未知系数，a，b，c，d，共计4n个未知系数。若要解得所有未知量的值，则最少需要4n个方程。

以下给出5个约束条件，在n个区间内构建4n个方程来解出所有的未知系数。

约束条件(1)：

所构建的n段三次函数曲线必须过所有已知数据点，即所有方程需满足：

Si(xi)=yi，i=0，1，…，n

(20)

此时已知数据点个数为n+1个，要让所有区间内三次函数均满足上式，可得到n个方程，具体如下：

yi=Si(xi)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3

(21)

式中，i=0，1，…，n-1。对于第n+1个数据点，通过其所在区间的三次函数给出单独方程：

Sn-1(xn)=yn

(22)

此时通过n段三次函数必须经过所有已知数据点的约束条件共计得到n+1个不同的方程。

约束条件(2)：

对于这n-1个数据点来讲，其各自前后区间内构建的三次函数值在该数据点处的函数值相等。则此时有：

Si(xi+1)=Si+1(xi+1)

(23)

式中，i=0，1，…，n-1。此时根据约束条件(2)可以得到n-1个不同的方程。

约束条件(3)：

其各自前后区间内构建的三次函数值在该数据点处的函数导数值相等。则此时有：

(24)

式中，i=0，1，…，n-1。此时根据约束条件(3)可以得到n-1个不同的方程。

约束条件(4)：

其各自前后区间内构建的三次函数在该数据点处的曲率值相等。则此时有：

(25)

式中，i=0，1，…，n-1。此时根据约束条件(4)可以得到n-1个方程。

约束条件(5)：

令第一个区间内和最后一个区间内所构建的三次函数的二阶导数分别在第一个原始数据点和最后一个原始数据点处的函数值为0。此时有：

(26)

至此得到一个方程数量为4n的方程组，将其以矩阵形式表示可得：

AX=B

(27)

式中，

在解得所有的未知系数后，便可得到符合要求的n个三次函数。此时设相邻两通道时间差为τ2，对于第i(i=1，2，…，n)个采样点处有：

ΔSi-1(xi-τ2)=a0+b0(xi-τ2-xi-1)+

c0(xi-τ2-xi-1)2+d0(xi-τ2-xi-1)3

(28)

式中，ΔSi-1(xi-τ2)为第i(i=1，2，…，n-1)个采样点进行采样时间差补偿后的采样值。

3.2 广义互相关时延估计算法设计

广义互相关是一种基于基本互相关时延估计算法而进一步提出的时延估计算法。理论上首先对两路测得信号进行预滤波处理，再对预滤波处理得到的输出信号求取其相关函数，即GCC (generalized cross correlation)函数，最后对GCC函数进行峰值检测，对应的时间值即为时延估计值。

在实际应用中，一般采取通过功率谱加权的方式来进行测量应用。将测得信号转换为功率谱，对功率谱进行加权，再通过傅里叶反变换转换为相关函数。

此时设权函数为：

W(f)=H1(f)×H2*(f)

(29)

其中：H1、H2为引入的前置滤波器，*表示共轭，由傅里叶变换和功率谱密度的关系，可以得到：

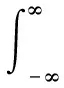
(30)

式中，G12(f)为输入信号的互谱密度，则此时可得两输入信号经过H1和H2滤波后的互功率谱密度为：

Gy1y2(f)=W(f)G12(f)

(31)

则两输入信号的广义互相关结果为：

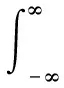
(32)

实际中，由于数据长度有限，无法得到理想的互功率谱密度，只能得到互功率谱密度的估计值，因此上式的估计式为：

(33)

当频率加权函数不同时，得到的互相关处理结果也不同，相位变换加权(PHAT)计算简便，在高信噪比时波动较小，峰值尖锐，低信噪比时也表现出较好的扛干扰性[19]。本文采用PHAT加权函数来进行广义互相关函数的求解。

3.3 TDOA-Taylor算法设计

TDOA即为基于到达时间差的定位算法。基于TDOA的定位模型从几何模型的角度也可称之为双曲线定位模型[20-21]，几何数学中，所有与两定点距离差值为一个定值的点的集合，是一个以两定点为焦点的双曲线。当定点数量超过两点时，多个双曲线的交集为唯一点。为了描述TDOA定位方法在装甲表面冲击定位中的应用，建立如下的简单模型。

在装甲表面冲击定位中，装甲板一般由均匀介质组成，为了方便解算冲击位置，将应变在装甲板中的传播速度视为不变常量。根据前文所设计的应变阵列布置方式，在一个长为A，宽为B的矩形装甲平面上布置一个长边中心的三角测量阵列，则此测量范围内的测量网络由三个测量节点和一个待定位点组成。

TDOA-Taylor算法是一种典型的递归算法，算法的主要思路是通过循环迭代运算不断地修正待定位点坐标的估计值，将待定位点坐标值逼近到允许误差范围之内。通过将装甲板中心点设为初始迭代值，利用初始迭代值在Taylor级数展开的同时进行加权最小二乘法估计[22]。接着求解冲击位置估计误差的局部最小二乘解，并对迭代值进行更新，将更新后的迭代值再进行下一次迭代，直到估计误差小于预设值为止。以下给出TDOA-Taylor解算算法的实际应用过程。

设待定位冲击点坐标为(x，y)，测量点坐标为(xi，yi)，装甲中心坐标为(x0，y0)，误差许可值为η，此时有：

(34)

将fi(x，y，xi，yi)在初始坐标(x0，y0)处进行泰勒展开，忽略展开的二阶以上分式可得：

fi(x，y，xi，yi)=fi(x0，y0，xi，yi)+

(35)

设：

(36)

将上式代入式(35)，并化为矩阵可得：

ψ=hi-Giδ

(37)

式中，ψ是误差矢量，

加权最小二乘法解得：

(38)

再进行第二次迭代运算时，可更新待测量点坐标值进行迭代运算。不断重复直到Δx+Δy<η时停止迭代运算。

4 实验结果及分析

为了验证系统的应变采集放大功能，使用一块半径为15 cm的圆形装甲样品板作为传感载体，在其表面边缘处一点正反粘贴两片应变片。使用霍普金森冲击试验台对装甲板进行冲击，使用测量系统进行采集测量冲击测量结果如图15所示，测量结果的频谱如图16所示。

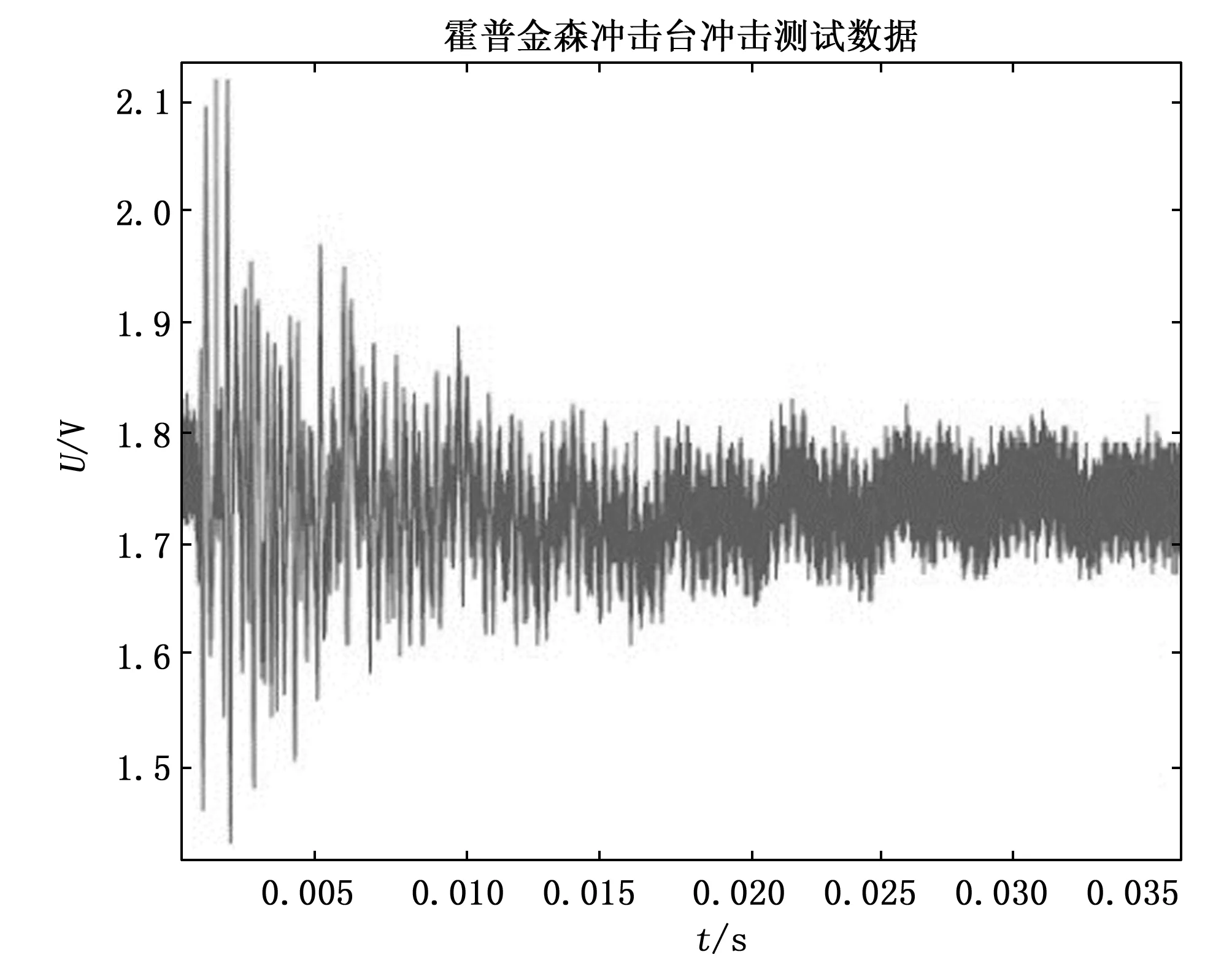
图15 霍普金森冲击台冲击测量结果

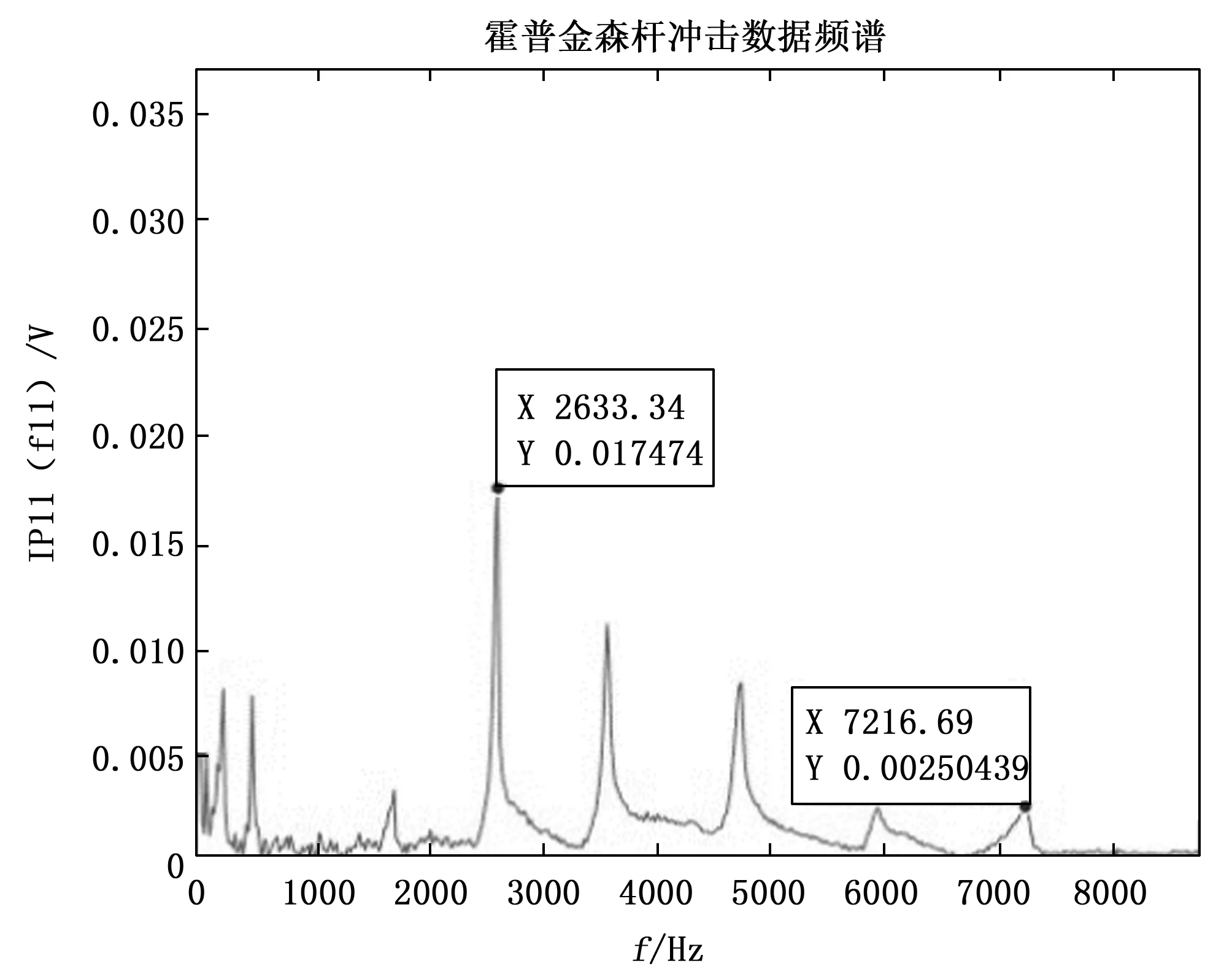
图16 冲击测量结果频谱

由图15可以看出，应变传感放大电路能够完成对冲击应变信号的传感和放大。根据图16可知，冲击产生的信号除直流分量以外最大频率分量出现在2 633 Hz处，最高频率的分量出现在7 216 Hz处。

为了验证广义互相关时延估计算法和TDOA-Taylor算法的可行性和性能，同时得到系统总体的测量精度和定位精度，设计了冲击定位实验，选用一片矩形装甲样品板作为传感载体，将空腔震膜结构焊接在其表面，并在其上按照长边中心的三角阵列布置方式布置应变传感阵列如图17所示。将装甲试样板用台钳固定，以P1处与同距点连线为纵轴，以同距点为原点确定各测量点坐标后对其进行杆状冲击并提取定位数据，杆状冲击方式如图18所示。测试中仅使用ADC1进行3通道采样，以P1点第一次冲击测试结

图17 冲击定位测试载体表面

图18 杆状冲击示意

果为例，其测试数据如图19所示。由广义互相关算法提取得到到达时差值再根据TDOA-Taylor算法来解算出测量到的冲击点坐标，结合与实际冲击点坐标做差值以确定冲击定位精度，测量结果如表4所示。

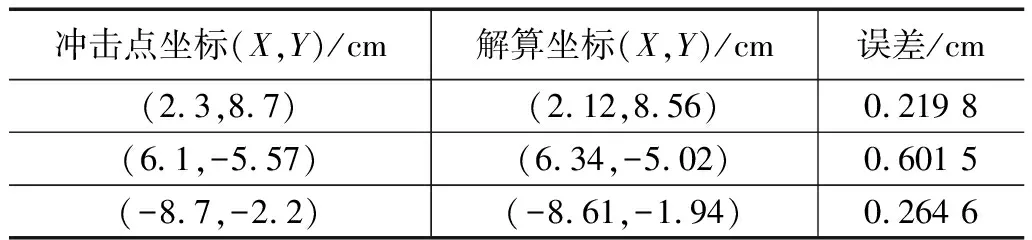
表4 坐标解算结果

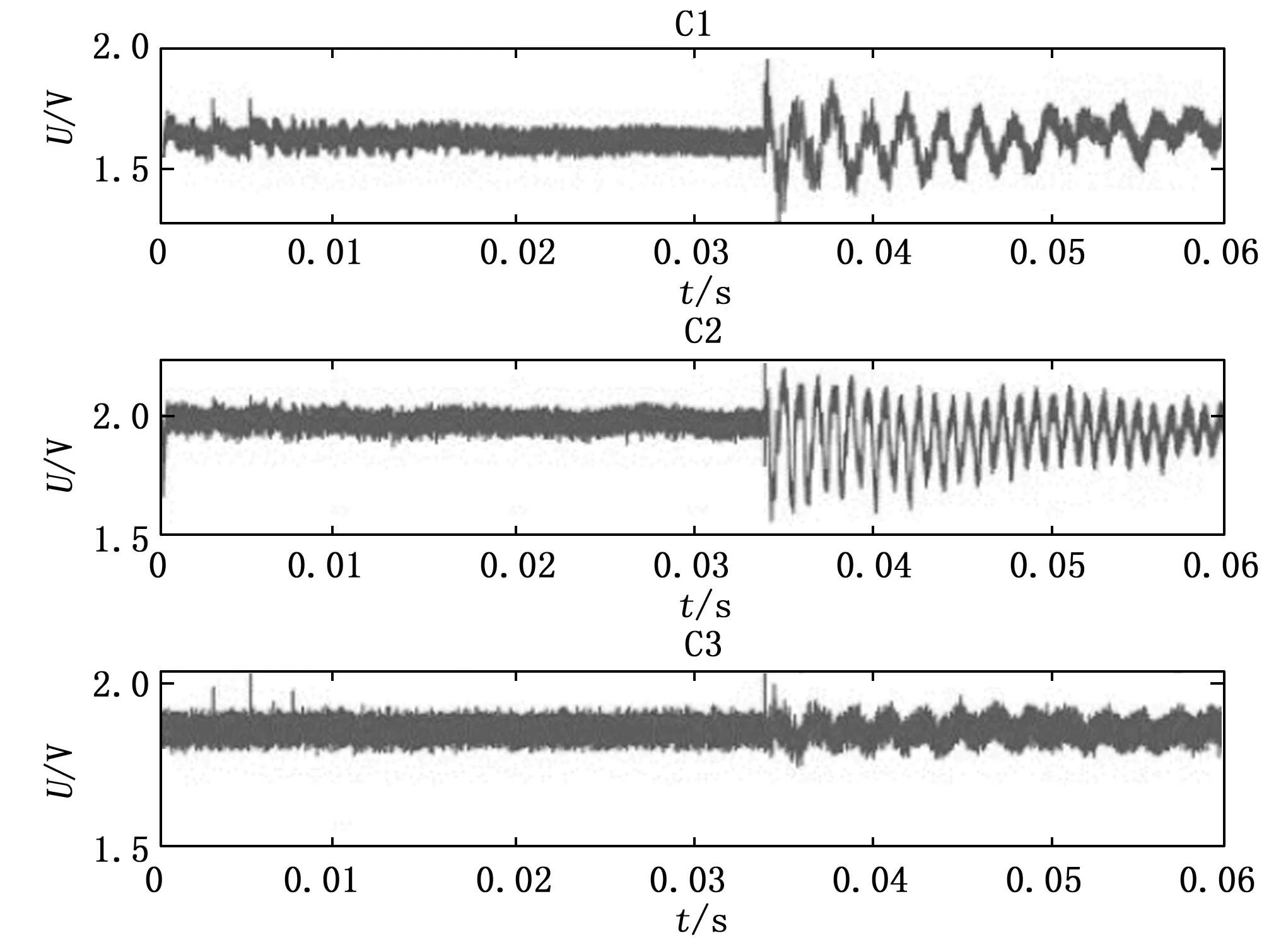
图19 P1点第一次冲击测量结果

由实际测量可知，时延估计平均精度为98.10%，定位误差小于 1 cm，能满足装甲表面冲击定位的需求。

5 结束语

针对装甲表面冲击定位问题，本文研究了基于智能化装甲的表面冲击定位技术。文章从定位方案设计开始分析，确定内嵌式应变片粘贴结构，设计阵列传感布置方式，研发定位硬件系统，设计时差标定方法和插值补偿算法，分析到达时差提取算法和定位算法，最终完成了装甲表面冲击定位技术的开发，验证了阵列布置、硬件系统、核心算法的可行性。为装甲单位定位外部装甲表面所受冲击提出了一条经济适用的技术路线，具有非常高的实际应用价值。所提出单ADC多通道采样的时差标定算法和事后插值补偿算法，虽然有效降低了不同通道的采样时间差，但是时差标定算法仍处于事前标定阶段，有必要对时差自标定方法开展研究与设计，进一步提高自动化水平。