基于神经网络PID的多轮轮毂电机协调控制研究

苏清源

(黑龙江工程学院 汽车与交通工程学院，哈尔滨 150050)

0 引言

在新能源迅速发展的背景下，轮毂式电动汽车已经成为汽车发展的重要方向。轮毂电机技术能够将动力、传动和刹车技术整合到轮毂中，降低车身的重量，增加车身的空间[1]。在工程实践中，通常将轮毂电机按其转子的结构形态分为不同的类型。为了降低多轮轮毂之间的运行偏差对驱动效果产生的影响，提出多轮轮毂电机协调控制方法[2]。现有的协调控制原理可以分为并联同步控制和主从控制两种。其中文献[3]提出了基于新型死区补偿的电机协调控制方法，该方法以并联同步作为控制原理为基础，分析了死区时间、开关等元器件的非线性死区效应问题，确定相关的影响因素，通过建立死区扰动电压观测器并与线性补偿法相结合的方式实现相关的死区补偿，以此实现电机协调控制。文献[4]提出了基于模型预测控制的电机协调控制方法。以并联同步作为控制原理为基础设计了电机协调控制器，该控制器由上层控制器和下层控制器两个主要部分组成。上层控制器设计了基于拉盖尔函数的模型预测控制器，综合分析保证DDEV稳定性所需的轮毂电机转矩约束条件，实现轮毂电机最优转矩分配，从而达到电机协调控制的目标。文献[5]提出了基于超扭曲非奇异滑模的电机协调控制方法，主要以主从控制为运行原理为基础，采用偏差耦合的电同步控制方式，对多电机转角误差进行补偿，利用新型非奇异快速终端滑模函数设计相关的控制器，从而达到电机协同控制的目标。在实际的应用过程中，并联同步控制具有起动、停机等特性，但由于整个系统具有开环的特性，因此，在运行中如果有一个电动机被干扰，就会使各电动机发生同步偏移，使其同步性能变差。而主从控制可以对主电机施加的任何速度指令和负荷干扰进行反应，但对来自电机的干扰不会反馈给主电机。在工业生产中，由于负荷的改变，无法保证电动机的同步精度。为了解决上述传统电机协调控制方法存在的问题，引入神经网络PID算法。

PID控制算法在工业领域应用得十分普遍，其主要是由比例、积分和差分三部分构成，测量时比较受控变量的真实值与期待值，以此修正系统的响应。神经网络是从联结主义观点、仿生学角度出发进行模拟的一个模型，可以模拟动物的行为特性，从而实现分布式的并行信息处理。该网络依赖于系统自身的复杂性，通过调节大量的节点间的联系来实现对数据的处理，同时还具备自学习和自适应的功能。将PID和神经网络整合起来，并将其应用到多轮轮毂电机协调控制方法的优化工作中，以此提升多轮轮毂电机的协调控制效果。

1 多轮轮毂电机协调控制方法

多轮轮毂电机协调控制方法以多轮轮毂电机上的组成元素为控制对象，利用神经网络PID算法优化设计电机的协调控制器，并生成能够作用在多轮轮毂电机上的协调控制指令，最终分别从力矩、转矩、速度等方面，实现对多轮轮毂电机的协调控制，最大程度地保证电机运行参数同步。

1.1 构建多轮轮毂电机数学模型

多轮轮毂电机的本质是永磁同步电机，从组成结构上来看，多轮轮毂电机内部主要包括：电动机本体、电子开关线路、逆变器等，通过多轮轮毂电机转子磁路的设计，使得空气间隙和感应电动势都是梯形波形，三相全桥转换电路的驱动是120°的两两接通。在三相电压型逆变器中，采用功率电子元件是最理想的设备，而不需要考虑电枢反应对空气间隙磁场的影响[2]。根据多轮轮毂电机的结构组成，考虑元件之间的连接方式，得出多轮轮毂电机的等效电路模型，如图1所示。

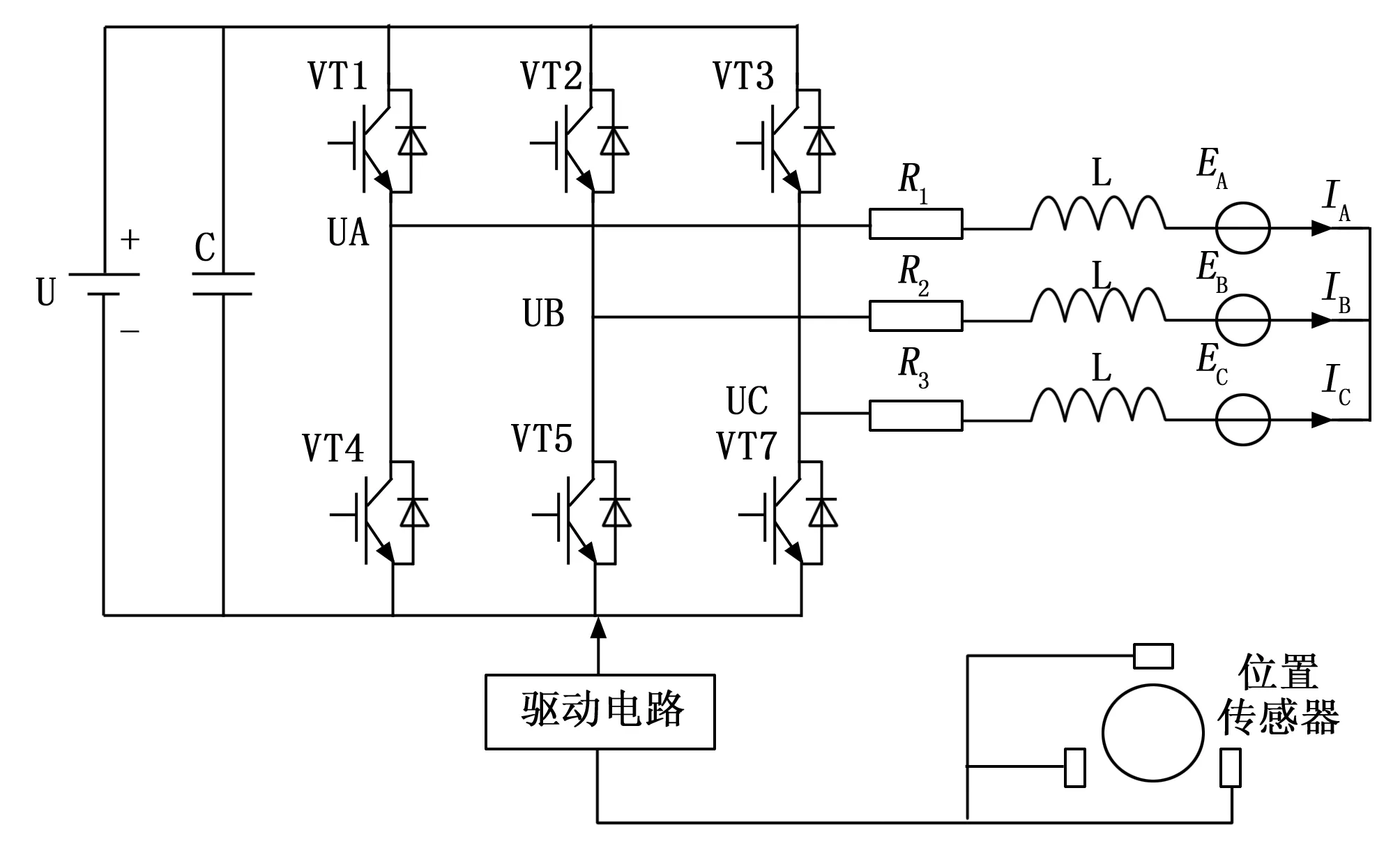
图1 多轮轮毂电机等效电路模型图

在电机学理论的支持下，多轮轮毂电机三相绕组的电压平衡可用公式表示为：

(1)

式(1)中，UA、UB和UC为多轮轮毂电机的三相定子电压，IA、IB和IC对应的是三相电流，R为绕组电阻，L和M为三相绕组的自感和互感，而变量EA、EB和EC分别表示的是三相感应电动势，参数ψ为微分算子，该参数的具体取值可以表示为：

(2)

式(2)中，t为时间，d为微分算子符号。考虑到实际电机工作的动态响应特性，多轮轮毂电机的电磁转矩、机械运动可以用公式表示为：

(3)

式(3)中，Z和F为电磁转矩和负载转矩，θ和ω为机械角速度和转子角速度，J为转子转动惯量，κf为黏滞摩擦系数。将上述运行原理公式与多轮轮毂电机组成结构以及等效电路进行融合处理，得出多轮轮毂电机数学模型的构建结果。

1.2 实时采集多轮轮毂电机运行参数

根据多轮轮毂电机的协调控制原理，对电机的实时运行参数进行采集，从而为电机协调控制量的计算提供数据支持[4]。待采集的多轮轮毂电机运行参数具体包括：电机转速、多轮位置、轮毂力矩等，以电机转速运行参数为例，采用周期法对其进行采集，具体的采集过程如图2所示。

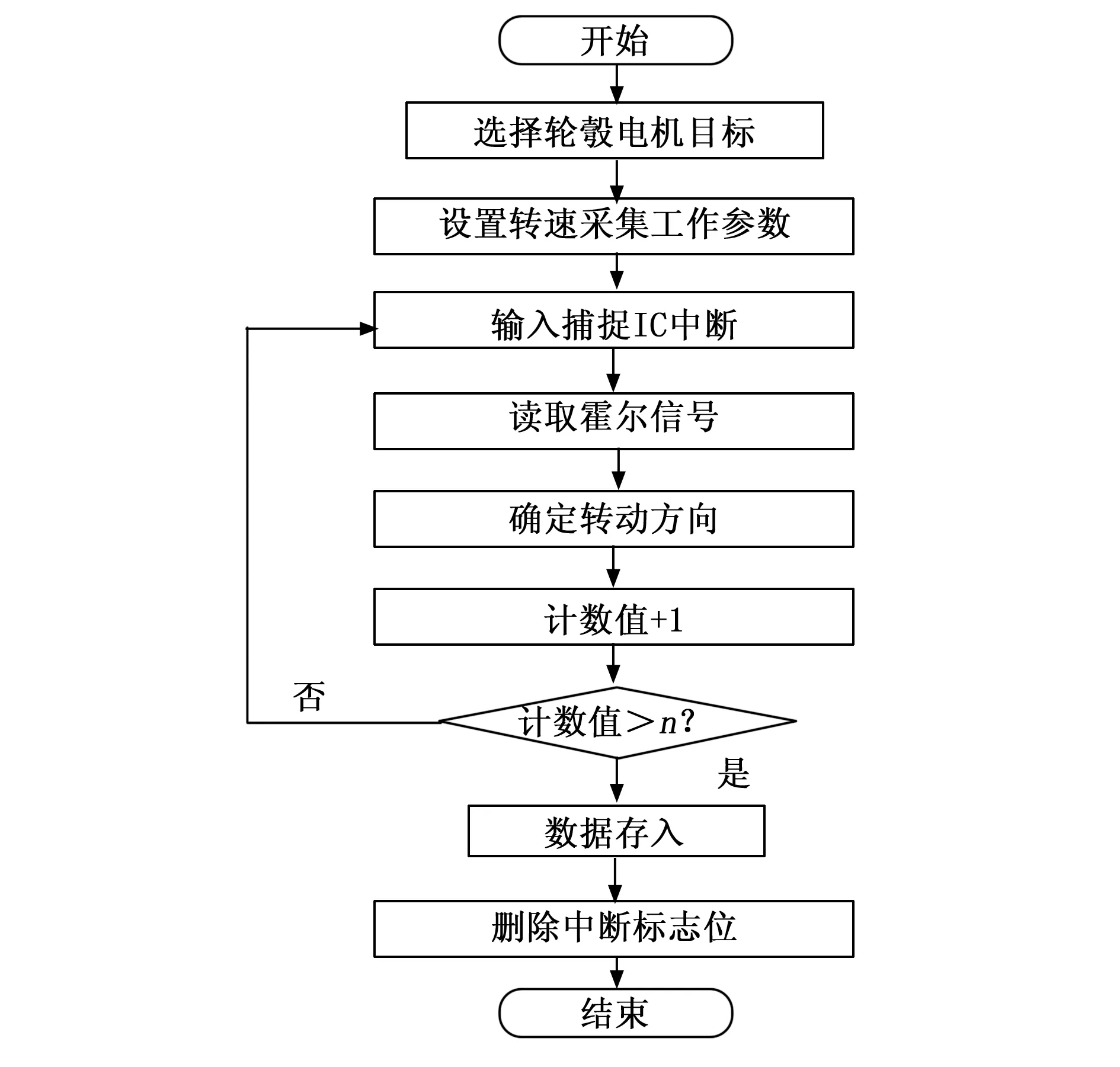
图2 多轮轮毂电机转速参数实时采集流程图

多轮轮毂电机转速参数采集使用周期法的主要运行原理是：利用霍尔信号中的两个脉冲信号之间的时间间隔来计算转速，利用高频时钟脉冲进行计数得出采集结果[5]。根据上述数据采集原理，可以得出多轮轮毂电机转速参数的采集结果为：

(4)

式(4)中，f为运行参数采集程序中定时器的输入时钟频率，Nele和Npulse分别为电机的极对数和时钟脉冲个数[6]。在此基础上，利用采集程序，可以得出多轮轮毂电机所有运行参数的实时采集结果。为了保证多轮轮毂电机运行参数的采集质量，需要对初始采集的运行参数数据进行预处理，预处理由卡尔曼滤波和归一化两个步骤组成，其中初始采集数据卡尔曼滤波增益处理结果可以用公式表示为：

xwave(t)=χG(χG·x(t)+Q)-1

(5)

式(5)中，χ为多轮轮毂电机运行参数初始值的方差阵，G为电机的观测状态矩阵，x(t)为运行参数的初始采集数据，Q为初始采集数据中的噪声部分[7]。在此基础上，利用式(6)对运行参数进行归一化处理。

(6)

式(6)中，xmax和xmin分别为运行参数采集集合的最大值和最小值，通过数据的归一化处理能够降低初始采集数据的异构程度[8]。

1.3 多轮轮毂电机协调控制

1.3.1 计算多轮轮毂电机协调控制量

根据多轮轮毂电机实时运行数据的采集与处理结果，设置电机的协调控制目标，设置的控制目标可以是轮毂电机任意轮的实际运行参数，也可以是其他固定值。以第i个轮作为控制目标，则多轮轮毂电机中任意轮j协调控制量的计算公式如下：

Δx=xi-xj

(7)

式(7)中，xi和xj分别为电机第i和j个轮的实际运行参数，根据结果的正负情况可以确定电机的协调控制方向[9]。若多轮轮毂电机协调控制目标为输入的固定值，则需要将其直接赋值给任意一个运行轮，在此基础上，按照上述步骤得出协调控制量的计算结果。

1.3.2 神经网络PID协调控制器

多轮轮毂电机协调控制的优化设计原理是在传统PID控制器的基础上，引入神经网络运行元件，并对PID控制元件与神经网络运行元件进行耦合处理。优化设计神经网络PID协调控制器的基本结构如图3所示。

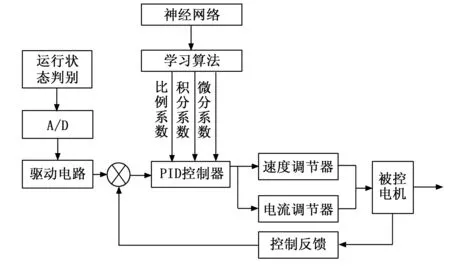
图3 神经网络PID协调控制器结构图

神经网络参数包括：比例、积分和微分参数[10]。将输出结果赋值给PID控制器的运行参数，并保证该参数具有可调性，根据神经网络本身的知识和权重的调节，使其达到最佳的控制效果[11]。为了降低外界干扰对控制器产生的影响，在协调控制器内部加设一个隔离变压器元件，该元件在协调控制器中的接入方式如图4所示。

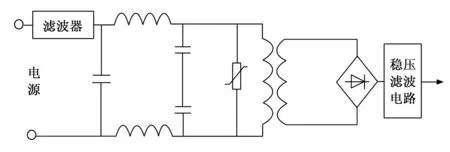
图4 隔离变压器元件的连接示意图

加设隔离变压器的原边和副边之间的漏抗很低，使得外来的干扰不会通过原边绕组流入到副边，进一步减小了外界的干扰[12]。在选用隔离变压器时，应选择合适的接入位置，并适当地解决屏蔽接地问题，使它与地面尽可能形成大范围的连接，并依据控制器的具体接地情况采取相应的接地方式。

1.3.3 利用神经网络PID算法生成轮毂电机协调控制指令

在神经网络PID协调控制器的支持下，生成相应的控制指令[13]。在控制指令的生成过程中，首先利用神经网络算法对PID控制程序中的运行参数进行整定，神经网络由多个神经元组成，每个神经元的状态可以用公式表示为：

(8)

式(8)中，si和sj为神经网络中第i和j个神经元，ϖij为神经元的连接强度，δi为阈值，nneuron为神经网络中包含的神经元数量，fStep为阶跃函数。通过多个神经元的连接，完成神经网络的构建，根据神经元类型与参数的不同，可以将神经网络分为多个结构，采用前向学习与反向学习相结合的方向，确定PID控制程序中各个参数的具体取值[14]。以多轮轮毂电机实时运行参数的采集结果为输入项，将其标记为sin-k(i)，其中k为输入层序号。将输入层的输出结果作为隐含层的输入值，隐含层各个神经元的状态可以被划分为比例、积分和微分三种类型，也就是PID控制程序的三个参数，设置神经元状态函数的取值区间为[-1，1]，则经过隐含层的训练，其输出结果为：

(9)

式(9)中，sImplicit-proportion、sImplicit-integral和sImplicit-differential分别为比例、积分和微分系数的求解结果[15]。式(9)的计算结果即为神经网络中隐含层的输出结果，将其代入到式(10)中，可以得出神经网络前向学习的训练结果，在输出层中直接输出。

(10)

式(10)中，nlayer为神经网络中的层级数量，ϖImplicit-out为隐含层与输出层的连接权值。神经网络反向学习的目的是调整各层之间的权重值，从而得出最优化的输出结果，以输入层与隐含层之间的权值为例，其迭代调整过程可以用公式表示为：

ϖin-Implicit(nd+1)=ϖin-Implicit(nd)-

(11)

式(11)中，nd和nControls分别为迭代次数和控制参数数量，β为学习步长，s0(i)为神经网络的给定值[16]。按照上述方式可以得出隐含层与输出层权重的迭代更新结果，在实际执行过程中设置最大迭代次数为终止条件，在满足终止条件前反复执行前向与反向学习操作，最终输出结果即为PID控制程序的整定结果，将整定后的参数代入到图5所示的PID控制程序中。

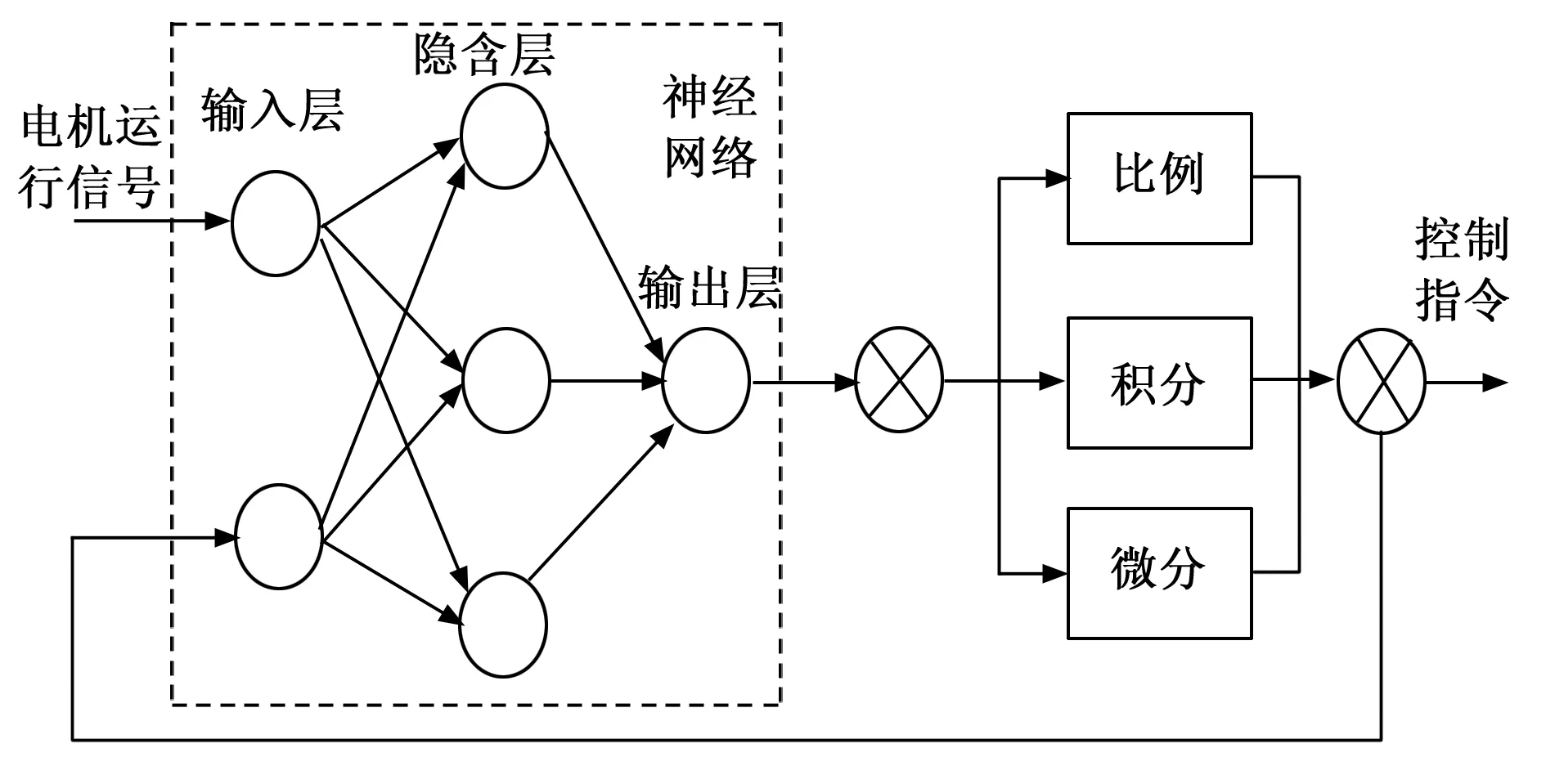
图5 PID控制逻辑原理图

根据图5所示的PID控制逻辑原理，得出多轮轮毂电机的协调控制指令为：

r(t)=sImplicit-proportion

(12)

式(12)中，e(t)为t时刻的控制偏差值。通过相关参数的动态更新，得出轮毂电机协调控制指令的实时生成结果，并直接作用在多轮轮毂电机上。

1.3.4 实现多轮轮毂电机协调控制

在神经网络PID算法生成多轮轮毂电机协调控制指令的驱动下，采用并行控制的方式，即每个电机都能够接收来自同一个单元的指令，从转矩、速度、稳定性等各方面执行协调控制指令[17]。要满足电动汽车的动力性要求，首先需要输入各轮的转矩必须满足需求转矩，其条件如下所示：

(13)

式(13)中，φdemand为转矩需求值，φfl、φfr、φrl和φrr为左前轮、右前轮、左后轮、右后轮的转矩[18]。多轮轮毂电机速度主要通过调节电枢端电压进行控制，这种方法能平稳地改变施加在电机端上的电压，使电机得到平稳的速度，达到无级调速。同理也可以实现对多轮轮毂电机多个运行参数的控制，从而达到多轮轮毂电机平稳运行的目的。

2 控制效果测试实验分析

测试实验的主要目的是验证优化设计的基于神经网络PID的多轮轮毂电机协调控制方法的控制效果，判断该控制方法是否可以达到预期效果，并投入到电动汽车的实际生产与行驶工作中。

2.1 选择多轮轮毂电机控制对象

实验选择KC115M623型号的多轮轮毂电机作为研究对象，该电机属于内转子式轮毂电机，其最高转速能够达到1 000 r/min以上，电机内部设计了减速装置，具有较高的功率密度[19]。从结构上来看，轮毂电机控制对象由6个轮组成，总成重量为55 kg，除传感器设备外，电机中还包含定子、转子、制动装置以及轮毂轴承等元件。电机的最大功率为40 kW，输出扭矩能够达到800 N·m。在开始实验之前，首先需要对选择的多轮轮毂电机设备进行调整，判断该设备是否能够正常运行，并根据控制指令调整相应的运行参数，保证控制对象的可操作性。

2.2 配置协调控制方法测试环境与实验工况

组建SERCOS光纤链路环网，对驱动器分配ISERCOS链路环网中的地址，设置上位机与控制器之间的通信链路。选择RSLogix5000编程软件，对优化设计的基于神经网络PID的多轮轮毂电机协调控制方法进行编程，并在运行软件中对硬件组态进行整合，完成实验环境的构建[20]。为测试优化设计方法是否能够满足多轮轮毂电机多种运行工况的协调控制要求，分别设置空载和负载两种实验工况，其中空载工况就是未将多轮轮毂电机装入电动汽车中，直接与供电电源、上位机以及控制器相连。而负载工况，也就是上车实验，将控制对象接入到实际车辆环境中，具体的配置方式如图6所示。

图6 多轮轮毂电机负载工况配置示意图

实验选择负载电动汽车的基本尺寸是2 500*1 600*1 400(mm3)，整车整备质量为600 kg，采用通风盘式+电机制动类型的制动器。建立一个多轮轮毂电机监测程序，并与控制对象相连，监测电机的转速、转矩等参数。

2.3 生成多轮轮毂电机协调控制任务

为保证实验结果的可信度，针对空载和负载两个工况，设置多组电机协调控制任务，其中部分任务的生成情况，如表1所示。

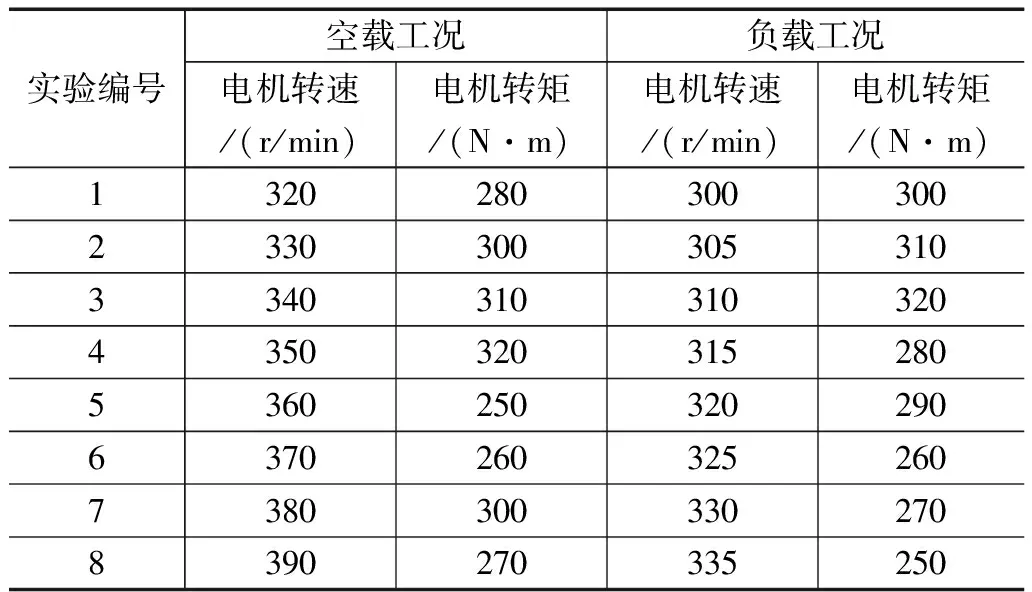
表1 多轮轮毂电机协调控制任务生成表

为保证实验变量的唯一性，负载工况下多轮轮毂电机的负载量均为电动汽车重量。

2.4 输入神经网络PID算法运行参数

由于优化设计多轮轮毂电机协调控制方法应用了神经网络PID算法，因此需要设置相关参数进行测试。PID控制算法中，设置比例系数的初始值为0.5，积分和微分系数均为0.1，神经网络算法中，设置输入节点和输出节点数量与多轮轮毂电机的轮一致，隐含层节点数为15个，各层之间的连接权重均为0.5，学习速率为0.9，最大迭代次数为200。将上述参数的初始值输入到多轮轮毂电机协调控制方法的运行程序中。

2.5 描述协调控制方法实现与测试过程

将优化设计的神经网络PID控制器安装到电机设备中，在开始实验之前，分别从运行状态和适配度两个方面进行调试。在运行状态的调试过程中，主要测试控制器是否能够根据输入的数据信号生成相应的控制指令，而适配度测试则是判定控制器是否能够成功接收多轮轮毂电机的运行信号、生成的控制指令是否能够成功驱动多轮轮毂电机。若存在调试不成功的情况，则需要对控制器设备进行重新连接，若调制成功则可以执行实验的下一步操作。在配置好的实验环境下，根据电机工况的设置情况，将电机调整到工作状态，并控制初始状态下电机的运行数据。将生成的多轮轮毂电机协调控制任务逐一输入到神经网络PID协调控制器中，根据当前电机的实际运行状态，得出协调控制量与控制指令，通过控制器硬件设备，实现对多轮轮毂电机的协调控制任务，优化设计方法执行1号控制任务的输出结果如图7所示。

图7 多轮轮毂电机协调控制界面

按照上述方式可以得出所有控制任务的执行结果。在空载工况实验执行完毕后，将电机移动至电动汽车的指定位置，同时启动电动汽车和电机，按照上述流程得出负载工况下的测试结果。实验设置传统的基于新型死区补偿的电机协调控制方法和基于模型预测控制的电机协调控制方法作为对比方法，在相同的实验环境下进行方法开发，并在对比控制方法下执行数据。

2.6 设置实验对比方法和测试指标

将文献[3]所提出的基于新型死区补偿的电机协调控制方法、文献[4]所提出的基于模型预测控制的电机协调控制方法、文献[5]所提出的基于超扭曲非奇异滑模的电机协调控制方法作为实验对比方法。

文献[3]方法所采用的MATLAB/Simulink仿真软件以id=0闭环矢量控制为基础，搭建了相关的控制协调仿真模型，所用算法为变步长Ode23tb算法，仿真时间为0.3 s，直流母线电压为540 V，PWM开关频率为10 kHz，开关周期Ts=0.000 1 s，逆变器死区时间设置为6×10-5s。文献[4]方法搭建了基于Simulink的控制系统仿真平台，采样周期Ts=0.005 s，仿真时间为10 s，步长参数为1×10-2s，仿真工具为ode45，仿真停止时间为1 min。

根据协调控制任务的设置情况，分别从转速、转矩和平衡度三个方面设置测试指标，通过测试指标反映协调控制方法的控制效果。设置转速与转矩控制误差的数值结果为：

(14)

式(14)中，υspeed，i、υtarget，i、φi和φtarget，i分别为电机第i个轮毂转速和转矩的实际值与控制目标值，nround为电机中的轮毂数量，在转速的实际测试中需要考虑定子和转子两个部分。另外平衡度控制效果的测试结果可以用公式表示为：

(15)

式(15)中，υspeed，j和φspeed，j为第j个轮毂的转速和转矩。最终通过计算得出转速和转矩的控制误差越小、电机平衡度越高，由此可以证明对应方法的控制效果越优。

2.7 协调控制效果测试实验结果与分析

在文献[3]方法、文献[4]方法以及本文方法的作用下，分别对空载工况多轮轮毂电机的实际运行数据进行采集，得出协调控制效果的测试结果，如图8所示。

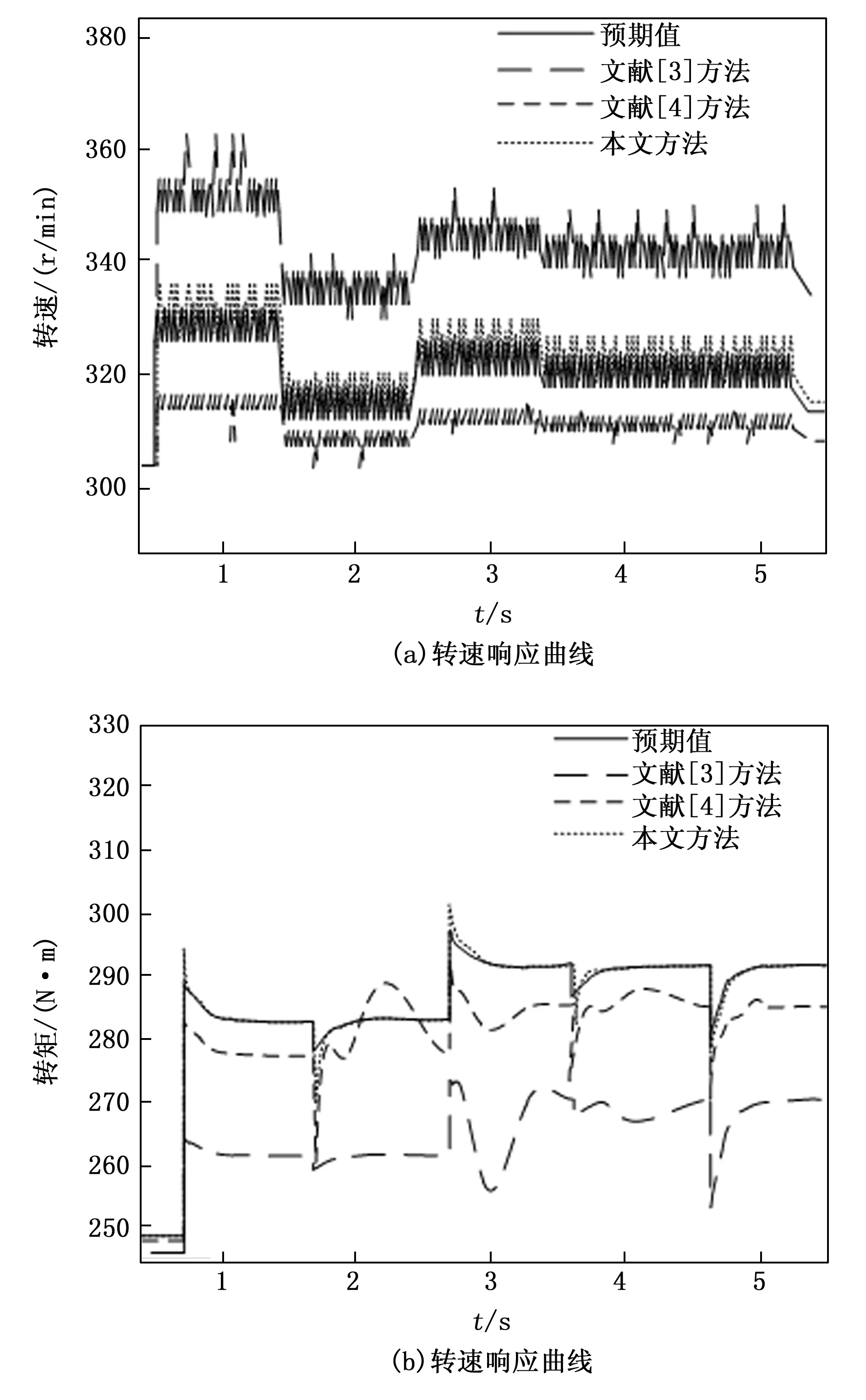
图8 空载工况下多轮轮毂电机转速、转矩控制测试结果

从图8中可以看出，与传统协同控制方法相比，在本文方法的控制下，多轮轮毂电机的实际转速与转矩更接近控制目标，且转速与转矩的响应曲线与控制目标基本一致。将图8中的数据代入到公式(14)中，计算得出三种方法的转速控制误差的平均值分别为28.6 r/min、19.3 r/min和2.7 r/min，平均转矩控制误差分别为16.4 N·m、7.1 N·m和5.2 N·m。同理可以得出负载工况下多轮轮毂电机转速与转矩的协调控制结果，如表2所示。

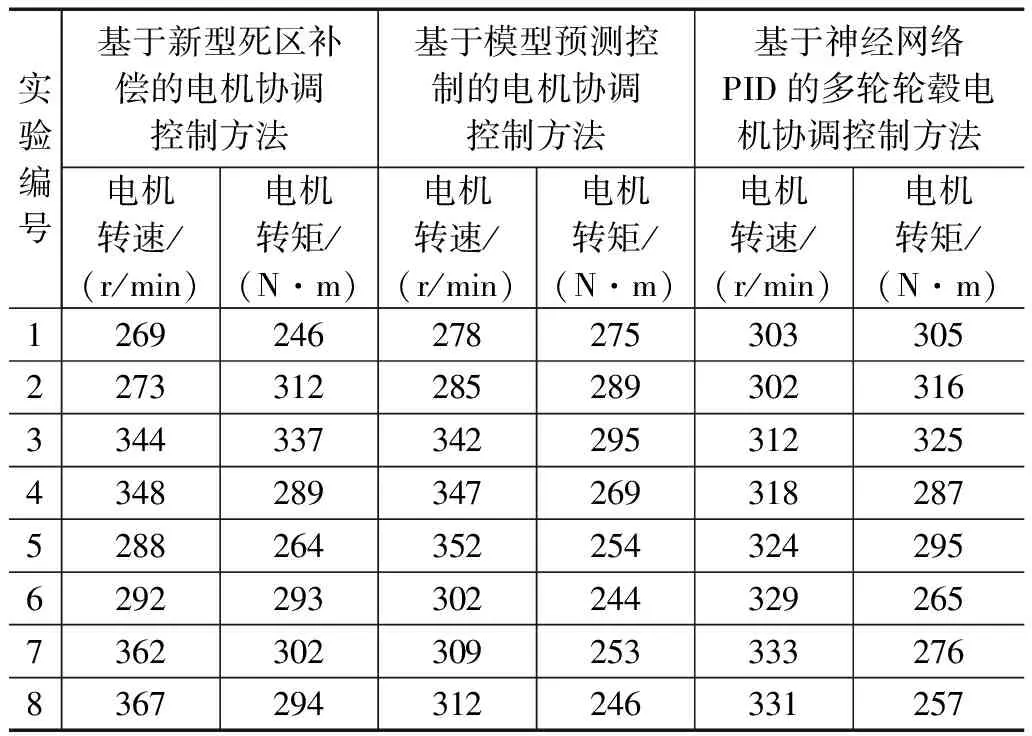
表2 负载工况下电机转速、转矩控制测试数据表

将表2中的数据代入到公式(14)中，计算得出对比方法的平均转速控制误差分别为32.4 r/min和25.6 r/min，转矩控制误差的平均值为27.1 N·m、19.4 N·m，优化设计控制方法作用下，电机转速和转矩的平均误差分别为3.3 r/min和5.8 N·m。另外，统计多轮轮毂电机中各轮的运行参数，通过公式(15)的计算，得出不同协调控制方法下，多轮轮毂电机平衡度的测试对比结果，如图9所示。

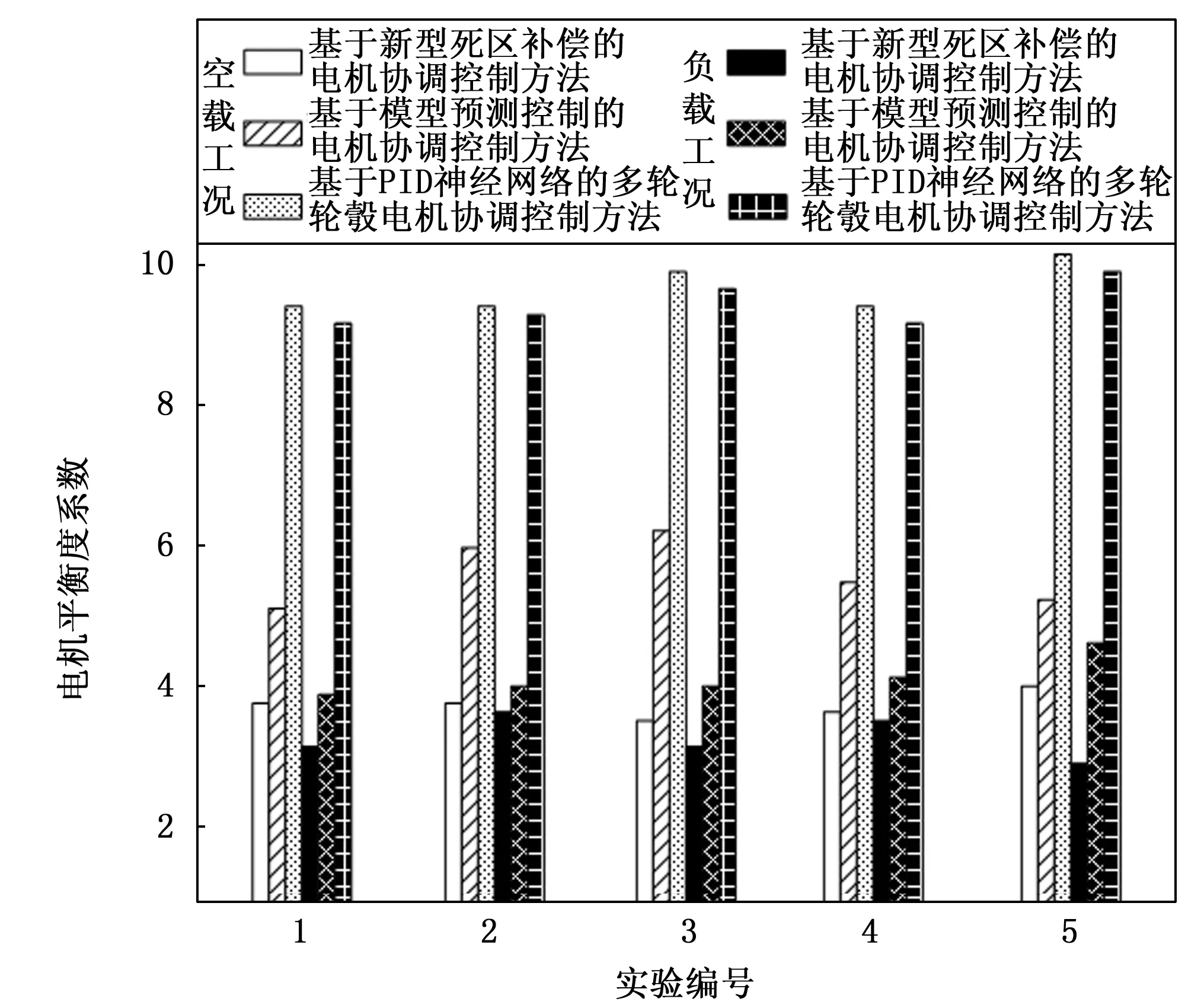
图9 多轮轮毂电机平衡度测试对比结果

从图9中可以直观地看出，在多轮轮毂电机的运行过程中，利用优化设计协调控制方法能够有效提高电机的运行平衡度，从而保证电机的平稳运行。

3 结束语

由于轮毂电机中多轮运行参数的非线性特征，导致多轮轮毂电机存在运行性能差的问题，多轮轮毂电机协调控制方法对于电机的运行性能以及应用价值具有重要的决定作用，通过应用神经网络PID算法，有效提升了协调控制效果。从实验结果中可以看出，优化设计方法能够适应电机的两种运行工况，且在空载状态下的控制效果更佳。然而在此次测试实验中，负载工况只设置了一种条件，因此得出的实验结果存在一定的局限性，针对这一问题还需要在今后的研究工作中进一步补充。