电磁轨道发射装置电磁热力强耦合计算及分析
赵赛,祝丽花,郝建英,闫荣格,杨庆新
(1.天津工业大学 电气工程学院,天津 300387;2.天津理工大学 电气工程与自动化学院,天津 300382;3.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130)
电磁轨道发射装置将电磁能转化为电枢运动所需要的动能,推动电枢在轨道中加速以获得超高发射速度,相比于传统的发射方式,因其弹丸初速可控性好、获得初速高、发射效率高等优势,具有十分广阔的应用前景[1-3]。电磁轨道发射装置涉及电磁、结构、温度等多物理场强耦合的复杂问题,由于运动工况下的强耦合时变特性,使得工程应用中难以准确得到基于多物理场强耦合的理论解析模型[4-6]。因此,研究电磁轨道发射装置电磁热力多物理场强耦合计算及分析方法是十分重要的。
针对电磁轨道发射装置的电磁热力多物理场强耦合计算问题,国内外对建立强耦合计算模型进行了广泛的研究,Kuo-Ta Heish等开发了具备多物理场数值计算能力的EMAP3D软件,采用有限元方法和边界元方法的混合算法,通过建立电磁轨道发射器的多物理场瞬态耦合模型,对高速滑动电接触的问题进行了深入研究,同时对电枢和轨道的瞬态电磁力和温度分布特性进行了数值计算[7-9]。Shetsov等采用加权残值有限元和边界元相结合的方法,编写了电磁-热瞬态耦合仿真程序,对不同形状的电枢进行了动态响应分析[10-11]。谭赛采用棱边元法和节点元法,利用自由度平移法建立了电磁热物理场耦合有限元数值计算模型,并与由EMAP3D软件所计算的结果对比,验证了该模型的正确性,但研究中忽略了运动过程中枢轨之间的应力应变情况以及与磁场和温度场之间的耦合关系[12-14]。林庆华利用LS-DYNA软件,基于有限元和边界元结合的方法,实现电磁-热-结构场之间载荷传递的耦合模型计算,对发射过程中枢轨的电流密度、温度及应力的分布进行了详细的分析,但该模型只考虑了电磁场对温度场和结构场的单向耦合作用[15-16]。王烝考虑焦耳热、摩擦热和接触电阻热的瞬态特性,对增强型电磁轨道炮导轨的瞬态温升及瞬态扩张量分布进行了计算,但模型中忽略了导轨形变对电磁场和温度场的影响[17]。
在上述研究中,忽略了极端条件下电磁轨道发射装置复杂的电磁热力强耦合对导电、导磁及枢轨相关材料性能的变化,未对枢轨同时进行三维瞬态电磁热力强耦合计算分析。针对以上问题,笔者利用毕奥-沙伐定律推导了枢轨的磁感应强度计算公式,建立其三维瞬态电磁场数值模型并求解发射过程中枢轨的瞬态电磁力及磁感应强度。从摩擦系数、枢轨材料特性和接触压力瞬态特性的角度考虑枢轨瞬态温升和应力分布情况,分析了动态发射状态下枢轨的磁感应强度、电流密度、温度场和应力场的分布特征。
1 多物理场条件及控制方程
在电源、轨道以及电枢形成的闭合回路中,变化的电场会在两个轨道中间产生变化的磁场,磁场与流经电枢的电流相互作用形成强大的电磁力,推动电枢和弹丸沿着轨道方向做直线加速运动。在运动过程中速度、位移、应力等动力学响应同时也影响枢轨的电磁场分布。
多物理场强耦合关系如图1所示,当电枢运动时,产生的瞬态电磁力和焦耳热分别影响电枢和轨道的应力和温度变化分布;在发射极短过程中会存在极大温升,温升的主要来源是轨道体电阻产生的焦耳热及电枢高速滑动产生的摩擦热,同时温度的变化会引起材料电导率、弹性模量和热导率的变化,从而影响焦耳热及应力分布;枢轨接触面变化的接触力,主要是由电磁力和过盈力作用产生的正压力及热膨胀产生的热应力组成,考虑接触压力对界面电导的影响,从而直接影响电磁场中电流密度的分布情况。在建立模型时,将充分考虑在极端冲击条件下对材料特性的变化影响,以及在不同瞬间分析时考虑应力、温升及电磁场综合影响,为定量分析系统各种场量提供基础数据。

1.1 电磁场控制方程
对于电磁轨道发射装置计算模型,由于传导电流远大于位移电流,可以忽略位移电流的影响,认为是磁准静态场,瞬态电磁场的控制方程为
(1)

(2)
J=Js+σ(v×B),
(3)
式中:E为电场强度;B为磁感应强度;J为电流密度;H为磁场强度;Js为外部电流密度;v为电枢运动速度;σ为材料的电导率。
将轨道看成是由无数多根电流直导线组成的均匀载流长导体,载流直导线外任意点的磁感应强度为
(4)
式中:I为激励电流;u0为磁导率;θ1、θ2分别为点与导线两端的夹角;r为点到导线的空间距离。
根据式(4)可计算均匀载流导轨中任意点P(x,y,z)的磁感应强度为
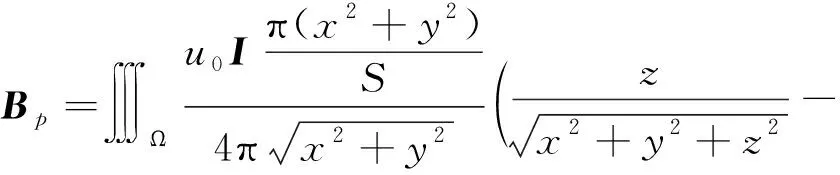
(5)
式中:S为轨道的横截面积;z0为电枢运动过程中z方向的位置。
对枢轨所在区域进行体积分,枢轨上任意电流元在电枢上某点a(x0,y0,z0)的磁感应强度为
(6)
(7)
电枢受到的电磁驱动力为
(8)
式中,V1为电枢体积。
1.2 温度场控制方程
发射过程中,激励电流为毫秒级脉冲且电枢高速运动,电流产生的焦耳热及电枢高速滑动过程中产生的摩擦热成为热载荷的重要来源。枢轨的热传导方程为
(9)
式中:ρm为材料的质量密度;T为温度;C为材料的比热容;k为热传导系数;μf为摩擦系数;fc为枢轨接触面处的压强。
在求解域中,所有边界处的边界条件均为绝热边界条件,即

(10)
式中,n为边界法向量。
1.3 力场控制方程
由于枢轨产生温升或温度分布不均时,结构体内部将会产生热应变,力学控制方程为
(11)
εT=a(T)ΔT,
(12)
式中:u为电枢运动位移;εT为热应变;s为应力;a为材料的热膨胀系数,随温度变化。
电枢高速运动会引起枢轨接触表面发热、变形和磨损等,从而影响摩擦系数,考虑滑动速度对摩擦因数的影响:
μf=(a+bv)e-cv+d,
(13)
式中:a、b、c、d由枢轨材料性质和压力载荷决定;v为电枢运动速度。
假设粗糙面各向同性,且表面粗糙度是在塑形形变的条件下,可以用Cooper-Mikic-Yovanovich (CMY)关系来计算接触面传导率。其计算模型为
(14)
式中:σ1、σ2分别为电枢和轨道的电导率;m和h分别为表面粗糙度的粗糙平均斜率和平均高度;Hc为较软材料的硬度;P为接触压力,界面电导分布与枢轨材料特性及接触压力分布有关。
2 计算模型及边界条件
应用COMSOL Multiphysics软件建立了电磁轨道发射装置电磁热力强耦合计算模型,如图2所示。轨道为长方体结构,长2.5 m,宽40 mm,高20 mm,所用材料为紫铜,其导电性能良好;电枢采用C形结构,所用材料为7075铝合金,其结构紧实,强度高,耐磨性强。

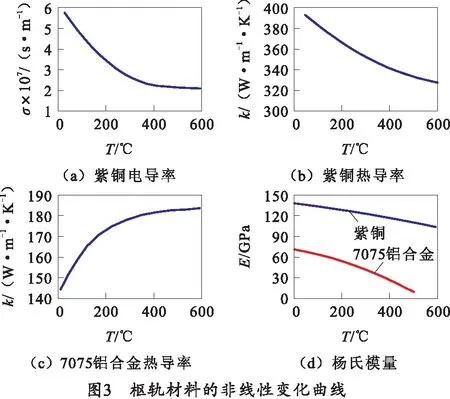
在模型中,考虑枢轨材料的非线性变化情况,通过查阅《铝合金应用手册》《铜加工技术实用手册》书籍得到材料性能参数和非线性变化曲线,如表1和图3所示。

表1 材料属性参数
在轨道通电后,枢轨周围都存在磁场,将枢轨看作一个系统,几何形成装配体,将枢轨的上下接触面分别设为接触对,瞬态电磁力作为力学场的体载荷。对轨道两侧施加固定约束,发射初始阶段对轨道两侧面施加一定的预压力能够保证枢轨良好接触,初始接触力可以通过设置合适的过盈量来实现。在极端工作条件下,由于作用力发生在极短的时间内,温升急剧升高,相对散热极小,将轨道与空气域视作绝热处理,在初始时刻,将枢轨温度设为25 ℃,考虑轨道电阻焦耳热及枢轨滑动产生的摩擦热;金属轨道内部的温度分布不均匀,各质点之间相互制约,以及结构上存在外在约束,使其不能完全自由胀缩而产生热应力,电枢受到热膨胀作用对两侧轨道产生压力,结构体将产生热应变,通过“热膨胀”物理场接口实现耦合计算。
通入枢轨的激励电流如图4所示。电流的上升沿约为0.75 ms,峰值为0.6 MA,激励时间为2.8 ms。

3 计算结果及分析
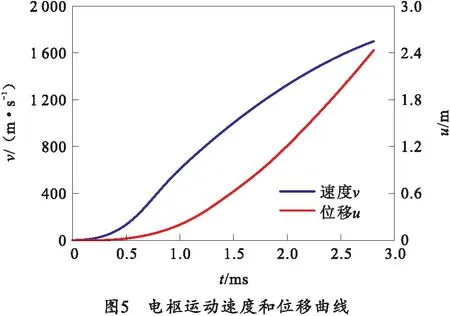
根据模型计算得到电枢运动速度和位移曲线,如图5所示。电枢在2.8 ms时从轨道出口滑出,出口速度约为1 700 m/s。
3.1 电磁场计算结果
根据Comsol电磁场计算结果可以得到轨道之间的磁感应强度分布,电流峰值时刻电枢前后轨道间磁感应强度分布如图6所示。

由图6可见,电枢前端在轨道中间产生的磁感应强度约为6 T,后端可达到9 T,磁感应强度增大明显,电枢磁感应强度在轨道两侧方向呈现马鞍面分布,由中心向两侧方向逐渐增加。电流趋肤效应导致电流集中在轨道表面处,使得枢轨接触面区域磁感应强度增大明显,达到8 T。
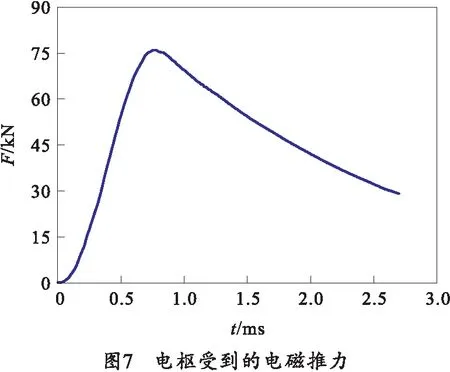
对电磁轨道发射装置的瞬态电磁力进行数值计算,如图7所示。在峰值电流为0.75 ms时,电枢在运动中受到的电磁推力最大,可达到76 kN。
电流密度在电枢和枢轨接触面的分布情况如图8和9所示。
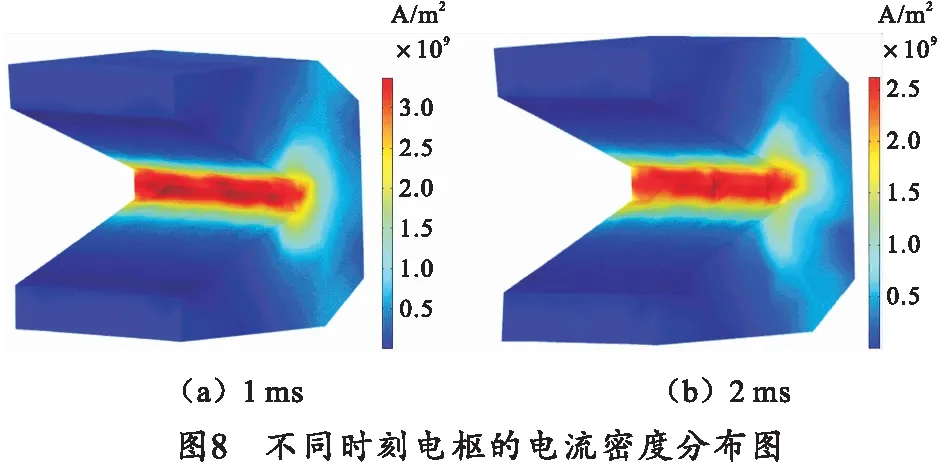
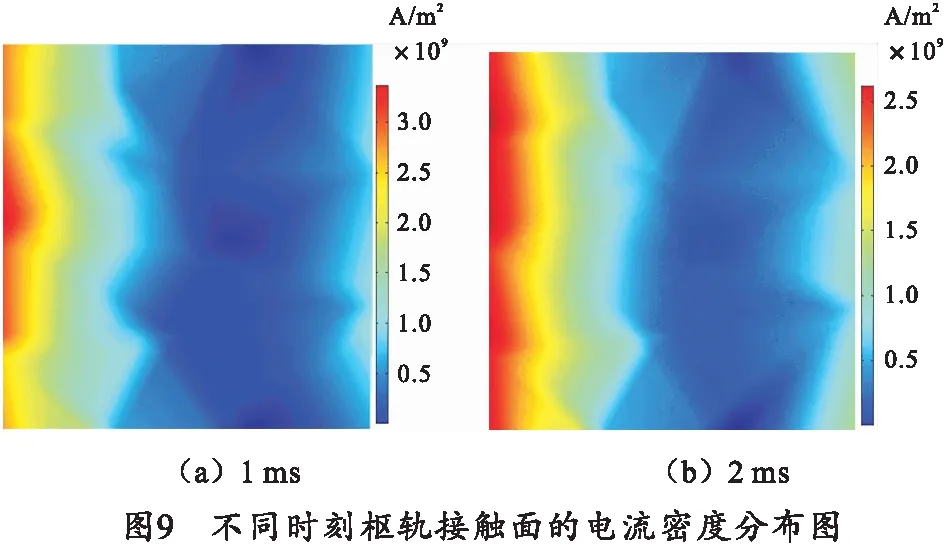
如图8、9可知,在发射过程中,电流密度集中分布在电枢喉部及枢轨接触区域,最大可达到3 GA/m2。电流密度呈U形分布并出现逐渐向两侧分布的趋势。受电枢高速运动的影响,电流集中在导体边缘并逐步向枢轨接触面的尾端方向扩散。
3.2 温度场计算结果
通过强耦合计算模型可得到发射过程中电枢和轨道的最高温度曲线,如图10所示。

由图10可知,电枢向前加速运动,在出口处其最高温度可达到690 ℃,根据曲线斜率可计算出最高温升速率可达到4×105℃/s。轨道最高温度可达到110 ℃。在发射过程中,电流在0.75 ms之前处于上升期,电流较小,电枢刚开始运动,温升较缓慢;在0.75 ms之后,电流升高至峰值,温升速度开始加快,几乎呈现线性增长。图11和12分别为电枢和轨道的温度分布。
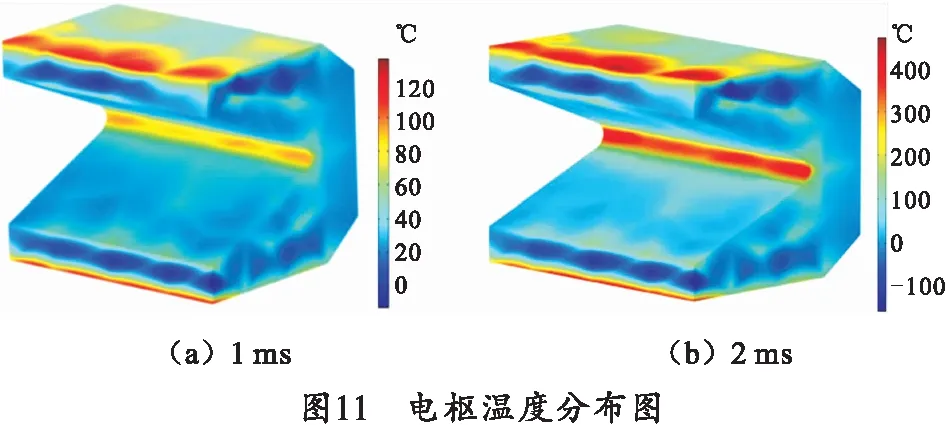
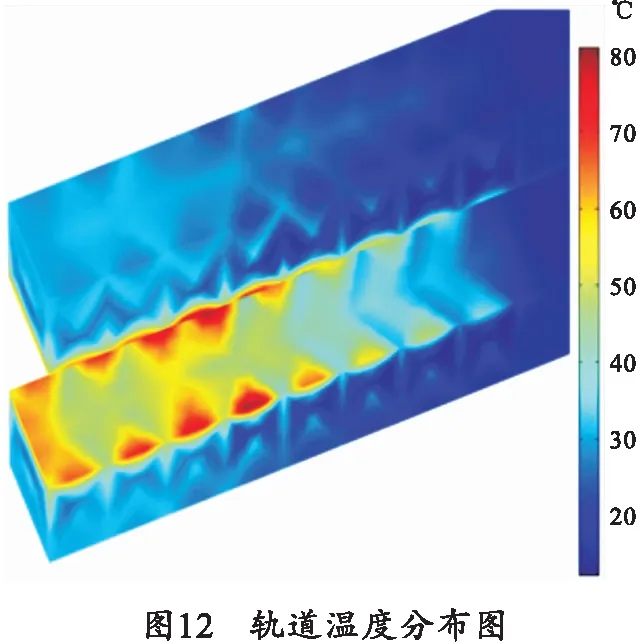
由图11、12可知,由于电流密度集中分布在电枢喉部和枢轨接触面,因此枢轨最高温度也主要分布在电枢喉部及接触面区域。轨道的高温区域不断向着出口方向延伸,轨道温升最高区域在轨道两侧,特别是靠近轨道棱角处,最高温度达到80 ℃。该位置由于电流密度分布大,截面积很小,因此导致高温区域沿轨道棱线集中分布,轨道其他区域的温升变化不明显,在电流密度分布较小区域的温度与室温相似。
轨道体电阻产生的焦耳热和枢轨滑动摩擦产生的摩擦热如图13、14所示。
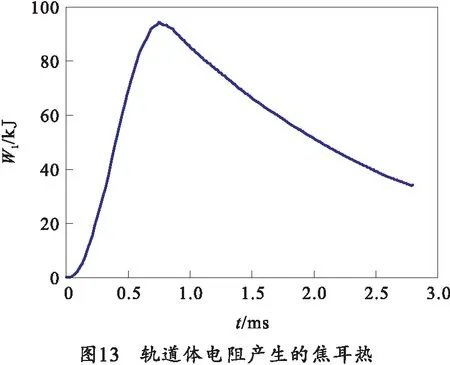
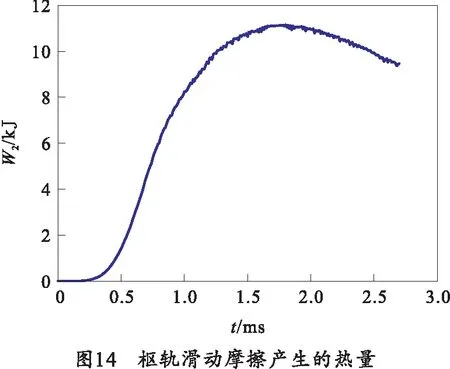
由图13、14可知,发射过程中产生的热量随着电枢高速运动发生瞬态变化,焦耳热在电流峰值时刻达到最大值约为100 kJ,之后随着电枢运动,表现出逐渐递减的趋势。与电枢运动速度和位移曲线相对应,枢轨滑动摩擦热在电枢位移为0.5~1.5 m时达到最大值,约为11 kJ。热量来源在电枢运动初始阶段以轨道体电阻焦耳热为主,之后滑动摩擦热量逐步上升。与文献[18]相比,摩擦热量曲线分布规律性一致,均呈现先增后减的变化趋势。在计算摩擦热时,考虑了摩擦系数随速度变化的瞬态特性,根据计算模型发射过程中电枢运动速度及温度变化的相关曲线图,与式(13)的大致趋势相对应,可以作出摩擦系数随速度变化的曲线,如图15所示。
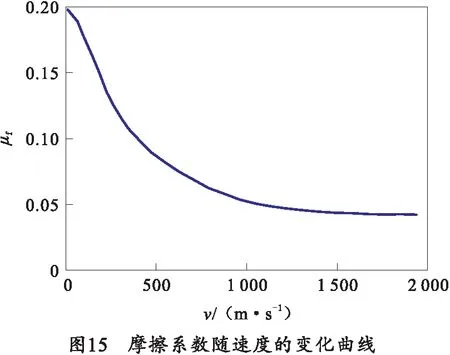
在发射过程中,由于焦耳热的作用,电枢启动时即进入由干滑动摩擦向流体润滑的过渡边界润滑阶段,此时摩擦系数上限值为初始干滑动摩擦系数。随着发射进程中速度不断增大,温度不断升高,摩擦系数逐渐降低,在电枢温度达到600 ℃、速度达到1 500 m/s时摩擦系数稳定在0.04左右。
3.3 力场计算结果
在发射过程中,不同时刻电枢的应力分布如图16所示。

由图16可知,电枢的应力分布特征与其温度分布相似,最大应力主要出现在电枢喉部及枢轨接触面处。在初始时刻,轨道两侧的预压力作用在电枢上,因喉部区域面积小,集中在喉部区域。随着电枢高速运动,电枢温度迅速升高,金属轨道内部的温度分布不均匀,且存在固定约束,使其不能完全自由胀缩而产生热应力,电枢应力值主要由电磁力、热应力及预压力共同组成。因摩擦热量主要体现在枢轨接触面上,因此接触面的热应力值升高明显。电枢喉部处的应力值最大可达到375 MPa,考虑结构场和温度场的耦合作用,所选用的7075铝合金材料的屈服强度随着温度升高会下降,在出口时刻,电枢温度达到最高,使其结构刚度受到影响,可能会导致电枢的变形。
电枢和轨道之间的接触压力主要包括由电磁力、过盈力作用产生的正压力及热膨胀产生的热应力,通过电磁场与结构场的耦合作用,得到了枢轨的接触压力变化曲线,如图17所示。
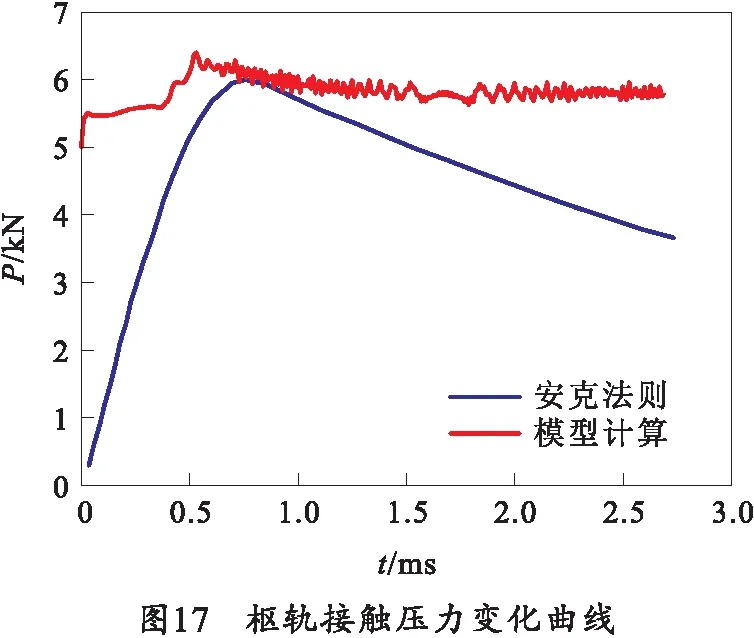
由图17可知,结构本身的刚度作用使得枢轨之间的接触压力呈现振荡变化,一般基于Marshall的安克法则(1g/A)来判断电枢与轨道的接触压力[19],如果接触压力小于10 N/kA,则枢轨接触状态较差,容易发生转捩。通过模型计算对比,在电流峰值时刻枢轨的接触压力接近于安克法则的接触压力,其余时刻均大于计算的接触压力。
4 结论
针对电磁轨道发射装置的电磁热力多物理场强耦合计算问题,主要得到了以下结论:
1)利用毕奥-沙伐定律推导了枢轨的磁感应强度计算公式,建立其三维瞬态电磁场数值模型,得出在电流峰值时刻,电磁推力达到最大值;枢轨的电流密度、磁感应强度集中分布在电枢喉部及枢轨接触面区域。
2)从摩擦系数瞬态变化的角度分析轨道电阻焦耳热和滑动摩擦热共同对枢轨瞬态温升的影响,得出温升变化明显的区域体现在电枢喉部、轨道外侧棱线及枢轨接触面,热量来源在初始阶段以轨道电阻焦耳热为主,之后摩擦热量逐步上升,摩擦系数随着速度的增加而减小,最终趋于稳定值。
3)从枢轨材料非线性变化以及接触压力瞬态特性的角度分析枢轨的应力分布情况,得出热应力集中分布在电枢喉部及枢轨接触的边缘区域,接触压力呈现出振荡变化。
强耦合计算能够获取发射过程中实时物理量参数,为材料进一步设计制造和系统可靠性预测奠定基础。

