基于高精度子通道程序的棒束临界热流密度机理模型

郭俊良,蒋 理,高 逵,孔焕俊,桂 淼,单建强

(西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049)

为了提高压水堆核电站的经济性,过冷沸腾因其高热流密度和高换热系数成为首选的沸腾模式[1]。由于堆芯内工质的低含汽率和泡状流流型,容易发生偏离核态沸腾(DNB)。当发生DNB型沸腾危机时,燃料包壳表面被大量汽膜覆盖导致传热能力的恶化,严重威胁着反应堆的安全。因此,准确预测棒束临界热流密度(CHF)并提高CHF是压水堆设计的最终目标,以提高反应堆的经济性和安全性[2]。

由于压水堆堆芯燃料组件复杂且独特的几何形状(如紧凑的棒束结构、搅混翼格架和导向管)以及宽范围的运行工况,准确预测棒束CHF具有一定的挑战性。目前,工程上常用的棒束CHF预测方法是针对感兴趣的工况开展大规模棒束CHF实验并利用其数据开发特定棒束结构的CHF关联式。使用子通道分析程序建立特定棒束几何结构的数学物理模型,并采用集总参数的方法将子通道内的“平均”参数作为“局部”参数输入到CHF关联式中拟合出最优系数。工程上常用的关联式如EPRI[3]、WRB-2[4]以及FC-2000[5]均采用上述方法得到。然而,现有的子通道分析程序对子通道的划分较为粗糙,不能准确刻画燃料棒表面附近局部流场的细节,特别是搅混翼格架和导向管存在的情况下。而DNB型CHF又是一个局部现象,因此,需要在CHF关联式中反映搅混翼格架和导向管(冷壁效应)的影响[5]。CHF关联式的应用受限于棒表面局部参数计算的准确性,这也是为什么特定的CHF关系式只能用于特定棒束的原因。准确计算棒表面的局部参数是准确预测CHF的前提。

除了准确计算棒表面局部参数外,棒束CHF预测面临的另一大挑战是CHF的预测方法,包括机理模型、关联式以及查询表[6]。CHF机理模型以物理机制为基础,可以适当的外推并提供正确的参数趋势,一直是众多学者研究的对象。此外,CHF机理模型可以为新型燃料组件或新型堆提供适当的预测。在过去的几十年中,针对不同热工水力条件已经建立了许多CHF机理模型[7-9]。其中Weisman等[7]的模型适用于最广泛的工况范围,并且已被应用于棒束CHF的预测。然而,Weisman等的模型在应用于棒束CHF预测时受限于子通道局部参数的不准确性,预测精度不高,且对于导向管栅元CHF预测时仍需进行冷壁效应的额外修正[10]。因此,本研究基于高精度子通道分析程序建立一个棒束CHF机理模型,并试图摆脱搅混翼格架和导向管对CHF模型的修正,使CHF的预测重新回到局部现象的本质。

1 高精度子通道分析程序

ATHAS(Advanced Thermal-Hydraulics Analysis Subchannel)是西安交通大学开发的具有自主知识产权的热工水力子通道分析程序。该子通道分析程序基于漂移流模型,采用全隐式压力-速度修正算法求解,具有较高的预测模拟精度。最近Dong等[11]基于分布式阻力模型开发了一种用于ATHAS的搅混翼横流混合模型;Jiang等[12]同样基于分布式阻力模型建立了高精度子通道分析程序。本文简要介绍高精度子通道分析程序的子通道划分和相关本构,具体细节参考文献[12]。

1.1 精细化子通道划分

在子通道分析中,人为地将棒束通道划分成若干个子通道并假设每个子通道内的热工水力行为像圆管一样,且子通道大小的划分是任意的。如果子通道划分得太细,则必须考虑两相微观结构的细节;如果子通道划分得过于粗糙,则无法准确预测感兴趣的棒表面的局部流动参数[13],精细化子通道划分就是在这种情况下提出的。在传统子通道划分的基础上,根据搅混翼格架叶片分布的特点,将子通道进一步细分。传统子通道和精细化子通道的划分方法分别如图1所示。

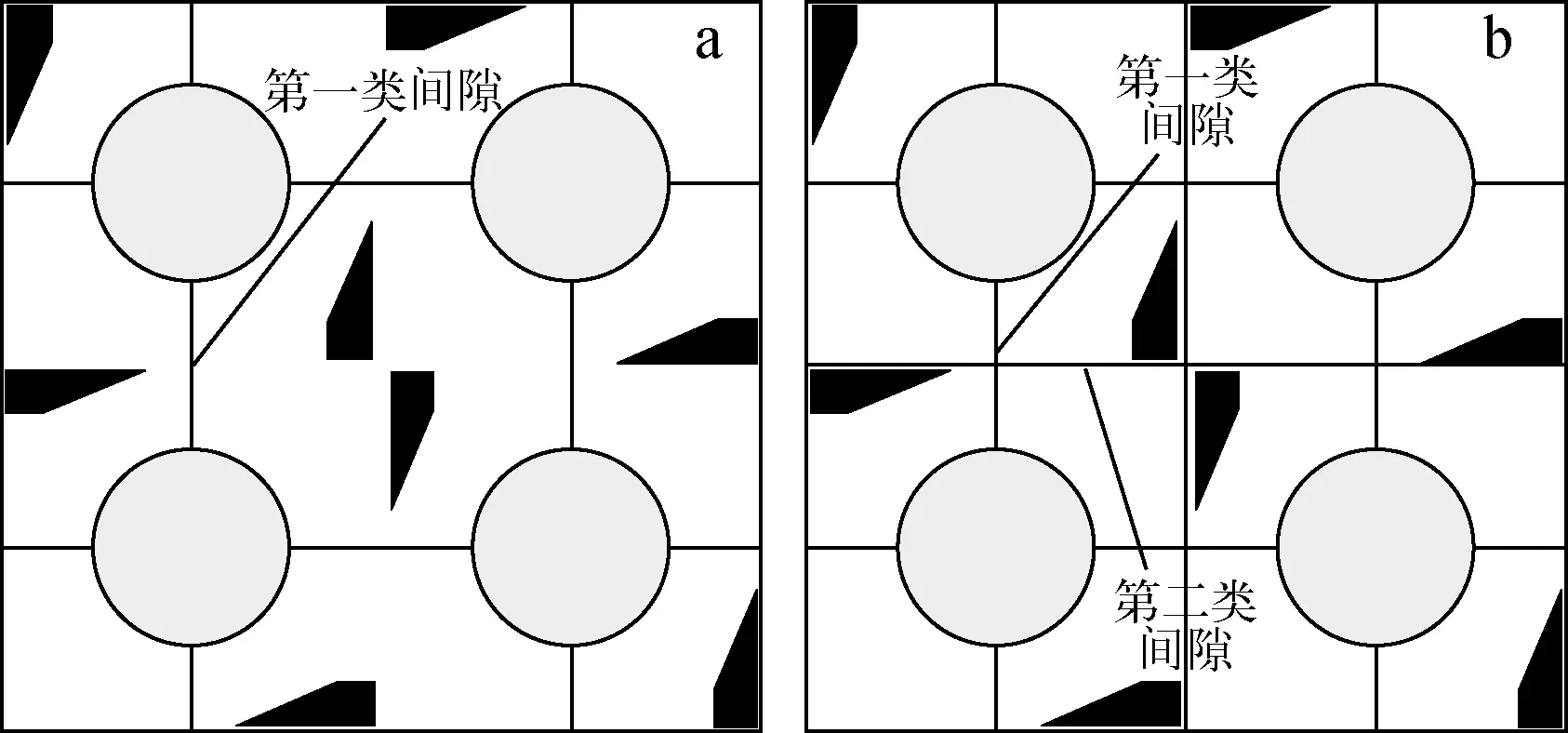
a——传统子通道划分;b——精细化子通道划分

精细化子通道划分后,每个子通道内至多存在1个搅混翼叶片,因此能够更好地适用于格架分布式阻力模型。另外,相比于传统子通道,更细致的划分可以相对更准确的计算出棒表面的局部参数且能得到传统子通道内部的横流。虽然更细致的子通道划分使子通道和间隙数量都大大增加,但计算效率仍远高于CFD类软件。

1.2 搅混翼格架分布式阻力模型

分布式阻力模型最早应用于钠冷快堆绕丝形阻的分析,通过受力分析将绕丝对流体的作用力加入到动量方程中[14]。类似的,也可将燃料棒和搅混翼格架对流体的作用力用表达式量化以反映其对流体的作用,这就是搅混翼格架分布式阻力模型的基本思想。流体在经过搅混翼格架所在的轴向控制体内分别受到来自燃料棒以及搅混翼叶片的作用力。将燃料棒的阻力沿轴向和径向分解为轴向力Fu和横向力Fv,搅混翼叶片的作用力沿叶片切向和法向分解为Fu1和Fv1。流体的受力示意图如图2所示。用同样的方式将流体的总速度vall以两种方式分解(轴向和横向分解,切向和法向分解),如图3所示。

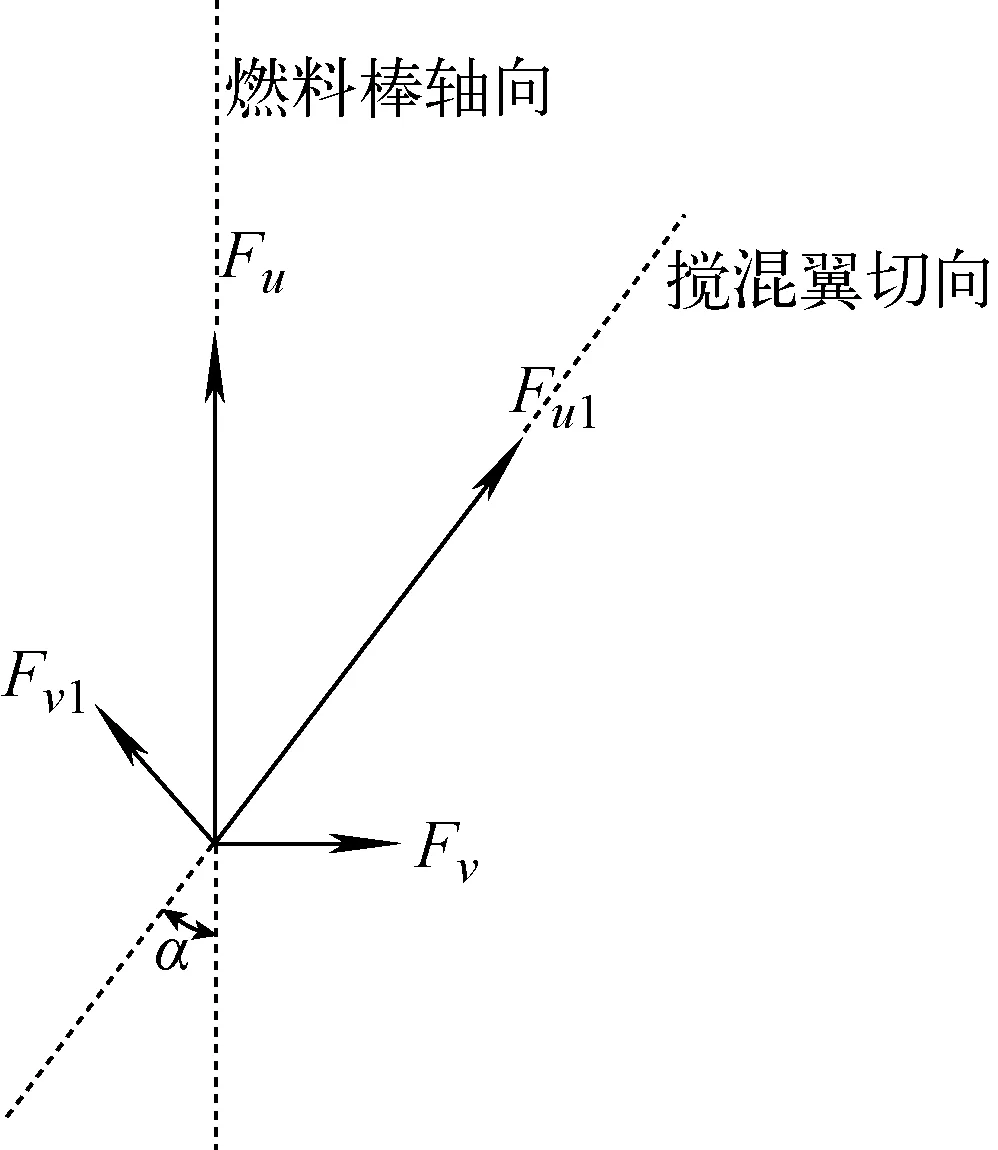
图2 流体受力示意图

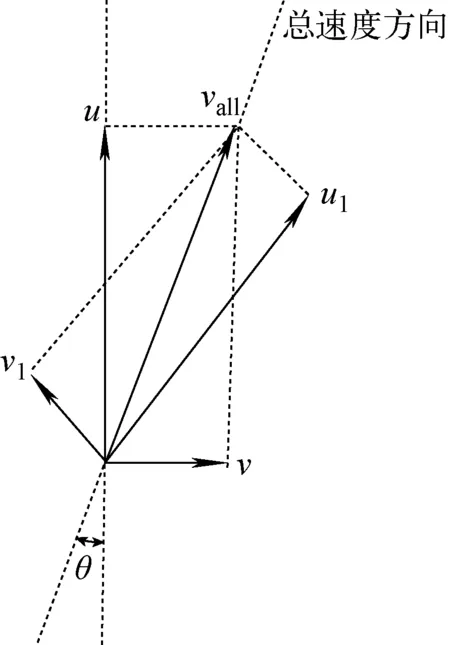
图3 速度分量示意图

利用Rehme轴向阻力关系式[15]和Gunter-Shaw横向阻力关系式[14]计算速度对应方向的阻力并加入到轴向和横向动量方程中,对应的关系式如下:

(1)

(2)

(3)

(4)

式中:AR、AM分别为燃料棒和搅混翼叶片的润湿面积;fR、fM分别为燃料棒的轴向摩擦系数和搅混翼的切向摩擦系数;CR、CM分别为燃料棒的横向摩擦系数和搅混翼的法向阻力系数;ρ为流体密度;u、v分别为轴向分速度和横向分速度;u1、v1分别为切向分速度和法向分速度。

此外,传统子通道分析方法大多假设子通道中轴向的流动占主要地位,忽略横流对流项。相关研究表明[16],搅混翼所引起的定向横流可以达到与轴流相同的数量级,忽略横流对流项显然是不合理的。因此,高精度子通道分析程序在动量方程中加入了横流对流项,同时考虑搅混翼所在的子通道与其下游子通道之间的不完全耦合。横流对流项表达式为:

GSK=〈N〉CSK·ρAKvK

(5)

式中:GSK为横流对流项;〈N〉表示横流方向;CSK为不完全耦合系数;AK为间隙处的横向面积;vK为间隙处的流速。

1.3 湍流搅混模型

相邻子通道之间除了横向压差引起的横流以及搅混翼引起的定向横流外,湍流搅混也是子通道间质量、动量以及能量交换的一种重要作用机制。子通道之间的湍流搅混本质上是以涡的形式进行传递的。但由于壁面阻碍导致径向涡的扩散受到制约,其扩散系数小于周向涡扩散系数,涡扩散系数呈各向异性[17]。对于传统子通道划分所形成的第一类间隙而言(图1a),湍流搅混方向平行于棒表面(周向搅混)。而对于精细化子通道划分所新形成的第二类间隙(图1b),湍流搅混方向垂直于棒表面(径向搅混)。因此,这两类间隙的湍流搅混速率是不同的。ATHAS中的湍流搅混模型分别计算两类不同间隙的湍流搅混速率。

第一类间隙的湍流搅混速率采用Carlucci等[18]的模型来计算。总的湍流搅混速率由汽相搅混和液相搅混两部分组成,而每一部分又分为均相部分和汽泡引起的附加部分:

w′l=w′l,hom+w′l,inc

(6)

w′g=w′g,hom+w′g,inc

(7)

式中:w′l、w′g分别为液相、汽相搅混速率;w′l,hom、w′g,hom分别为液相、汽相均匀部分搅混速率;w′l,inc、w′g,inc分别为液相、汽相附加部分搅混速率。

对于第二类间隙,考虑到1个棒与其周围4个子通道中第二类间隙的搅混类似于环管的径向搅混[19],因此第二类间隙处的湍流搅混速率采用基于Levy[20]提出的环管涡扩散系数表达式以及普朗特混合长度理论推导得到:

(8)

式中:w′为单相搅混速率;l为棒表面到间隙的距离;τ为剪应力;Sij和zij分别为间隙宽度和相邻子通道的质心距。

两相湍流搅混倍增因子采用Beus[21]模型计算,在得到总的两相湍流搅混速率后用含汽率进行加权从而分别得到汽相和液相的湍流搅混速率。

高精度子通道分析程序ATHAS已经过GE 3×3棒束实验[22]及PSBT基准题[23]的验证,计算值与实验值符合很好,与传统子通道计算结果相比精度大幅度提高。

2 棒束CHF机理模型开发

2.1 圆管汽泡壅塞模型

Weisman等[7]将整个流动区域划分成汽泡层区和主流区,如图4所示。汽泡层区与主流区之间的湍流交换被认为是CHF触发的核心机制。当汽泡层内的空泡份额超过临界空泡份额(α2=0.82)时,大量汽泡壅塞在一起从而阻碍了涡向壁面的径向输运,导致CHF的发生。

图4 汽泡层与主流区输运示意图

对汽泡层区和主流区分别建立质量守恒方程,联立可得:

G′(x2-x1)=qb/hfg

(9)

式中:G′为两个区域交界面处的径向脉动质量流速;x1为主流区的真实含汽率;x2为汽泡层区的真实含汽率,由α2=0.82计算得到;qb为用来产生蒸汽的热流密度;hfg为汽化潜热。

qb采用Lahey等[13]的模型计算:

(10)

式中:q为总热流密度;hl和hf分别为主流区过冷液体焓和饱和液焓;hld为汽泡脱离点的焓,由Levy[24]模型计算得到。

将式(10)代入式(9)并整理成无量纲的形式,即可得到Weisman模型的CHF(qCHF)表达式:

(11)

交界面处的G′由湍流强度与轴向质量流速计算得到,并考虑壁面产生的蒸汽会阻碍主流到汽泡层的径向脉动。通过引入参数Ψ得到有效湍流脉动到壁面的比例。在交界面处,G′的计算表达式为:

G′=GibΨ

(12)

式中:G为轴向质量流速;ib为径向湍流脉动强度;Ψ为一个关于壁面蒸汽速度的复杂函数。

径向湍流脉动强度由圆管单相径向脉动速度分布拟合得到[7],同时考虑两相脉动倍增因子。径向湍流脉动强度ib为:

[1+a(ρl-ρg)/ρg]

(13)

式中:k为经验系数,文献[7]中为2.4;Db为汽泡直径;D为圆管直径;a为与质量流速相关的经验系数;ρl和ρg分别为液相和汽相的密度。

2.2 相关本构的修改

1) 棒束近壁区的湍流强度

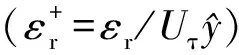
图5 等效圆管示意图

由于棒表面到零剪应力位置的距离不是定值,而子通道分析是采用集总参数的方法,须对零剪应力位置距离进行平均。通过敏感性分析计算,用不同的权(包括使用最大距离和最小距离的算数平均)对距离进行加权,结果变化最大为2%。因此,仿照子通道的水力直径的定义,以(rm(θ)+ri(θ))为权重进行加权,推导等效圆管直径如下:

(14)

从式(14)可看出,等效圆管的平均直径与子通道的水力直径定义类似,只不过分母为湿周与第二类间隙长度的总和。以此平均直径替换式(13)中的圆管直径D可将圆管表面的湍流强度分布转换成棒表面的湍流强度分布,相比于之前的方法更具有物理意义。

需要强调的是,子通道的水力直径和等效圆管直径分别独立,在计算子通道的局部参数时使用的仍是子通道的水力直径,在CHF模型中计算湍流强度分布时使用的是等效圆管直径,该直径只是为了将圆管湍流强度分布转成棒束湍流强度分布。CHF是一个局部现象,子通道分析程序在CHF预测中的作用是尽可能来提供相对更准确的、集总的局部参数,棒表面的湍流强度分布不应受子通道的划分而随之改变,因此独立开来。

2) CHF位置处的汽泡直径

在Weisman的CHF机理模型中,采用Levy[24]模型来计算汽泡脱离直径,并将此直径作为CHF发生位置处的汽泡直径。Levy模型是基于单个附着在壁面上的汽泡的受力平衡模型,其计算表达式如下:

(15)

使用该模型计算汽泡脱离点的直径是合理的,但在CHF发生位置处由于大量汽泡壅塞在一起,汽泡被压扁成长径比为3/1的椭圆形汽泡(依据Wesiman的假设)。因此,式(13)中的汽泡直径不能用汽泡脱离直径代替。考虑到CHF发生位置处有大量汽泡滞留在壁面,壁面上的汽泡层厚度可被认为是粗糙度ε[27]。

按照Lee等[28]的假设,汽泡层边缘被认为当涡的大小为汽泡直径Db的k倍时,汽泡层便终止,因此汽泡层厚度yc可由式(16)计算得到:

(16)

式中,F2为两相混合普朗特长度倍增因子,F2=1。

将式(16)中的汽泡层厚度yc作为壁面粗糙度ε代入到式(15)进行迭代求解,即可得到CHF发生位置处的汽泡直径。

3 棒束CHF机理模型评价

将棒束CHF机理模型以子程序的方式嵌入到ATHAS中。CHF子程序中所涉及到的局部参数通过ATHAS的流场计算得到,CHF子程序在ATHAS计算流场收敛后被调用。输入参数为子通道程序计算局部参数值和流体物性值,输出是预测的CHF。

3.1 棒束实验数据

用来验证本机理模型的实验数据来自西安交通大学棒束CHF实验数据库。由于本模型是针对DNB型CHF开发的,选取其中空泡份额小于0.8的5×5棒束CHF数据进行评价。验证数据共有12组,总共601个棒束CHF数据点。实验数据工况范围列于表1,实验工况范围覆盖了压水堆的典型工况范围。表2列出实验布置情况及数据统计。表2中:N/A表示没有导向管;D为最后一个搅混翼格架距加热长度末端距离;gsp为搅混翼格架跨距;C/P为径向功率因子(中间棒和外圈棒的功率比值)。

表1 实验数据工况

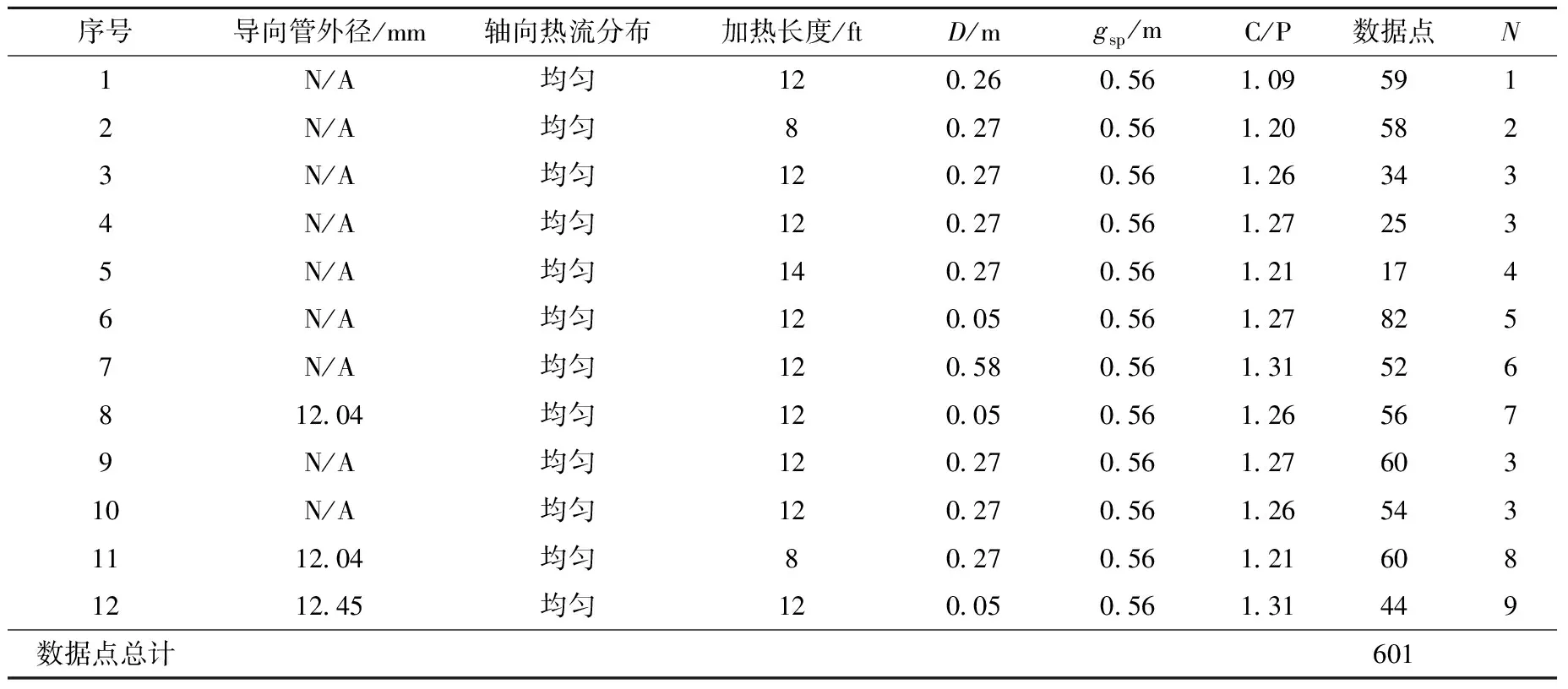
表2 实验布置情况及数据统计

3.2 棒束CHF机理模型评价

图6示出601个数据的预测CHF与实验CHF的比较。从图6可看出,几乎所有数据都在±15%的相对误差范围带内。预测值与实验值之比(P/M)的平均值Rav为0.99,均方差RMS为4.69%。由于高精度子通道程序将传统子通道一分为四并且增加了格架分布式阻力模型,因此可更准确地计算出传统子通道内局部参数的不均匀性,所计算出来的局部参数更能表征棒表面附近的流场。此外,结合本研究所开发的机理模型,均方差RMS可达到5%以内,优于目前任何一个棒束CHF机理模型。

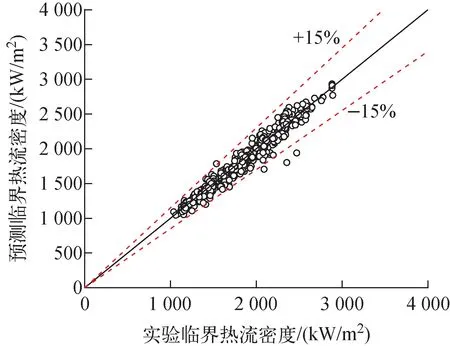
图6 预测CHF与实验CHF的比较

图7示出P/M随压力p、质量流速G、临界含汽率x的分布以检验其无偏性。从图7可见,P/M随质量流速和临界含汽率没有明显的参数倾向性,但似乎本模型在低压下(6～8 MPa)预测偏保守。这是由于本模型是基于Weisman模型进一步开发得到的,而在这个压力范围内Weisman模型预测圆管CHF本身就偏保守[29]。

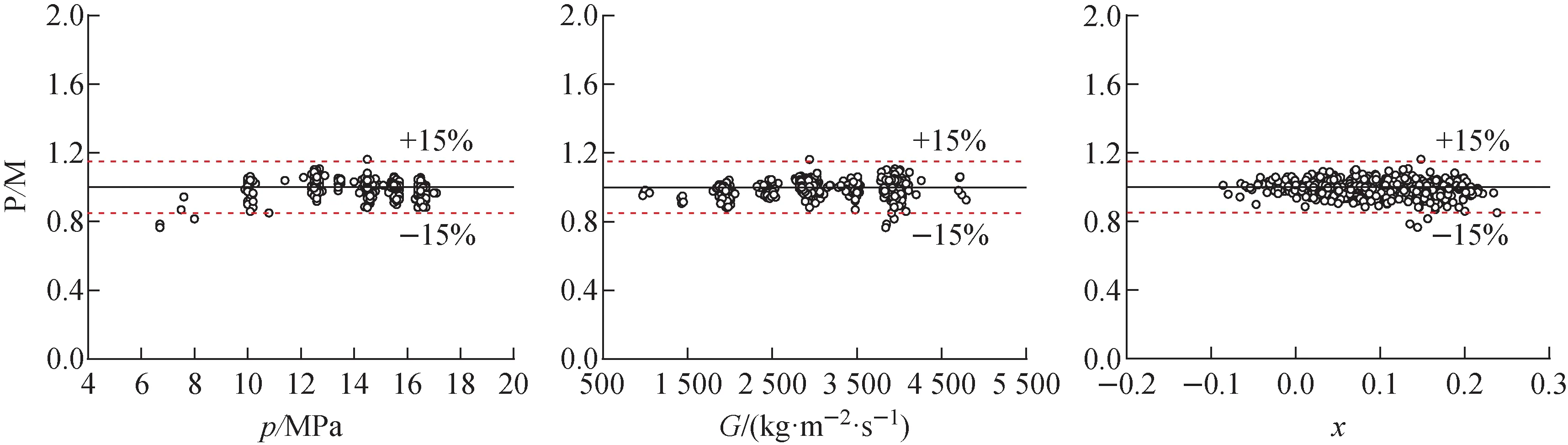
图7 P/M随压力、质量流速和临界含汽率的分布

表3列出不带导向管(典型栅元)和带导向管(导向管栅元)的分组误差统计,可以看出,本模型可很好地适用于带导向管和不带导向管的棒束CHF预测。冷壁效应的本质为在一个子通道内焓(或含汽率)存在分布,在用传统子通道计算棒束CHF时需进行冷壁效应修正。在将子通道细分后,则无需在CHF模型上进行任何修正即可成功预测带导向管的棒束CHF。本模型从机理层面上揭示了冷壁效应的本质。

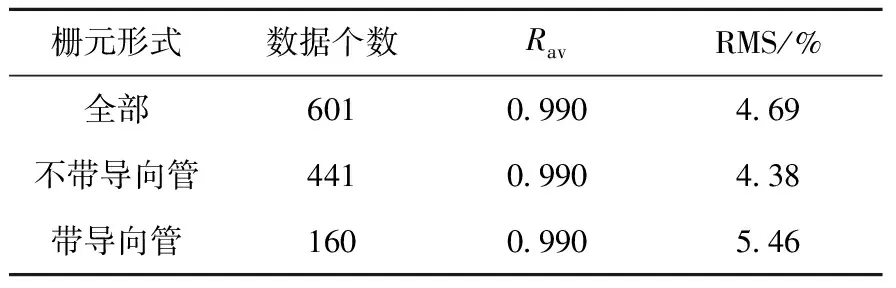
表3 冷壁无偏性检验

4 结论

本文基于高精度子通道程序ATHAS开发了棒束CHF机理模型,并采用5×5棒束CHF实验数据对模型进行了验证,主要结论如下。

1) 传统子通道划分方式过于粗糙,得到的集总参数不能表征棒表面的局部参数。基于CHF是一个局部现象的假设,使用高精度子通道程序ATHAS进一步细分子通道以获得相对更准确的棒表面局部参数。

2) 基于Weisman汽泡壅塞模型建立了棒束CHF机理模型,提出等效圆管的概念将圆管表面湍流脉动强度的分布转换成棒束表面的强度分布。考虑CHF发生位置处的汽泡壅塞造成的汽泡形变,将汽泡层厚度作为粗糙度迭代求解汽泡直径,使其更具有物理意义。

3) 使用5×5棒束CHF实验数据对本文模型进行了评价和验证,Rav为0.99,RMS为4.69%,预测精度优于目前现有的任何一个棒束模型。本模型结合高精度子通道程序,预测导向管栅元和典型栅元的棒束CHF时无需进行修正,是一个具有发展前景的棒束CHF机理模型。