基于动态轧制力的四辊轧机垂直震动及扭转震动特性探析

肖志明

（福建省三钢冶金建设公司，福建 三明 365000）

随着我国工业化进程的逐渐提升，轧机已经是各工厂中所必不可少的生产设备，但是在日常生产过程中，轧机振动问题一直为工作人员所困扰，一定程度上影响了企业产品质量的提升。而在如今轧机垂扭耦合系统非线性振动机理的研究还不是很完善，难以得到有效利用。所以，为了改变这一现状，对四辊轧机垂直震动及扭转震动特性的研究是十分必要的。本文在考虑动态轧制力的基础上，建立四辊轧机垂直—扭转耦合振动动力学模型，结合实际轧机工作参数对其性质进行研究。

1 动态轧制力和动态轧制力矩模型

在忽略润滑因素的影响下，依照轧制生产中轧制带材的受力情况，将轧制变形过程简化为如图1 所示的力矩模型。

图1 中各项标注分别为：稳态轧制时，轧件入口厚度H；稳态轧制时，轧件出口厚度h；轧辊半径R；轧件所受前张力τf；轧件所受后张力τb；上辊垂直方向振动位移x1；下辊垂直方向振动位移x2；辊旋转速度v0；轧件咬入角度α。

计算公式：

其中，K 为主应力影响系数， 通常情况下K=1.15σ，σ 是材料变形阻力；KT是张力影响系数；Qp是外摩擦影响系数；Le是轧辊和轧件接触弧的水平长度；B 是轧件宽度。

通过以下模型完成对材料变形阻力的计算。

将各式全部带入F=BleQpKTK 后进行泰勒展开，可得动态轧制力为：

其中，ΔF 代表轧制力动态变化量；F1代表稳态轧制力。

2 四辊轧机垂直-扭转耦合振动动力学模型

考虑到动态轧制力和动态轧制力矩的影响，建立四辊轧机垂直—扭转耦合振动动力学模型见下图2 所示。

图2 四辊轧机垂直-扭转耦合振动动力学模型

图2 中各项标注分别为：

上辊旋转角度θ10；下辊旋转角度θ20；上下传动系统电机端旋转角分别为θ30、θ40；上下辊系上动态轧制力矩为T1、T2；上下辊系所受等效合力为P1、P2；上辊系与上横梁间的等效阻尼c1；下辊系与下横梁间的等效阻尼c2；上下辊系与电机端间的等效阻尼为c3、c4；上辊系与上横梁间的等效刚度k1；下辊系与下横梁间的等效刚度k2；上下辊系与电机端间的等效刚度为k3、k4；上下辊系等效转动惯量为J1、J2；上下辊系的等效质量为m1、m2。

由此可以得到四辊轧机垂直—扭转耦合振动方程为：

在工作辊质量远小于支撑辊时，因为轧机结构与振动的对称性，存在m1=m2，k1=k2，c1=c2，y1=y2，x1=x2，p1=p2，J1=J2，k3=k4，c3=c4，θ1=θ2，θ3=θ4，T1=T2。

令y=x1可得：

3 四辊轧机耦合振动方程主共振响应求解

设轧机在轧制过程中，受到周期性的外部扰动

设其解为：

代入后令，消除久期项得：

4 仿真分析

图3 和图4 为变化参数条件下的幅频曲线。

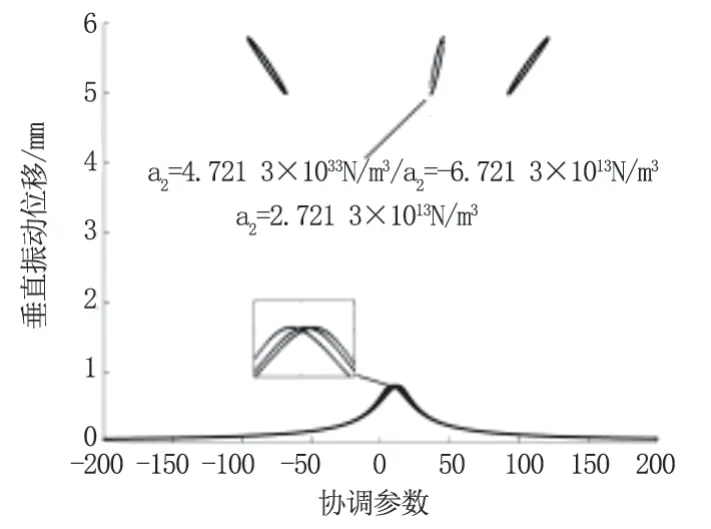
图3 a2 变化下竖直方向共振幅频

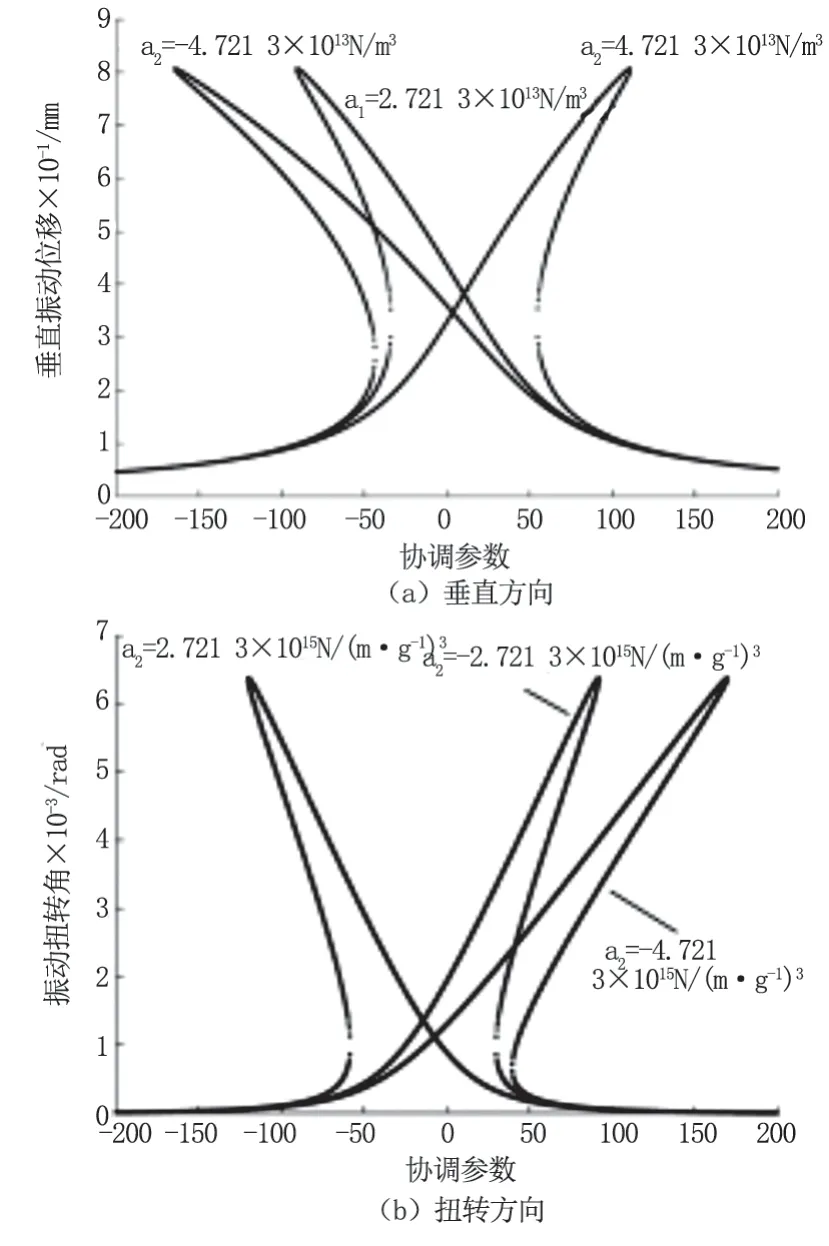
图4 a2 变化时垂直和扭转方向主共振幅频曲线

图3 是指在系数a2 发生变动的情况下，轧机幅度频率曲线有“跳跃圈”现象发生，在这时在跳跃圈范围里轧机会发生非常明显的主共振现象。

图4 为参数a2 在较大值变化下，轧机垂直和扭转方向幅频特性曲线。从图中我们能够得到的信息是a2的变动不仅能够使轧辊在垂直方向发生跳跃，也能够使轧辊在扭转方向发生跳跃现象。

图5 中为外扰力幅值F0 变化下轧机在垂直和扭转方向的全局分岔曲线。可以看出，轧机在垂直和扭转方向都出现了多种运动形态。

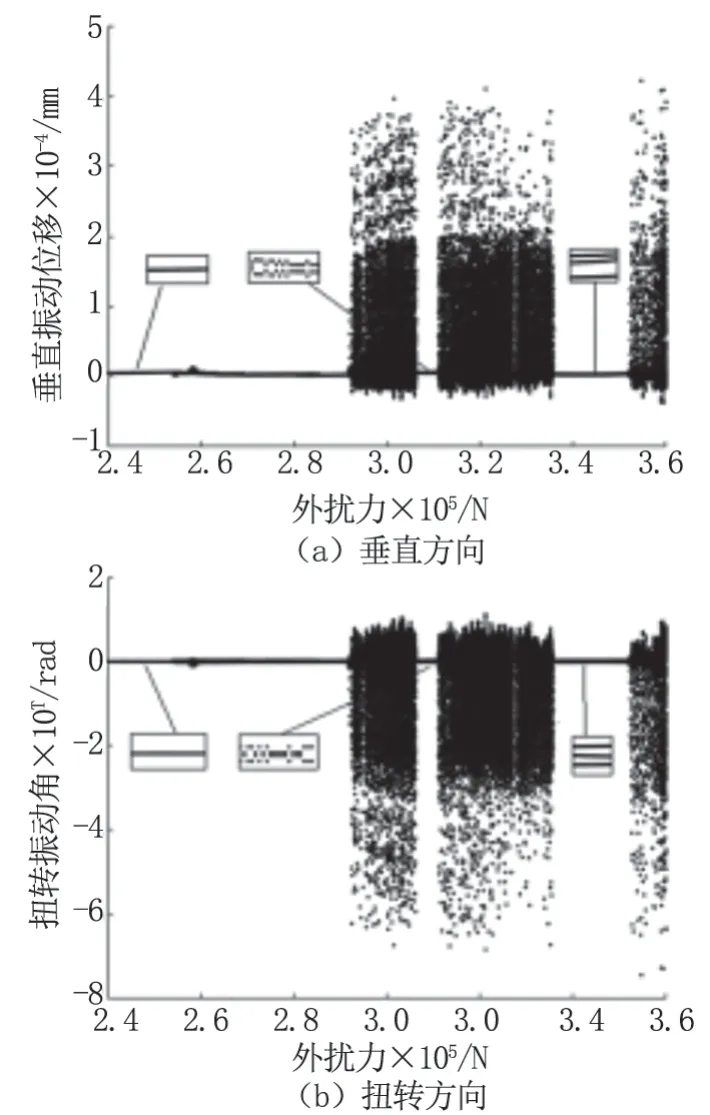
图5 外扰力F0 变化下轧机的局部分岔图

5 结语

本文采用多尺度法，利用四辊轧机垂直—扭转耦合振动动力学模型，再结合实际轧机工作参数，研究在不同参数变化情况下的四辊轧机垂直震动及扭转震动呈现出的不同状态，例如，外扰力化时轧机主共振幅频，F0 值为2.495×105N、3.081×106N、3.235×105N 时轧机的状态。以期能够为研究解决轧机震动问题提供参考。