扩散磁共振图像的大脑微结构成像研究综述

朱悦敏,王远军

(上海理工大学 医学影像技术研究所,上海 200093)

1 引 言

扩散磁共振成像(Diffusion Magnetic Resonance Imaging,dMRI)是在磁共振基础上发展起来的一项技术,可以通过水分子扩散运动的各向异性来显示大脑组织的微结构图像.同时,它也是目前唯一对人脑白质微观组织结构进行非侵入性检测的方法,能够在活体内表征人脑的组织微结构特性.近年来,针对扩散磁共振成像的研究层出不穷[1-7],该技术已被广泛应用于神经科学研究和临床应用中.扩散张量成像[8](Diffusion Tensor Imaging,DTI)是最早被提出用来估计纤维方向分布的扩散磁共振成像技术,该技术利用扩散张量(Diffusion Tensor,DT)模拟水分子的扩散,将DT表示为一个对称正定矩阵,即:

(1)

D的对角线对应于沿3个正交轴的表观扩散系数(Apparent Diffusion Coefficient,ADC),而非对角线单元表示沿这三个正交轴的位移之间的相关性.扩散张量的对角化产生特征值(λ1、λ2、λ3)及其向量(e1、e2、e3),可表示为以下形式来描述沿主扩散轴的方向和表观扩散系数,即:

(2)

该模型不仅简单且所需采样方向少,已成为临床诊断中的常用方法.然而,DTI只能描述每个体素中的单一纤维方向,无法对图1所示的交叉、弯曲、分叉等复杂纤维进行描述.此外,它所提供的非特异性参数例如分数各向异性(Factional Anisotropy,FA)和平均扩散系数(Mean Diffusivity,MD)也不能区别体素内不同组织微结构特征.

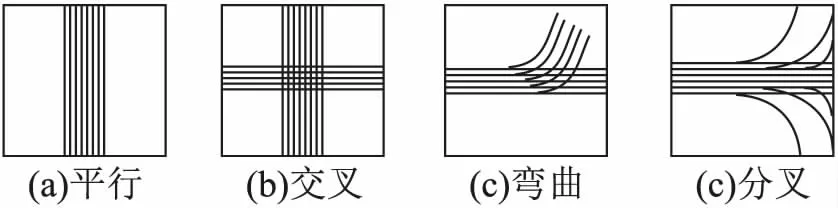
图1 纤维结构取向

针对DTI的不足,研究者从信号模型、多隔室模型两个分支展开了很多研究,分别用来表征单体素内纤维的多方向性以及描述特定类型组织的微结构.信号模型方法的研究基于高角度分辨率扩散成像[9](High Angular Resolution Diffusion Imaging,HARDI),包括扩散谱成像[10](Diffusion Spectrum Image,DSI)、Q-ball成像[11](Q-ball Imaging,QBI)、球面反卷积[12](Spherical Deconvolution,SD),其主要思想是通过描述扩散加权衰减信号来获得多纤维方向信息,然后寻找最优纤维路径以重构脑神经纤维.在多隔室模型中,每个隔室对应于特定的细胞成分,通过将多隔室模型与MR信号相拟合来获得相应成分的微结构参数.目前已有的多隔室模型包括球棍模型[13]、复合受阻受限扩散模型[14](Composite Hindered and Restricted Model of Diffusion,CHARMED)、AxCaliber[15]模型、ActiveAx[16]模型、轴突取向弥散和密度成像模型[17](Neurite Orientation Dispersion and Density Imaging,NODDI)、扩散基谱成像[18](Diffusion Basis Spectrum Image,DBSI)、胞体和轴突密度成像模型[19](Soma and Neurite Density Imaging,SANDI)等,这一类方法通过开发将MR信号与生物物理建模相结合的定量技术来解码扩散加权信号中包含的信息,最终目标是从扩散磁共振图像中获得更精细的大脑微结构信息.

近几年来,微结构成像方面的研究取得了一些进展,其中包括:估计单个体素中多纤维方向、精准分辨交叉纤维束、提高角度分辨率并减少伪影、获得神经突的形态学量化参数等.但同时也存在很多局限性:多隔室模型的假设过于简单化、理想化,忽略了组织结构的真实形态和细节;扩散数据采集耗时过长,难以应用于临床;目前缺乏受到广泛认可的模型能够将多种对比度的组织特征联系起来进行定性与定量分析.

本文首先介绍扩散磁共振成像的基本原理,然后从多隔室模型与信号模型两个角度综述了经典的大脑微结构成像方法和最新研究进展,阐明这两类模型存在的优点及其局限性,接着介绍微结构量化分析方法,最后对微结构成像技术进行总结和展望,具体框架见图2.

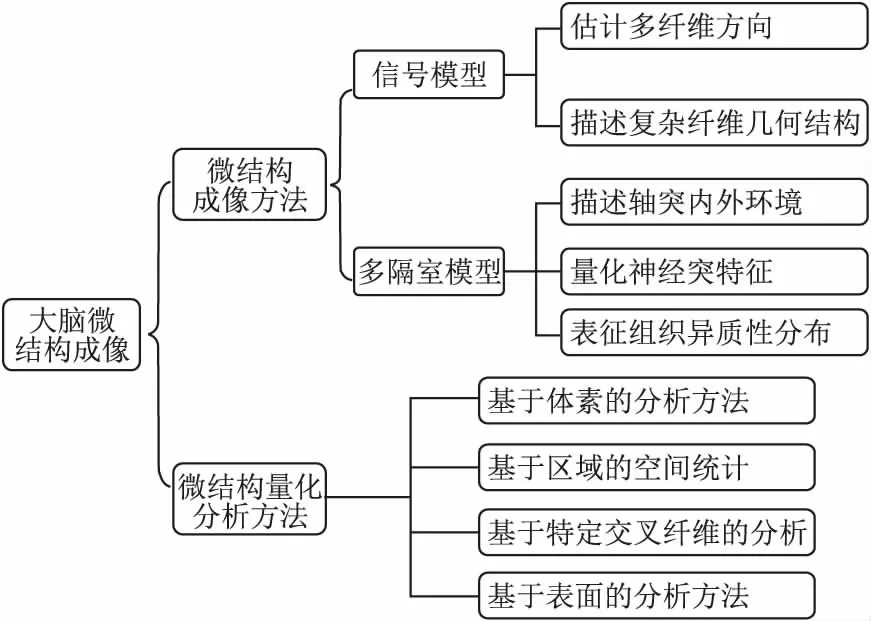
图2 大脑微结构成像研究框架

2 微结构成像

随着MRI扫描技术的不断改进以及HARDI对多壳数据快速采样策略的发展,新的微结构成像方法正不断涌现.本文主要介绍两类主要的微结构成像方法,即信号模型与多隔室模型.信号模型包括表征复杂纤维结构的先进的dMRI技术,通过概率密度函数或纤维分布函数来描述衰减信号;多隔室模型则把信号与脑组织微观特征直接联系起来,通过将这些特征建模为简单的几何对象来提供对信号的解析或数值近似,从而能够通过数值拟合估计特定的微观特征,并提供与神经科学应用相关的神经元特征的估计,例如轴突直径、纤维密度与方向等.这些模型的创新主要在多纤维方向、复杂纤维结构、轴突内外环境、神经突特征等领域.

2.1 信号模型

2.1.1 估计多纤维方向

为了弥补DTI模型在单体素中仅能估计一个纤维方向这一不足之处,需要建立新的模型来重建纤维方向分布函数(Orientation Distribution Function,ODF)以提供更完整的多纤维走向信息.使用SD直接从MRI测量中重建ODF是目前最常见的方法,这种方法的主要思想是假设整个大脑具有相同的扩散特性,用信号响应函数来表示单个纤维上的扩散加权信号衰减,多根纤维的扩散信号衰减则看作是每个纤维方向上的信号响应函数与纤维方向分布函数在球面上的卷积.然而,基于SD的方法对噪声十分敏感,为了减少该技术对噪声的敏感度,一系列正则化技术被引入到SD方法中[20].其中,Tournier等人[21]引入了Tikhonov正则化对ODF的负值施加约束,称为约束球面反卷积(Constrained Spherical Deconvolution,CSD)模型,该模型克服了扩散张量模型固有的交叉纤维限制,在ODF估计中表现出较高的重建精度.在CSD模型的基础上,岳晴等人[22]提出了NLCSD模型,利用分数阶正则化和邻域信息来代替CSD模型的整数阶正则化,使得模型解更接近真实解.在ODF重建中,该方法能够进一步准确、完整地重建出每个体素中的多纤维方向;在后续纤维追踪的结果中,NLCSD呈现出较好的视觉效果及较高的准确率.针对MRI扫描时出现的部分容积效应会影响脑区多纤维区域走向估计这一现象,潘映钰等人[23]结合DTI、DKI、NODDI多种扩散模型提出一种基于多模型响应函数的CSD方法,以衰减大脑白质中的各向同性扩散信号,克服容积效应带来的影响,提供更加准确的多纤维方向信息.随着多壳数据逐步应用于微结构成像研究中,Jeurissen等人[24]将CSD模型应用于多壳数据上,提出了多壳多组织约束球形去卷积(Multi-shell Multi-tisse Constrained Spherical Deconvolution,MSMT-CSD),如图3所示,MSMT-CSD将扩散MRI信号分解为灰质(Gray Matter,GM)、白质(White Matter,WM)和脑脊液(Cerebrospinal Fluid,CSF)区,利用不同组织类型的扩散敏感度相关性来估计ODF,与CSD相比,MSMT-CSD可以显著提高ODF定向的精度,并减少含有GM或CSF的体素中伪峰的存在.除了能够区分多种组织类型,提高ODF估计的精度外,MSMT-CSD获得的WM、GM、CSF体积分数图也可以用于改善脑部扩散纤维束成像[25]并评估白质纤维束形态[26],判断纤维跟踪终止区域及纤维结果是否合理.还有研究[27,28]将MSMT-CSD模型从传统线性扩散编码数据推广到具有任意b张量形状(如球面、平面)的张量值扩散编码,采用非常规梯度波形在多个方向上进行扩散编码,从张量值扩散编码数据中估计纤维ODF和信号分数,这类方法表明,不同形状的扩散编码数据的组合能够更好地区分WM和GM.

图3 MSMT-CSD与CSD模型估计ODF

一般而言,扩散加权强度越高的数据具有更高的角度分辨率,但也通常伴随着信噪比降低这一特征.为了解决这一问题,阻尼Richardson-Lucy模型(Damped Richardson-Lucy,DRL)[29]将Richardson-Lucy球形反卷积算法与自适应正则化技术相结合,使用纤维取向的绝对动态范围来调制解的正则化,该方法能够抑制部分体积效应导致的虚假纤维方向分布峰值,并防止对噪声的过度拟合.为了进一步提高估计精度,DRL的改进框架——广义Richardson-Lucy模型(Generalized Richardson-Lucy,GRL)[30]通过考虑代表不同组织类型的信号模型来提高WM ODF的重建精度,并在后续纤维追踪成像过程中使用信号分数图来代替追踪过程中定义的纤维方向分布阈值,提供了更高质量的纤维终止准则.

除了对WM ODF估计的研究外,近年来越来越多的研究关注了球面去卷积对GM组织的适用性.由于GM在扩散过程中具有显著的各向异性特征,Luca[31]引入了多样纤维方向分布框架(Multiple Fiber Orientation Distributions,mFOD)来实现多个各向异性响应函数的球面反卷积,改善了GM中ODF的重建,使得纤维方向估计能够同时在WM和GM中实现.

2.1.2 描述纤维几何结构

神经纤维是大脑传递信息的重要媒介,为了满足各类信息传递的需求,纤维往往以复杂的几何结构连接不同脑区.然而,对于弯曲、交叉和分叉等结构,DTI无法描述它们的纤维取向.为了描述纤维几何结构与走向规律,已在dMRI技术基础上研发了一些新方法.

DSI[10]使用多b值多方向的扫描序列,采集水分子在整个Q空间的弥散信息,得到每个体素内的分子位移分布,从而提取出组织的微观结构信息并进行几何特征测量.然而,DSI模型的采样时间成本相对较高,难以应用于临床.因此,相关研究通过使用径向对称的Q空间DSI采样方法[32]或融入压缩感知理论[33]来缩短采集时间,同时提高了重建方向分布函数的角分辨率和精度.罗伶俐等人[34]基于径向基函数(Radial Basis Function,RBF)方法提出对信号进行自适应衰减建模的方法,并对扩散张量的求解方式进行改进,不仅提高了DSI中扩散信号的重建准确率,而且大大缩短了重建时间,减少了计算负担.为了解决采样时间长这一问题,QBI[11]提出新的采样方法,不同于传统DSI使用矩形网格对扩散编码空间进行采样,而是在一个足够大的球体上遍历Q空间(如图4所示),用相比DSI更少的弥散编码方向获得神经纤维几何结构与走向信息,减少扫描时间.

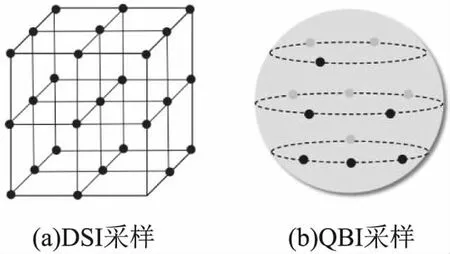
图4 (a)DSI采样;(b)QBI采样

传统的纤维ODF估计方法利用对称纤维分布函数假设体素中的纤维轨迹近似于纤维取向分布的主方向,但在复杂的纤维结构区域中,弯曲、交叉的纤维被证明其实并不全对称.为了解决纤维形状不对称问题,研究者们尝试使用非对称纤维取向分布函数来描述复杂纤维几何结构.非对称ODF估计的主要思想是在拟合中加入邻域连续性分量,将来自相邻体素的信息合并到纤维估计中,施加纤维连续性约束来解析不对称的纤维模式[35].Wu等人[36]将不对称ODF估计应用DSI,提出了不对称光谱成像(Asymmetry Spectrum Imaging,ASI),可以表征复杂的亚像素纤维结构并得到较准确的估计结果,对发育中的大脑进行有效的脑纤维束成像.最近的研究发现,在浅表白质处实现纤维跟踪算法时,估计的纤维轨迹倾向于终止于脑回冠而不是脑沟壁.这种潜在的回旋偏差可能会影响创建准确的大脑连接图,Wu和Schilling使用不对称纤维取向分布函数来减轻浅表白质的脑回偏差影响[37,38],使脑回叶处的纤维流线能够更平滑地进入皮层,改善了皮质之间的连接性.

2.2 多隔室模型

在多隔室模型微结构扩散成像中,DW信号被建模为不同隔室的贡献之和.标准的多隔室模型包括两个隔室,用来模拟来自轴突内和轴突外水分子的信号,有时可以以第3个隔室为特征来描述脑脊液的部分体积效应,不同模型的区别在于模型中包括的隔室数量以及为捕捉每个隔室的显著扩散特征而做出的假设(即模型约束).建立扩散磁共振多隔室模型的主要目标之一是提高病理特异性,如表1列举的各个经典多隔室模型主要测量参数所示,一些先进的多隔室模型可以对特定微观组织提供有用的非侵入性描述.利用先进的弥散磁共振成像技术估计脑的微结构特征,将为理解脑成像与临床表现之间的关系提供新的见解.下文将对经典的多隔室模型及其最新进展进行详细介绍.

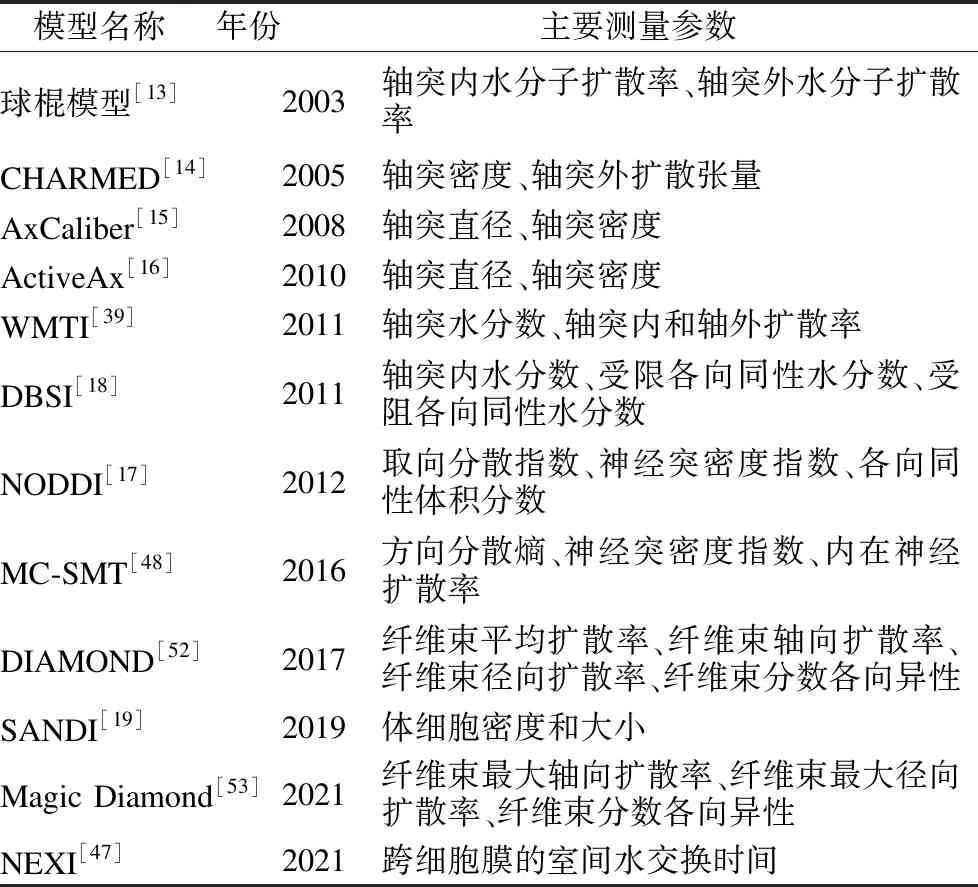
表1 多隔室模型主要测量参数

2.2.1 描述轴突内外环境

2003年,Behrens等人[13]提出球棍模型来描述轴突内、外环境.该模型假设轴突内和轴突外环境具有相同的扩散率,将轴突内环境表示为半径为零的平行圆柱体,水仅沿柱轴方向扩散;而轴突外环境的扩散则表示为遵循各向同性扩散的张量模型.随后,Assaf等[14]在此基础上提出了CHARMED,它分别用受限扩散和受阻两种扩散模式来描述轴突内环境与外环境,轴突内使用沿多个纤维方向的半径服从伽马分布的圆柱体建模,轴突外采用扩散张量建模.该模型拟合出的参数包括受限体积分数、受限纤维取向和受阻隔室的表观扩散系数,但它需要耗时的扩散采集来提供对隔室组织结构的稳健估计.

另一类两室模型聚焦于平行排列的纤维束组成的WM区域,提出了白质束完整性模型[39](White Matter Tract Integrity,WMTI),该模型提供了轴突内外扩散张量的解析表达式并量化轴突含水率,并根据表观扩散张量和峰度张量解析计算得到轴突内与轴突外的扩散系数和轴突内体积分数,利用线性最小二乘进行估计避免对多指数模型进行耗时的非线性拟合.更新颖的模型如Lemonade[40]采用类似的方法在给定b值扩展系数的情况下分析估计组织参数,但考虑了更高阶的扩展.一般来说,WMTI或Lemonade方法能够在有限的拟合约束下计算生物组织参数,但由于需要较长的采集时间实现高阶张量的估计且容易产生测量误差,通常难以在临床环境中实施.

2.2.2 量化神经突特征

为了更精确地量化神经突特征,一部分技术着重于实现神经突密度和方向变化的估计.AxCaliber[15]在CHARMED模型上进行扩展,引入轴突直径分布(Axon Diameter Distribution,ADD)这一概念,将轴突建模为一组具有不同直径的圆柱体的水分子扩散模型,以估计神经束内轴突直径分布[41].然而,后续的研究表明AxCaliber没有考虑到轴突取向的分散性,因而可能导致体素内的轴突直径分布量化产生偏差.为了克服这一限制,Alexander等人提出了ActiveAx[16]技术,该方法将扩散信号描述为受限、受阻和各向同性扩散隔室的贡献总和,利用大量高质量的DWI数据来估计轴突内和轴突外的体积分数和轴突直径,其估计效果与梯度强度密切相关,当使用超高梯度强度采集时,所获得的轴突直径指数与组织学成像方法相当,但采用低梯度强度的PGSE序列成像对小直径的轴突成像不敏感.到目前为止,由于数据分析的复杂性,这两类方法主要应用于科学研究中.

除了早期的二室模型外,部分三室模型用于量化神经突特征.2012年,Zhang等人[17]提出了在临床上更具可行性的NODDI模型,由于可以通过临床上的成像方法来量化GM与WM的微观结构变化,NODDI在神经影像学领域得到了迅速发展,如图5所示该模型包括包含细胞内、细胞外和脑脊液3个隔室,由扩散信号估计出一系列微观结构参数用来反映轴突密度和神经方向变化等.与DTI衍生指数相比,NODDI参数已被证明是更具体的组织损伤指标,并与多发性硬化症的各种组织病理过程显著相关.但最近有研究表明,NODDI对组织微结构做的假设并不适用于整个大脑.Kleban等人[42]发现,NODDI将整个大脑的神经扩散率的值固定为1.7,并对轴突外的垂直扩散率采用曲折模型,可能会导致错误地反映微观结构变化.针对这一问题,Veraart等人[43]提出使用回波时间作为额外的测量参数;Coelho等人[44]使用线性和平面张量编码的结合改进了模型中的参数估计.

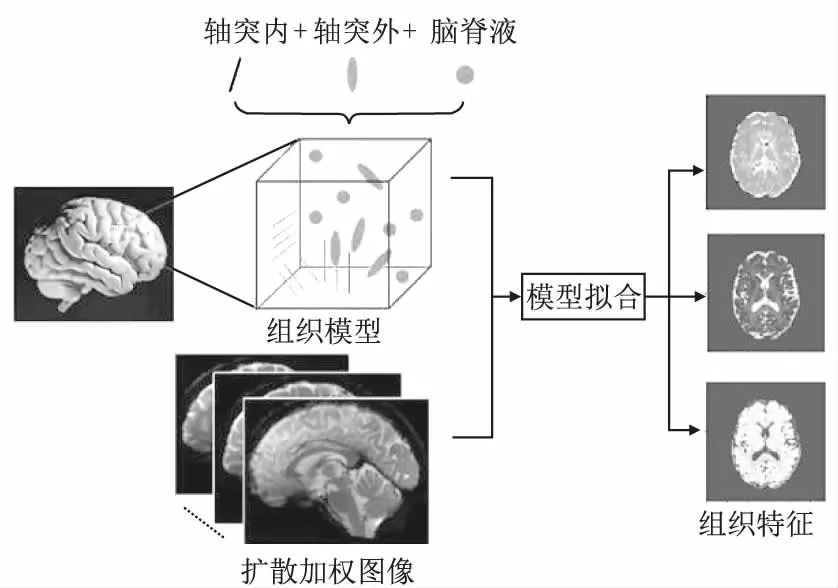
图5 NODDI三隔室模型

尽管NODDI有效提高了可临床性,但有研究发现NODDI在GM中对于部分指标例如神经突密度指数(Neurite Density Index,NDI)的估计不可靠,这表明NODDI更适用于用来获得WM中的微结构特征.同时,最近的研究表明,传统的二室模型也不能很好地表示GM信号[45],这可能是由于它们忽略了细胞内和细胞外隔室以及不同细胞内隔室之间发生的水分子交换过程[46].由此,为了建立能够描述GM微结构特征的模型,Palombo等人[19]拓展了多隔室模型在GM中的应用并提出了SANDI模型,该模型首次将细胞体大小和密度与轴突密度结合在一起,从而能够使用dMRI和基于多隔室模型的方法无创地进行GM微结构估计,该方法将体细胞明确建模为细胞内信号的贡献之一,假设出一个用于分离和量化胞体的三室模型:细胞外空间和轴突隔室都遵循标准模型分别建模为各向同性的高斯分布和细长圆柱体,胞体内隔室建模为封闭的球体,根据MR测量的球形隔室大小和相对信号分数提供胞体大小和密度图.除了SANDI模型,最新的一项关于GM的扩散MRI多隔室研究提出神经突交换成像(Neurite Exchange Imaging,NEXI)[47]作为灰质微结构映射的最小模型,该模型没有像SANDI一样将胞体作为第3个隔室,而是在神经突和细胞外空间这两个隔室的各向异性模型上描述灰质中扩散信号并解释这些信号特征,结果表明NEXI比具有体细胞的三室模型更适合于在扩散时间t>20ms时表征皮质微观结构.

NODDI的另一个问题是它使用单一的Watson分布描述轴突的取向分布,从而没有考虑到纤维交叉带来的影响.针对这个问题,Kaden扩展了基于球面平均技术的微观扩散各向异性成像,引入了多室球面平均法[48](Multiple Compartment Spherical Mean Technology,MC-SMT),目的是绘制不受纤维交叉和取向分散影响的轴突密度和特定隔室的显微扩散系数.这种多室微观模型克服了现有技术中的关键限制,不对轴突取向分布做出任何假设,从数据中估计微观扩散系数,提供了NDI、内在神经扩散系数和方向弥散熵(Orientation Dispersion Entropy,ODE)信息[49].

2.2.3 表征组织异质性分布

除了描述轴突内、外环境以及神经突特征,还有一部分模型用于表征组织异质性分布.DBSI[18]将轴突外空间建模为各向同性扩散张量谱,由扩散系数函数定义各向同性张量的相对分数,通过多个各向异性和各向同性扩散张量的线性组合来描述扩散中体素内的组织异质性.DBSI模型假设轴突内和轴突外的隔室之间没有成分交换,并且将各向同性扩散模式与其他隔室分开,以区分细胞组织内的扩散、血源性水肿和CSF内的非限制性扩散.受限光谱成像[50](Restriction Spectrum Imaging,RSI)通过分离受阻扩散和受限扩散的体积分数和取向分布,获取传统DSI重建所不能提供的结构信息.

Ning等人[51]利用扩散扰动函数来表示扩散率的变化程度,从该扰动函数中推导出短期和长期扰动系数,以表征组织异质性分布.

Scherrer等人[52]提出三维各向异性微结构分布隔室(Distribution of Anisotropic Microstructural Environments in Diffusion Imaging,DIAMOND)用来表征扩散室成像中三维各向异性微结构环境的分布,该模型通过混合扩散张量的连续分布来分解体素内的组织室,获得亚体素分辨率级别的微结构特性.DIAMOND改善了DTI具有敏感性但缺乏特异性的特点,可以用来表征体素内的定向异质性以及每个组织室的三维扩散率.之后,在传统DIAMOND模型基础上,Magic Diamond[53]采用张量值编码产生平面或球形编码新序列代替单一方向的线性编码,然后从张量值扩散编码产生的互补扩散信息中估计扩散张量的空间分布.实验中发现,这种将线性扩散编码和平面或球形扩散编码相结合的方式能够使Magic Diamond模型参数估计更加稳健.

3 微结构量化分析方法

为了进一步量化大脑微结构特性,研究者提出了一系列针对灰质和白质的量化分析方法,表2列举了这些方法的分析范围、特异性以及关键策略,下文将对这些方法一一介绍.

表2 微结构量化分析方法

3.1 白质微结构量化分析方法

白质微结构量化分析方法主要可分类为基于体素的分析[54](Voxel-Based Analysis,VBA)、基于区域的空间统计分析[55](Tract-Based Spatial Statistics,TBSS)以及基于体素内特定交叉纤维群体的分析[26](Fixel-Based Analysis,FBA).

VBA的主要思想是通过将不同对象的FA图像配准到公共空间以进行逐体素的统计分析,由于该方法对所采用的平滑和配准技术较为敏感,因此易导致结果精度不足;此外,VBA不能提供关于纤维取向的信息,也不能处理交叉纤维的扩散量.为解决VBA在平滑及配准技术上的困难,Smith提出了TBSS框架.该方法创建平均FA骨架图像来表示所有纤维束的中心,将所有受试者配准后的图像投影到白质纤维束骨架上,然后对骨骼体素进行跨受试者的体素统计分析.与VBA方法相比,TBSS不需要进行空间平滑处理,也减少了对图像配准精度的要求.然而,由于DTI的相关固有限制,TBSS也不能估计和解释纤维交叉区域的体素统计,并且其分析仅限于骨架体素,忽略了其他WM区域.Raffelt等人提出的FBA进一步解决对交叉纤维等复杂纤维结构的描述,该方法依赖于WM纤维取向分布,将受试者纤维取向分布图像配准、变形并重新网格化到公共模板空间.FBA是一种用来评估大脑白质纤维束形态学的方法,具有比体素层面的测量更具特异性的优点,能够在存在交叉纤维群体的情况下分析单个纤维的特定特性,并且可以比较任何纤维方向上与体素内轴突总体积相关的度量.对于Fixel的测量参数指标包括白质微结构的表观纤维密度(Apparent Fiber Density,AFD)、表征宏观差异的纤维束截面(Fiber-bundle Cross-section,FC)与纤维密度截面(Fiber Density and Cross-section,FDC),这些参数指标可用于在组比较中区分不同的、特定的纤维束群的变化[56].通过与其他分析方法联合使用,可以从宏观和微观的角度对白质结构特性进行全面的评估.目前,FBA研究的核心工具已作为MRtrix[57]软件包的一部分在各类临床研究中广泛使用.

3.2 灰质微结构量化分析方法

对于灰质的结构量化分析方法除了VBA,还包括基于灰质的空间统计[58](Gray Matter Based Spatial Statistics,GBSS)和基于表面的分析[59](Surface Based Analysis).GBSS是用于分析GM扩散指数的基于区域的空间统计方法,在这一方法中,具有最高GM部分体积附近的体素被投影到骨架化的平均GM概率图上,减轻了部分体积效应的影响,进一步提高了受试者之间的配准精度.基于表面的分析通过利用大脑皮层表面的自然几何形状和非解剖皮质特征进行表面配准,基于GM微观结构特性的层特异性执行基于层的分析并评估扩散指标相对于皮层表面法线的方向性[60,61].

4 总结与展望

大脑微结构成像方法对脑神经科学研究和中枢神经系统疾病诊断和治疗具有十分重要的意义,为组织微结构的无 创检测提供了可能,因此近年来该技术广受关注,许多学者提出了多种不同的算法及优化模型,目前已被广泛应用于神经系统疾病的临床应用研究中.考虑到微结构成像现有研究的不足,未来该方向的研究以下方面值得重点关注:

1)尽管多隔室模型提高了扩散成像的病理特异性,但目前常用的生物物理模型仍然是对潜在神经组织特性的过度简化,例如轴突通常被建模为不同半径的密集圆柱体,但显微技术表明轴突真实形态实际上更为复杂,因此生物物理模型应尽可能地精细化以接近实际组织微结构的真实形态,才可能发挥关键作用将dMRI研究转化为临床实践.

2)由于dMRI的数据和实际神经元的微米尺度相差过大,所得到的微结构信息只能进行定性描述,要使得这一技术得以推广,应将微结构模型得到的参数指标进行可靠的生理学验证.目前的显微镜技术已经能够很好地表征多隔室模型的各个构建模块,因此,相关的显微镜技术可以与dMRI领域相结合使用,以弥合全脑体内微观结构估计与离体薄组织切片的电子显微镜图像之间的差距.

3)当前存在的各种模型都只适用于特定类型的组织,例如单个白质束、皮层、胶质母细胞瘤等,尚未开发出一种适用于大脑任何区域的标准模型,因此研发一个具有高b值的多壳多个扩散时间以及不同扩散张量编码方案的统一大脑微观结构模型对于增加临床实用性有重要意义.