基于熵产理论和响应面法的轴流式止回阀结构优化设计
李金铭,邹淑云,刘 忠,喻哲钦,李志鹏,邵建农
(1.长沙理工大学 能源与动力工程学院,长沙 410114;2.远大阀门集团有限公司,河北邢台 055350)
0 引言
轴流式止回阀凭借优良的启闭性能在工业领域得到了广泛的应用[1]。然而,目前轴流式止回阀在结构设计上仍存在一些不足,从而导致阀门内部存在较多漩涡,其整体能耗偏大,流动性较差。因此,对其内部结构进行优化设计,降低能量损失,提升其流通性能显得极为重要。
张立强等[2]利用椭圆簇法对轴流式止回阀导流体和流道形状参数进行了优化。李科良等[3]运用汇源法对轴流式止回阀结构进行了优化,研究了阀门内部流场的压力特性和流量特性。余建平等[4]采用分离转捩模型对轴流式止回阀进行了优化,发现光滑渐扩型流道阻力较小,具有很好的流通性。但以上研究主要是参考流线型设计,通过分析阀门内部压力分布、速度分布等特性对阀门进行优化,并未深入分析阀门内部能量损失机理。
熵产能直观地反映能量损失发生的位置且准确得出其损失大小,近年来在流体机械领域得到了很好的应用。张帆等[5]通过数值模拟对侧流道泵进行熵产分析,发现泵内部的流动损失主要与湍流耗散熵产有关。LI 等[6]基于熵产理论分析了水泵水轮机泵工况下的水力损失详细分布。YU 等[7-9]通过对水轮机的数值模拟发现,尾水管内熵产较大,且熵的形成主要是由漩涡、流动分离和回流等流体动力因素引起。在运用熵产理论进行优化设计方面,宋科等[10]采用熵产理论分析了导管桨工作时内部的流动损失状况,通过添加毂帽鳍对导管桨进行了优化改进。GHORANI 等[11]为使反向泵减少熵产,对反向泵的叶片形状和数量以及流道入口宽度进行了优化,提高了水力效率。王威等[12]将最小熵产作为目标,结合优化算法对叶栅型线进行了优化,减少了能量损失,但是优化算法无法直观地判断因素变化与目标值的关系。
响应面优化法相比于正交优化和优化算法,具有不局限于正交试验中的最优解并能形象描绘因素与目标值关系的优点。王同等[13]以喷管数量、喷管直径和风管数量为试验因素,采用响应面试验法对风道结构进行了优化。何坤健等[14]采用数值计算和响应面法得到了圆盘泵叶片数量、叶片高度以及盘间距的最佳参数,使得优化后的圆盘泵效率明显提升。
鉴于鲜有将熵产理论用于阀门结构优化设计的研究及响应面法的优越性,本文提出结合熵产理论和响应面法的轴流式止回阀结构优化设计方法,并应用于DN100 轴流式止回阀结构优化设计中。以能量损失最小为目标,结合计算流体动力学和统计学方法得到最优结构参数,并对优化前后轴流式止回阀的熵产和流场进行对比分析。
1 模型数值计算
1.1 熵产理论
雷诺时均湍流流场中的熵产主要包括因时均速度场引起的直接耗散熵产和因脉动速度场引起的湍流耗散熵产[15]。由于研究对象内部水的温度基本不变,因此不考虑传热引起的熵产。总熵产值为直接耗散熵产与湍流耗散熵产之和,见式(1):
式中,S,S1,S2分别为总熵产、直接耗散熵产、湍流耗散熵产,W/K;S11为直接耗散熵产率,W/(m3·K);S22为湍流耗散熵产率,W/(m3·K);分别为时均速度在x,y,z 方向的分量,m/s;u',v',w'分别为脉动速度在x,y,z 方向的分量,m/s;μ为流体动力黏度,Pa·s;T 为温度,K。
由于式(5)无法直接得到,且KOCK 等[16-17]研究发现脉动速度引起的熵产和湍流模型有一定联系,S22可表示为:
式中,ρ为流体密度,kg/m3;ε为湍动能耗散率。
1.2 轴流式止回阀模型及结构参数设计
轴流式止回阀主要由阀体、阀瓣、导流罩、弹簧和阀杆组成,如图1 所示。对轴流式止回阀进行优化设计,其内部主体结构参数如图2 所示。

图2 轴流式止回阀结构参数Fig.2 Structural parameters of axial flow check valve
图2 中,阀体入口角为圆弧P1P2过点P1的切线与水平线的夹角,导流体结构形状可由Myring方程描述,见下式:
式中,R0,Rmax,L1,L2分别为导流体半径、导流体最大半径、阀瓣宽(OP3长度)、导流罩长(OP5长度),mm;阀瓣P3P4外形由前半段函数描述,m 为阀瓣形状参数,用来调节阀瓣形状;导流罩P4P5外形由后半段函数描述,θ为阀芯尾角,用来控制导流罩外形曲线P4P5与线段OP5在点P5形成的夹角。
为了保证设计的合理性,阀体流道半径可由式(8)表示。其余部分通过圆弧光滑连接。
式中,r,r0分别为流道半径、喉口半径,mm。
1.3 数值计算
本文优化对象为DN100 轴流式止回阀,利用三维建模软件对轴流式止回阀进行建模。在阀门进、出口分别添加5 倍管径长和10 倍管径长的管道,对模型内部流体域进行抽取;采用网格划分软件对流体域模型进行四面体网格划分(见图3),通过计算流体动力学软件进行数值计算。流体介质为温度293.15 K 的水,入口速度取4.0 m/s,以保证阀瓣全开。计算模型采用Realizable k-ε模型[18],默认压力出口。压力与速度的解耦采用SIMPLEC 算法,压力项采用标准格式离散,控制方程其他项均采用二阶迎风格式以保证精度。经网格无关性检验,网格数量保持在260 万以上。由计算可得此时流阻系数为3.78,与同直径轴流式止回阀试验结果(流阻系数为3.60)相近[19],误差在5%以内,说明数值模拟结果可靠。为保证优化设计的合理性,后期所有试验结果均采用以上设置条件通过数值计算获取。

图3 流体域网格Fig.3 Meshing of fluid domain
2 优化试验设计
2.1 Plackett-Burman 试验设计
Plackett-Burman 试验设计原理是选取因素的高水平(+1)和低水平(-1)进行试验设计,利用统计学方法对比分析高、低水平因素差异与试验整体差异之间的关系,高效地筛选出对试验结果有显著影响的因素。
Plackett-Burman 试验设计法可针对试验因素较多不便于后续研究的情况,筛选出对试验结果有重要影响的因素,以减少研究的工作量。
2.2 最陡爬坡试验
最陡爬坡试验原理针对筛选出来的显著性因素,以其试验值变化的梯度方向为爬坡方向,根据其效应值的大小确定变化步长,分析试验因素与试验结果的变化规律,从而缩小试验因素的优化范围。最陡爬坡试验可使前期试验筛选出来的显著性因素快速接近最优范围,提高优化结果的准确性。
2.3 Box-Behnken 响应面法试验设计
2.3.1 响应面法原理
响应面法原理主要根据实际需要设计合理的试验[20-22],并对试验结果进行多元回归拟合,得到响应值g 和设计变量a 的数学模型,见下式:
式中,y0(a)为目标函数;δ为总误差。
y0(a)主要有一次型和二次型,分别如下所示:
式中,β为待定系数;n 为变量个数。
2.3.2 响应面试验设计
响应面设计分为中心复合设计和Box-Behnken 设计。后者具有简单、因素及水平设置相同时试验次数少、无试验因素均为高水平(+1)的试验情况和试验结果可靠等优点,故本文采用Box-Behnken 响应面试验设计。
轴流式止回阀结构优化设计流程如图4 所示。

图4 轴流式止回阀结构优化设计流程Fig.4 Optimization design flowchart of axial flow check valve structure
3 结果与分析
固定导流体最大半径Rmax=40.0 mm 和喉口半径r0=35.0 mm,以保证导流体的安装以及阀瓣的正常启闭,为优化试验做铺垫。
3.1 Plackett-Burman 试验结果
对入口角、阀瓣宽、阀瓣形状参数、导流罩长和阀芯尾角5 个因素进行Plackett-Burman 试验设计,以总熵产值为筛选指标,筛选出显著影响因素。Plackett-Burman 设计因素与水平见表1,试验结果见表2。

表1 Plackett-Burman 设计因素及水平Tab.1 Factors and levels of Plackett-Burman design

表2 Plackett-Burman 试验结果Tab.2 Results of Plackett-Burman experiment
对表2 试验结果进行方差分析,结果见表3。模型P <0.01,决定系数R2为0.941 3,调整确定系数RAdj2为0.892 4,与决定系数相近,说明模型可靠,能进行下一步分析。其中,极显著性因素为X1,X5(P<0.01);显著性因素为X2(0.01<P<0.05);非显著性因素为X3,X4(P>0.05)。故选取入口角、阀瓣宽和阀芯尾角进行下一步优化,并通过单因素分析将阀瓣形状参数确定为1.5,导流罩长确定为116.8 mm,以便后期优化。

表3 Plackett-Burman 试验结果方差分析Tab.3 ANOVA results of Plackett-Burman experiment
3.2 最陡爬坡试验结果
对入口角、阀瓣宽和阀芯尾角3 个因素进行最陡爬坡试验,试验设计和结果见表4。

表4 最陡爬坡试验设计和结果Tab.4 The path of steepest ascent design and results
由表4 可知,随着阀瓣宽和阀芯尾角增大,入口角减小,压力损失呈现先减小后增大的变化。当入口角为26.3°,阀瓣宽为22.5 mm,阀芯尾角为30.0°时压力损失最小,说明此时阀门内部能量损失最小,最优结构参数存在于2 号试验因素水平附近。因此,以表4 中2 号试验的3 个因素水平为中心值设计后续响应面试验。
3.3 Box-Behnken 响应面法试验结果
以入口角、阀瓣宽和阀芯尾角为自变量,总熵产值为响应值,进行Box-Behnken 响应面试验。试验因素和水平见表5,试验结果见表6。

表5 Box-Behnken 试验因素及水平Tab.5 Factors and levels of Box-Behnken experiment

表6 Box-Behnken 试验结果Tab.6 Results of Box-Behnken experiment
对表6 中的结果进行二元回归拟合,得到总熵产值的回归方程:
对式(12)进行方差分析,结果见表7。

表7 Box-Behnken 回归模型方差分析Tab.7 ANOVA for Box-Behnken quadratic model
由表7 可知,本模型F 值为94.48 且P <0.01,失拟项P >0.05,表明模型的可信度极高;决定系数R2=0.991 8,调整确定系数RAdj2=0.981 3,说明模型可以较为准确地预测响应值,有利于后期优化分析。
绘制回归方程的响应面图(见图5~7)。响应面图中的因素坡度越陡,说明该因素影响越大;反之,坡度越平缓,则说明该因素影响越小。由图5~7 可知,入口角和阀芯尾角为定值时,阀瓣宽增加,总熵产值先减少后增加;阀瓣宽和阀芯尾角为定值时,入口角增大,总熵产值减小;入口角和阀瓣宽为定值时,阀芯尾角增大,总熵产值增大。总体上,阀芯尾角相对于阀瓣宽和入口角对整体总熵产值的影响更为显著。

图5 入口角-阀瓣宽响应面Fig.5 Response surface diagram of the effect of inlet angle and valve flap width

图6 入口角-阀芯尾角响应面图Fig.6 Response surface diagram of the effect of inlet angle and spool tail angle

图7 阀瓣宽-阀芯尾角响应面Fig.7 Response surface diagram of the effect of valve flap width and spool tail angle
3.4 最优参数组合与分析
3.4.1 最优结构参数
采用统计学软件以最小总熵产为目标对响应面回归模型式(9)进行优化分析,得到预测理论最小总熵产值为269.53 mW/K。此时对应的结构参数为:入口角33.4°,阀瓣宽24.4 mm,阀芯尾角25.0°。根据以上结构参数建模并进行数值计算,得到直接耗散熵产为11.20 mW/K,湍流耗散熵产为259.32 mW/K,总熵产值为270.52 mW/K。预测值和计算值的误差小于0.4%,说明回归模型预测准确且优化结果可靠。而优化前轴流式止回阀的直接耗散熵产为11.85 mW/K,湍流耗散熵产为1 947.14 mW/K,总熵产值为1 958.99 mW/K,通过对比可知优化效果明显。
3.4.2 流阻系数对比
流阻系数是衡量阀门性能好坏的重要指标之一。对优化前、后轴流式止回阀在不同入口速度下的流阻系数进行计算,得到的结果如图8 所示。优化前的平均流阻系数为3.98,优化后的平均流阻系数为0.77。可知本优化方法可行且优化效果明显。

图8 轴流式止回阀优化前后流阻系数Fig.8 Flow resistance coefficients of axial flow check valve before and after optimization
3.4.3 熵产和流场分析
轴流式止回阀优化前后的直接耗散熵产率分布、湍流耗散熵产率分布和速度矢量分别如图9~11 所示。由图9、图10 以及第3.4.1 节可知,在能量损失组成方面,优化前后湍流耗散熵产占总熵产的95%以上,而直接耗散熵产只占小部分,且优化前后湍流耗散熵产变化较大,直接耗散熵产大小基本不变。在能量损失分布方面,优化前阀瓣区域(图中虚线左边)的直接耗散熵产和湍流耗散熵产主要分布在喉口后端,优化前导流罩区域(图中虚线右边)的直接耗散熵产和湍流耗散熵产主要分布在导流罩与阀瓣交接处附近。因为这两处曲率变化大,流体在这两区域发生分离,故存在较大熵产分布。而优化后轴流式止回阀的喉口结构前后圆滑过渡,阀瓣和导流罩自然贴合,阀瓣区域和导流罩区域内的直接耗散熵产和湍流耗散熵产分布明显减少。

图9 轴流式止回阀优化前后直接耗散熵产率云图Fig.9 Contours of entropy production rate of axial flow check valve by direct dissipation before and after optimization

图10 轴流式止回阀优化前后湍流耗散熵产率云图Fig.10 Contours of entropy production rate of axial flow check valve by turbulent dissipation before and after optimization
由图11 可以看出阀门内部流体的流动状况。原轴流式止回阀喉口后端、阀瓣边缘处和尾部发生了流动分离,形成了漩涡,且阀瓣边缘处速度梯度大,易造成较大流动损失;而优化后的轴流式止回阀漩涡明显减少,导流体上流动分离点明显后移,能量损失也随之减少,与熵产分析结果相符。
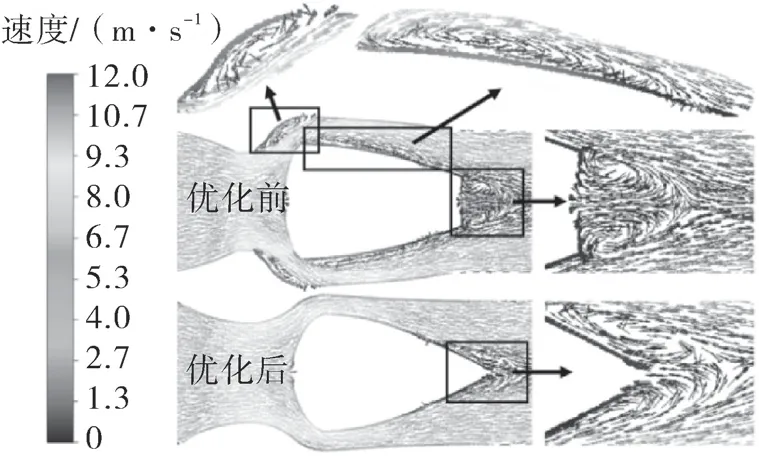
图11 轴流式止回阀优化前后速度矢量云图Fig.11 Contours of speed vector of axial flow check valve before and after optimization
4 结论
(1)运用熵产理论和响应面法对DN100 轴流式止回阀结构进行了优化设计。该止回阀最优结构参数入口角为33.4°,阀瓣宽为24.4 mm,阀芯尾角为25.0°,预测理论最小总熵产值为269.53 mW/K,与计算值270.52 mW/K 相差甚小,均远低于未优化前总熵产1 958.99 mW/K,且优化后平均流阻系数明显小于优化前平均流阻系数。可知优化方法切实可行且优化效果可观。
(2)湍流耗散熵产占轴流式止回阀总熵产的95%以上,优化后其数值和范围明显缩小,而直接耗散熵产只占总熵产小部分,优化后数值基本不变,范围明显缩小,两者主要发生在喉口后端和阀瓣边缘附近。优化前阀门喉口后端、阀瓣边缘处和导流罩尾部发生流动分离,形成了漩涡,优化后阀门内部漩涡明显减少,导流体上分离点明显后移,流通性能更好。进一步说明优化效果显著。

