市场经济下梯级水电站联合调度效益分摊方法

蒋谋智，程 雄，，李咸善，李英海，钟 浩

（1. 三峡大学水利与环境学院，湖北 宜昌 443000； 2. 梯级水电及新能源运行与控制湖北省重点实验室（三峡大学），湖北 宜昌 443002）

0 引 言

梯级水电站群联合调度能够利用不同库容补偿实现流域水资源高效利用［1，2］，但在市场环境下，由于各梯级水库调节性能和利益主体不同，在制定发电计划和报价策略方面基本上“互不沟通、各自为政”，这种模式虽然能充分发挥市场主体自由竞争优势，却非常不利于水资源高效利用，经常出现难以协调的矛盾：上游电站获得较多但下游电站获得较少的市场化电量，导致下游电站因来水过多面临严重的弃水风险；或者上游电站获得较少但下游电站获得较多的市场化电量，导致下游电站因来水不足面临“被迫降低水位”的不经济运行方式，甚至可能无水发电的严重后果［3，4］。合作博弈是国际上公认能破解该难题的有效途径［5］，但隶属于不同业主的梯级水电站群要维持联盟的稳定性和持续性，首要关键是如何解决联盟内多利益主体间公平分摊补偿效益问题［6］。

目前，国内外学者对梯级水电站补偿效益分摊问题做了许多研究，突出表现在：①按电站特性参数进行分摊，如单指标法［7］、综合分析法（模糊综合评判法［8］、离差平方法［9］等）分摊方式。按电站特性参数分摊操作简单，但是结果比较片面，难以体现公平性。②按电站在梯级效益增长中的贡献度进行分摊，分为单客观权重法和多个客观权重组合法，单客观权重法如夏普利（Shapley）值法［10］、逼近理想解（TOPSIS）法［11］等，多个客观权重组合法如变异系数-Shapley 值法［12］、Critic-Shapley 值法［13］等。单客观权重法的优点是能够公平的考虑效益边际贡献值，却忽略了个体偏好和特征；多个客观权重组合方法能够充分考虑效益贡献度与电站客观参数对分配结果的影响，分配结果各方更易于接受。然而，Shapley 值法需要遍历所有子联盟组合，随着主体数量的增加，Shapley 值法计算量会呈指数级增长，求解难度大大增加。此外，水电现阶段已经深度参与电力市场竞争，市场需求对于电价影响很大，在电站调度的过程中需要考虑市场化对电站效益的影响［14］，目前电力市场环境下效益分摊主要考虑丰枯电价对效益的影响［10］和水电消纳问题［15］，对于完全市场化的水电电价及较多主体联盟效益分摊情况考虑较少。

本文以乌江流域梯级电站为背景，提出市场经济下梯级水电站群联合调度效益分摊方法。该方法首先以市场经济下的发电效益最大模型对不同梯级水电站联盟进行联合调度；然后利用竞争力指数法将电站特征参数转化为电站竞争力代表的效益分摊比例，用信息熵法将市场经济下电站间复杂效益联系量化为各电站贡献度代表的效益分摊比例，用线性加权将两方法结合，以解决市场经济下多主体电站联盟效益分摊问题；最后采用满意度评价与分配策略倾向分析（modified disruption propensity，MDP）对分摊结果进行双重评定，来判断分摊方法的公平性与合理性。实例结果表明，本文方法能有效解决市场经济下多主体梯级水电站群效益分摊问题，对实现市场背景下的梯级水电联合优化调度具有一定参考意义。

1 数学模型

1.1 目标函数

发电效益最大模型是评估市场经济下梯级水电站群优化调度最常用模型，但若只考虑发电收益不考虑供电可靠率，在遭遇极端干旱天气时，梯级水电站群发电困难容易影响电网安全稳定，因此，本文构建了考虑保证出力限制的发电效益最大模型，目标函数如下式：

式中：FN为目标值；N为联盟电站数量；t为时段序号；T为时段总数；Nti为第i座电站在t时段的平均出力，MW；Δt为t时段小时数，h；ptN为N座电站联盟时第t时段上网电价，元/kWh；α为惩罚系数；为第i座电站在t时段保证出力，MW。

1.2 约束条件

（1）水量平衡约束。

式中：Vit，Vit+1表示电站i在第t时段始末库容，m3；Qti，input和Qti，output为电站i第t时段的入库流量和出库流量，m3/s。

（2）电价约束。

式中：pt，maxN、pt，minN表示N座电站联盟时第t时段平均电价上下限，元/kWh。

其他约束包括库容约束、出力约束、出库流量约束等。

2 模型求解

本文模型求解主要分两步：首先是求解不同梯级联盟的总发电效益，涉及的关键子问题是如何确定子联盟的入库流量以及如何拟合电量与电价关系；其次是对联盟效益进行公平分摊，涉及的关键子问题是如何公平分摊补偿调度效益以及如何评价分摊方案的优劣，下面分别针对这些子问题进行介绍。

2.1 确定子联盟的入库流量

梯级电站完全联盟与单独调度情形下各电站入库流量为上游电站出库流量与自身区间流量之和；梯级电站不完全联盟时，子联盟内除龙头电站外的下游电站入库流量计算与完全联合调度时一致，子联盟的龙头电站i入库流量计算公式如下：

式中：Qti，input表示子联盟龙头电站i的入库流量，m3/s；

表示子联盟龙头电站

i

的

k

座上游电站在第

t

时段区间流量之和，m

3

/s。

2.2 拟合电量与电价关系

水电市场化后，由于联盟调度可以充分利用补偿库容，获得更强市场竞争力，梯级电站会更倾向于以梯级联盟的形式参与市场竞争。联合调度时为维持联盟内部稳定性，同一个联盟采用相同电价，而不同联盟由于发电能力与运维成本导致的市场议价能力差异，使得各联盟在市场中成交的电价不同，即形成“一个联盟一个电价”的市场电价模式。

本文假定所有电站均参与中长期双边交易市场且发电量都能成交，根据市场规律，市场电价呈现出随市场电量增加而降低的趋势，此现象通常采用价格需求函数来描述［16］，即：

式中：Nti，max表示第i个电站在t时段的最大出力，MW；表示N座电站联盟时第t时段最大发电量，亿kWh。

2.3 补偿效益分摊方法

补偿效益是指梯级电站联合调度效益减去单站调度总效益后剩余效益，公式如下：

式中：ΔB表示补偿效益；BN表示N座电站联合调度时总效益；B（i）表示第i座电站单独调度时效益，单独调度时各电站电价单独计算，计算方式同式（6），联盟电站数取1。

补偿效益分摊是梯级联盟剩余效益再分配过程，是保障联盟稳定的核心环节。一般来说，效益分摊应遵循公平、合理、高效三原则，目前应用最广泛的Shapley值及其客观权重组合法在进行N座电站联盟补偿效益分摊计算时，所需效益信息量为2N-1 条，当主体数量大于5 时，Shapley 值法便不再适用［17］。为此，本文提出一种信息熵-竞争力指数组合法进行补偿效益分摊。该方法首先通过信息熵法量化梯级联盟调度中各电站对补偿效益的贡献度，然后利用竞争力指数法计算各电站在联盟内部竞争力，以线性加权法将两者结合得到补偿效益的分摊比例，具体求解思路如下。

2.3.1 信息熵值法求解思路

文献［18］提出了一种基于信息熵的补偿效益分配方法，应用于N人合作博弈问题的求解中，这种方法可以用较少的信息得到合理且稳定的分配结果，其基本思路如下：

（1）求解各电站效益分配下限：

式中：B(N1)、B(Ni)、B(NN)分别表示除去第1、第i、第N座电站的（N-1）座电站子联盟的效益；分别表示第1、第i、第N座电站效益分配下限。

（2）计算结余效益RN：

（3）计算结余效益分配比例：

式中：px，i表示第i座电站结余效益RN的分配比例，也表示信息传递载体，-px，ilnpx，i表示px，i的平均信息量，px，i表示传递px，i所需要的平均数据值，式（10）表示信息熵最大值在所有px，i的单位数据信息量最大时取得。

（4）计算电站分配效益：

式中：Si为第i座电站以信息熵法确定的分配效益。

（5）结合式（7），计算电站补偿效益分配比例：

式中：PPX，i为第i座电站以信息熵法确定的补偿效益分配比例；其他符号见式（7）和式（11）。

2.3.2 竞争力指数法求解思路

竞争力指数法是利用因子分析法对多主体多重特征参数进行参数系数赋权，将特征参数转化为主体竞争力数值，计算简便、直观，便于使用。梯级电站特征参数种类较多，且电站间存在很强的竞争合作关系，根据因子分析法的基本思想，可将联盟内各电站特征参数量化为电站竞争力，以某电站竞争力在联盟竞争力中所占比重作为该电站补偿效益分摊的比例依据。设梯级有N个水电站，J类个体特征参数参与计算，电站参数矩阵记为X=（xij）N✕J，竞争力指数法计算电站补偿效益分配比例步骤如下：

（1）对电站参数矩阵（xij）N✕J进行巴特利特（Bartlett’s）形检验与抽样适合性（Kaiser-Meyer-Olkin，KMO）统计值检验，若球形检验值小于0.05、KMO 统计值大于0.5，说明电站参数间具有良好相关性，适合进行因子分析。

（2）对电站参数进行主成分分析，采用最大方差法旋转进行参数主成分测算，得到解释电站参数的总方差解释表、M个主成分和主成分矩阵A=（ajm）J✕M。

（3）计算电站主成分参数线性化组合中的系数：

式中：λm为第m个主成分参数特征根；ωjm为电站第j个参数在第m个主成分参数线性化组合中的系数。ajm表示第j类参数在第m个主成分矩阵的值。

（4）计算电站参数系数权重：

式中：Em表示第m个主成分方差；M表示主成分数目；μj表示电站第j类参数系数权重。

（5）对电站参数系数进行归一化处理：

式中：υj表示电站第j类参数系数归一化后值；J表示参与计算特征参数种类数目。

（6）计算电站竞争力指数值：

式中：Zi表示第i座电站竞争力指数，xij表示第i座电站第j类参数值。

（7）计算电站补偿效益分配比例：

式中：PPC，i表示第i座电站以竞争力指数法确定的补偿效益分配比例。

选取装机容量、保证出力、多年平均发电量、调节库容、额定水头五项特征参数作为电站竞争力计算指标，其分别表示梯级电站最大出力、电站有保证的发电出力、电站多年平均发电能力、电站调蓄能力、电站经济技术水平。

2.3.3 信息熵-竞争力指数组合法

信息熵法可以较好量化梯级电站的补偿效益贡献关系，但是无法考虑电站自身特征参数对效益分摊的影响；竞争力指数法可以将各电站特征参数量化为联盟内部竞争力，但是完全从电站特征参数出发，没有考虑梯级电站间效益的关联性。采用线性加权法将信息熵与竞争力指数法结合可有效弥补上述方法不足，同时在一定程度上克服乘法合成归一化方法带来的权重倍增效果［19］。N座电站联盟补偿效益分摊时，由竞争力指数法确定各电站补偿效益分配比例PPC，i，由信息熵法确定各电站补偿效益分配比例PPX，i，根据加法集成原理确定出最终的组合分配比例，计算公式如下：

式中：Pfinal，i表示第i个电站最终的组合分配比例；φ和β分别表示两方法占组合权重的比例系数。

利用差异系数法对φ求解，计算公式如下：

式中：ψ1，ψ2，…，ψN为升序排序后的PPC，i。

结合式（7），第i个电站按信息熵-竞争力指数组合法（简称信-竞法）最终分配效益为：

式中：Xi表示电站i参与联合调度时的最终效益分配值；其他符号参见式（7）和式（18）。

信-竞法进行N座电站联盟补偿效益分摊时仅需N+1 条信息量：N座电站联盟与任意（N-1）座电站子联盟的效益信息，因此该方法可以用于较多电站主体效益分摊的情形。

2.4 分摊结果评价方法

2.4.1 评价方法1：满意度评价

对于多利益主体梯级电站而言，协商补偿效益的分配方案等价于各电站主体针对补偿效益合作博弈模型的解，合作博弈模型的解以所有主体对分配方案的满意度尽量均衡为目标。本文满意度为各主体按不同分配方法分配的补偿效益与理论补偿效益之比，主体满意度越高，越倾向于留在联盟内，各主体满意度越接近，联盟越稳定，计算公式如下：

式中：C表示满意度值；δi表示第i座电站的理论补偿效益，为电站i理论上可以获得的最大补偿效益；其他符号见式（7）和式（8）。

2.4.2 评价方法2：分配策略倾向分析

分配策略倾向分析（MDP）是对分裂倾向（propensity to disrupt ，PTD）进行修正后的指标［20］，用于合作博弈主体策略选择分析，MDP 能明确给出主体联盟意向门槛值，物理意义更为直观。N座电站联合调度效益分摊时i电站MDP 值计算公式如下：

式中：Xf表示除去i电站的第f座电站最终效益分配值；表示电站i参与合作时除去i电站后其他（N-1）座电站获得的总收益分配值；Di代表电站对合作博弈分配策略的倾向值，若Di1，则参与者i拒绝该分配策略；若0＜Di＜1，参与者i接受该分配策略。

3 实例分析

3.1 工程背景及案例设计

以乌江流域梯级水电站群洪家渡、东风、索风营、乌江渡、构皮滩、思林六座电站为研究对象，对本文模型及分摊方法进行验证。电站基本资料及其拓扑结构见图1，市场电价上下限参考实际电价设为0.2～0.4 元/kWh。

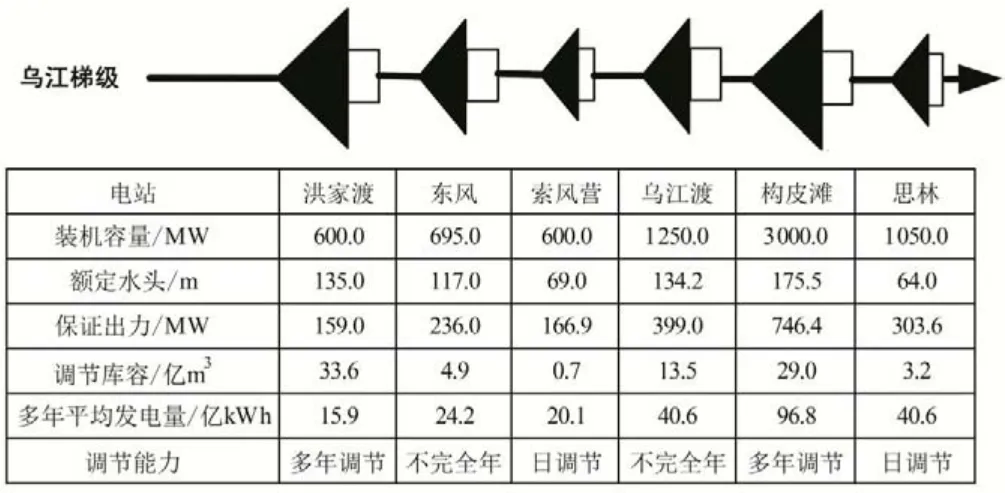
图1 乌江梯级电站拓扑图Fig.1 Topology diagram of Wujiang cascade hydropower stations

首先对六座电站进行竞争力指数分析，目的是得到联盟电站内部竞争力，作为代表电站特征的补偿效益分摊依据。在此基础上，设计了两组案例，案例1 以洪家渡为龙头电站，下游随机选取两座不同调节能力的电站组成合作联盟，采用平水年实际月平均流量进行梯级优化调度，以不同方法进行补偿效益分摊，对分摊结果进行满意度与MDP 评价，目的是比较市场经济下不同效益分摊方法优劣，验证本文方法的合理性与公平性；案例2选取梯级六座电站以平水年实际月平均流量进行联合调度，进一步验证本文方法能否高效求解市场经济下数量较多的梯级水电站群效益分摊问题。

3.2 梯级六电站竞争力指数分析

为确定六座电站联盟情形下补偿效益分摊比例，需对六电站特征参数进行竞争力指数分析，分析结果也可作为其中部分电站联盟时补偿效益分摊依据。对梯级六座电站五类特征参数进行因子分析计算后结果如表1和表2，从表1中可以看出电站特征参数累计解释值为96.859%，说明提取的主成分总方差对参数总方差的贡献率高，解释效果好。五类特征参数的Bartlett’s 球形检验值为0.01、KMO 统计值检验为0.61，电站参数适用于因子分析。

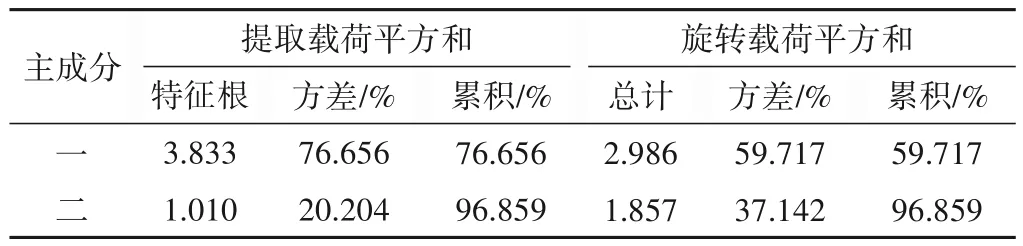
表1 电站参数总方差解释表Tab.1 Explanation table of total variance of hydropower station parameters

表2 参数主成分矩阵及电站参数系数计算结果Tab.2 Results of parameter principal component matrix and parameter coefficient of power station

从表2 左侧主成分矩阵中可以看出：第一类主成分三类参数矩阵值均大于0.9，第二类主成分中两参数矩阵值分别为0.723与0.460，虽第二类主成分中两参数相关性相对较弱，但由于装机容量等三类参数在第二类主成分中矩阵值均为负数，没有相关性，因此五类参数分为两类主成分是合理的。如表2 右侧所示：对电站参数系数计算得到各类参数系数权重进行归一化处理，结合各电站参数值在联盟中占比情况转化为六电站竞争力指数值如下：构皮滩、洪家渡、思林、东风、索风营竞争力指数值分别为0.35、0.18、0.17、0.12、0.11、0.07。电站竞争力指数值越大，说明电站在联盟内竞争力越强，效益分摊时应考虑各电站竞争力不同导致的补偿效益诉求差异问题，以保证联盟的稳定性。

3.3 案例1：洪家渡与其他两座电站联盟效益分摊

为验证本文分摊方法在市场经济下效益分摊的合理性与公平性，将不同联盟（洪东构、洪东索、洪索构、洪索思）联合调度所产生的补偿效益用信-竞法、变异系数-Shapley 值法［12］和Critic-Shapley 值法［13］3 个方法进行分摊，采用满意度和MDP 值对分摊结果进行双重定量评价，分析不同分摊方法在市场经济下的适用性。不同分摊结果如表3、4 与图2 所示，图2 中方法1、2、3 分别表示信-竞法、变异系数-Shapley 值法和Critic-Shapley值法。

表3 各电站不同补偿效益分摊方法结果Tab.3 Results of different compensation benefit allocation methods for each hydropower station

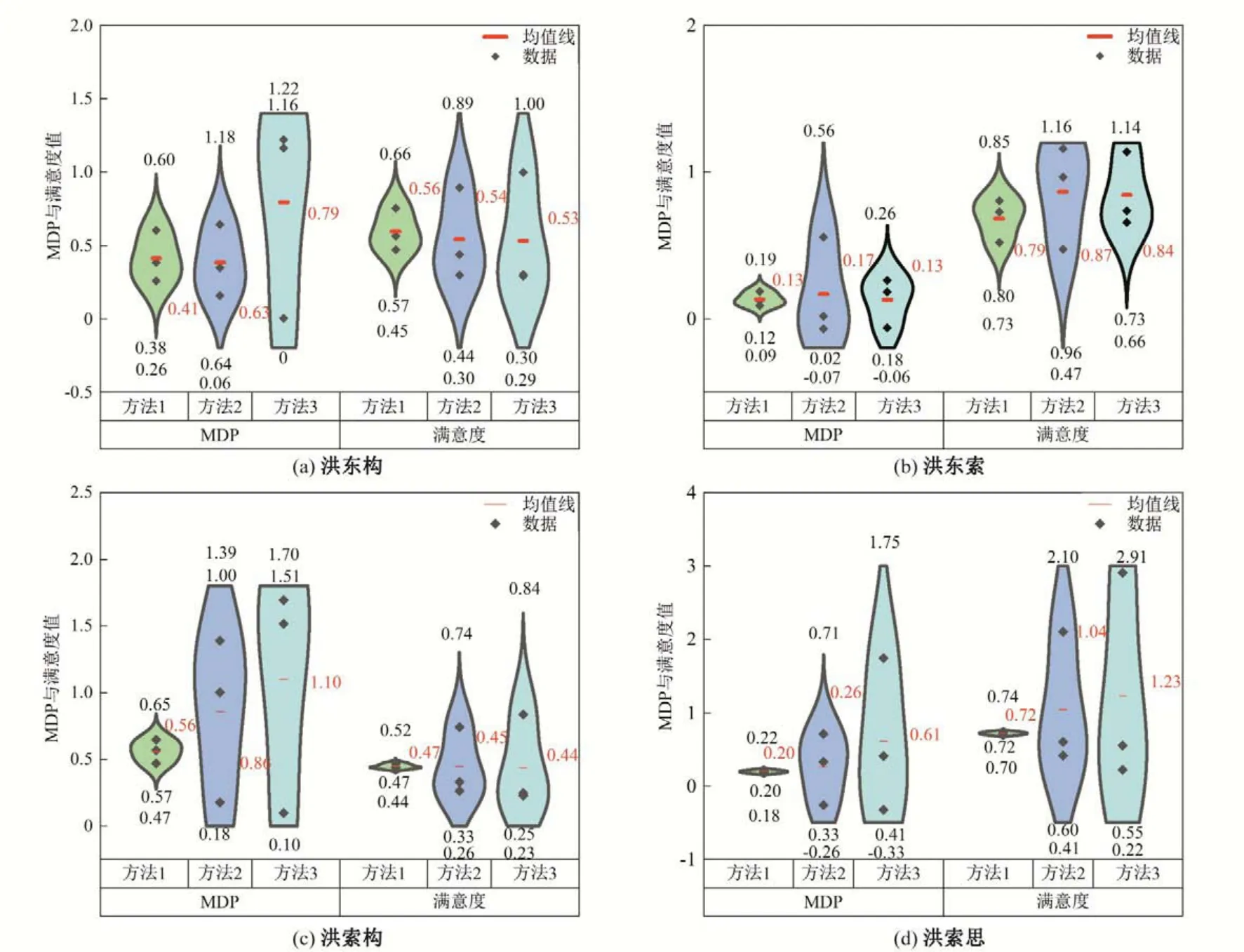
图2 不同方法下各联盟中主体MDP与满意度Fig.2 Subject MDP and satisfaction in different alliances under different methods

（1）首先分析市场经济下各方法合理性问题。3 种方法各电站在联合调度中分得效益大于单独调度，都具有一定合理性。从表3 中可以看出：信-竞法与变异系数-Shapley 值法分配结果较为相近，与Critic-Shapley 值法分摊结果相差较大。以洪东索联盟为例，信-竞法分摊比例为0.39、0.41、0.20，变异系数-Shapley 值法分配比例为0.44、0.27、0.29，Critic-Shapley 法分配比例为0.30、0.41、0.28，可以看出信-竞法和变异系数-Shapley值法都给予龙头电站较大权重，但是Critic-Shapley 值法较少考虑东风电站贡献，而Critic-Shapley 值法分摊时洪家渡比例仅为0.3，效益增长仅为0.4 亿元，低于其他两座电站，较为不合理。从洪东构、洪东索、洪索构、洪索思四联盟中各电站分配比例来看，信-竞法分摊结果更为合理。

（2）然后分析市场经济下各方法分摊结果公平性问题。从MDP 值和满意度综合来看，4 种联盟情形下，信-竞法在各联盟中电站主体效益分配业主满意度最接近的同时MDP值最小，为最公平分配方案。① 从图2 和表4 中4 种联盟情形下不同分摊方案的MDP 值及均方差平均值来看，3种方法MDP 最大值分别为0.65、1.39、1.75，方差平均值为0.07、0.41、0.57。信-竞法分摊时MDP 均值分别为0.41、0.13、0.56、0.20，均方差分别为0.14、0.04、0.07、0.02；变异系数-Shapley值法分摊时MDP均值分别为0.63、0.17、0.86、0.26，均方差分别为0.46、0.28、0.51、0.40；Critic-Shapley 法分摊时MDP 均值分别为0.79、0.13、1.1、0.61，均方差分别为0.56、0.14、0.71、0.86。从MDP 值的均方差和最大值综合来看，信-竞法分摊结果MDP 值方差最小，结果最好，为最优分配方案，变异系数-Shapley值法其次，Critic-Shapley 值法最差，且后两种方法分摊时MDP 值均有大于1 或小于0 的情况，梯级电站联盟倾向于分裂。② 从分摊结果满意度值来看，四种联盟情况下三种方法的满意度值均值分别为0.64、0.72、0.76，满意度均值较为接近，满意度均方差平均值分别为0.05、0.38、0.51，信-竞法分摊结果各主体满意度均方差最小，联盟最稳定。

表4 不同方法下各主体MDP与满意度均方差平均值Tab.4 Mean value of MDP and satisfaction degree of each power station under different methods

（3）从三方法的公平性和合理性评价来看，Shapley 值法及其组合法在市场经济下的补偿效益分摊应用存在一定局限性。主要原因是当电站以联盟的形式参与市场竞争后，梯级调度模式与传统模式存在较大区别：①如图3所示：市场经济下梯级联盟会通过将汛期的水能转移到枯期实现梯级效益增长，因为电价在枯期相对较高；②Shapley值法认为任意电站子联盟出现的概率都是相等的，但在市场经济下梯级电站会倾向于与调节能力强的电站结盟，导致某些子联盟情形出现概率较低，使得Shapley 值法计算效益贡献时出现偏差；③ Shapley 值及其客观权重组合法进行3 座电站效益分摊时需要计算的效益情况为23-1=7 种，而信-竞法仅需3+1=4 种；信-竞法以更少的计算信息量取得更好的分配结果。

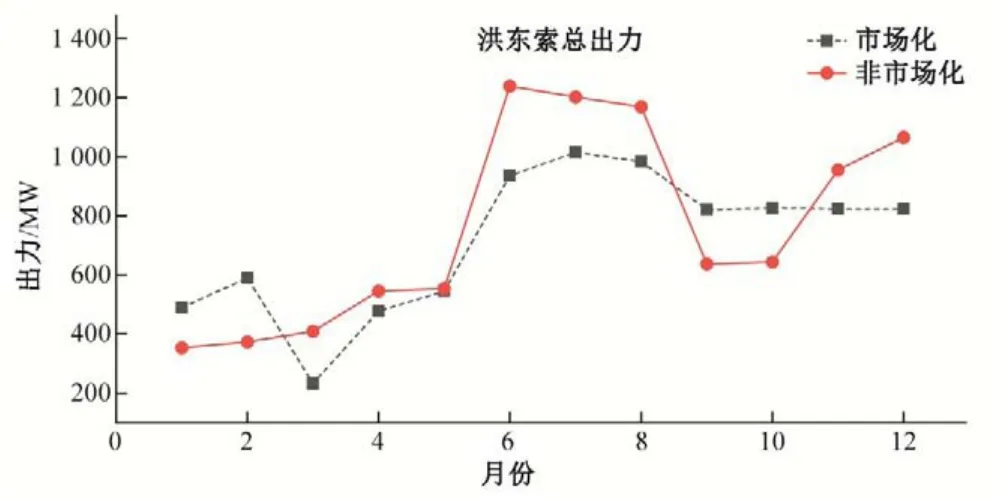
图3 调度结果对比Fig.3 Comparison of scheduling results

3.4 案例2：梯级六库效益分摊

为进一步探究信-竞法在数量更多梯级水电站群效益分摊情况，本节以乌江梯级六座电站作为研究对象。假设六座电站分属于不同业主，当进行补偿效益分摊时，联盟内各电站可能会更关注效益的损失，为了对比分析信-竞法的公平性与合理性，引入损失比例法：以联盟中失去i电站造成的效益损失为分摊依据。对联合调度补偿效益采用信-竞法与损失比例法进行分摊及结果评价，调度结果如表5所示。

表5 各电站不同联盟情形下调度结果亿元Tab.5 Dispatching results of each power station in different alliances

由表5中分析可知：①除龙头电站外，具有较好调节能力的中游电站参与合作联盟可显著增加梯级补偿效益。如表5 所示：六座电站联盟调度时梯级补偿效益为6.4 亿元；构皮滩不参与联盟时，梯级产生的补偿效益最少，仅为3.8 亿元，当东风或索风营不参与联合调度时，补偿效益分别为5.3 亿元与5.6 亿元，东风与索风营对于梯级补偿效益贡献较低，说明具有较好调节能力的中游电站在梯级水电站的优化调度中可以提高梯级补偿效益，与文献［10］得出结论相印证，因此在效益分摊中要考虑调节能力较好的中游电站为联盟做出的贡献。②市场经济下，信-竞法可以在电站数量较多的合作联盟中以较少的计算量取得公平合理的补偿效益分配结果，同时对调节能力较强中游电站进行了合理补偿。六电站联盟效益分摊结果及评价结果如表6所示。

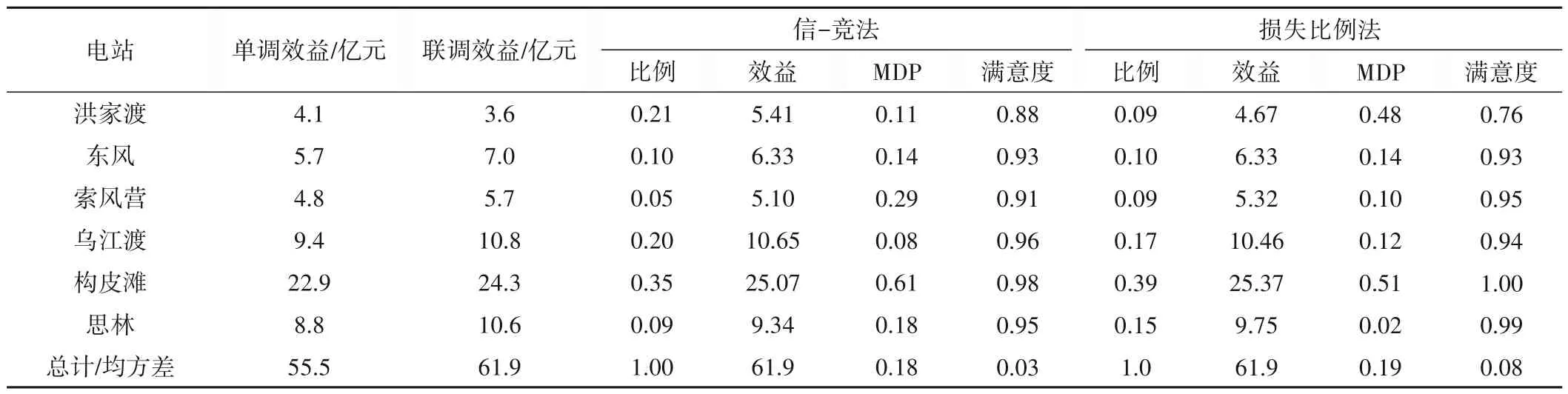
表6 各电站增益分配结果MDP与满意度Tab.6 MDP and satisfaction degree of gain distribution results of each hydropower station

由表6分析可知：采用信-竞法与损失比例法进行效益分摊后，各电站效益相对单独调度都有增长，分摊结果都具有一定合理性。信-竞法分摊时，洪家渡与构皮滩分别分得补偿效益1.1 亿元、1.7 亿元，占梯级补偿效益的44%，联盟中构皮滩MDP值最大为0.61，原因是该电站盈利能力较强，效益基数高，因此在分得补偿效益26%的情况下，其MDP 依然较高，但是小于1，说明该电站依然倾向于留在联盟内，六座电站满意度值均在0.9左右，均方差为0.03，MDP值均方差为0.18；损失比例法分摊结果MDP 最大值为构皮滩0.51，其次为洪家渡0.48，MDP 值均方差为0.19，六电站满意度最低为0.76，最大为1，均方差为0.08。从两方法龙头电站分摊比例来看，信-竞法为0.21，损失比例法仅为0.09，损失比例法没有考虑龙头电站对梯级的补偿调度贡献，信-竞法更为合理；从两方法MDP值与满意度值及两方法均方差综合来看：信-竞法分摊结果更为公平。六座电站分摊结果说明，在多主体联合调度情形下，信-法可以用较少信息公平有效的解决梯级电站合作联盟效益分摊问题。该方法的优点是：用较少的计算量较好地反映了梯级电站合作博弈的补偿关系及梯级联盟内部的竞争情况，量化了个体在补偿效益产生中的作用大小及竞争强度，使梯级各电站倾向于留在联盟中，梯级合作联盟长久进行。6座电站效益分摊信-竞法仅需6+1=7 条效益信息，而Shapley 值及其客观权重组合法则需要26-1=63条效益信息，信-竞法在结果公平合理的前提下大大降低了计算量，更具有优势。

4 结 论

本文针对市场经济下多主体水梯级电站联合调度补偿效益分摊问题，将信息熵法与竞争力指数法相结合，提出信息熵-竞争力指数法，并将其应用于乌江流域梯级中3 座与6 座水电站联合调度效益分摊实例中，同时与其他分摊方法进行对比，采用满意度评价与分配策略倾向分析对各方法分摊结果进行双重评定。本文得出的主要结论如下：

（1）市场条件下，梯级水电经过合作博弈联盟产生的效益大于作为独立个体参与电力市场的效益，梯级水电会更倾向于以合作联盟的形式参与电力市场。

（2）信息熵结合竞争力指数法可有效解市场经济下联盟电站数目较多时的补偿效益分摊问题，用较少的计算量得到公平合理的效益分摊结果，相较于以Shapley值法为基础的客观权重组合分摊方法，信息熵-竞争力指数法在公平性和计算量上具有明显优势。

（3）在进行梯级联盟调度的过程中，各电站需要兼顾生态用水及生产生活的需要，目前梯级电站效益分摊计算，对这些社会贡献及生态贡献方面考虑较少，如何量化梯级电站的社会贡献及生态贡献，需要进一步研究。