基于自适应MOEA/D 的供水管网多目标优化

董 娜

（内蒙古电子信息职业技术学院电子与自动化学院，内蒙古 呼和浩特 010070）

0 引 言

城市供水系统是整座城市的生命线，完善的供水管网能够保障人民群众日常生活的正常运转。在城市供水系统中，管网优化设计一直是研究热点问题之一［1］。在管网设计时，要求在满足供水需求量和水压等约束条件下，期望能尽量减少节点富余水头总和，以降低管网设计的故障率，增强其可靠性。同时，又期望尽可能降低管网建造总成本，以提高管网建造的经济性。显然，总造价和故障率是一对具有冲突特性的目标函数。随着总造价的提高，故障率呈下降趋势；反之，随着总造价的降低，故障率呈上升趋势。因此，供水管网设计显然是一个多目标优化问题［2］。传统的单目标优化方法需要利用权重系数将多目标优化问题转化为单目标优化问题。但是权重系数极难确定，而且对算法结果影响巨大。由于多目标进化算法一次运行能够获取多个Pareto最优解，适合于解决管网多目标优化问题。研究者将其应用在城市管网优化设计当中，为市政工程的施工建设提供有益参考［3，4］。

基于分解的多目标进化算法（MOEA/D）采用分解方法将一个多目标优化问题转化为一组单目标优化子问题，并以协作的方式处理它们。MOEA/D公认为是多目标进化领域的主流算法之一［5］。MOEA/D 在实际工程领域具有广泛的应用，如无人机航迹规划［6］、能源计划优化［7］、网络接入控制［8］、楼宇负荷优化［9］、天线优化［10］、飞行器气动外形优化［11］等。MOEA/D在解决一些复杂多目标优化问题时，其难以发现目标空间中Pareto 前沿上的边界解，而与这些边界解对应的决策空间中的输入矢量有可能是期望的Pareto最优解［12］。

为了取得收敛性和多样性的最佳平衡，研究者提出多种改进方法。例如：LI 等人将差分进化算子（DE）引入到MOEA/D中，形成MOEA/D-DE 算法［13］。ZHANG 等人设计一种基于精英群体的自适应权重向量调整策略，并集成到MOEA/D 中形成MOEA/D-AWA 算法。MOEA/D-AWA 通过引入精英群体，以在目标空间稀疏区域添加新的子问题，从而能够有效解决复杂MOP问题［14］。LI等人设计一种自适应交配选择策略，提出一种简单有效的稳定匹配模型来协调选择过程［15］。此外，如自适应交配选择机制、邻域大小集合、可变邻域策略等均已成功集成到MOEA/D中来解决实际工程问题。

然而，实际工程中大多数多目标优化问题具有复杂的Pareto 最优前沿，比如长尾巴、尖峰或不连续。以供水管网优化问题来说，总造价和故障率不一定呈现出标准的Pareto 前沿。我们总是期望，当总造价缓慢增加时，故障率将会缓慢降低；当总造价缓慢降低时，故障率将会缓慢增加。然而，现实情况却是，在某个临界点后，总造价的些许降低可能导致故障率的极大增加，总造价的极大增加也可能无法使故障率有些许降低。这就出现了所谓的长尾巴、尖峰等复杂Pareto 前沿的情况。针对这些复杂优化问题，其中一个目标的细微变换会导致另一个目标较大的变换，从而导致Pareto 最优解集中在Pareto 前沿的中部区域，边界区域很难获取到Pareto 最优解。显然，传统MOEA/D难以有效完成这类问题的寻优。

主要针对供水管网多目标优化呈现的Pareto解集前沿面存在尖峰、长尾和不连续等问题，提出一种带有两阶段策略和小生境引导策略的MOEA/D 算法（MOEA/D-TPN），旨在解决Pareto 解的多样性和分布性的不平衡问题。然后利用MOEA/DTPN 算法求解城市供水管网多目标优化问题，获取双环管网的最优解集，为城市供水管网的工程设计提供可行参考方案。

1 城市供水管网多目标优化问题

管网形式主要分环状和树状，树状主要用于边缘地区，其他地区一般布置环状管网以保证用水安全。Alperovits 与Shamir 提出的双环管网是公认的管网优化模型，如图1 所示。它包含了1个水源、7个节点和8个段长1 000 m 的管段，海曾威廉系数设定为130［16］。表1 给出了各节点的节点高程、最低自由水头和需水量等参数。

图1 双环管网结构图Fig.1 Structure diagram of double ring pipe network

根据双环管网和单元管段的结构，可得到如下的供水管网经济性目标函数，即管网的总造价［16］：

式中：P为管网每年大修与折旧的费用在整个管网造价中的比例；E=［j（1+j）n］/［（1+j）n-1］为基建投资效果系数；j为银行利率；n为资金回收期；np为管网的管段数；Di、li分别为第i段管道的直径和长度；a+bDiλ为管网建造费用，a、b和λ分别为管道造价公式的系数及指数；H0为水泵静扬程；hi为管段i的水头损失；Qp为进入管网的总流量，K=（24×356×10 000γσ）/（102η）=8 600γ σ/η；σ为泵站电价；γ为管网使用年限内管网供水不均匀所占比；η为泵站效率。

由于节点富余水头越大，管网中水压越高，事故发生的概率就越大，因此可靠性目标函数定义为节点富余水头总和，即管网的故障率［16］：

式中：Hi为节点i处的自由水头：Himin为节点i处要求的最小水压；I为管网节点总数；Hi-Himin为节点i的富余水头。

2 MOEA/D原理

MOEA/D利用分解方法将多目标优化问题转换为一系列单目标优化子问题，并构造问题导向的邻域关系，然后以协同方式同时处理所有子问题，最终得到完整的Pareto 前沿［5］。常用的分解方法有权重聚合法、切比雪夫法和基于惩罚的边界交叉法［5］。由于权重聚合法不能很好地处理真实Pareto 前沿为凹状的问题，基于惩罚的边界交叉法的性能受惩罚因子的影响较大，因此以切比雪夫法为例进行研究。在该方法中，第i个子问题定义为如下形式：

其中，z*=min｛fi（x）|x∈Ω｝，i=1，2，…，m，λ=（λ1，λ2，…，λm）T为权重向量，满足λi＞=0，且有

3 MOEA/D-TPN算法

考虑到公式（3）是z*作为参考点，当其处理复杂凸优化问题时，算法寻找到的Pareto 最优解会向Pareto 前沿中部区域聚集。对于该问题，如果采用znad作为参考点，算法将能够寻找到边界区域的Pareto解。上述思想如图2所示。

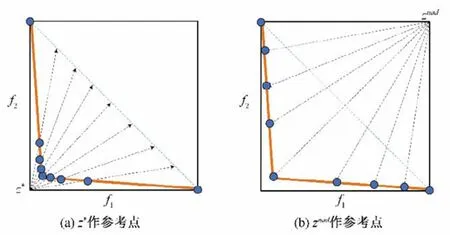
图2 Pareto解集分布情况Fig.2 The distribution of Pareto solution set.

基于此，提出一种自适应MOEA/D 算法，其将进化过程分成两个阶段。在第一阶段利用z*作为参考点，在第二阶段利用znad作为参考点。同时为了增加算法的多样性，设计了一套小生境引导策略，以选择不同的交配个体。

3.1 两阶段策略

第一阶段采用公式（3）将多目标优化问题分解成子问题进行协同优化。第二阶段采用公式（4）将凸多目标优化问题分解成子问题进行协调优化。

其中，znad=max｛fi（x）|x∈Ω｝，i=1，2，…，m。

然而，在处理多目标优化问题时，一般无法事先知道问题的凸凹性。因此何时选取公式（3）和公式（4）对问题进行求解存在困难。本文所提两阶段策略，在最大迭代步数的Mr%，使用公式（3）处理多目标优化问题。在第一阶段结束时，使用基于拥挤的方法来评估MOEA/D 是否得到了一组均匀解［12］。该方法能够估算出Pareto 前沿中间区域和极端区域的解的密度。如果中间区域的解比极端区域的解更密集，则说明多目标优化问题可能是凸的。基于此，在第二阶段，采用公式（4）处理多目标优化问题。

下面阐述基于拥挤的评估方法的原理［12］。由于在MOEA/D 权重向量λ满足λ1+λ2+ … +λm= 1，根据几何平均不等式定理，始终成立，因此λ位于超平面λ1+λ2+ … +λm= 1 的中心。换句话说，越大，权重向量就越接近中心权重向量。因此，将MOEA/D 的n个权重向量集分为两个子集，即中间子集Wm和极端子集We：

其中，Ωλ是MOEA/D 运用单纯形格子法生成的n个权重向量集。公式（5）中设置系数为0.5，能够取得Wm和We的最佳分类。

然后，根据权重向量子集Wm和We，将种群分为两个子种群，分别称为中间区域子种群Pm和极端区域子种群Pe。两个子种群的拥挤程度采用公式（7）和（8）进行估计：

式中：Dmid和Dext分别是中间子种群和极端子种群的拥挤度值；γ(i)表示子种群中第i个解的拥挤度，定义如下：

式中：d（i，j）为解i与j之间的距离；B（i）和T分别为解i邻域内的个体和邻域大小。

3.2 小生境引导策略

传统MOEA/D 在邻域交配和更新时会产生许多类似的解。尽管在MOEA/D-DE 中使用DE 算子取代了模拟二进制交叉算子，以克服该问题。但是当Pareto前沿具有不连续区域时，这种缺陷会导致种群多样性急剧降低。

参考文献［12］提出一种具有自适应选择能力的小生境引导策略。在该策略中，首先计算出每个个体在其相邻个体上的生态位计数。每个个体i的生态位计数是通过对相邻个体求和获得的一个共享函数，用nc（i）来表示：

式中：dij是个体i和j之间的距离；sh（dij）是测量个体i和j之间相似程度的共享函数，定义为：

式中：σshare是一个预先定义的生态位半径；α是一个常数，称为共享水平。

如果个体的生态位计数超过了给定的阈值，这意味着个体与它的邻接个体相似，所以最好选择邻域之外的个体作为交配的父代种群。因此，自适应更新定义如下：

其中，β是与生态位半径σshare密切相关的阈值，即β主要由σshare决定。由于nc（i）的最大值为T，将β设为T/2。P和P′产生方法如下：

其中，当rand1和rand2在范围［0，1］内独立生成随机数时，P与MOEA/D-DE 中的P保持相同。P′的定义意味着如果个体i的生态位计数达到阈值β，它有50%的机会选择其周围的个体作为交配父代种群。

3.3 MOEA/D-TPN算法框架

其中，是的第k个分量，xrk1、xrk2和xrk3是从种群中随机选择的3 个不同个体。CR和F是两个控制参数。采用多项式突变策略从产生一个解y=（y1，…，yn）：

其中，rand是［0，1］区间随机数，η和Pm分别是分布指数和突变率，bk和ak分别是决策变量的上下界。

4 实验分析

4.1 参数设置

MOEA/D-TPN 的参数设置如下：种群规模N=100，邻域规模T=20，nr=2，最大迭代次数maxIteration=100；从邻域内选取解的概率δ=0.9；差分进化的杂交率CR=0.5，尺度因子F=0.5；多项式变异的变异率pm=1/n，分布性指数η=20。

4.2 基准测试

为了评价MOEA/D-TPN 的有效性，采用6 个具有长尾巴、尖峰等复杂POF 的MOP （F1-F6）作为测试案例［12］，决策变量个数均设置为20，取值范围在［0，1］n，具体信息见表2。

表2 具有复杂POF的MOPTab.2 MOP with complex POF

4.4 实验结果

图3 给出了MOEA/D-TPN 的逼近结果，并与MOEA/D-DE和MOEA/D-STM 进行了对比分析。可以看出，对于F1 测试问题，MOEA/D-DE 和MOEA/D-STM 获取的解会收敛到POF 的中间区域，难以发现边界解，MOEA/D-TPN 容易找到边界解。对于F2 测试问题，MOEA/D-DE、MOEA/D-STM 和MOEA/D-TPN三个算法获取到解的精度基本相同，但是MOEA/D-TPN 的收敛速度最快。F3、F4 和F5 三个测试函数极其复杂，具有长尾和尖峰区域，MOEA/D-DE 仅在POF 中部区域上找到一部分解，MOEA/D-TPN 在边界区域也能寻找到一部分解。对于更复杂的三目标优化问题F6，MOEA/D-TPN 也表现出了更优越的寻优性能。

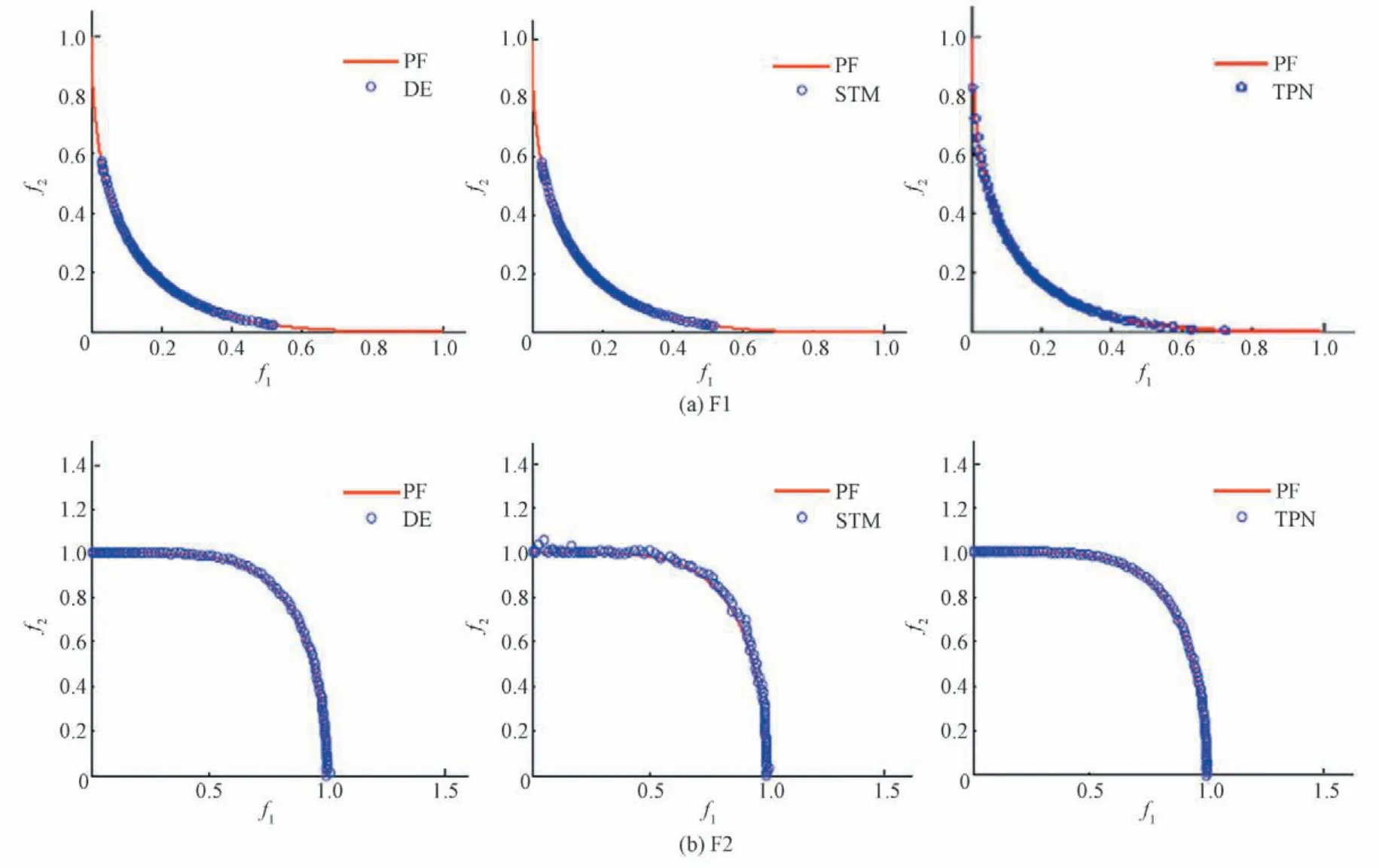
图3 3种算法的逼近结果Fig.3 Approximation results of three algorithms

图4给出了3种对比算法30次独立运行取得最小IGD 值时的演化曲线。可以看出，对于F1-F6 测试函数，与MOEA/D-DE和MOEA/D-STM 相比，MOEA/D-TPN 的进化曲线均表现出较快的收敛速度和较好的逼近精度。

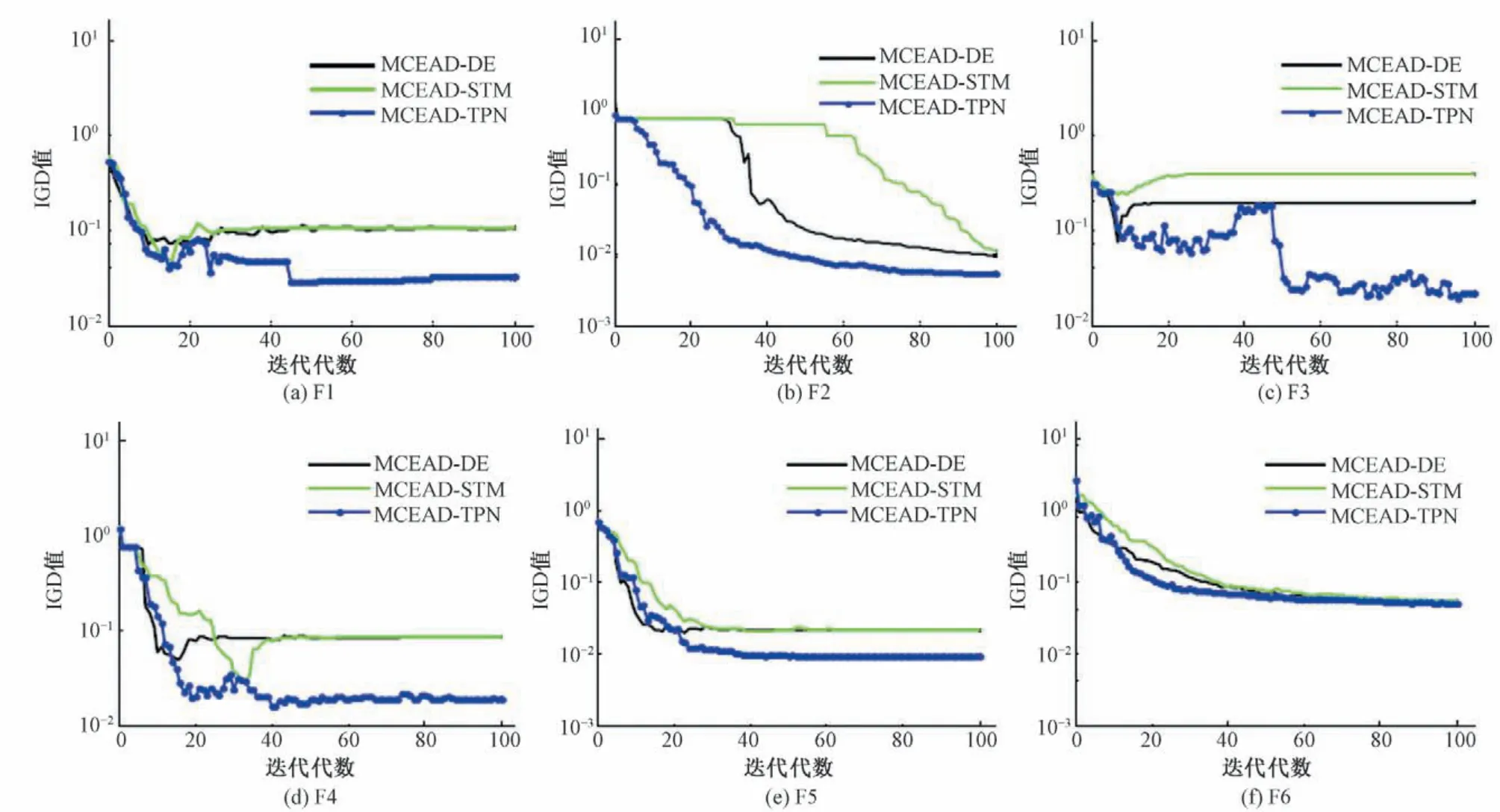
图4 3种算法的IGD进化曲线Fig.4 IGD evolution curve of three algorithms

图5 给出了3 种对比算法30 次独立运行绘制的IGD 盒形图。可以看出，对于F1、F3、F4 和F5 四个测试函数，MOEA/DTPN的IGD总体处于较低范围，分布性好，寻优性能突出。对于F2 和F6，MOEA/D-TPN 与MOEA/D-DE、MOEA/D-STM 的性能相当，略占优势。

图5 3种算法的IGD盒形图Fig.5 IGD box diagram of three algorithms

4.4 供水管网优化

下面利用所设计的MOEA/D-TPN 算法对双环管网的造价（经济性）和节点富余水头总和（可靠性）两个目标进行优化。MOEA/D-TPN 的参数设置同上。图6 给出了MOEA/D-TPN 算法获取到的Pareto 前沿。每一个Pareto 解对应的决策空间变量是［x1，x2，x3，x4，x5，x6，x7，x8］，分别表示双环管网的8个管径。

图6 管网的Pareto前沿Fig.6 Pareto front of pipe network

本文设计一种基于模糊隶属函数的智能决策方法，利用该方法能够在Pareto 前沿上决策出一个折衷解，从而获得8 个管径的一个最佳组合。首先利用模糊隶属函数定义第i个目标函数fi的Pareto解xk的满意度，如下：

其中，fmaxi和fmini分别代表第i个目标函数fi的最大值和最小值。然后， 可以计算出xk的规范化隶属度函数μk，如下：

其中，m为目标函数个数，|S|是算法获得的Pareto 解集的元素个数。本文选取μk为最小值时的解，即可图6中的折衷解。

从图6中可以看出，MOEA/D-TPN能够获取更多的边界解。此时，从边界中进行取值能够取得经济性和可靠性的最佳平衡。

从图6 的Pareto 前沿中选取25 个解，列出决策变量和目标函数的取值，如表3所示。可以看出，管网造价和节点富余水头总和之间存在冲突特性。随着管网造价的逐步升高，节点富余水头总和越来越低，表明总造价增大的同时，故障率逐步降低，可靠性逐步增大；反之总造价减少的话，故障率逐步抬高，可靠性逐步降低。这在管网施工时就会产生冲突，施工方一方面期望能尽量降低总造价，另一方面也期望故障率尽可能地低，可靠性尽可能地高。利用MOEA/D-TPN 决策出的最优解将能够在保证足够可靠性的前提下尽量降低成本，为城市供水管网优化设计提供有益参考。

表3 算法获取的Pareto解Tab.3 Pareto solutions obtained by algorithm

5 结 语

本文提出一种自适应MOEA/D 算法，命名为MOEA/DTPN，利用其解决城市供水管网多目标优化设计问题。为了平衡MOEA/D 解的多样性和分布性，设计了两阶段策略和小生境引导策略。利用6 个具有复杂Pareto 前沿的测试函数进行了算法性能验证，并与MOEA/D-DE、MOEA/D-STM 等多个先进算法进行了比较，在4 个测试函数中MOEA/D-TPN 的寻优结果最好，在其余两个测试函数中性能表现相当。根据我国供水系统的运行情况，利用城市供水双环官网模型进行了仿真测试，确定了总造价和故障率两个冲突的目标函数，运用MOEA/D-TPN算法对管网进行多目标优化设计，求解出双环管网的最优解集。下一步工作是利用本文设计的MOEA/D-TPN 解决大型复杂管网的多目标优化问题。