轨道交通超高顺坡率变化的缓和曲线盾心平面坐标计算及盾心曲线拟合方法
朱礼佳
(上海市政工程设计研究总院(集团)有限公司,200092,上海∥工程师)
轨道交通车辆经过曲线段时会产生离心力。为了平衡离心力,提升乘坐舒适度,曲线段轨道需设置超高。曲线段轨道超高值(以下简称“超高值”)一般在缓和曲线内递减,其超高顺坡率不宜大于2‰。由于存在轨道超高,车辆会产生倾角,在盾构区间内,车辆中心线就会偏离盾构中心线,这种偏移即为盾心偏移。在设计过程中,可将该偏移量提前计入盾心坐标中,使盾构中心线与车辆中心线重合,从而提高盾构掘进准确度,降低后期调线调坡难度。
超高顺坡率恒定的缓和曲线盾心坐标计算方法已相对成熟。然而,在实际设计过程中,受城市建设条件的限制,常会遇到缓和曲线侵入站台的情况。对此,设计规范明确要求:在车站站台有效长度范围内,超高值不应大于15 mm[1-2]。由此可知,当站台端处超高值超过15 mm时,进站前后的缓和曲线超高顺坡率不同。对于超高顺坡率变化的缓和曲线,常规的三次抛物线拟合曲线往往难以满足设计精度要求。对此类缓和曲线的盾心坐标计算及曲线的拟合分析也尚未有相关研究。本文利用构建等效模型的方法得到超高顺坡率变化的缓和曲线任意点盾心偏移平面坐标的计算方法,通过优化拟合模型提升盾心曲线拟合精度,得到轨道交通盾心曲线拟合优度的判断方法,以期为各类轨道交通设计及盾构施工提供理论支撑。
1 顺坡率固定的缓和曲线坐标计算
一般情况下,缓和曲线上的超高顺坡率是固定值,在求得缓和曲线线路平面坐标后,结合盾心偏移量,即可求出缓和曲线盾心平面坐标。
1.1 盾心平面偏移量的计算
单圆盾构盾心偏移断面如图1所示。由几何关系可以求得盾心横向偏移量e为:

图1 单圆盾构盾心偏移断面示意图
e=Hh/S
(1)
式中:
H——轨面至盾心距离;
h——轨道超高量;
S——轨距。
1.2 线路平面坐标计算
为方便计算,以直缓点为原点,建立绝对坐标系。则绝对坐标系下的缓和曲线盾心偏移如图2所示。设曲线半径为R,缓和曲线总长度为L,缓和曲线上任意点λ的平面坐标为(x,y),λ与直缓点间的缓和曲线长度为l。

图2 绝对坐标系下缓和曲线盾心偏移示意图
利用泰勒级数展开,并根据轨道交通设计精度要求取其前两项后,得到点λ的线路平面坐标(x,y)为[3]:
(2)
1.3 盾心平面坐标计算
对于点λ对应的横向偏移量δ可由超高引起的横向偏移量求得:
δ=el/L=Hhl/(SL)
(3)
设点λ处缓和曲线切线与X轴夹角为α,其中α=l2/(2RL)。将sinα及cosα进行泰勒级数展开并取其前两位为有效精度值。那么超高顺坡率固定情况下缓和曲线盾心平面坐标(xa,ya)可以表示为:
(4)
2 顺坡率变化的缓和曲线盾心计算
2.1 缓和曲线上任意点的超高
对于超高顺坡率变化的缓和曲线,其平面线路坐标与超高顺坡率无关,故线路平面坐标计算方法与一般情况相同。
由式(1)可知,缓和曲线进站前后超高不同,e也不同,故盾心坐标会随e的变化而变化。为便于计算,本文以直缓点为原点,以l为自变量,超高为因变量,即可得到超高顺坡率固定和超高顺坡率变化时的缓和曲线h-l关系如图3所示,其中ρ0为固定超高顺坡率,ρ1为超高顺坡率有效站台外顺坡率,ρ2为有效站台内顺坡率,lx为有效站台边缘与直缓点间的缓和曲线长度,hm为最大轨道超高值,h0为有效站台边缘处的轨道超高值,且有0≤h0≤15 mm。
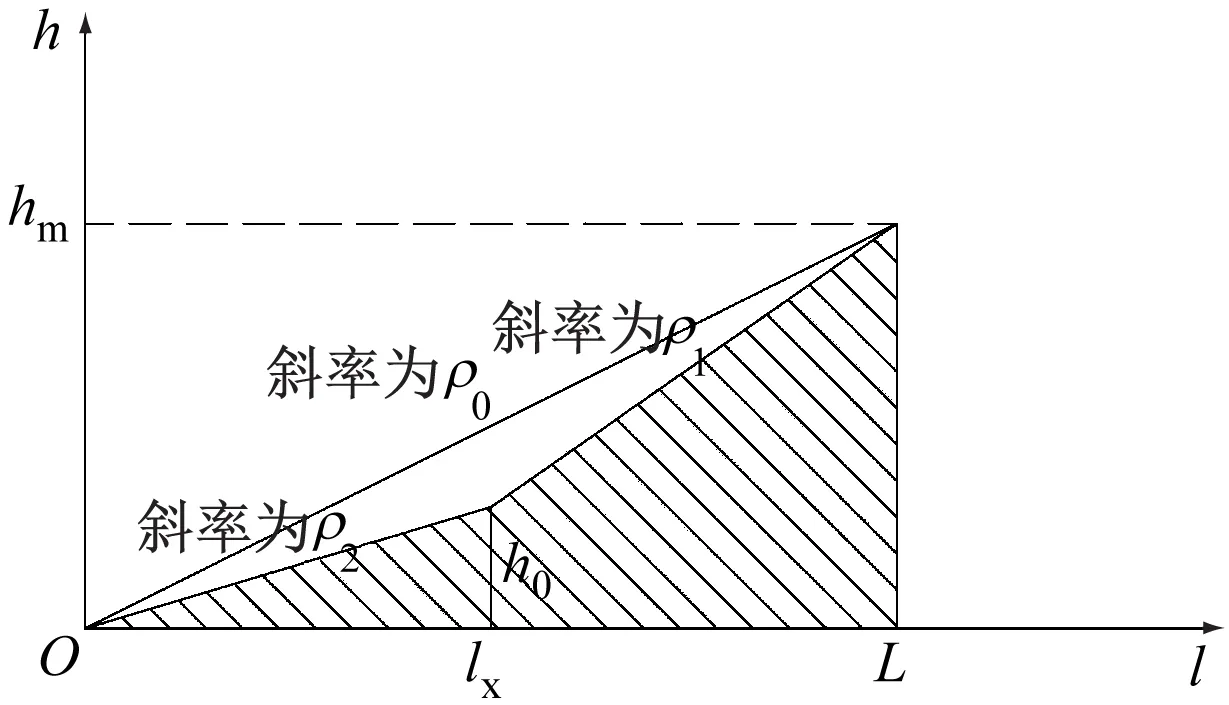
图3 缓和曲线h-l关系图
2.2 构建等效缓和曲线
本文采用构建等效缓和曲线的方法计算lx—L段原缓和曲线的偏移盾心坐标。考虑到原缓和曲线平面上各点对应曲率不同,等效缓和曲线需保证原缓和曲线的平面参数不变。由于超高顺坡率变化点位于站台边缘,不在直缓点上,其对应的缓和曲线曲率非零,故不可将该段缓和曲线简单等效为顺坡率为ρ1、缓长为(L-lx)的缓和曲线。
将该段缓和曲线等效超高为hm+hb,缓长为L,超高顺坡率为ρ1的缓和曲线。等效缓和曲线的h-L关系如图4所示。此时该段缓和曲线的盾心坐标即为该等效模型中等效缓和曲线盾心坐标减去由虚拟超高hb产生的偏移量在x和y轴上的分量。
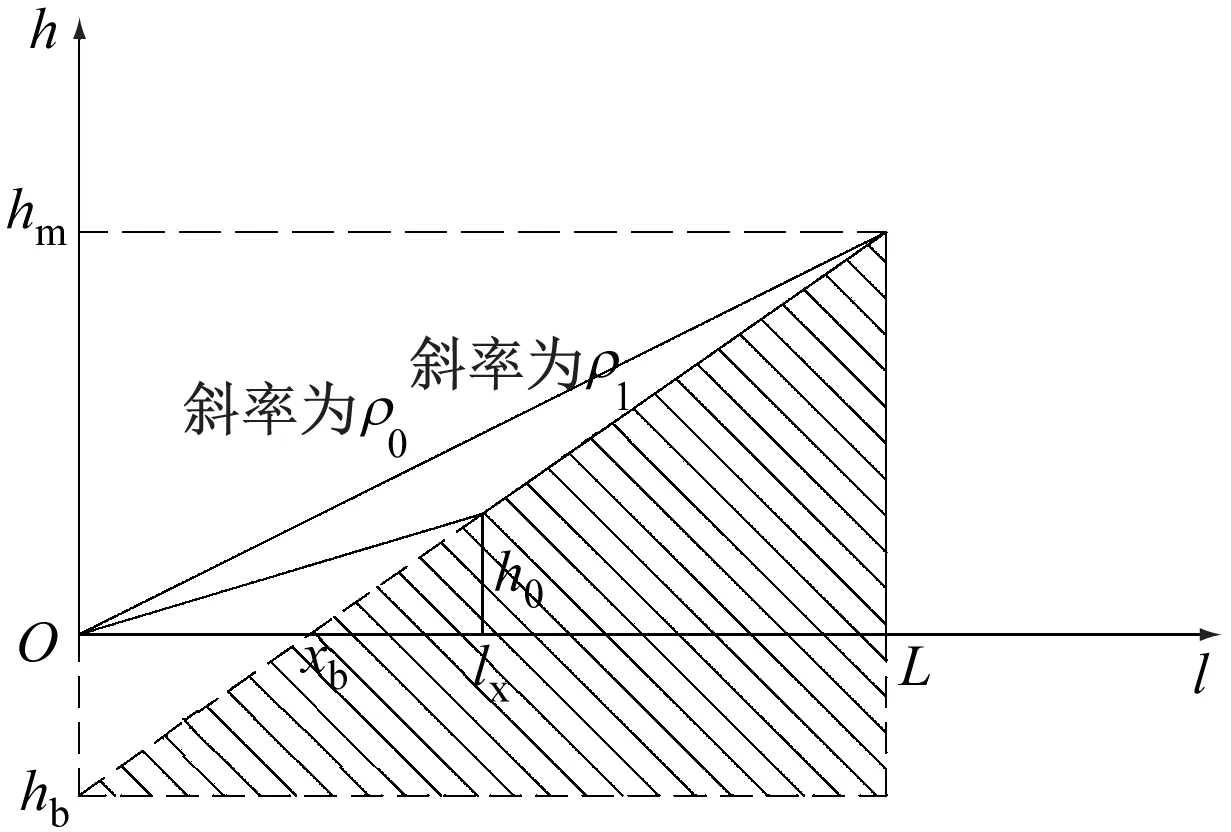
图4 等效缓和曲线h-L关系图
由图4可求得,等效缓和曲线与横轴的交点横坐标xb=(hmlx-h0L)/(hm-h0),则虚拟超高hb=h0xb/(lx-xb),由hb产生的偏移量eb=Hhb/S,由(hm+hb)而产生的偏移量ec=H(hm+hb)/S。由此,对于等效缓和曲线上任意点λc,其对应的横向偏移量δc可以表示为:
δc=lec/L=Hl(hm+hb)/(LS),lx≤l≤L
(5)
由此可知,lx—L段缓和曲线上任意处的盾心平面坐标(xc,yc)为:
(6)
3 超高顺坡率变化的缓和曲线盾心拟合
对于超高顺坡率固定的缓和曲线,通常采用三次抛物线来拟合盾心曲线;对于超高顺坡率变化的缓和曲线,采用三次抛物线拟合一般会导致盾心拟合结果误差较大。
3.1 盾心拟合曲线优度评价
本文对盾心坐标离散点进行线性回归拟合,并引入统计学决定系数R2来评价回归模型的拟合优度。R2可表示为[4]:
R2=sSR/sST=1-sSE/sST
(7)
式中:
sSR——回归平方和;
sSE——残差平方和;
sST——离差平方和。
一般情况下,R2越接近1,缓和曲线拟合的效果越好。但随着离散点样本量的增加,盾心拟合方程的R2必然随之增加,另一方面,个别离散点产生的较大误差不一定能够准确反馈至R2,两者并不是正相关的。故利用R2无法真正定量说明拟合方程的准确程度,只能大概对拟合的好坏进行定性分析。
(8)

若设计过程中的精度要求为拟合曲线与实际盾心坐标的绝对误差不大于Ea,那么由于四舍五入的关系,实际各点盾心坐标与拟合曲线间的绝对误差应控制在Ea/2内。假设对于任意满足拟合误差精度要求的缓和曲线,以Δl为步长取得的所有离散点盾心坐标与拟合曲线间的绝对误差为ε,并分别取Ea/2、3Ea/8、Ea/4、Ea/8作为特征点,建立误差绝对值域权重集合φ={a,b,c,d},其中a、b、c和d分别为误差绝对值于[3Ea/8,Ea/2)、[Ea/4,3Ea/8)、[Ea/8,Ea/4)和(0,Ea/8]内的离散点占比,且有a+b+c+d=1。
对《地铁设计规范》[1]和《市域(郊)铁路设计规范》[2]中的各标准缓和曲线进行拟合以分析误差,其中地铁以设计最高速度为80 km h的标准计算,市域铁路以设计最高速度为160 km/h的标准计算,暂不考虑欠超高及过超高影响。设最大允许拟合误差Ea为1 mm,并将步长设置为1 m,取其中最大绝对误差值大于Ea/8且小于等于Ea/2的缓和曲线进行整理,并总结得到各离散点误差绝对值域的权重,如表1—表2所示。

表1 地铁拟合误差较大缓和曲线参数表

表2 市域(郊)铁路拟合误差较大缓和曲线参数表
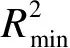
(9)
式中:
φm——地铁的数据残差权重;
φs——市域铁路的数据残差权重。
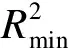
(10)

(11)
3.2 案例分析
本文以上海轨道交通市域线崇明线工程(以下简称“崇明线”)中一处缓和曲线为例进行分析。崇明线某处线路平面示意图如图5所示。该线为市域铁路,最高设计时速为120 km,有效站台范围内最大超高不大于15 mm。图5中SJD11缓和曲线侵入车站有效站台范围内的长度lx约为31.173 m,其曲线半径R为500 m,缓和曲线长度L为115 m,超高值hm为135 mm,有效站台内顺坡率ρ2为0.481,有效站台外顺坡率ρ1为1.432,轨面至盾构中心距离H为2 150 mm,轨距S为1 500 mm。

图5 崇明线某处平面线路示意图截图
3.2.1 拟合优度判断区间

3.2.2 三次抛物线拟合分析
根据已知的线路条件,由式(6)可以求得SJD11缓和曲线上任意点λc的盾心平面坐标(xc,yc)为:
(12)
在该段缓和曲线上选取n个离散点,以第k离散点与直缓点间的缓和曲线长度lk构成集合li={l1,l2,…,lk,…,ln}。由于31.173 m≤lk≤115.000 m,以1 m为步长取值,即li={32,33,…,115}。根据式(12)的计算结果,求得li上各点相应的盾心平面坐标,再通过最小二乘法对离散坐标点进行曲线拟合。采用三次抛物线拟合,得到等效缓和曲线的拟合方程f3(xc):
f3(xc)=-0.053 095 9+2.659 16×10-3xc-
(13)
选取若干典型离散点坐标,与li={32,33,…,115}对应的yc和f3(xc)计算结果进行对比,进而分析误差。三次抛物线典型离散点误差分析表如表3所示。由表3可见,三次抛物线拟合后,局部离散点绝对误差大于0.5 mm,不满足设计要求。这与拟合优度判断结果一致。
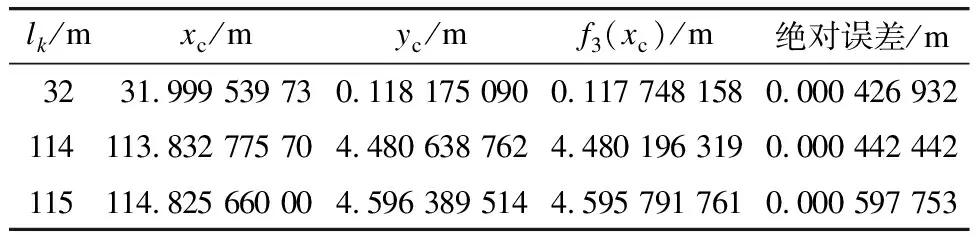
表3 三次抛物线典型离散点误差分析表
3.2.3 四次曲线拟合分析
将拟合函数优化为四次曲线进行计算分析。其等效缓和曲线拟合方程f4(xc)如式(14)所示。
f4(xc)=-0.036 032+0.001 563 26xc+
(14)
针对li={32,33,…,115}求出对应的yc和f4(xc),选取拟合结果中误差较大的典型离散点坐标进行比对分析,得到四次曲线典型离散点误差分析表如表4所示。增加拟合阶数后,最大误差由原三次抛物线的约0.6 mm降低至四次曲线的约0.1 mm,说明该拟合曲线方程满足设计要求。
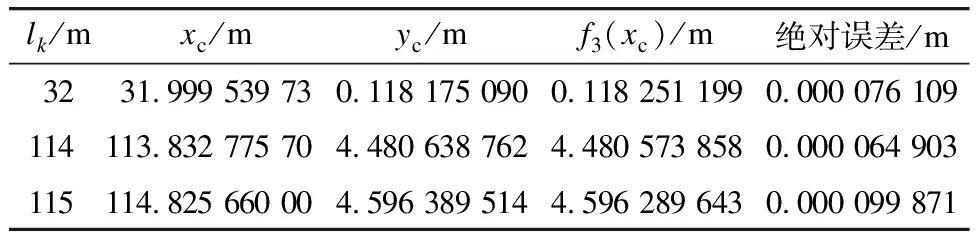
表4 四次曲线典型离散点误差分析表
4 结语
本文研究了超高顺坡率变化的缓和曲线盾心平面坐标计算方法及其盾心曲线拟合方法,对缓和曲线盾心坐标计算方法进行了完善。该盾心曲线拟合方法更适应目前轨道交通的设计现状。通过本文的等效缓和曲线法可准确计算超高顺坡率变化的缓和曲线盾心平面坐标。本文基于盾心拟合曲线最大误差,计算误差绝对值域权重集合,进而判断拟合优度,检验盾心拟合曲线的校正决定系数,对拟合精度是否满足要求进行定性判断,以此决定是否需要优化拟合模型,从而有效提高设计效率及设计质量。

