基于射频指纹的自适应变分模态分解算法*

文 璐 张琰祥 王 鹏 惠 鏸 姚俊良

(1.中铁第一勘察设计院集团有限公司,710043,西安; 2.西安理工大学自动化与信息工程学院,710048,西安∥第一作者,高级工程师)

0 引言

现有城市轨道交通列车运行控制系统主要依赖于无线通信,而其通信环境中存在大量外部干扰信号,对列车运行安全产生严重威胁。2012年11月乘客携带的便携式Wi-Fi(无线保真)路由器产生了干扰,导致深圳地铁2、5号线多次中断运行。对此,可利用无线通信设备的RFF(射频指纹)对城市轨道交通环境中的无线发射设备进行身份识别,进而及时发现外部干扰源。这对保障城市轨道交通安全具有重要意义[1]。

RFF的概念由Hall等人首次提出[2],指由无线设备硬件差异所导致的射频信号细微差异。随后涌现出大量通过RFF对无线发射设备进行身份识别的研究[3-5]。研究表明,有效提取能够表征设备本质特征的RFF对提高识别准确率起到关键作用。VMD(变分模态分解)算法[6]可将信号自适应地分解为不同中心频率的窄带分量,从而获得设备的RFF特征。2019年文献[4]首次将VMD算法应用于RFF识别领域。之后文献[5]探究了该算法在不同信噪比下识别准确率的性能边界。文献[7]利用VMD算法提取信号时频谱中的定向梯度直方图作为RFF,其识别准确率较文献[4]的算法准确率得到了进一步提升。

根据上述研究,在IMF(本征模态函数)个数K和惩罚因子α较为准确的前提下,VMD算法具有良好的RFF提取能力。然而,如果K和α不准确,则可能出现模态混叠现象和过分解等问题。对此,文献[8]提出了S-VMD(连续变分模态分解)算法,采取逐次分解的方式寻找合适的K值;文献[9]则以分解后各模态分量与原信号之间的相关系数为依据选定K值。总体来说VMD算法中分解参数的选取尚处于探索阶段,且现有研究主要集中于K值的选取,鲜有对α值的选取研究。

对此,本文提出了一种改进的VMD算法——自适应VMD算法。该算法利用分解后各模态之间的相关系数及各模态能量在信号总能量中的占比来判断分解中是否出现了频率混叠现象和过分解问题,并通过迭代方式选取合适的K和α,可有效提高设备的识别准确率。

1 自适应VMD算法

1.1 模态函数的相关系数与能量占比

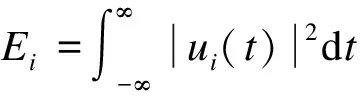
(1)

假设信号f(t)的幅值A=0.25 mV,其频率fn分别为50 Hz、100 Hz、150 Hz、400 Hz等4个不同频率,则当信号受到了噪声污染时有:

(2)

式中:

n0——加性高斯白噪声。

在理想情况下,VMD算法能够还原出原始的4个频率分量,即K的理想值应为4。本文基于此,分析K和α取值不同时,cij及pi受到的影响。

1.1.1K小于理想值

设K=3、α=100,对f(t)进行VMD算法分解,得到各本征模态函数的频谱图如图1所示,cij和pi如表1所示。观察图1发现,模态u1(t)与u2(t)在100 Hz左右出现了明显的频率混叠现象。进一步观察表1发现,与之对应的c21=0.064较高。这说明K值设置过小会造成模态混叠,且cij能较好地反映是否出现了模态混叠。因此,定义cmax=max(cij),i≠j;且cmax值应小于某混叠门限τc。cmax≥τc说明出现了模态混叠现象,需要增大K值。

图1 K=3、α=100时的本征模态函数频谱图

表1 K=3、α=100时的cij和pi

1.1.2K取理想值,α偏小

取K=4、α=100,得到本征模态函数频谱图如图2所示,cij和pi如表2所示。观察图2发现,模态1与模态2的混叠现象并没有消失。表2中c21仍然较高,且图2在300 Hz左右出现了实际信号中并不存在的频率分量——伪模态u3(t),说明出现了过分解问题。相比于其他模态,u3(t)的能量占比p3=0.126显然偏小。结合K的理想取值为4进一步分析可发现:①K的设置合理但α的设置不合适,仍然无法获得良好的分解结果;② 通过pi可以发现过分解问题。为防止过分解,定义pmin=min(pi)应大于某占比门限τe,pmin≤τe说明出现了过分解。在本试验中,既出现了模态混叠又出现了过分解,不是因为K设置不合适,而是需要增大α,在更小的尺度上进行模态提取。

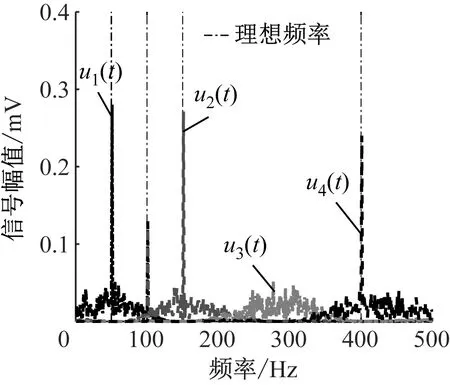
图2 K=4、α=100时的本征模态函数频谱图

表2 K=4、α=100时的cij和pi

1.1.3K取理想值,α增大

取K=4、α=600,得到本征模态函数频谱图如图3所示,cij和pi如表3所示。由图3可见,模态混叠和过分解现象消失了,说明准确分解出了信号的4个本征模态函数。由表3可见,此时各模态之间的相关系数普遍较低且各模态能量占比无明显差别。由此可知,只要cmax<τc且pmin>τe,就可以认为分解结果满足要求。大量仿真试验还表明,α只要大于一定值就能满足分解要求。本文限于篇幅未将仿真结果一一列出。

图3 K=4、α=600时的本征模态函数频谱图

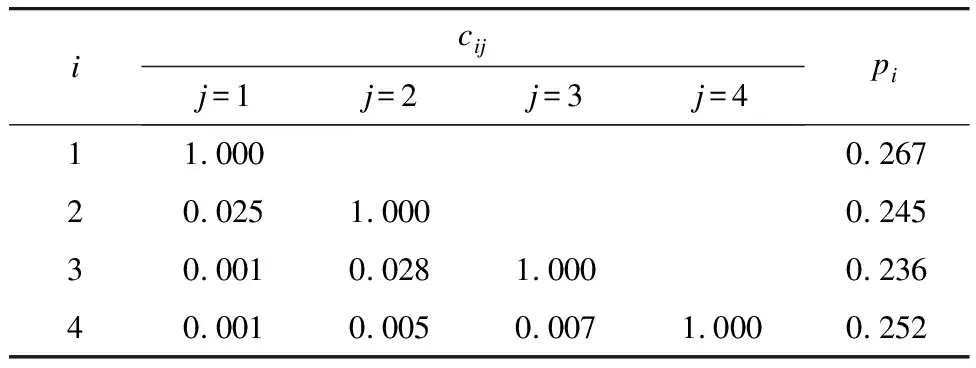
表3 K=4、α=600时的cij和pi

1.1.4K大于理想值

取K=5、α=600,得到本征模态函数频谱图如图4所示,cij和pi见表4。观察图4可知,K值过大导致出现伪模态4。由表4可见,p4明显偏小。由此判断,当pmin≤τe单独出现时应减小K。

图4 K=5、α=600时的本征模态函数频谱图

表4 K=5、α=600时的cij和pi

1.2 自适应变分模态分解算法流程

结合K及α取值情况,自适应VMD算法流程如图5所示。对信号f(t)进行K阶VMD处理并求得cmax和pmin,以此判断分解过程中是否出现了模态混叠或过分解现象,并以迭代方式不断调整分解参数,最终输出合适的K和α。

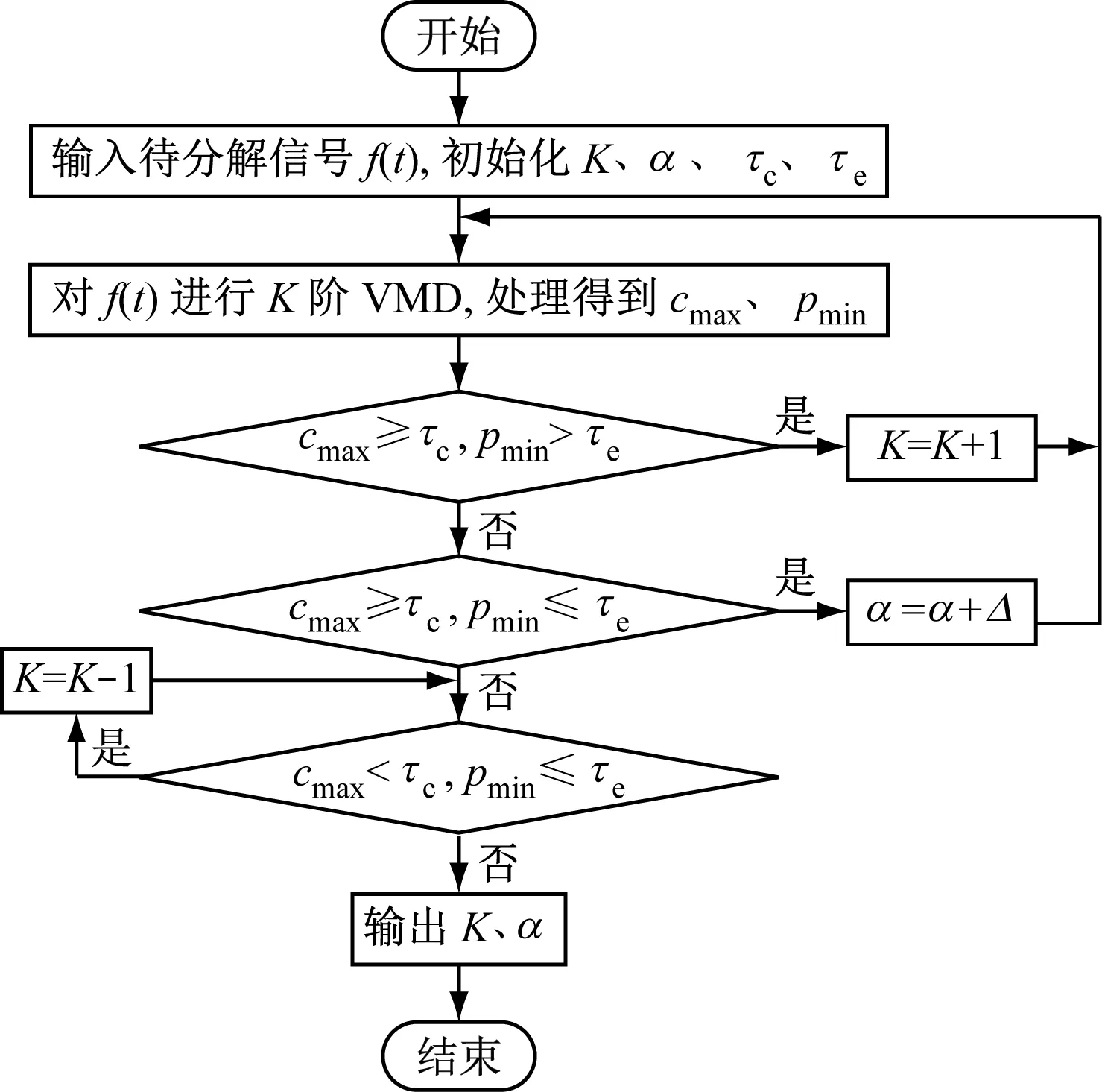
注:Δ为α的递增量。

2 算法的识别性能

采用自适应VMD算法对式(2)中的f(t)进行分解,得到K=4、α=600。分解前后信号的时域和频谱波形如图6所示。由图6可见,重构信号与原始信号的4个本征模态函数构成一致,说明分解结果准确可靠。与原信号相比,重构信号不但信号特征,即RFF保留完整,且噪声得到了一定程度的抑制,说明本文算法具有较强的RFF提取能力。

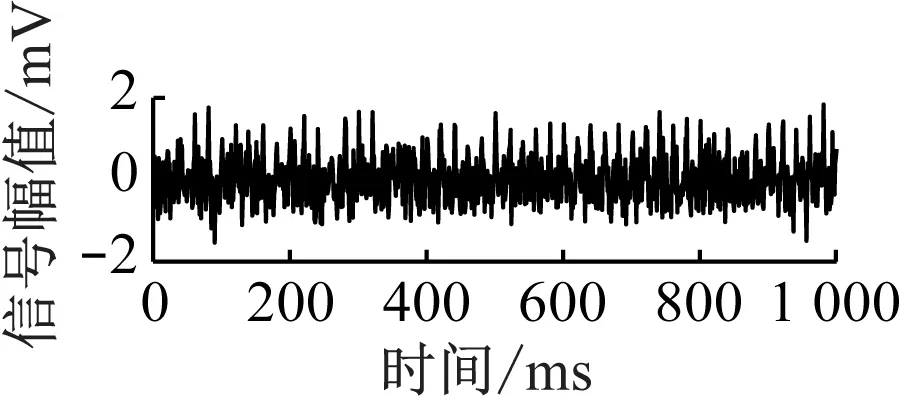
a) 原始信号时域波形

为进一步验证自适应VMD算法对实际设备的识别性能,本文对WiSig数据集[10]中来自20台不同Wi-Fi设备的信号进行识别。每台设备取200帧,每帧取前256位,将数据集划分为70%的训练集、10%的验证集和20%的测试集。构建LSTM(长短期记忆网络)对设备进行分类识别。LSTM由LSTM层、全连接层和输出层组成。其中:LSTM层有256个神经元;全连接层采用Leaky ReLU函数作为激励函数,并采用Softmax进行分类。选用Adam优化器,批量大小为64,初始学习率为0.001,轮次设置为400。试验使用Matlab R2020b软件,CPU(中央处理器)为Intel酷睿i7-11800H,GPU(图形处理器)为NVIDIA GeForce RTX 3060。

为验证识别准确性,本文应用自适应VMD算法进行信号分解识别,并同原始VMD算法及S-VMD算法识别结果进行比较。其中,自适应VMD算法和S-VMD算法的分解参数由算法自动求取,原始VMD算法的分解参数分别为K=9、α=900和K=3、α=300。识别准确率曲线如图7所示。

图7 识别准确率曲线

由图7可见,与S-VMD算法及原始VMD算法相比,自适应VMD算法的识别准确率明显最高,特别是在信噪比较低时,自适应VMD算法的识别准确率仍表现较好;在不同分解参数下,原始VMD算法的识别准确率差别较大,说明分解参数的选择对原始VMD算法的分解结果及识别准确率有很大的影响。对于原始VMD算法,其参数固定,很难根据不同设备的特性来灵活调整K和α。自适应VMD算法可按不同设备特性来自适应选取不同的分解参数,故具有较强的适应性和较高的识别准确率。

当信噪比为10 dB时,采用自适应VMD算法与S-VMD算法得到的分类混淆矩阵如图8所示。

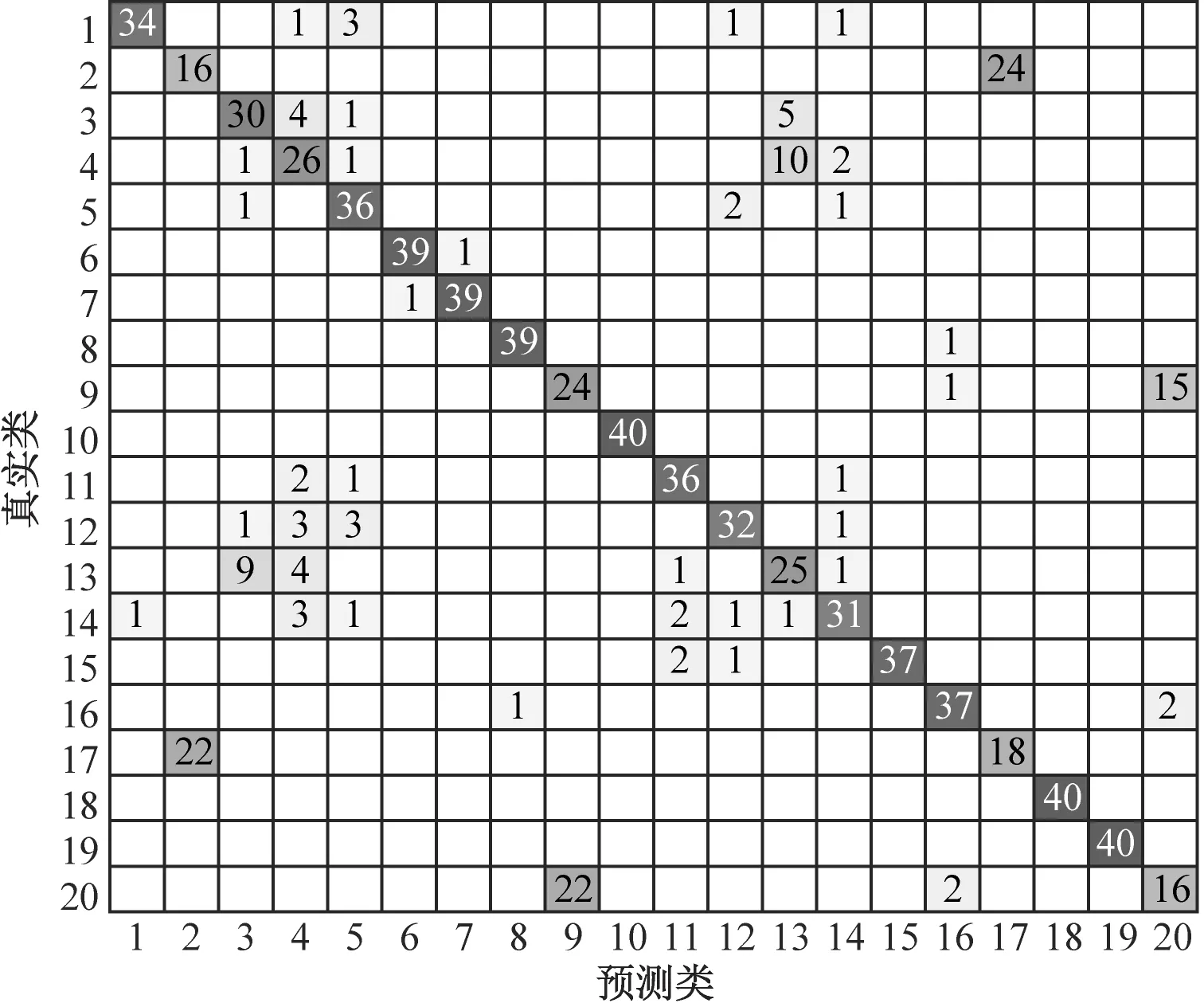
a) 自适应VMD分类混淆矩阵

由图8可以看出,在噪声影响下,S-VMD算法对设备的误识别率较高,自适应VMD算法对设备的误识别率较低,说明其受噪声影响程度较轻。由此可见,自适应VMD算法提取的RFF更能反映设备本身的特性。

3 结语

本文提出自适应VMD算法提取无线发射设备的RFF,对城市轨道交通无线通信环境中的发射设备进行识别。算法利用不同模态之间的相关系数判断分解过程是否出现了模态混叠现象,利用各模态与原信号的能量占比判断是否出现了过分解,并通过迭代方式确定合适的模态分解数和惩罚因子。该算法可针对不同设备自适应获取合适的分解参数,有效避免了模态混叠及过分解问题对RFF提取的影响,具有良好的自适应性和噪声鲁棒性,可有效提高设备的识别准确率。