微电网源网荷储分布鲁棒优化调度方法研究

何玉朝，郭枫，钱辉敏，姚胜红，张能

（国网电力科学研究院武汉南瑞有限责任公司，湖北武汉 430074）

随着微电网的不断发展，微电网的结构也在发生着巨大的改变。目前，复杂的微电网已经成为研究热点，其在电网中的地位日益突出。微电网的发展使电力系统在经济和可靠性方面取得了良好的发展。

当前，在微电网群中，最优的排序模型大多是单一的，大多数微电网络的优化调度策略仅能达到单个的目的，并不能提高微电网的稳定性和降低系统的运营成本。随着我国分布式电力系统渗透率的不断增加，电力系统总体运行效率较低，源网荷储各个环节之间协调不够，各类电源互补互济不足的问题越来越突出。对源网荷储进行分层分区平衡处理，能够有效解决地域资源网络负载大和存储效果不佳的问题。

关于电力微电网的运行优化问题已较为成熟。当前，我国已经形成了一种新型的电力枢纽模型，该模型能够有效地增强电力系统的适应性，并能够有效地降低可再生能源的消耗。与此同时，通过构建能源枢纽模型，能够均衡源网荷储负载，有效调度微电网[1]。相关学者还提出了一种多电网功率优化控制模型，该模型针对可再生能源数据的异构以及一次能源不确定引起的出力控制问题，建立了多网最优控制模型。通过控制微电网源网荷储分布的负荷，实现微电网的有效调度[2]。然而，针对电力系统规划、调度与运行的研究多以系统运行与资源最优组合为重点，单纯使用上述两种方法缺乏对微电网的需求与控制。

针对以上研究的不足，该研究提出了微电网源网荷储分布鲁棒优化调度方法。

1 微电网源网荷储分布鲁棒优化调度模型

1.1 分布鲁棒优化调度目标函数

针对微电网源网荷储分布鲁棒优化调度，需构建分布鲁棒优化调度目标函数，优化调度模型可以实现两个目标：最小费用和最小污染物排放量，基于此，构建的优化调度目标函数为：

式（2）中，εS、εY、εN分别表示二氧化硫、烟尘和氮氧化物的排放系数[3-4]。通过上述这两个公式，能够控制成本和污染物排放量，为分布鲁棒优化调度提供数据支持。

1.2 约束条件

各种发电机组的发电功率不得高于或低于其额定功率，由此设置的约束条件可表示为：

式（3）中，ΔWm、ΔWg、ΔWf分别表示火电机组m、光伏g和风机f在理想情况下初始出力到最大出力的差值；vm、vg、vf分别表示火电机组m、光伏g和风机f在运行周期内运行速率的最小值[5]；分别表示火电机组m、光伏g和风机f在运行周期内运行速率的最大值。

微电网发电是一种极具随机特性的电力系统，在不弃风、弃光的前提下，通过引入多台灵活、可调的发电机组，使其能够充分利用其互补、协同的特点，达到协同控制的目的[6-8]。在此基础上，通过需求端的资源转移，使用电量达到相对可控状态，保证电力供需双方相互适应、相互协调。

1.3 调度模型构建

针对分布式电源接入配电系统的相关技术要求，结合微电网的辐射运行特点和保护配置原理，提出了在计划阶段采用变电站变压器低压侧开关、变电站低压母线输入开关、配电变压器高压侧开关的调度结构[9-10]。在此基础上，根据微电网的层级定义，构建了“源网荷储”分层分区平衡调度模型，如图1所示。

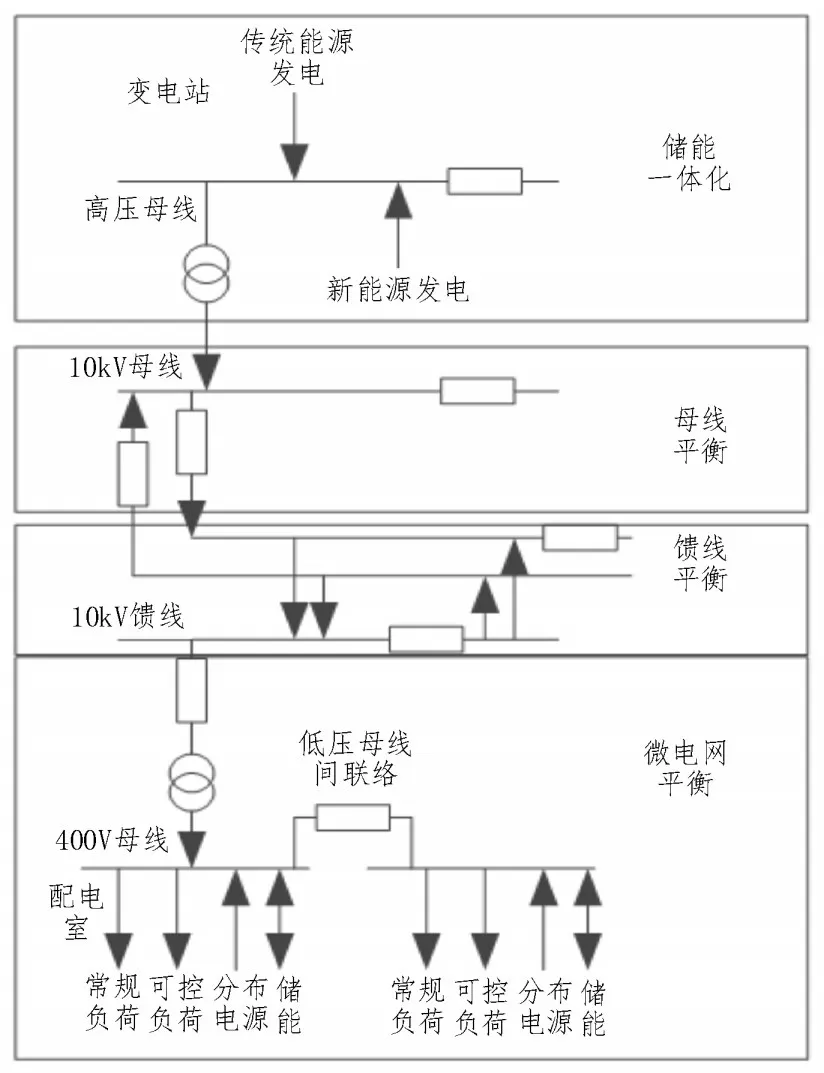
图1 分层分区平衡调度模型

图1 中，该模型主要包括4 个部分，分别是储能一体化、母线平衡、馈线平衡和微电网平衡[11]。其中，高压母线、10 kV 母线、10 kV 馈线、400 V 母线为微电网潮流控制的4 个节点，需满足线路最大供电需求以及单向潮流的约束条件，防止电流倒送现象的发生。

2 模型求解

2.1 基于粒子群优化求解

粒子群是一种通过多次迭代而获得的随机解，这种方法属于多目标优化问题，而传统粒子群算法只能求一个解[12]。针对多目标优化问题，常将各目标函数按权重划分为一个整体目标函数，并用粒子群优化算法进行求解[13]。

采用收缩因子的粒子群算法对微电网源网荷储分布鲁棒进行优化调度，以求得高质量解。速度更新公式为：

式（4）中，vk、vk+1分别表示粒子经过第k、k+1 次迭代处理后的速度；η1、η2均表示迭代收缩因子；s1、s2表示实数分别表示粒子到目前为止最佳位置、粒子当前所在位置、粒子全局最佳位置[14]；β表示收缩因子。在此基础上，各指标权重会不断地改变，且微粒群也会随之改变。该算法能使不可行的系统运行方案在可行区域内被迅速地排除，加速了算法的收敛性[15]。

在求解时，采用归档机制对非主要解进行跟踪。在优化调度目标函数中，主要任务就是对已知的未占优势解进行追踪。与此同时，为保持所发现的问题，一般使用文档来选取全局最优位置和个别最优位置。归档机制，“全局向导”与“个人向导”被称为全局最佳解和个体最佳解[16]。在引入归档机制的基础上，可以在保持最佳解集多样性的前提下，使算法的计算速度得到最大程度改善。具体计算过程如下：

步骤1：定义迭代次数最大值，从而实现群体随机初始化；

步骤2：确定个体极值、初值和全局极值，通过求解各个粒子的自适应度，得到非支配解集合。粒子在每次迭代过程中，粒子群的位置更新是由粒子群适应性函数来确定的，其表达式如下：

式（5）中，p表示采样点；F表示调度模型函数；UM表示约束函数。

步骤3：对外部文件集进行更新，按粒子拥挤程度依次递减，并删除不占比例非控解；

步骤4：采用迭代法求出粒子速度、位置，并对已有粒子群进行更新，调整各个粒子的极值，并进行修正；

步骤5：将新的非劣解加入外部文件，产生新的外部文件，并求出新的全局极值；

步骤6：如果已经得到了最大迭代数，就会结束搜索，如果不能，则返回到步骤2。

由于该方法属于多目标优化问题，因此，粒子群算法可获得最优解，且最优解为系统的运行成本最低。

2.2 源网荷储分布鲁棒优化调度决策方案

微电网能量优化的目标是使可再生能源和各种资源得到最大程度的利用，并按“源网荷储”进行有序调度，从而达到最大的经济效益。能量互补关系示意图如图2 所示。

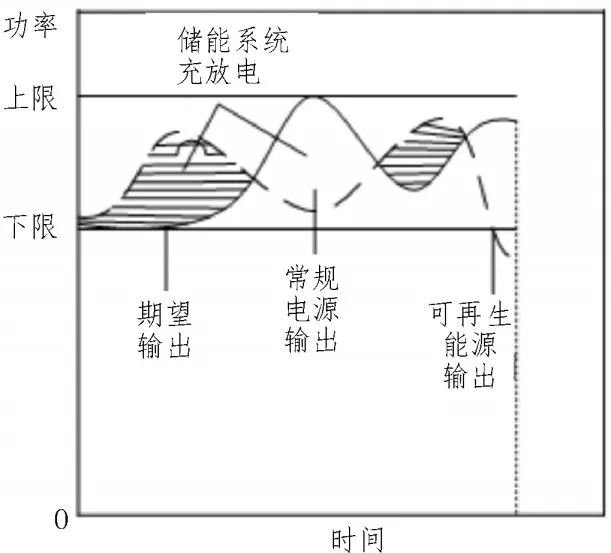
图2 能量互补关系示意图

图2 中，使用能量互补模式能够实现全局优先全额调度，在满足上述调度模式的情况下，剩余的可再生能源将用于蓄能系统充电，然后将其转移到可调度的负载中进行消纳处理。在电力系统不能满足微电网负载要求的情况下，通过储能系统和交互功率的联合决策，达到最佳的调度。

3 实验与分析

3.1 场景设置

以华北某地区的发电厂为例，该地区微电网主要包括的参数内容如下：

光伏阵列额定功率依次为30、20、15 kW；风机额定功率依次为30、20、10 kW；蓄电池容量为100 kW·h、充电率为90%、放电率为95%；柴油机额定功率为120 kW、燃油成本系数为0.2、排放系数为220。

在实时电价下，利用微电网内部分布式能满足微电网内部的负荷需求。各机组出力理想情况如图3 所示。由图3 可知，光伏理想功率在运行时间为6～8 h 时，达到最大值为40 kW；风机理想功率在运行时间为6～8 h 时，达到最大值为20 kW；蓄电池理想功率在运行时间为5.5～8.5 h 时，达到最大值为35 kW；柴油机理想功率在运行时间为6～8 h 时，达到最大值为20 kW。

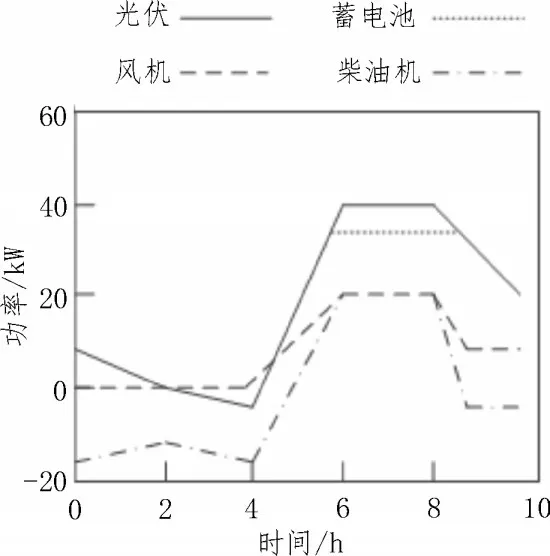
图3 各机组出力的理想情况

3.2 实验结果与分析

分别使用基于能量枢纽模型、多电网功率优化控制模型和分布鲁棒优化调度方法，分析各机组出力是否达到理想情况，对比结果如图4 所示。

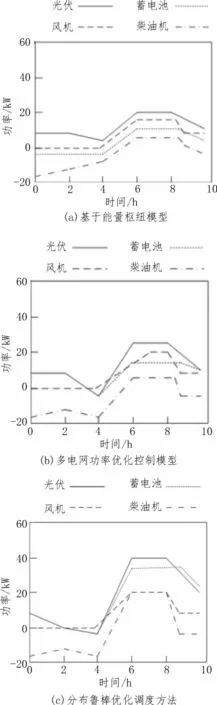
图4 三种方法各机组出力对比分析

由图4（a）可知，光伏理想功率在运行时间为6～8 h 时，达到最大值为20 kW；风机理想功率在运行时间为6～8.5 h 时，达到最大值为16 kW；蓄电池理想功率在运行时间为6～8.5 h 时，达到最大值为10 kW；柴油机理想功率在运行时间为6～8.5 h 时，达到最大值为6 kW，使用该方法光伏、风机、蓄电池、柴油机的出力情况均与图3 所示数值不一致。

由图4（b）可知，使用该方法光伏、风机、蓄电池、柴油机出力情况均与图3 所示数值不一致，光伏理想功率在运行时间为6～8 h 时，达到最大值为25 kW；风机理想功率在运行时间为7～8 h 时，达到最大值为20 kW；蓄电池理想功率在运行时间为5.5～8.5 h 时，达到最大值为14 kW；柴油机理想功率在运行时间为6～8.5 h 时，达到最大值为6 kW。

由图4（c）可知，使用该方法光伏、风机、柴油机出力情况均与图3 所示数值一致，只有蓄电池理想功率在运行时间为6～9 h时，与理想出力时间相差1 h。

通过上述分析结果可知，使用分布鲁棒优化调度方法调度效果最佳。

4 结束语

该研究提出了一种微电网源网荷储分布鲁棒优化调度研究方法，该方法通过分布鲁棒优化调度方式达到电力负荷相对可控的目的，并建立了一种“源—网—荷—储”的优化调度模型，根据发电量的相对可控性来满足电力用户需求，从而实现最优调度。