基于加权正则化极限学习机与改进梯度投影法的谐波源定位

沈清野

（国网舟山供电公司，浙江 舟山 316000）

0 引言

随着高渗透率的分布式电源接入电网，同时大量的非线性负荷在配电网中的占比增大，配电网中的谐波污染日趋复杂，世界各国均予以高度重视[1-2]。配电网中产生的大量谐波不仅危害家用电器设备的正常运行，甚至会损害设备，而且在严重时可能造成重大的电网安全事故。因此，急需对配电网的谐波源进行有效定位以快速消除系统中的大量谐波，保证系统的安全稳定运行[3]。目前，谐波源定位方法可以划分为两类：一类是等效电路法，该方法的优点是模型比较简单，缺点是仅能判别谐波源是位于系统侧还是负荷侧，不能实现谐波源的精确位置及谐波电流的准确估值，且多数情况下应用于单谐波源的定位；另一类是谐波状态估计法，该方法仅需安装少量的量测装置就可实现系统的整体可观性，其广泛应用于多谐波源的定位研究[4]。文献[5]采用基于压缩感知的谐波检测器来识别和估计系统中的主谐波源，该方法不受背景谐波的影响，可有效进行主谐波源的识别及谐波电流的估计。针对谐波状态估计法中嫌疑节点的选取问题，本文进行了探讨。

1 监测装置优化配置

为了平衡系统可观性及控制成本之间的矛盾，下面将通过构建系统监测装置最优配置的模型（包括目标函数和约束条件）及优化求解方法（模拟退火遗传算法）来解决。

1.1 目标函数

设n节点系统目标函数为

其中，n表示所选系统的节点总数；ξi表示在节点i安装量测装置的成本，本文不考虑量测装置间的差异，取ξi=1；ηi的取值有1和0，当其为1时表示该节点装有监测装置，当其为0时表示该节点未安装监测装置。

1.2 约束条件

通过如下方法可判断系统中的节点是否可观。

a）当某条母线安装量测装置，则与其相连支路电流均为可测量。

b）当一条支路中的一个端点配备量测装置，或者除节点i的电压未知，而与节点i相连的其他节点的电压已知，则另一个端点或节点i的电压可虚拟测量。

c）当一条支路两端电压确定，或者若某节点连接y条支路，其中已知y-1条支路的电流，则可虚拟测量该支路电流。

构建描述系统节点的关联矩阵M，矩阵中元素表示方法为

系统可观测性的约束方程可表示为

其中，η=[η1，η2，…，ηn]T，表示每个节点的量测装置配置情况；I表示每个节点至少有一个量测装置可观测到，其矩阵元素都为1。

为确定系统量测装置的数量和位置，本文采用模拟退火遗传算法SA+GA法[6]（simulated annealing and genetic algorithm）对上述模型进行求解。

2 谐波源定位原理

基于上述监测装置优化配置结果，下面将分别进行谐波源的定性分析及定量分析。谐波源的定性分析选择加权正则化极限学习机WRELM（weighted regularization extreme learning machine）估计器的谐波源定性分析，谐波源的定量分析选择改进梯度投影法IGPM（improved gradient projection method）的谐波源定量分析。

2.1 基于WRELM估计器的谐波源定性分析

在单隐含层前馈神经网络的基础上，有学者提出了极限学习机ELM（extreme learning machine）算法，利用ELM较强的非线性拟合特性构造谐波源定位估计器，进行谐波源的定性分析。

设ELM模型具有K个隐含层神经元，激活函数为g（x），则定位估计器模型为

其中，和分别表示输入、输出向量与隐含层i的连接权值向量；bi为隐含层i的偏置值；为ELM网络的输入集。

本文在ELM估计器的基础上引入正则化系数、加权系数及结构风险，构建WRELM谐波源定位估计器，以提高估计器的泛化能力和估计精度，详细步骤如下：

a）构建WRELM估计器目标函数。设其函数为

其中，γ为正则化系数；为隐含层输出矩阵；为训练样本的误差和；为输出集；为权重的对角矩阵；分别为经验风险和结构风险。

b）根据式（5）可构建目标函数的Lagrange方程，具体情况如式（6）所示。

其中，α为拉格朗日算子。

d）将式（7）代入式（4）即可得到WRELM估计器的拟合回归模型。

基于上述步骤则可建成WRELM估计器。

2.2 基于IGPM的谐波源定量分析

通常配电网中的谐波源数量较少，且状态分布稀疏，因此可基于压缩感知理论进行谐波源定位。梯度投影法在采样点有限的条件下具有精确度高、鲁棒性强的优点，但由于其采用交替搜索方式，造成运算复杂度高、速度慢。为提高谐波源定位的速度，节约存储空间，将梯度投影法的搜索方式改为沿负梯度方向，可降低算法的计算量，并提高其泛化能力。因此，本文采用IGPM[7]进行谐波源的定量分析。

为验证IGPM定量分析的结果，本文以经典谐波源定位方法即最小二乘法LSM（least square method）作为对比进行仿真。

a）LSM定位原理。设系统含有n个节点，则由各节点之间的谐波电压向量与注入电流向量可列写如下系统状态方程。

若忽略非嫌疑节点的谐波注入电流，则通过式（10）可得嫌疑节点的注入谐波电流。

式（11）即为LSM进行谐波源定位的计算方程。

b）IGPM定位原理。设IGPM的目标函数为

将上述目标函数进一步变换为求解凸非约束优化问题

IGPM的搜索方向和搜索步长的计算方法如下：设第k次迭代的支撑集、重构向量及信号残差分别为、和rk-1。为使每次迭代后的重构向量的稀疏性最高且重构误差最小，将式（13）展开得到

欲使式（14）取值最小等价于求解式（15）

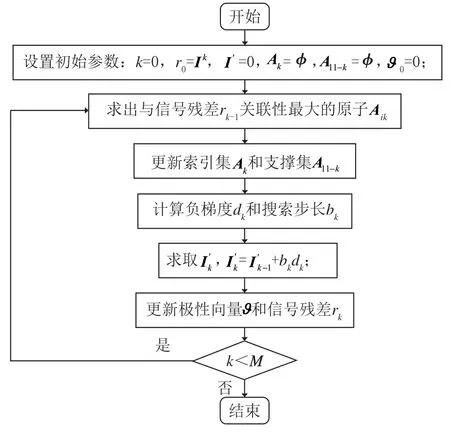
图1 求取重构向量流程图

为衡量谐波源定量分析结果的准确性，选用相对误差e1作为评价指标，其公式如下。

其中，zi表示第i个谐波源注入节点的谐波电流值。

3 算例分析

在PSCAD仿真平台搭建IEEE14节点系统对提出方法进行验证，其具体相关参数依据文献[8]进行设置。仿真实验使用的数据均从该仿真系统获取，具体方法如下：

首先将文献[9]中5次谐波电流源的经典曲线加入到仿真系统；然后不断改变谐波电流源的位置，记录量测装置在每个状态过程中检测到的谐波电压幅值和相位；最后，将记录的谐波监测点电压参数向量及谐波源所处母线的位置向量一一对应组成数据对，作为定位器的训练数据集。基于该方法共采集了320对数据组成训练数据集。仿真中使用的训练数据与分析数据相互独立。

3.1 量测装置数量及分布

以IEEE14节点系统为例进行仿真。采用SA+GA对1.1小节及1.2小节构建的量测装置优化配置模型进行求解，初始化控制参数如下：种群P=10个，最大遗传代数M=100，交叉概率Pc=0.7，变异概率Pm=0.01，冷却系数q=0.8，起始温度To=100 ℃，终止温度为Tend，进化代数t=120，各计算14次，配置结果如表1所示。

表1 两种算法的配置结果

从表1可以看出，与SA相比，SA+GA不仅在全局收敛性方面性能表现优良，而且其所需配置的量测节点的数目也较少，即仅需在节点A2、A6及A9安装量测装置即可实现系统的全局可观测。

3.2 WRELM的参数选择

将量测节点的电压向量作为WRELM输入，谐波源所在节点编号作为输出，构建WRELM定位估计器。以错误率作为评价指标，在3.1节的监测装置获取的数据选择120组仿真数据作为测试样本，基于交叉验证法来进行WRELM估计器的参数选取，仿真结果如表2所示。

表2 参数优化结果

从表2可以看出，当WRELM估计器的激活函数为Sine，隐含层个数为20层时，其具有最高的正确率。

3.3 监测点优化配置效果分析

为了考察监测装置分布对谐波源定位结果的影响，采用构建的WRELM定位估计器对安装不同数量监测点的系统进行单谐波源定位效果分析。仿真使用180组数据进行测试，WRELM定位估计器的隐含层选用20层，激活函数选用Sine，定位效果如表3所示。

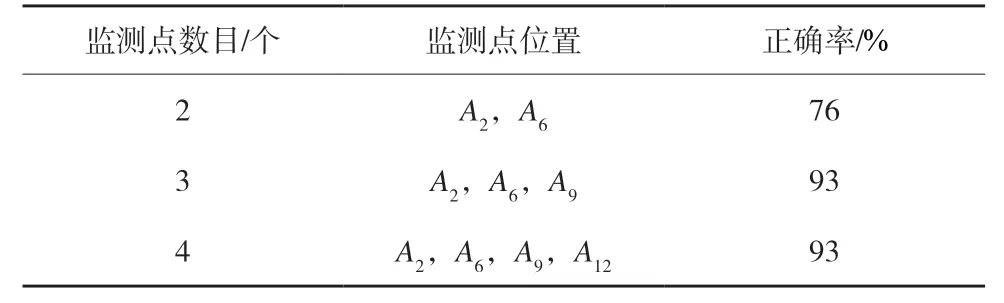
表3 不同监测点数目对定位效果的影响

从表3可以看出，当监测点位置选用SA+GA优化分布最优时（即监测点位置在A2，A6，A9），和当监测点位置选用SA的最优配置方案时（即监测点位置在A2，A6，A9，A12），定位估计器的正确率一致，均为93 。由于安装监测装置的费用较高，考虑经济因素，故本文选取的监测点数目为3个。

3.4 WRELM估计器定位结果分析

为了验证该定位估计器的定位效果，在同样的仿真环境中，分别构建BP估计器、ELM估计器作为对比进行谐波源的定性分析。对比3种定位估计器的训练时间，结果如表4所示。

表4 不同估计器的训练时间

从表4可以看出，相比其他2个模型，WRELM估计器的训练时间最短。当监测点数目增加时，3种方法的样本训练时间均有所增加，但是WRELM估计器的训练时间仍较其他2种方法更短。

根据方案1配置量测节点，随机选取不同数量情况下谐波源的安装位置，以50组测试样本为例，验证表4中的3种定位估计器的定位效果，定位结果如表5所示。

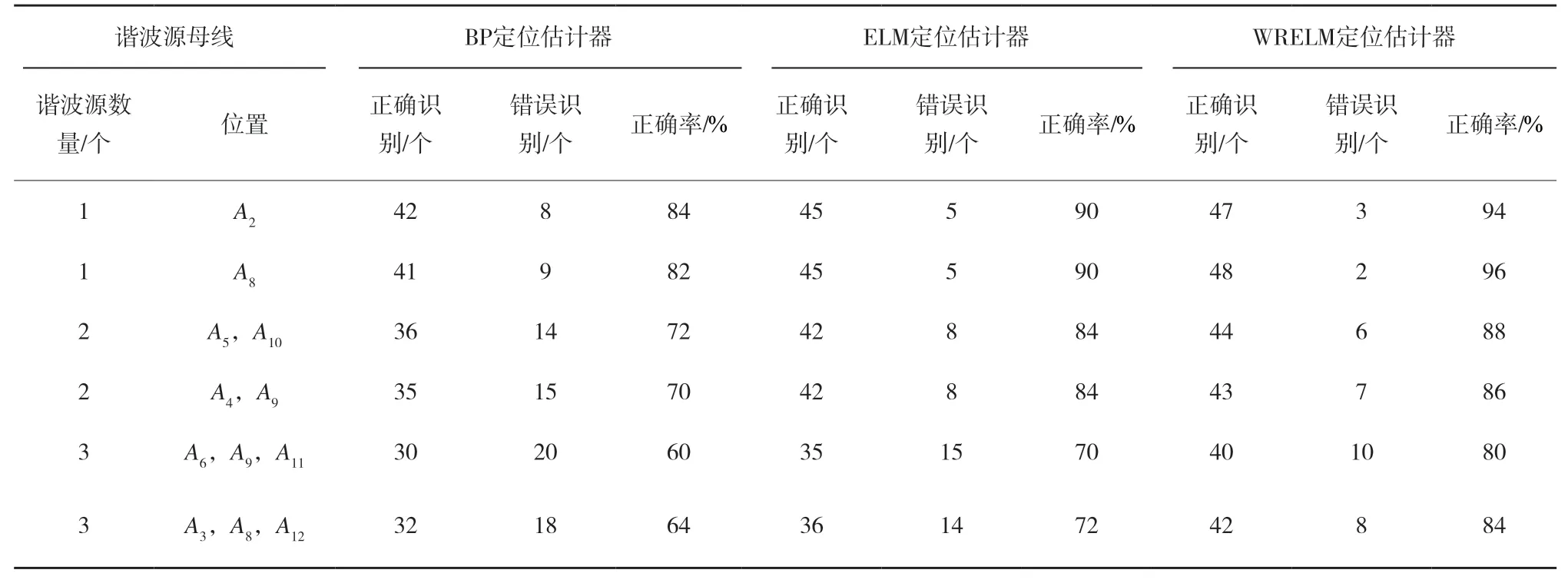
表5 3种估计器的定位效果

由表5可知，与构建的BP估计器相比，ELM估计器定位的准确率更高，而WRELM估计器的准确率较ELM估计器有进一步的提高，表明对ELM网络进行优化有助于提高其泛化能力。

3.5 IGPM定位结果分析

为验证IGPM定位分析效果，我们在系统中的不同节点分别设置了含有1个及3个5次谐波电流源谐波源时的情况为例进行仿真。在具体的分析过程中，首先根据WRELM估计器估计出的嫌疑节点及3个监测母线获取的支路谐波电流测量数据，然后再采用IGPM进行谐波源定位的定量分析。定量分析结果如表6所示。

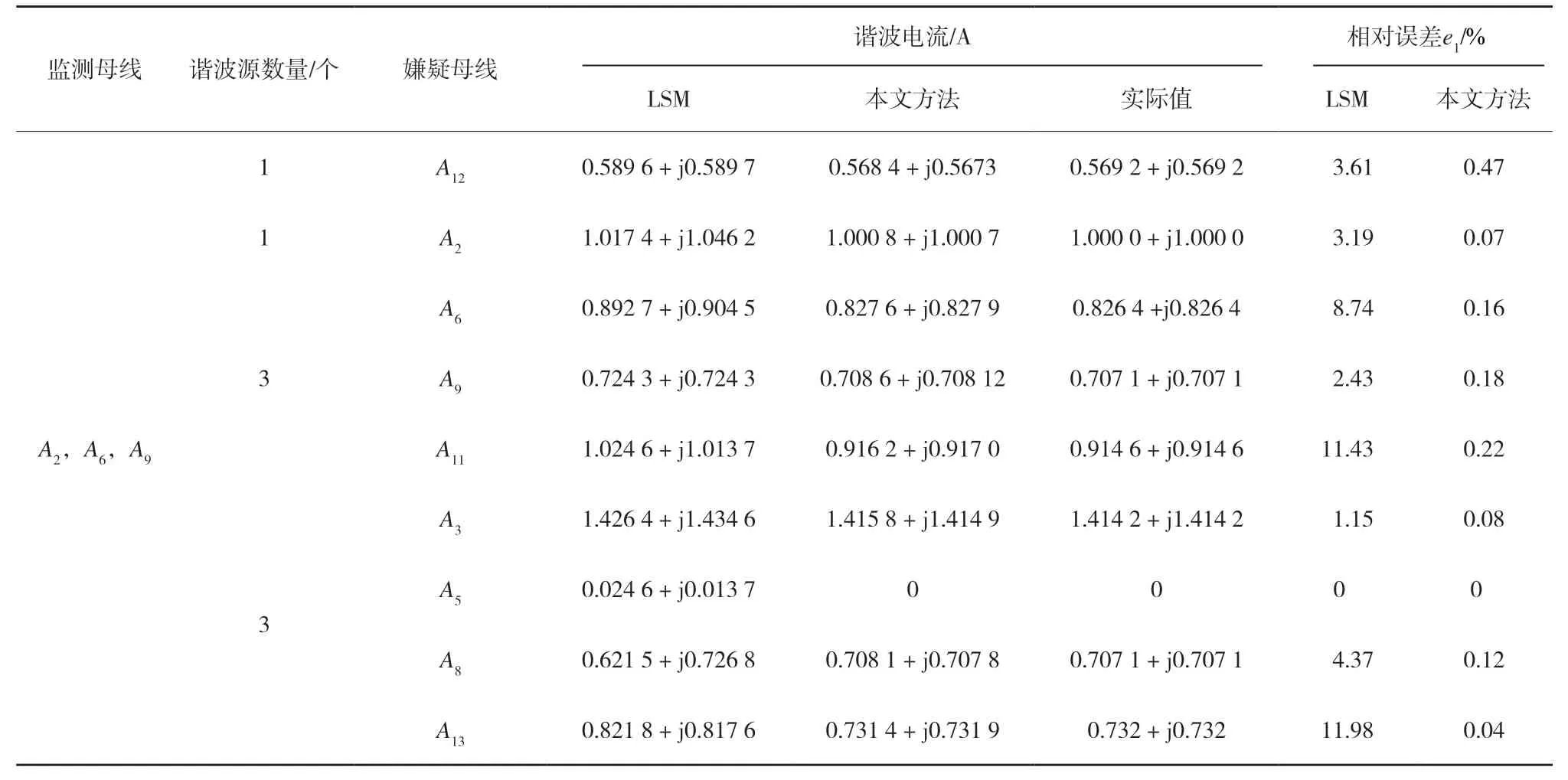
表6 多谐波源定位结果

从表6可看出，与LSM相比，IGPM定量分析的结果与实际值更为接近，相对误差更小，准确度更高。这是由于IGPM搜索方式的改进，不仅降低了计算量，而且提高了梯度投影法的泛化能力。当系统中含有多个谐波源时，WRELM定位估计器可能存在谐波源误判现象，但是其可准确地划定嫌疑节点存在的范围，为谐波源定位定量分析奠定基础。在含有多个谐波源时，与LSM相比，IGPM不仅可准确地计算出谐波电流值，而且可对WRELM估计器的定性结果进行验证，且计算结果与实际值相吻合。

4 结论

提出采用WRELM与IGPM相组合的方法开展谐波源定位，得出以下结论：

a）为验证WRELM估计器的定性分析效果，在同一仿真环境中，分别构建BP、ELM定位估计器与其进行对比，仿真结果表明WRELM估计器不仅计算速度快，而且定性分析结果准确度更高。

b）根据WRELM估计器给出的嫌疑节点范围，分别采用LSM和IGPM定量分析嫌疑节点的注入谐波电流。与LSM相比，IGPM可更加准确地完成谐波源的定量分析，精度更高。