一道解几质检题的探究、溯源与推广*

安徽省芜湖市第一中学 (241000) 孙川越 刘海涛

《高考评价体系》指出:高考要从“知识立意”转向“能力立意”,考查学生的“关键能力”和“核心素养”.这就要求学生在学习中,学会灵活运用所学知识分析、解决问题,达到从“解题”向“解决问题”的转变.在解析几何问题中,有一类圆过定点问题,背景实为两相交直线斜率之积为定值,笔者通过曲线系法高效处理该类问题,并将问题一般化推广,以帮助读者在高考备考中掌握该类问题的模式化解题策略.

1 问题呈现

2 解法探究

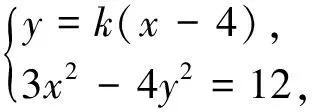
当直线l斜率不存在时,l:x=4,点E与点M重合,点F与点N重合,不妨设E(4,3),F(4,-3),则以EF为直径的圆的方程为(x-4)2+y2=9,显然过定点(1,0)和(7,0).

综上,以EF为直径的圆恒过定点(1,0)和(7,0).

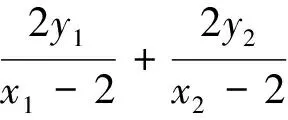
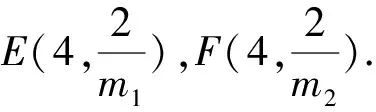
3 试题命制的背景

由上述解法2,不难明白该题的命制背景是:已知圆锥曲线C:f(x,y)=0与x轴(或y轴)的交点A(顶点),过x轴(或y轴)上一定点F(异于点A)的直线与曲线C交于D,E两点,直线AD,AE与垂直于x轴(或y轴)的直线l(l不过点A)分别交于M,N两点,则(1)直线AD,AE的斜率积为定值;(2)以MN为直径的圆是否恒过x轴(或y轴)上的两个定点.

4 试题的溯源

事实上,对于上述圆过定点的问题,早在2014年的福建数学联赛预赛和2019年的北京卷中就分别以椭圆、抛物线为背景考查过.

解析：(1)x=4(过程略).

题3 (2019年北京卷·第18题)已知抛物线C:x2=-2py经过点(2,-1)．(1)求抛物线C的方程及其准线方程;(2)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=-1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.

解析：(1)易得C:x2=-4y,准线:y=1.

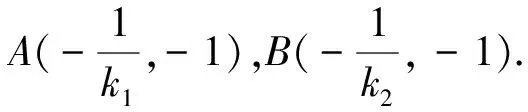
5 问题的推广

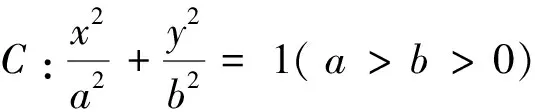
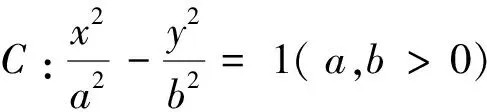
问题3 已知抛物线C:y2=2px(p>0),过点F(t,0)(异于坐标原点O)的直线交抛物线C于D,E两点,直线OD,OE与直线l:x=m(m≠0)分别交于M,N两点,以MN为直径的圆是否恒过x轴上的定点?

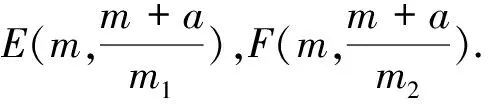
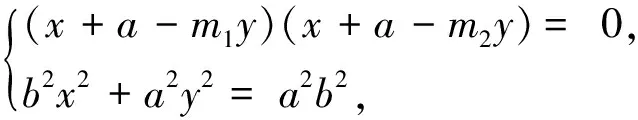
基于此,得到如下结论:

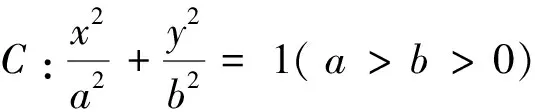
问题2的探究类同问题1,并且同样地可得到如下结论:

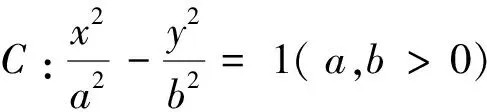
对问题3的探究也可得到: