一种优化后的混沌置乱图像加密算法

刘迪　樊匀

关键词：优化；混沌；随机置乱；RGB分量；标记；相关性

中图分类号：TP309 文献标识码：A

文章编号：1009-3044（2023）20-0020-03

0 引言

随着大数据、5G网络、人工智能的高速发展，图像的网络传输是人们传达信息的重要手段之一。由于网络的公开性，图像传输过程中如果不进行加密处理，很容易暴露关键信息，有可能引发诸如个人隐私或者重要机密泄露等极其严重的后果，因此信息安全与信息保密工作刻不容缓，图像加密技术是多年来的重要课题之一。在众多加密方法中，由于混沌具有初始值的敏感性、随机性、不确定性、不可预测性等优秀的特性，十分适合图像加密，由此国内外学者掀起了基于混沌加密技术研究热潮。近几年来，王庆杰等人[1]提出了Logistic Map-Chebyshev Map的组合加密算法；曾珂等人[2]提出了基于 3D-LSCM 的混沌加密算法；纪元法等人[3]提出了基于Logistic-Sine的彩色图像加密算法；王潇[4]提出了一种基于混沌的空域彩色图像复合加密算法；Mohammad Ahmar Khan等人[5]提出了混沌遍历性和正弦映射相结合的图像加密技术。一个较理想的图像加密算法应当具备复杂度低、安全性高并具有一定的抗攻击能力等优点，因此本文在基于Logistic映射加密算法的基础上，分别在RGB三个分量上利用随机置乱实现了彩色图像的加密和解密过程，同时针对加密传输过程可能受到的图像缺损攻击，提出了一种简单高效的优化方案，令其还原度更高。通过Matlab仿真平台的实验证明：该算法复杂度低，密钥安全性好且还原度高，并具有较好的抗缺损攻击能力。

1 算法原理

1.1 混沌序列加密的算法

混沌序列的加密算法过程可以这样描述：首先由混沌系统产生一个混沌序列，与明文逐位异或后得到密文，而这个产生的混沌序列转化成二进制后就是加密的密钥。其加解密原理图如图1所示：

1.2 置乱技术

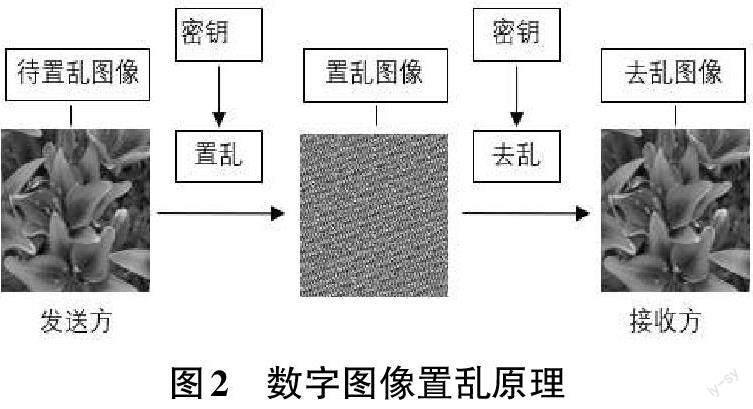
如果将数字图像看成是一个m×n的矩阵，通过一系列矩阵的各类运算，将打乱矩阵的排列，那么对应数字图像的像素也会被打乱，从外观上看便会失去原本的识别度，即实现了图像加密的目的。比如最经典的Arnold置乱算法（猫脸变换）便是基于此原理[6]。置乱加密的原理如图2所示[7]。由于彩色图像的置乱变换原理与灰度图像并没有本质上的区别，因此同样适用。

2 加密算法与解密算法

2.3 优化后的抗缺损解密算法

考虑到加密图像在网络传输过程中有可能遭受裁切或者涂抹攻击，造成缺损。如果是小面积缺损对还原后的图像质量影响不大，但如果是大面积缺损，则将严重影响还原质量，甚至造成重要信息的识别不清。因此，为提高图像的抗缺损攻击能力，本文在解密算法基础上进行了优化设计：当图像进行随机置乱后，相邻像素的相关性会变得很小，因此出现多个连续相同数值的相邻像素概率极低，如果发生这种情况，基本可判定为图像遭受了较为严重的攻击，出现了较大面积的缺损；本文设定当系统检测到出现有3个相邻像素值相等的情况，即可判定为此处图像缺损，便对此处做出标记，当检测出多个类似情况，均做出标记；待到图像解密完成后，这些标记便会回到原始图像的各个位置，根据原始图像相邻像素相关性很高的原理，可以取每个被标记位置周边的像素值平均值，并以该平均值替换掉被标记的像素即可，该方法从理论上可大大提高图像的还原程度。

3 检验与分析

3.1 图像像素的相关性

在正常的数字图像中，相邻像素的数值往往比较接近（排除色彩分界线等少数极端情况），因此数字图像的置乱效果好与坏，通常可以通过分析其相邻像素之間的相关性来反映。如果相邻像素之间的相关性越小，说明置乱效果越好；而反之，则说明置乱的效果越差。图像相邻像素之间相关性的计算通常用到下面两个公式：

本文采用的实验平台为Matlab仿真平台，实验分别在原始图像和加密图像R分量的水平方向随机选取1000组相邻像素点，其像素点相关系数如表1所示。

从表1数据不难看出，原始图像的相邻像素点相关系数很高，而经过本文算法加密后的图像相邻像素的相关性变得很小，几近为0。

3.2 加密与解密

本实验中的原始图像为1 920×1 200的彩色图像“ 荷花.jpg”，令x₀= 0.22， y₀ = 0.13，z₀= 0.2，μ = 3.8。首先对原始图像进行加密，原始图像和加密图像效果如图3所示：

接下来，再进行解密，先试一下如果密钥记错能不能解密：假设此处将初始密钥改成x₀= 0.22， y₀= 0.13，z₀= 0.2，μ = 3.81，结果运行后根本无法解密，只有在输入与加密时一模一样的密钥才能解密图像，错误解密图像和正确解密后的图像效果如图4所示：

从上述实验结果可以看出，本文算法加密后的图像“面目全非”，根本无法辨认原始图像的样貌，隐蔽性较好，能够较好地保护该图像的信息；而由于混沌序列敏感的初始性，哪怕解密时初始密钥发生了一点点误差都无法正确地解密图像，所以密钥安全性较高；解密后的图像与原始图像从外观上看几乎没有什么差异，并且原始图像的直方图和解密后图像的直方图也几乎一模一样，如图5所示，由此可见该算法加密和解密可行。

3.3 抗缺损攻击测试

接下来，进行抗缺损攻击测试，将加密后的图像切去约三分之一的面积，考虑到画面主色调为绿色（Green） ，此处选择在G分量上筛检连续相同的像素值做标记进行优化，对比未作优化的解密算法和作了优化的解密算法的结果，可以看到明显的区别，受到缺损攻击的图像、未优化前的解密图像和优化后的解密图像分别如图6所示。

从图6可以看出，该加密图像遭受了较为严重的缺损攻击，极有可能丢失大量重要图像信息；因此如果用优化前的解密算法，解密后的图像质量比较差，有大量噪点，丢失了许多细节，如果此处传输的是重要的图片，就会造成一定的信息损失；而利用优化后的解密算法，解密后的图像基本重现了原始图像的各类细节，很好地保留了各类重要信息，证明优化后的算法大大提高了解密图像的还原度。

4 结论

本文设计了一种优化后的混沌置乱图像加密算法，通过对彩色图片RGB三个分量的置乱加密，并升级了原有的解密方法，通过Matlab仿真平台的实验验证获得以下结论：

1） 该算法的加密和解密算法原理类似，不复杂，比较容易实现。

2） 该算法完成后的图像相邻像素的相关性很低，说明加密效果好，隐秘性较好。

3） 由于混沌初始值敏感性特点，密钥必须一模一样才能解密，安全性较高。

4） 针对传输过程中加密图像受到较大面积的缺损攻击，提出了解密算法的优化方案，该方案原理简单，通过实验证明算法优化后的解密图像比没有优化算法直接解密的图像还原度确实高很多。