The factors that influence the electrochemical behavior of lithium metal anodes: electron transfer and Li-ion transport

ZHANG Meng-tian, QU Hao-tian, ZHOU Guang-min*

（Tsinghua-Berkeley Shenzhen Institute & Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China）

Abstract： Structured carbon-based hosts for the Li anode both improve the transport of Li-ions and reduce the electron transfer rate and have proven to be an effective way to suppress dendrite growth in lithium metal anodes. An in-depth understanding of these effects is needed to clarify the intrinsic electrochemical mechanism involved. We used the finite element method to simulate the two crucial processes controlling Li-ion behavior, electron transfer and Li-ion transport, and visualized the local deposition rate, the overpotential, and the Li-ion concentration in a three-dimensional (3D) Li//electrolyte//Li cell. Our analysis showed a competitive relationship between the rates of Li-ion transport and electron transfer. When the electron transfer rate is relatively slow, there are sufficient Li-ions available near the anode surface and the deposition behavior is controlled by electron transfer. However, when the number of Li-ions is low, Li-ion transport dominates the deposition process because it is unable to keep up with electron transfer, and this causes dendrite formation. Therefore, reducing the reactivity of the Li anode and accelerating Li-ion transport are the two key factors to produce uniform Li metal deposition on the anode, particularly under fast charging conditions and in practical use.

Key words: Lithium metal anodes；Finite element method；Electron transfer；Li-ion transport

1 Introduction

With the continued prevalence of electronic devices, the demand for higher energy storage density has been significantly increased, especially in the fields of rechargeable batteries and electric cars. The energy density of Li-ion batteries based on the graphite anode has almost reached the theoretical value following years of meticulous research and development[1]. To surpass this ceiling, Li metal with the highest theoretical capacity (3 860 mAh/g), low redox potential (−3.04 Vvsstandard hydrogen electrode), and low density (0.59 g/cm3) has been considered as the ideal anode material candidate for nextgeneration high-energy-density batteries[2–4], such as the Li-sulfur[5]and Li-oxygen batteries[6]. However,intrinsic issues like low coulombic efficiency, dendrite growth as well as safety concerns have still hindered Li anode practical application[3–4]. Naturally,due to the high chemical activity of Li metal and the limited Li-ion transport ability of electrolyte, it would inevitably cause uneven deposition and dendrite growth. The dendritic morphology leads to the creation of loose structures that easily collapse to form“dead” Li during the cycling process, lowering the coulombic efficiency[2,7].

Even worse, such dendritic growths pose a risk of piercing the separator and causing short circuit,which could lead to catastrophic thermal runaway[8]if not detected in time. Researchers have been attempting to regulate the deposition behaviors of Li-ions in order to resolve issues concerning the safety and coulombic efficiency of Li metal anodes for several decades. Li metal batteries (LMB) have shown good performance in coin cells. However, in practical pouch batteries or under fast charging conditions, the inherent problems of Li metal anodes are still difficult to overcome[9].

The challenge lies in the conflict between high electron transfer rates and sluggish Li-ion transport ability, thus, several techniques have been developed to tackle these 2 problems, including structured anode[10–11], electrolyte additives[12–14], functional sep-arators[15–16], anode surface modification[17–19]and artificial solid-electrolyte interphase (SEI)[20–21]. The structured anode such as carbon-based hosts tackle this challenge by accelerating Li-ion transport and reducing the electron transfer rate, thanks to their high surface for Li-ion deposition and improved Li-ion transport ability. This has promoted the advances in suppressing Li anode dendrite growth and boosting the coulombic efficiency[22–24]. However, corresponding theoretical models are still required to explain how these measures influence the intrinsic electrochemical behaviors of Li-ions. Several theoretical calculations based on the pseudo-two-dimensions (P2D)model[25–26]were conducted to simulate the Li-ion electrochemical behaviors in the LMB through the FEM, and they successfully visualized and predicted the Li-ion deposition process and anode morphology evolution[27–29]. However, these works generally simulate the influence of only a single variable on Li-ion deposition behaviors and hardly consider the combined effects of the basic processes of Li-ion transport ability and electron transfer rate.

Based on electrochemical principles, the process for Li-ion deposition can be divided into 2 distinct but mutually influencing steps[27,30–31]. The first step is the transport of Li-ions from the bulk solution to the electrolyte-electrode interface, followed by the release of electrons to reduce the Li-ions to Li-atoms. In general,in coin cell tests or at low charge/discharge rates,LMB usually exhibits good cycling stability and dendrite-free morphology, which could be interpreted by the fact that at small current densities, the speed of Liion transport and electron transfer could be self-consistent, i.e., there are adequate Li-ions at the interface of electrolyte-electrode to be reduced, and the electrochemical behavior of Li-ions is controlled by electron transfer. Nevertheless, at high-current densities during fast charging or practical applications, the limited transport properties of the electrolyte cannot match the speed of electrons being transferred from Li-ions to Li-atoms, therefore, the Li-ion deposition is Li-iontransport-controlled, causing a distinct Li-ion concentration gradient near the anode surface and leading to dendrite morphology[27]. Therefore, a deep understanding of the roles of Li-ion transfer and electrons transport in regulating the Li-ion electrochemical behaviors is imperative for Li anode protection.

Here, we present a quantitative analysis of the Li-ion diffusion coefficient and the electron transfer velocity which respectively contribute to the Li-ion transport and electron transfer ability to regulate the electrochemical behaviors. A 3D model to restore the real Li metal anode was established, in which the Nernst-Plank equation and Butler-Volmer equation[28,32–34] were solved by using the FEM based on the Comsol Mutiphysics software to visualize the local deposition rate, overpotential as well as the Li-ion concentration. Our work reveals the competitive relationship between Li-ion transport and electron transfer, and suggests that keeping the rate of Li-ion transport matched with the electron transfer could be beneficial to dendrite-free morphology and more stable Li metal anodes. Moreover, these results could serve as the criterion for Li metal anode protection and could be further used in other metal anode batteries.

2 Simulation sections

The FEM simulation was performed on the COMSOL Multiphysics 6.0 platform. Coupled with the tertiary current distribution module and deformed geometry module, the following are the main calculations of the governing equations.

The basic transport equations and kinetics equations have been illustrated above. Moreover, the behavior of Li-ions follows the mass conservation equation as well as the electrons conservation equation

where Niis the Li-ion flux, ciis the concentration, ziis the valence of each species in the electrolyte. And the boundary conditions near the substrate can be des cribed as:

wherenis the normal vector of the boundary.

The resulting deposition morphology was assumed to occur in the normal direction to the boundary with a velocityvn:

whereMandρis the molar mass and density of Li metal.

To simulate the morphology of Li deposits, we set the interface between the anode and electrolyte as a free boundary. The deposition thickness of Li was used as the displacement in the normal direction and can be expressed by:

In order to restore the rough surface of the real Li anode, we set a random distribution function at the electrode-electrolyte interface, the function is generated by[28]:

wherexandyare the spatial coordinates;mandnare the spatial frequencies;a(m,n) is the amplitude; and φ(m,n) is the phase angle. The amplitude is randomly generated by a Gaussian distribution function, and the phase angle and spatial frequency are derived from a uniform random distribution in a limited interval.

The electrolyte parameters we used were from LiPF6in EC∶DEC (1∶1), where the diffusion coefficientwas set as 2.69 e−10m2/s and thewas set as 100 A/m2. The stoichiometric coefficient of Li-ions in the electrolyte is set as −1, and the stoichiometric coefficient of Li-atoms on the electrode is set as 1.Both the anodic and cathodic electron transfer coefficients were set as 0.5, the temperature was fixed at 298 K and the initial Li-ion concentration was set as 1 mol/L. To make sure the precision of the calculation,the mesh quality is set as ultra fine.

3 Results and discussion

3.1 Basic electrochemical equations for Li-ion deposition behavior

As shown in Fig. 1a, in the charging process, Liions are transported from the bulk solution to the anode surface and then reduced to Li-atom, which mainly includes 2 major processes: electron transfer and ion transport, and it could be expressed by the simplified reaction[35]:

Fig. 1 (a) Schematic showing the Li-ion transport and electron transfer process with their corresponding controlling equations upon charging. The Li metal anode morphology under (b) electron transfer control with sufficient Li-ions and (c) Li-ion transport control with large Li-ion concentration gradient, the background color represents the concentration of Li-ions and the lines at the electrolyte-electrode interface show the local current densities

We can use the local current density at the electrolyte-electrode interface to directly reflect the kinetics of this reaction[28], which could be used to quantify the amount of Li-ion deposition. In general, achieving uniform Li deposition is equivalent to realizing uniform distribution of local current densities at the surface of Li anode, and the local current density (iloc)is affected by the overpotential of the anode surface that could be described by the famous Butler-Volmer equation:

whereRis ideal gas constant,Tis temperature in Kelvin,ηis overpotential, αaand αcare the anodic and cathodic charge transfer coefficients, respectively, andiexis exchange current density which is defined as the current density flowing equally in each direction at thereversible potential and can be used to characterize the ease of a reaction to occur[28,36], moreover, it is closely related to the electron transfer kinetics and the concentration gradient near the surface:

wherecLi+andcbis the concentration of Li-ion near the anode and in the bulk electrolyte, respectively,ieis the current density to represent the kinetics of electrons,vjis the stoichiometric coefficients,njis the number of electrons transferred, and the overpotential η above could be decided into concentration overpotential ηcand electrochemical overpotential ηe, which can be calculated from[37–38]:

where φsand φlare the solid phase and liquid phase potential, respectively,Ueqis the equilibrium potential of the reaction. Because of the large η in the Li metal anode, the Butler-Volmer equation could be simplified according to the above equations:

Such an equation includes both the Li-ion transport and the electron transfer, which manipulate local current densities by influencing the corresponding overpotential. Moreover, through this equation, electron transfer and Li-ion transport could jointly affect the local current distribution on the surface of the Li anode. Whereis a function related to the concentration gradient near the anode surface, therefore,the rate of the Li anode reaction could be divided into electron transfer partand ion transport part

The transport behaviors of Li-ions near the anode surface are described by the Nernst-Planck equation:

whereNLi+is Li-ion flux,DLi+,zis the diffusion coefficient and electrons of Li-ions andFis the Faraday’s constant.

Despite various equations and variables influencing the deposition, we could extract 2 extremely critical parameters, diffusion coefficient of Li-ionsDLi+[39]and the rate of electron transferie, in which they are the key factors corresponding to characterize the ability of ion transport and electron transfer process, respectively.

Fig. 1b c show the Li-ion deposition behaviors controlled by the electron transfer and Li-ion transport. In order to systematically quantify the effects of electron transfer and Li-ion transport in influencing the electrochemical behaviors of Li anodes, we established a 3D (40 μm×40 μm×20 μm) Li anode substrate model with a randomly distributed rough surface (Fig. S1) as the initial state to represent the real situation. Based on this model, the FEM simulation was performed using Comsol Multiphysics 6.0 platform to visualize the concentration field as well as electric field near the anode under different conditions.

3.2 Li-ion deposition behaviors under different applied current densities

The applied current density (iapp) is a critical parameter that has significant impact on the behavior of Li deposition[27]. On one hand, as theiappincreases,the thickness of deposited Li also increases, causing large volume expansion and stress concentration. On the other hand, according to the famous Sand’s time[40], the time for Li-ion depletion on the anode side is inversely proportional to the power of theiapp, and the dendrites grow easily once the Li-ions are depleted. Therefore, measurements ranging from 0.1 to 1 mA/cm2with the same capacity were conducted to investigate the impact ofiappon the Li-ion electrochemical behaviors. As shown in Fig. 2a, the morphology of deposited Li has minor differences when theiappincreased from 0.1 to 0.2 mA/cm2. However, when it is enlarged to 1 mA/cm2, the Li anode displays a significantly different morphology with obvious preferred deposition spots for Li-ions.

To better understand the phenomenon of different morphology on the anode surface, we calculatedthe ilocdistribution on the anode surface. Technically,the ilocreflects the local deposition rate which could be directly used to accurately reveal differences in Li-ion deposition morphology evolution[27,32]. Despite the different iappused in this simulation, the ratio of the ilocto the iapp(iloc/iapp) can be used to represent the relative current densities at the anode and characterize the probability for Li-ion deposition. From the simulation results in Fig. 2b, the relative current densities distribution is much more uniform under the lower iappfor 0.1 and 0.2 mA/cm2, which is also consistent with the morphology results. In contrast, under higher iappfor 1 mA/cm2, the Li-ion deposition probability distribution on the anode surface is totally different and quite uneven.

Subsequently, the Li-ion concentration distribution was calculated to further investigate the effect of different iapp. During charging, Li-ions are dissolved from the cathode, while being consumed and deposited at the anode, generating a concentration gradient in the electrolyte. After enhancing the iapp, the electron transfer rate could be greatly accelerated, i.e., the consumption of Li-ions at the anode side would be augmented, though the enlarged iappcould promote Liion migration, due to the limited Li-ion diffusion ability of electrolyte, the Li-ions cannot be supplemented in time to the electrolyte-electrode interface and the concentration gradient would be obviously enlarged.In accordance with Equation (5), the ratio of Li-ion concentration near the anode to the Li-ion concentration in the bulk electrolytecould contribute to the local current densities at anode surface and ultimately cause differences in morphology evolution.Additionally, the lower thethe greater the influence of Li-ion concentration on regulating the Li-ion deposition[39]. The Li-ion concentration gradient in Fig. 2c and S2 is slight under the iappof 0.1 mA/cm2and 0.2 mA/cm2, implying that the Li-ion transport factor would account little for the Li-ion deposition behaviors, whereas the Li-ion concentration gradient is tremendously enlarged when the iappis increased to 1 mA/cm2. Consequently, relative current densities differ significantly compared to those of the smaller iappof 0.1 and 0.2 mA/cm2.

Therefore, the increase in iappsimultaneously affects both the rate of electron transfer and the Li-ion transport, further influencing the local deposition probability. To explore the essential electrochemical behaviors specifically under the influence of high/low iapp, the surface distribution information of relative current density, overpotential and Li-ion concentration were compared to determine their relationship.We found that at small iapp, the deposition probability distribution of Li substrate would be much more uniform (Fig. 3a, d), and the similar phenomenon of homogenization also appears for the distribution of Liion concentration and the overpotential at the anode surface (Fig. 3b, c and S3).

Fig. 3 The relative current density distribution at the anode surface under the iapp of (a) 0.1 mA/cm2 and (d) 1 mA/cm2 with the same capacity(1 mAh/cm2), the overpotential distribution under the iapp of (b) 0.1 mA/cm2 and (e) 1 mA/cm2 as well as Li-ion concentration distribution under the iapp of (c) 0.1 mA/cm2 and (f) 1 mA/cm2. The scale bar in is10 μm. (g) Comparation for the distribution of relative current density and Li-ion concentration curves along the line at anode surface at the iapp of 1 mA/cm2

In addition to the uniform distribution, the intensity of the overpotential is also relatively smaller when the iappis changed from 1 (Fig. 3e) to 0.1 mA/cm2,which could be explained by the distribution patterns of Li-ion concentration at anode surface. Under the higher iapp, the Li-ions are consumed faster, leading to lower concentration, and display uneven distribution(Fig. 3f), which would lead to localin the direction perpendicular to the anode surface and enlarge the difference concentration distribution in the parallel direction, eventually resulting in the enhancement of concentration polarization and reflecting in the larger overpotential with uneven distribution. On the contrary, under the smalleriapp, there are abundant and uniform distributed Li-ions near the anode substrate.Under such conditions the overpotential for the Li-ion deposition is mainly from the polarization of electron transfer introduced by the rough anode surface. Besides, analyzing the anode surface information, we found that the regions with relatively fewer Li-ions perfectly correspond to the regions with larger local overpotential and higher deposition probability, especially at the higheriapp. This phenomenon could also be visualized by comparing the overpotential and concentration distribution curves (Fig. 3g) on the surface cross-section at theiappof 1 mAh/cm2. Along the selected curve (Fig. S4), the local shortage of Li-ions causes an enlargement in the concentration polarization and leads to an increase in the total overpotential,ultimately leading to a difference in local current density. These results also confirm the point that both,electron transfer and Li-ion transport modulate the corresponding overpotential to affect the electrochemical behavior of Li-ions according to Equation (5).

3.3 Li-ion deposition behaviors with different diffusion coefficients

We have demonstrated that at highiapp, the electrochemical behaviors of Li-ions are limited by Li-ion transport ability which results in large concentration polarization and dendrite growth, therefore, the Li-ion transport ability needs to be discussed further. Theoretically, the transport of Li-ions in the electrolyte is driven by migration triggered by electric fields and diffusion caused by concentration gradients, however,the migration rate is usually much faster than diffusion, thus the diffusion of Li-ions becomes the speeddetermining step[35]. As a result, the diffusion coefficientDLi+, which is directly related to the diffusion ability of Li-ions, becomes the key to studying the transport capacity of batteries. In general, theDLi+is determined by the physicochemical properties of the electrolyte, such as viscosity, density, Li-ion concentration and temperature[27]. The relationship between theDLi+with temperature and the Li-ion concentration is shown in Fig. S5, in which theDLi+is greatly affected by temperature, according to the Arrhenius equation. At low temperatures, the viscosity of the electrolyte increases and the diffusion coefficient decreases, resulting in easier dendrite growth, reduced coulomb efficiency, and limited fast charging performance[30].

Hence, we conducted the simulation for Li-ion electrochemical behaviors under differentDLi+gradients of 1 time, 5 times and 10 times (DLi+=M×D0Li+,M= 1, 5, 10) with theiappof 1 mAh/cm2. With the increase ofDLi+, the transport capacity of the electrolyte was effectively improved, and the Li-ion depletion has been mitigated with a much smoother Li-ion concentration gradient near the anode surface (Fig. 4a, S6).Due to the decrease of concentration gradient as well as the concentration polarization, the total reaction overpotential on the surface of the Li anode was also correspondingly reduced and more evenly distributed(Fig. 4b) according to Equation (5), which indicates the improved reaction kinetics of the Li anode and further leads to more uniform local electrochemical reaction. Fig. 4c demonstrates that even under a large current density, the homogeneous local current density distribution and uniform deposition morphology could still be achieved by improving the Li-ion transport capacity. The above results indicate the critical roles of improving the Li-ion transport capacity in realizing homogeneous deposition of Li anode.

Fig. 4 Li-ion electrochemical behaviors under different DLi+ gradients of 1 time, 5 times and 10 times (DLi+ =M× M = 1, 5, 10) with the iapp of 1 mAh/cm2. (a) Li-ion concentration distribution in the electrolyte.(b) Overpotential and (c) Relative current density distribution near the anode surface

3.4 Li-ion deposition behaviors under different electron transfer rate

In addition to the Li-ion transport factor, electron transfer rate was also taken into consideration.Herein, a set ofiewhich characterizes the electron transfer rate from 0.2 times to 5 times (ie=0.2, 1, 5) was designed to perform the simulation matched with different diffusion coefficientsM= 1, 10) under theiappof 1 mAh/cm2. As shown in Fig. 5a-b, different combinations of Li-ion transport ability and electron transfer rate present different distributed relative current density distribution.

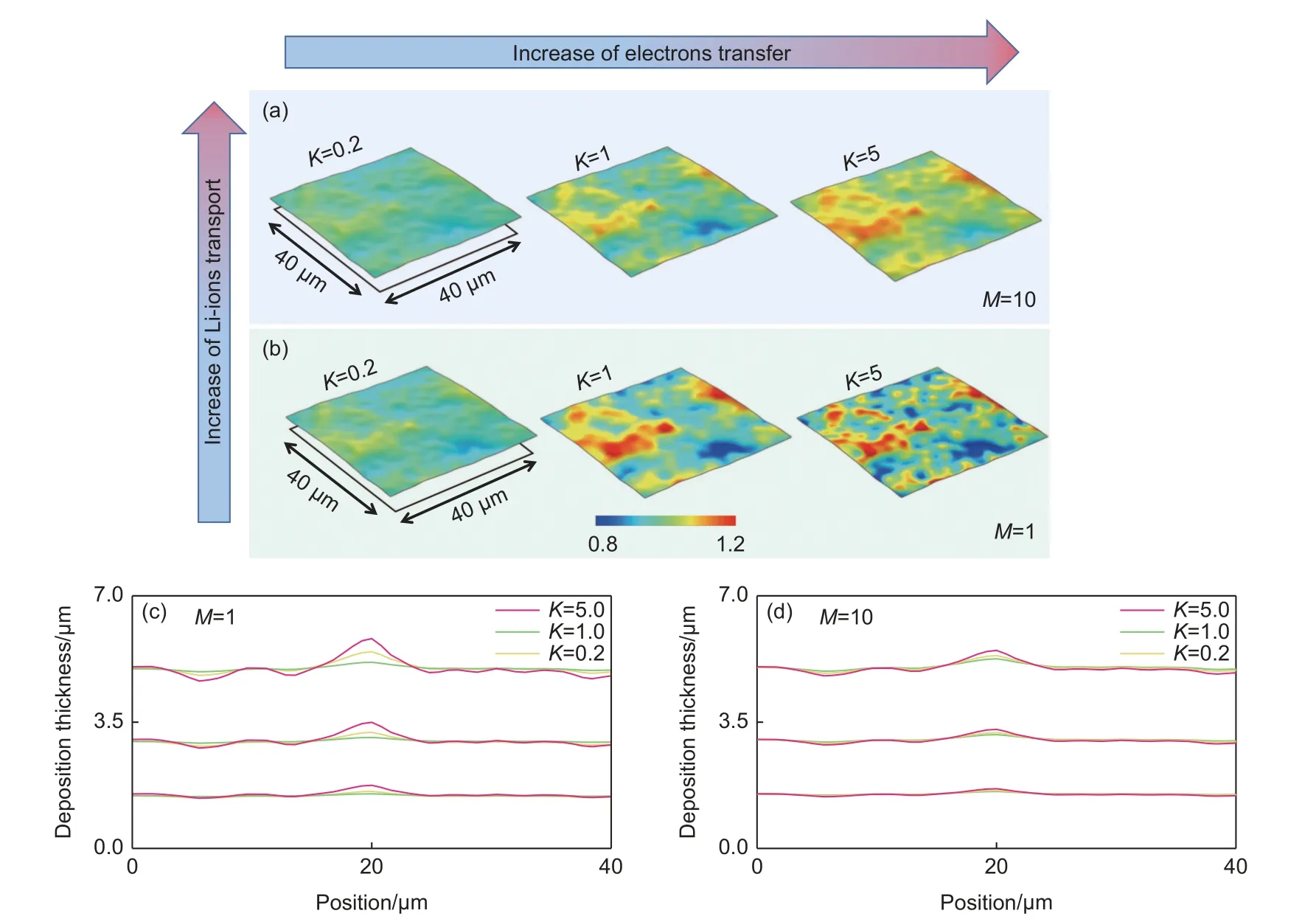
Fig. 5 Li-ion concentration distribution in the electrolyte under different electron transfer rate from 0.2 times to 5 times (ie=K× K = 0.2, 1, 5) matched with (a) high Li-ion coefficient (M = 10) and (b) low Li-ion coefficient (M = 1). (c) Distribution of Li-ion deposition morphology along the selected curve un- der different combinations of electron transfer rate and Li-ion coefficient

Specifically, in the case of lowie(K= 0.2), both of the high diffusion coefficient (M=10) and low diffusion coefficient (M=1) exhibit uniform reaction distribution, while at the highie(K= 5) condition, the relative current densities distribution of different Li-ion transport ability present totally different patterns. At a lower diffusion coefficient (M=1), as expected, the Liions have more preferred deposition sites, eventually resulting in the local dendrite growth (Fig. 5c-d). This is attributed to the fact that after the anode electron transfer rate increases, limited by the sluggish electrolyte transport properties, Li-ions could not be transported to the anode surface to be reduced to Li-atoms in time, leading to the anode reaction controlled by Liion transport. Therefore, when the anode electron transfer rate is relatively high, the diffusion coefficient must be synchronously improved, otherwise the dendrite morphology is difficult to avoid. Conversely,maintaining the diffusion coefficient at a higher level,even if the anode electron transfer rate is accelerated,the morphology of the could still remain relatively uniform. Hence, keeping the transport capacity of Liions matched to the electron transfer rate is crucial to achieving a more stable Li anode.

Based on the above conclusions, the Li-ion transport and electron transfer factors have synergistic effects modulating Li-ion deposition behaviors, which could be useful to better understand the Li anode protection work:

(1) Structured anodes, such as punching holes in graphene oxide hosts[10–11], carbon nanosheets[23]and porous carbon spheres[24], are effective way to promote a more stable Li anode. On the one hand, the porous structure could increase the surface area of Li deposition and effectively reduce the applied current density as well as the electron transfer. On the other hand, the vertical channels structure greatly shorten the actual path of Li-ion and promote the Li-ion transport.

(2) Organic and inorganic artificial SEI have also been extensively applied to achieve uniform Li-ion deposition. LiF has low Li-ion diffusion energy barrier and has been proven useful for facilitating the Liion transport[19], and other component such as Li3N has the chemical passivation ability to lower the Li anodes electron transfer rate[21].

(3) In terms of electrolyte additives, which could improve ionic conductivity by augmenting the type and number of conductive ions[14], or be helpful to form the robust SEI to accelerate Li-ion transport[13], it also plays a role from the perspective of improving Li-ion transport capacity.

Therefore, the current Li anode protection is basically carried out from the aspects of promoting Liion transport and reducing the electron transfer rate which could be interpreted by our simulation results.

4 Conclusion

Despite the volume of effort dedicated to the protection of Li anode for promoting LMBs from the aspect of accelerating Li-ion transport and slowing down the anode reaction rate, a comprehensive consideration for their joint influence has been lacking.Therefore, a 3D model representing the real Li anode was constructed to reveal their roles in controlling the Li-ion deposition behaviors based on FEM method.According to the Butler-Volmer equation, the Li-ion transport and electron transfer factors manipulate the Li-ion electrochemical behaviors by influencing their corresponding concentration polarization and electrochemical reaction polarization, respectively. The joint influence of parameters such as Li-ion diffusion coefficientDLi+and the rate of electron transferieunder differentiappwere simulated to quantify and visualize their impact on Li-ion electrochemical behaviors. Our findings suggest that matching the speed of Li-ion transport with electron transfer is the key to achieving uniform deposition of Li anodes. Failing to do so would lead to large concentration polarization and dendrite growth. Consequently, our work could deep-en the understanding of the electrochemical mechanism of Li metal anodes underlying the experimental phenomenon from the view of Li-ion transport and electron transfer, offering theoretical guidance for Li anode protection and facilitating the application of other metal anode batteries.

Data availability statement

The data that support the findings of this study are openly available in Science Data Bank at https://www.doi.org/10.57760/sciencedb.09394 or https://resolve.pid21.cn/31253.11.sciencedb.09394.

Acknowledgements

We appreciate the support from the National Key Research and Development Program of China(2019YFA0705703), Joint Funds of the National Natural Science Foundation of China (U21A20174), National Natural Science Foundation of China(52072205), Shenzhen Science and Technology Program (KQTD20210811090112002), Guangdong Innovative and Entrepreneurial Research Team Program (2021ZT09L197), Start-up Fund, and the Overseas Research Cooperation Fund of Tsinghua Shenzhen International Graduate School.

Author contributions

ZHANG M T and ZHOU G M conceived and designed the simu- lations. ZHANG M T performed the multiphysics simulations based on FEM and analysis the data. ZHANG M T, QU H T and ZHOU G M wrote the paper. All authors contributed to the review of the manuscript.

Competing interests

The authors declare no competing interests.