小题大做 深度探索

倪银萍

［摘 要］深度学习的特征就是“深”。深入解读教材，精准把握编者的编写意图，以便更有针对性地开展教学；深入研读学生，关注学生的兴趣爱好和思维特点；深入挖掘习题，由一题引发多题，促进学生对知识点的类化。

［关键词］习题；挖掘；深度学习

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）17-0034-04

深度学习是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。在这个过程中，学生掌握学科的核心知识，理解学习的过程，把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观，成为既具独立性、批判性、创造性，又有合作精神、基础扎实的优秀学习者，成为未来社会历史实践的主人。

习题是教学的重要资源，它不仅承载着练习巩固、拓展应用的功能，还是启迪思维、发展数学核心素养的重要载体。许多习题看似简单，实则有着丰富的思维含量，教师要深入钻研教材，深刻领悟编者的编写意图，有效开发和利用习题资源，从而让习题的价值得到最大化的发挥。

基于以上思考，笔者以三年级下册一道练习题为例，提出“小题大做、深度探索”的观点，从教材、学生、习题三个方面进行思考和探索，旨在根据教学目标和教材特点，重构习题，引导学生深入挖掘习题的价值，培养学生的深度学习能力。

一、解读教材——让深度学习纸上开花

学生要对概念形成深层次的理解。这里的理解不仅仅是字面上的知道、了解、明白之意，它更强调一种深层次的思考，即解释、思辨、推理、验证、应用等更难、更复杂和更具综合性的学习。

教师对教材理解的深度影响着课堂教学的深度，教师在设计练习题时必须深入研究教材，以求通联：了解知识的来龙去脉，明白每个知识点所要传递的思想方法以及情感态度，理解每道习题要培养学生怎样的能力。

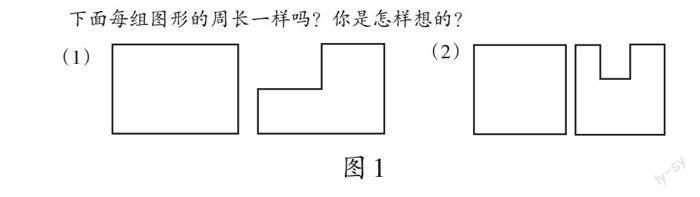
例如，周长是指封闭图形一周的长度。对此，教师要引导学生注意：不封闭的图形没有周长，封闭图形一周的长度不包括里面的线段，一周的长度包括线段和曲线和长度。这些也是学生容易出错的地方。教师要关注学生对知识的理解过程，预想学生容易出错的地方，在恰当的时间进行提醒。其实像图1这类从一个大图形中剪掉一个小图形的习题，在三年级上册“长方形和正方形的周长”课后练习中也曾出现过。

在图1这道练习题中，每组图形是以左右两个图形同时呈现，让学生比较左右两个图形的周长。这两组图都需要学生先描出两个图形的周长，在头脑中将这两个图形进行重叠，找出不同的部分，再根据长方形对边相等的特征去比较。图（1）中，因为两个图形刚好是长与长、宽与宽分别相等，所以两个图形的周长相等。图（2）中，因为右边的图形比左边的图形多了两条线段，所以两个图形的周长不相等。由此可见，这两幅图需要学生在空间想象的基础上实现图形的比较。

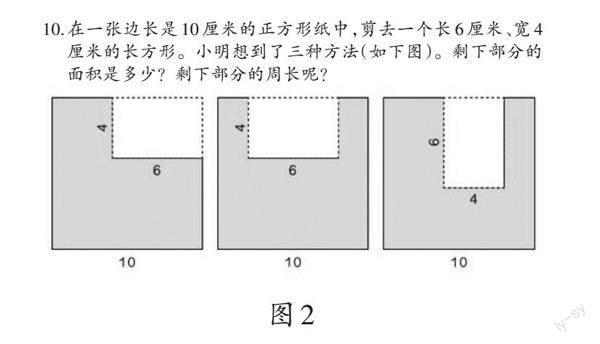
这道题与人教版教材三年级下册练习十五第10题（如图2）有异曲同工之处。可以看出，图2中，三个图形均是以虚线的形式表示被剪掉的部分，这有助于学生还原本来的正方形纸，以及看清楚被剪掉的小长方形的形状和特征。在这样的虚线图上，学生可以更清晰地找到相等的边，并通过平移的方式，发现第一个图形新增加的4和6两条边相当于被剪掉的两条边，刚好可以转化成一个完整的正方形的周长；第二个图形，6这条边平移上去后正好能够拼成一个正方形，只是还多两条4的边；第三个图形则是平移4这条边，拼成正方形，还多两条6的边。由此，求出这三个图形的周长。

二、研读学生——让深度学习深入人心

学生是学习的主体，学生的年龄特征、已有的知识基础、个性发展需求，是教学需要考虑的重要因素。要想真正读懂学生，就需要直面学生的学习现状，研究学生的实际学习需要。

1.关注学生兴趣

数学教学活动，特别是课堂教学应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维；要注重培养学生良好的数学学习习惯，使学生掌握合适的数学学习方法。

在多次解决同类问题之后，学生对问题的新鲜感会下降，分析问题的敏感度也会下降，甚至会形成思维定式，并把这种思维定式用在后面遇到的问题中，即使问题的条件有所改变，学生也无法进行正确思考。由此可见，在练习中，教师也要给学生设置一些问题性情境，让学生能跟着情境分析思考，保持思维的敏锐度，提高学生解决问题的兴趣。

2.关注学生思维

小学生的思维处于具体形象阶段，逻辑抽象思维和知识迁移能力不足。学生在学习周长后，明白封闭图形一周的长度叫作周长，了解了长方形和正方形周长的计算方法。在此基础上，教师应增加相应的变式练习，让学生在比较辨析的过程中深入思考，真正理解概念的本质，同时培养学生的知识迁移能力，提升抽象思维能力。

学生对一般图形的周长都能正确做出判断和计算，但是对一些不是长方形或正方形的图形的周长，比如像图2这类题，就会存在较多疑问。三年级学生对空间图形本质的理解和概念的掌握存在一定的困难，对图形的联想和想象能力较弱，阻碍了他们对实际问题的解决和空间观念的形成。

三、深挖习题——让深度学习落地生根

学生的数学学习内容应当是现实的、有意义的、富有挑战性的。数学的学习不能仅仅通过机械记忆与简单模仿来进行，教师要想培养学生深度学习数学的能力和习惯，深度教学必不可少。

数学学习的现实意义在于运用数学知识解决实际问题，因此，教师可以利用多样化的练习促进学生的深度学习，引发学生进行深层次思考，激发学生的探究欲望，让学生真正在理解中学习数学。

1.立足目标——活用教材

数学教学是以理解为基础的教学，教师要深入研究、思考教材和教法。同时，教师在制訂教学目标时除关注要求达成的知识目标外，还要注重能力目标的设定。

例如，像图2求不规则图形的周长这类问题，即便从三年级上册学到三年级下册，有的学生仍然不理解。笔者认为可能是学生对图形的周长认知不到位，也可能是学生不会运用长方形和正方形边的特征来解题。对此，笔者引导学生用笔描出这些变异图形完整的周长，将之与常规图形比较，看看是哪些地方变了，在变化处观察周长有没有变化。为了便于学生比较，教师可以把原来的图形画成方格图（如图3）。在方格图中，由于每个格子边长一样，此时再来观察原来的长方形或正方形就会发现，对应边相等的特征会更加明显。教师还可以给每一个方格标上序号（如图3），以便后续操作。

这样一个由12个小正方形组成的长方形，不管剪掉几个小正方形，比较剩下部分的周长都会更容易。

2.根据学情——整合教材

教师可以把如图3所示的方格图进行拆分，得到12个小正方形，让学生摆成其他图形，并思考：假设小正方形的边长为1，怎样摆周长最长？怎样摆周长最短？学生的摆法如下。

第一种摆法：长12宽1（如图4）

这个长方形的周长为（12+1）×2=26。

第二种摆法：长6宽2（如图5）

这个长方形的周长为（6+2）×2=16。

第三种摆法：长4宽3（如图6）

这个长方形的周长为（4+3）×2=14。

教材中也有类似的例题。例如，三年级上册教材第86页的例题：“用16张边长是1分米的正方形纸拼长方形和正方形。怎样拼才能使拼成的图形周长最短？”在最后的回顾与反思中，小精灵问：“只有这三种拼法吗？”

如果一定要拼成长方形或者正方形，根据16=16×1=8×2=4×4，确实只有三种拼法，但如果不要求拼成长方形或者正方形，就还可以拼出很多种组合图形。就像三年级上册教材第87页第4题：“把18幅绘画作品贴在一起，做一个‘绘画园地。要在‘绘画园地的四周贴上花边。每幅作品都是正方形，边长都是2分米。怎样设计‘绘画园地，才能使贴的花边最少？”这道题目没有像第86页的例题那样要求拼成长方形或者正方形，因此学生的思维能有很大的发散空间。

学生通常对长方形和正方形的周长掌握得较好，对不规则图形的周长掌握得不到位。那么，教师可以整合习题与例题，让学生用12个小正方形拼图形。除前面三种拼法外，学生其他拼法如下。

①周长不变

在第一种拼法（如图4）的基础上，从第一行拿1个小正方形放到第二行，图形周长没有变化，因为第12个小正方形之前是与第11个小正方形有1条边重合，现在是跟第1个小正方形有1条边重合。图4可以通过平移转化成比11×1的长方形多2条边的图形（如图7）。

周长为（11+1）×2+2=26。

②周长变短

如果再从第一行移1个小正方形到第二行，会发现，第二行的第2个小正方形与周围的2条边重合，比之前的拼法少了2条边。此时图形可以通过平移转化成比10×1的长方形多2条边的图形（如图8）。

周长为（10+1）×2+2=24。

如果将3个小正方形放到第二行，又会少2条边。以此类推，每从第一行移一个小正方形到第二行，周长都会少2，一直到两行的小正方形数量相等（如图9）。

如果第二行中的小正方形是分开不连续的，周长的变化情况就会更多（如图10），也更能锻炼学生对周长的分析思考能力。

教材是以静态的文本、图画将知识展现出来，而数学反映的是客观事物的发展变化规律，因此教师要采用各种手段来展现数学动态变化的过程，使学生感受其中的变化关系，从而达成教学目标。

3.适度延展——开发教材

教材只是课程资源的一部分，教师是课程资源的开发者，要想在课堂教学中真正体现以学生发展为本的教育理念， 就要对教材进行二次开发，创造性地使用教材。

（1）优化教材

教师在教学中重新整合教学内容，通过联系实际、化静为动、提炼总结等策略 ，更好地组织和引导学生进行学习活动；创设问题情境，留给学生一定的思维空间；改善学习方式，多为学生提供参与数学实践活动的机会。

例如，教师对图3这个方格图进行二次开发：“可以去掉最外圈的哪个小正方形，使周长不变？”引导学生从变化中发现不变。教师可以先去掉一个小正方形，引导学生发现：这个长方形最外圈一共有10个小正方形，如果去掉一个小正方形就一共有10种方法；在这10种方法中，周长不变的有4种（如图11），去掉的都是长方形四个角上的小正方形。

另外6種方法都会使周长变大，因为增加了2条边（如图12）。

学生仔细观察这些去掉的小正方形的位置，就会发现它们都不是长方形四个角上的小正方形，此时周长会增加2条边。

由此可见，如果接下来去掉的小正方形是前面4种类型之一，那么不管去掉几个，周长都不变；如果去掉的小正方形既有4种类型里的，又有6种类型里的，则图形周长的变化情况就比较复杂，要根据实际情况讨论；如果都是6种类型里的，那么图形的周长会变大。

（2）拓展教材

拓展延伸就是以教材习题为蓝本，分析习题的知识结构链，在学生的认知范围内，适度拓展习题的知识链，适度丰富习题内涵，合理拓展习题外延，有效发挥习题功能价值，拓宽学生的视野。教师要在深入钻研教材和研究习题的基础上，结合学情进行拓展创编。

例如，教师可以让学生从变化的图形中寻找不变的周长，或者从变化的图形中寻找变化的周长，也可以让学生探究“要使周长不变，最多可以去掉几个小正方形”的问题。这些都是学生感兴趣的内容，学生的探究欲望会被调动起来。“要使周长不变，最多可以去掉几个小正方形呢？”在这样富有挑战性的互动中，学生迫不及待地去寻找答案，最终他们可能会找到下面这些方法（如图13）。

一眼看去，剩下的小正方形似乎杂乱无章，但如果按照横行纵行的顺序依次来看，就会发现其实每一横行或者纵行都至少留下了一个小正方形，最后一个小正方形的作用在于连接边与边，所以最多可以去掉6个小正方形。在尝试操作的过程中，每操作一次就相当于算了一次组合图形的周长，这样经过多次的操作，学生就能加深对组合图形周长的理解，提高计算能力。

纵向拓展延伸，就是在纵深上对习题进行开发与设计，目的是将同一习题（或同一类习题）深挖，拓宽学生视野。一个好的问题可以持续地引发学生的思考，促使其对原有的知识进行重组构建，这样学生对知识的理解才会更深刻、更牢固。教师在平时的教学中积极对习题进行深加工和延伸拓展，并进行创造性的改编，衍生出一些新的问题和结论，将会大大提高教师理解和使用教材的能力，提升课堂教学的有效性，促进学生实现深度学习。期待深度学习可以从纸上开花到落地生根，再到开花结果，真正走入广大师生的心中。

［ 参 考 文 献 ］

[1] 郭华.深度学习及其意义[J].课程·教材·教法，2016，36（11）：25-32.

[2] 唐晓雄.浅析小学高年级数学习题资源的开发模式[J].黑河教育，2015（12）：41.

[3] 陈庆宪.怎样设计练习课的教学流程（二）[J].小学青年教师（数学版），2006（12）：22-23.

（责编 吴美玲）