基于深度机器视觉的稀土元素组分含量预测
张水平, 张奇涵, 王碧, 张小林, 蓝桥发, 郭浩然
(江西理工大学,a. 信息工程学院;b. 材料冶金化学学部,江西 赣州 341000)
稀土金属是航空航天、国防军工、节能环保等领域的关键战略资源,其应用在不同领域对提高产品质量、增强产品性能等方面[1]已表现出独特的优势。比如,高性能的钕铁硼永磁材料[2]被广泛应用于计算机、电视、核磁共振成像仪等高技术领域。但是,我国稀土萃取分离系统基本处于离线分析、手动调节和经验控制阶段,而稀土萃取过程中元素含量的快速检测有助于提高稀土产品质量。目前的检测方法多为分光光度法、光谱法、质谱法等,但是这些方法所用仪器存在检测延时长、有放射性、结构复杂和维护成本高等[3]问题,尚未得到普遍应用,且由于稀土萃取槽的强腐蚀环境[4]导致很难找出合适的传感器对稀土元素含量进行检测。因此,研究稀土萃取溶液中各元素含量的实时软测量方法具有重要意义。
目前,许多学者对稀土萃取生产中元素含量的软测量进行研究,文献[4-8]对稀土萃取组分含量进行软测量,通过将影响稀土元素含量的主要因素(如稀土料液流量、萃取剂流量、洗涤液流量和料液配分)作为辅助变量,对应元素含量作为主导变量,与传统机器学习算法结合建立模型,对稀土元素含量进行预测,预测结果符合实际生产标准。文献[9]探讨基于HSI 颜色空间描述的图像颜色特征分量一阶矩与组分含量的关系模型,实现对混合溶液中单一元素含量的检测。文献[10-13]利用稀土混合溶液图像在HSI 颜色空间下的特征分量H、S 一阶矩与稀土元素含量分别利用PAC-LSSVM、LSSVM、RBF 和GA-ELM 算法建立预测模型,实验结果精度符合生产检测标准。但是,上述方法均为离线建立的全局模型,在生产工况(如环境温度、稀土料液流量和萃取剂流量实时)变化时,不能有效预测组分含量。
为应对实时的生产环境,文献[14]针对上述问题对即时算法进行改进,提出一种基于模型更新策略即时学习算法的互信息加权最小二乘支持向量机(MISJITL-LSSVM)算法,将稀土萃取槽混合溶液图像的H、S、I 颜色特征分量一阶矩、相对红色分量RR 和颜色矢量角CVA 作为输入,Nd 元素含量作为输出,建立模型,在保证准确性的前提下提高模型的实时性。文献[15]结合主成分分析法提取稀土溶液图像在HSI和YUV 混合颜色空间下的时序特征,构造基于鲸鱼优化算法的最小二乘支持向量机分类器(WOALSSVM)对工况状态进行诊断,开发稀土萃取组分含量动态监测系统,满足稀土萃取组分含量检测的快速性和准确性要求。但是,上述方法均采用传统机器视觉技术,在100 个左右的小样本下进行建模,数据规模较小;且需要人工筛选并提取特征,过程较为繁琐。稀土元素含量软测量方法比较列于表1。

表1 稀土元素含量软测量方法比较Table 1 Comparsion of soft measurement methods for rare earth element content
近年来,深度学习用于分析各行业的数据[16]。其中,深度学习方法中卷积神经网络(Convolutional Neural Networks, CNN)的权值共享、池化操作和高位映射在图像处理方面表现突出,取得较多科研成果。本文引入CNN模型,从采集的1 210张稀土混合溶液图像中提取抽象表征;同时采用深度神经网络构建回归模型,用于预测元素组分含量。相较于传统方法,本方法数据规模提高了近12倍,且免去了人工筛选及提取特征的过程。多次重复实验表明,模型预测精度和时间成本均满足实时生产所需,具备泛化能力高、鲁棒性强的特点。对稀土萃取过程中元素含量实时在线检测有实际作用。
本文创新点包括:
1)引入CNN,根据CNN 模型结构建立轻量化VGG(Lightweight VGG)模型,从1 210 张Pr/Nd 稀土混合溶液原始图像中提取抽象表征,构建深度神经网络回归模型优化网络权值,用于稀土元素含量预测,模型泛化力更强。
2)提出相对误差评价机制,考虑到稀土元素含量软测量的误差评价指标为相对误差,在验证集样本预测值与真实值之间的相对误差绝对值下降时自动更新并保存网络权值,提升模型预测精度。
1 数据集的制备
为实现稀土混合溶液图像的采集,实验所使用的Pr/Nd混合溶液由如下途径获得:
1)原溶液组分含量测量:于赣南某稀土公司分别购买纯度均为99.9%的1 L 1.827 5 mol/L PrCl3和1 L 2.063 mol/L NdCl3萃取溶液,其稀土浓度和配分均由国家钨与稀土产品质量监督检验中心提供。
2)溶液稀释:将2 种原溶液的浓度分别稀释为0.01~0.50 mol/L 各11 种不同浓度且透光性良好的溶液。
3)溶液混合:将2种不同浓度Pr和Nd溶液各50 mL相互混合,共得到121 组不同浓度的Pr/Nd 混合溶液,其中,混合溶液中各元素浓度为原浓度的1/2。
由上述步骤得到Pr/Nd 含量在1.96%~98.04%之间的多组混合溶液,将各稀土混合溶液倒入收集皿中密封保存。实验制备的稀土混合溶液对光线呈现一定反射性和折射性,透光性较好,满足基于机器视觉实验测量稀土元素含量的光学成像条件。同时,在充满稀土混合溶液的容器中形成了“离子颜色特征带”(表2),为快速、准确且可连续检测的图像识别技术的使用提供可行途径。
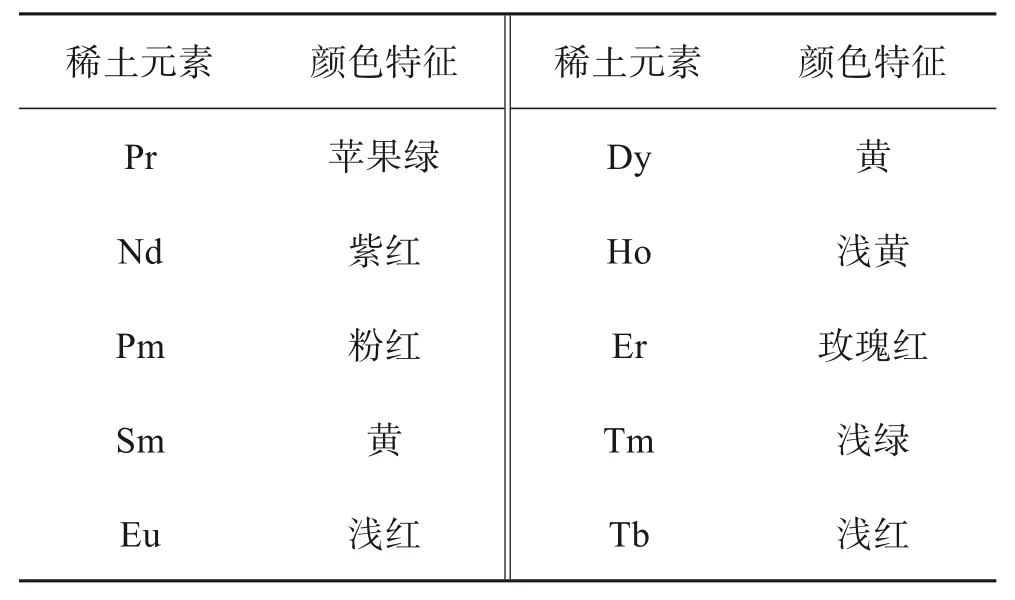
表2 部分稀土离子的颜色特征Table 2 Color characteristics of rare earth ions
实验图像采集时,将稀土元素混合溶液倒入长×宽×高为150 mm×5 mm ×170 mm 的石英容器中,直至溶液填充满容器。随后将容器置于60 cm 摄影棚中。其中,摄影棚中搭建两处LED光源,光源输出电压为24 V、功率为48 W、灯珠流明最大为15 000 lm;背景为纯白色;图像采集设备为NIKON D700 相机;最终采集图像为4 256×2 832 分辨率的JPG 格式图片。由于拍摄得到的Pr/Nd混合溶液图像(图1)中包含石英容器边缘外非溶液部分及边缘内颜色不均匀部分,因此将拍摄图像中充满颜色特征的部分进行裁剪,每组溶液图像依照从上至下、从左至右的顺序裁剪10张图片,共获取1 210张颜色均匀的稀土混合溶液图像。将混合溶液图像按照不同的Pr 含量归为79个类别,并将每个类别标记上Pr含量真实值,制备成完整数据集,用于构建模型。

图1 部分不同组分含量Pr/Nd混合溶液图像:(a) 98.04% Pr, 1.96% Nd;(b) 42.86% Pr, 57.14% Nd;(c) 33.33% Pr, 66.67%, Nd;(d) 2.17% Pr, 97.83% NdFig.1 Images of Pr/Nd mixed solutions with different component contents:(a) 98.04% Pr, 1.96% Nd;(b) 42.86% Pr, 57.14% Nd;(c) 33.33% Pr, 66.67%,Nd;(d) 2.17% Pr, 97.83% Nd
2 CNN结构
为提高网络的学习能力,CNN 利用图像的空间相关性提取图像轮廓信息,有效地从大量样本中学习相应的特征,避免复杂的特征提取或构建过程。CNN 可直接输入三维图像,通过非线性变换从原始图像中提取更加抽象的表征,提高模型的泛化能力。并且在整个过程中只需少量的人工参与。CNN 包括:输入层、卷积层、池化层、全连接层及输出层。
2.1 输入层
输入层用于样本的输入。如输入一张大小为224×224×3 的彩色图像,输入层能读取到224×224 的矩阵,3为深度(即R、G、B)。
2.2 卷积层
卷积层[17]包含多个特征面,每个特征面包含多个神经元。下一层特征面的每个神经元通过卷积核(一个权值矩阵)与上一层特征面的局部区域相连接,其中每个神经元的输出值由该局部区域的加权和连接的激励函数(如ReLU 函数)获得。上一层特征面的局部区域与对应相连的下层特征面权值共享,结构如图2 所示。每1 个卷积层的每个输出特征面的大小oMapN计算如式(1)所示:

图2 卷积层与池化层一维结构示意Fig.2 Schematic diagram of one-dimensional structure of convolutional and pooling layers
式(1)中:W为输入特征面大小;F为卷积核大小;P称为Padding(若为1则在特征面四周补零,使卷积过程充分提取特征面边缘数据);S为卷积核在上一层特征面局部区域的滑动步长。在图2 中,设置F为1×3,P为0,S为1。ReLU 函数的计算公式如式(2)所示:
2.3 池化层
池化层[17]连接在卷积层之后,包含多个特征面。池化操作不会改变特征面的个数,而是对特征面进行下采样操作,减小下一层特征面的大小,同时使模型能够抽取更广泛的特征,每个特征面唯一对应于上一层的一个特征面,结构如图2 所示。其中,最常用的池化方法为最大池化(即取特征面局部域中值最大的点)。每个输出特征面的大小DoMapN计算如式(3)所示:
式(3)中:oMapN为输入特征面的大小,N为池化核大小。在图2中,N为2。通过池化操作使得神经元数量减少,降低网络模型的计算量,避免过拟合,提高模型的泛化能力。
2.4 全连接层及输出层
在经多个卷积层和池化层后,连接全连接层[17]。全连接层将其中每个神经元与前一层的所有神经元进行高维映射,用于整合卷积与池化层中综合提取的特征信息,一般采用ReLU 激励函数提升模型整体性能,结构如图3 所示。全连接层可为1 个或1 个以上,最后一层的输出值一般采用Softmax函数传递给输出层。Softmax函数的计算如式(4)所示:
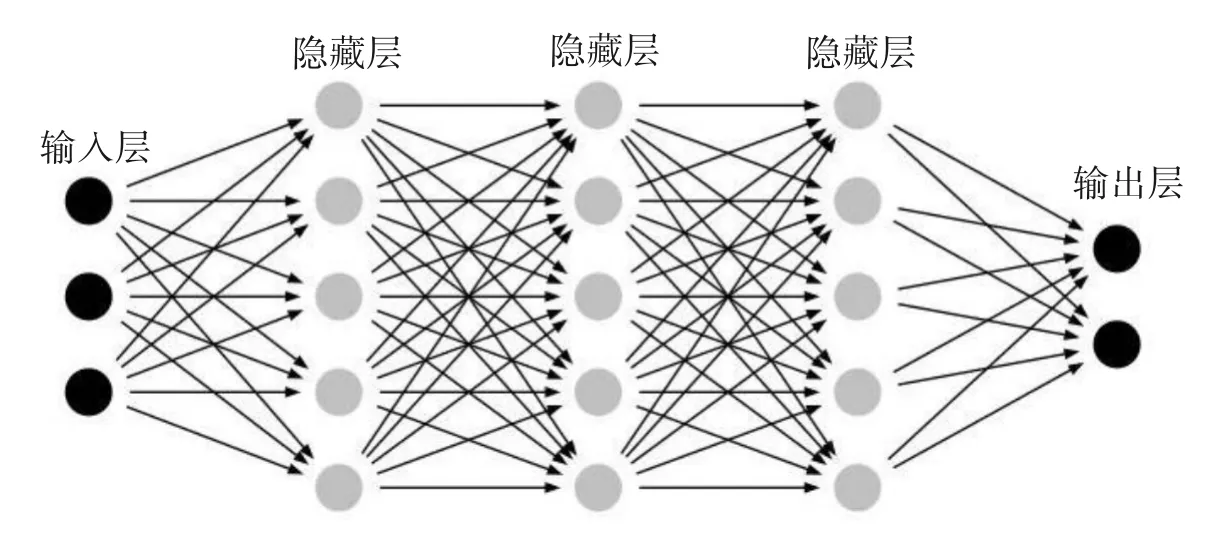
图3 全连接结构示意Fig.3 Schematic diagram of fully connected structure
式(4)中:C为输出节点的个数(即分类的类别个数),Zi为C中第i个节点的输出值。通过Softmax 函数将多个类别的输出值转换为范围在[0,1],和为1的概率分布。
通常采用Dropout 技术,设置Dropout 值为0.5,使全连接层隐藏层神经元的输出值以1/2 的概率变为0,使部分隐藏层节点失效,避免模型训练中的过拟合现象。由于Dropout技术的随机性,降低了神经元之间相互适应的复杂性,使整体网络更具备鲁棒性,目前CNN 模型基本采用ReLU+Dropout[18]技术,并取得很好的性能。图3中,神经元间的连接和前向传播的方向采用箭头线段表示,隐藏层和输出层中每个神经元的输入值为上一层所有神经元的输出与连接权值的加权和。设定是全连接层中第l层第m个神经元的输入值和分别为该神经元输出值和偏置值,为该神经元与第l- 1层第i个神经元的连接权值,则有式(5)、式(6)。
当全连接操作用于分类任务时,输入矩阵的维度为输入神经元个数,分类任务类别数为输出神经元个数。全连接操作可以分为前向传播和后向传播两个阶段,后向传播开始于全连接层的输出层,设定第l层为输出层,yj为输出层第j个神经元的输出值,tj为输出层第j个神经元的期望输出值,将两者建立损失函数,设损失函数如式(7):
对式(7)求一阶偏导,并使用梯度下降法[19]在损失值更低时更新网络权值,则网络权值更新公式如式(8),其中η为学习率。
3 模型构建及训练
3.1 轻量化VGG模型
CNN模型中通过卷积层提取各种不同的局部特征,池化层减少所提取局部特征神经元个数,降低复杂度,增强模型的鲁棒性。将所提取的特征综合起来反馈到全连接层进行正向传播和反向传播,利用梯度下降法自动更新网络权值。同时使用ReLU+Dropout 技术随机使神经元失活,使整体网络更具有鲁棒性和泛化能力,以获取最优网络权值。根据卷积层、池化层、全连接的组合不同,衍生出许多经典CNN 模型,包括LeNet、AlexNet、VGGNet、ResNet等,网络模型根据项目的样本数据集实际情况选择。由于VGG(Visual Geometry Group)模型是从图像中提取CNN 特征的首选方法,按照卷积操作次数的不同可划分为VGG11、VGG13、VGG16 等基本模型结构(图4)。
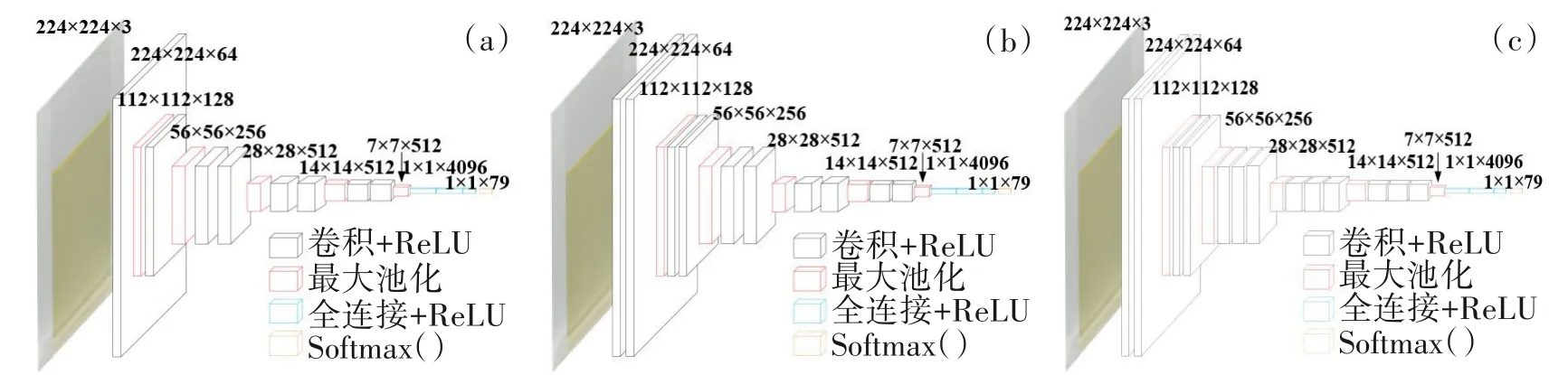
图4 部分VGG基本模型结构:(a) VGG11;(b) VGG13;(c) VGG16Fig.4 Part of VGG basic model structure:(a) VGG11;(b) VGG13;(c) VGG16
本文所采集数据集相对不大、图像特征也不复杂,因此选用卷积和池化操作相对更少的VGG11 模型,减少卷积操作的次数、卷积核和全连接层节点的个数,建立轻量化VGG模型,结构如图5所示。
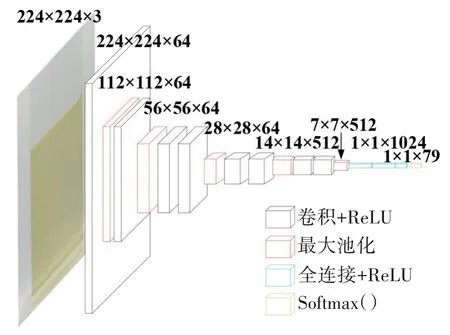
图5 轻量化VGG模型Fig.5 Lightweight VGG model
输入大小为224×224×3 的稀土混合溶液图像,输入层能读取到224×224 的矩阵,3 为深度(即R、G、B),并将图像标记上对应不同元素含量的真实值,输入模型进行训练。模型共有5 组卷积和池化迭代操作过程,之后通过后向传播使用梯度下降法不断更新权重参数,直到寻找到最佳的网络权值。
池化层通过不断减小特征面大小,减少神经元的数量,降低计算量,在一定程度上避免了过拟合。经上述操作后,起始大小为 224×224×3 的图像缩小为7×7×512 的数字矩阵。通过三层全连接,其中第一、二层全连接隐藏节点数为1 024,第三层全连接的隐藏节点数为79,将数字矩阵展开为一个表示类别的列向量,最后通过Softmax 函数输出稀土混合溶液图像中各组分含量的概率值(1×79)。
3.2 优化网络权值
VGG 模型一般用于分类任务,而预测稀土元素含量为回归任务。因此,为获取准确单一稀土元素含量的预测值,本文将轻量化VGG 模型Softmax 函数输出的概率值列向量(1×79)与对应元素组分含量的真实值行向量(79×1)作内积,输出稀土混合溶液图像中的元素含量预测值,与对应稀土混合溶液的元素含量真实值通过损失函数构建深度神经网络回归模型,对网络权值进行优化,用于模型的预测。损失函数用于衡量实际变量值和预测值之间的差异,损失值越小说明预测越准确,因此选择合适的损失函数较为重要。下面探讨回归模型中使用的损失函数问题:
1)回归模型中通常采用的损失函数有L1Loss和L2Loss,分别用于计算平均绝对误差MAE(式(9))和均方误差MSE(式(10)):
式(9)、式(10)中:i(i∈n)为第i个待测样本,yi为模型预测值,ŷi为待测样本对应的真实标签值,n为所预测样本总个数.
2)由式(9)、式(10)可知,相较于L1Loss,L2Loss将误差平方化,会加剧忽略微小的误差。例如,真实元素组分含量为0.001的溶液,其预测值为0.011。虽然误差是真实值的10 倍,但数值较小。若使用L2Loss,会进一步增加修改该误差的难度。
3)L1Loss 用于求最小绝对值偏差,能处理数据中的异常值,因而更具鲁棒性。相较L2Loss,L1Loss具有较为稳定的解。
因此,本文采用L1Loss作为模型的损失函数,用于构建深度神经网络回归模型。将采集的数据集进行分割,其中,80%作为训练集,10%作为验证集,10%作为预测集。本文以计算Pr 元素含量为例,将训练集和验证集标记对应Pr 元素含量的真实值,并将训练集输入模型用于训练。设定模型输入训练集的稀土混合溶液样本批大小(Batch)为n,ŷi为输入样本对应的Pr 元素含量的真实值,yi为输入样本通过模型输出的预测值,ŷi与yi同维度,则按照式(9)计算该批次数据样本的损失值,在正向和反向传播迭代过程中利用梯度下降法(式(8))自动优化网络权值。
同时,利用优化器使初始值为1×10-4的学习率自适应地改变,损失函数在合适的学习率下能够在合适的时间收敛到局部最小值。实验采用的优化器为RMSprop。
该优化器能解决某些迭代梯度过大而导致自适应梯度无法改变的问题,加快神经网络的收敛。
为更好地体现稀土萃取流程中组分含量软测量的可信程度,将相对误差作为评价指标,而3.1 节中介绍的深度神经网络回归模型计算的是训练集样本预测值与真实值之间的绝对误差。因此,本文提出相对误差评价机制,在模型每次迭代训练过程中的梯度不再下降时,通过式(11)计算验证集样本预测值与对应Pr 含量真实值之间的相对误差绝对值(RE),并在误差值降低时自动更新与保存网络权值。为便于后续对比实验,按照式(12)计算绝对误差评价机制下验证集样本预测值与对应Pr含量真实值之间的绝对误差绝对值(AE),并保存对应网络权值。
式(11)、式(12)中:i(i∈n)为第i个待测样本,yi为模型预测值,ŷi为待测样本对应的真实标签值。
3.3 训练过程及预测
采用为Windows10 操作系统,CPU Intel Core i7-12700F(12 核),GPU RTX3080(内存为10 GB),代码实现统一采用PyTorch 深度学习框架。深度神经网络回归模型构建后,进行迭代训练,由图6 可见模型训练过程中训练集损失函数值在迭代至近第300 次时趋于收敛,从而完成模型的训练部分。由回归模型中得到最优网络权值,在预测板块加载权值文件,进行预测集的预测,得到Pr元素含量的预测值后,按照式(13)求出对应Nd元素含量的预测值:
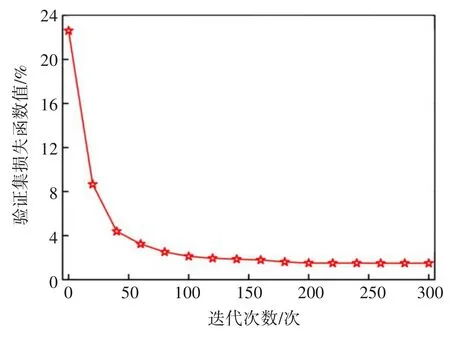
图6 模型训练中验证集损失值随迭代次数变化过程Fig.6 Variation of the loss value of the validation set with the number of iterations in model training
4 实验与分析
4.1 验证性实验
为验证相对误差评价机制在以相对误差为评价指标的稀土元素含量软测量过程的有效性,将本文所提方法(轻量化VGG 模型)分别在相对误差评价机制与绝对误差评价机制下保存的网络权值对测试集20 个样本进行Pr 元素含量预测,并将预测值与样本对应真实值按照式(11)计算相对误差绝对值(RE)用于衡量两种机制的性能。实验对比结果见图7。
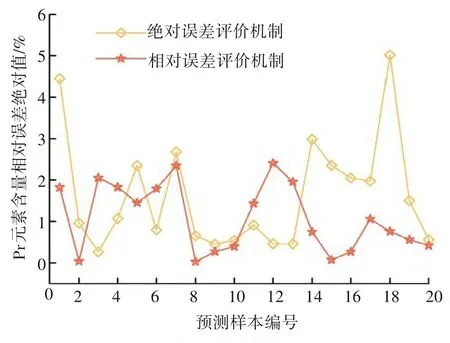
图7 不同评价指标机制在20个测试集样本中的相对误差绝对值Fig.7 Relative error absolute value of different evaluation index mechanisms in 20 test set samples
由图7 可以明显看出,预测集20 个样本中,相对误差评价机制下的Pr元素含量相对误差绝对值普遍比绝对误差评价机制下的低且波动范围小,最大相对误差绝对值在3%以内。而绝对误差评价机制下有一个样本的Pr元素含量相对误差高于5%,不满足稀土萃取分离过程中对元素含量检测最大相对误差在±5%[20]范围内的最低要求。因此,相对误差评价机制更适用于以相对误差为评价指标的稀土元素含量软测量。
4.2 对比实验
为体现本文所提轻量化VGG 模型对稀土元素含量预测的优越性,将本方法与多层感知机(Multilayer Perceptron,MLP)、VGG11、VGG13 和VGG16进行对比,为保证对比实验的公平性,上述模型都通过L1Loss 损失函数构建回归模型并进行训练,在相对误差机制下保存网络权值,并设置统一的全连接层节点个数与模型主要参数(表3),这些参数是提升模型性能的一般参数。因此,这对上述模型都是公平的。

表3 主要参数设置Table 3 Main parameter settings
此外,将传统机器视觉方法中常用的最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)在本文所采集数据规模下进行训练及预测,并与本文方法进行对比。
对比实验如下:
1)为体现VGG 模型中卷积、池化操作捕捉稀土混合溶液图像抽象表征的有效性,将轻量化VGG 模型除去卷积、池化操作后的3个全连接层构建多层感知机,保留ReLU+dropout 操作,建立稀土元素组分含量预测模型。
2)采用VGG 模型中常用的VGG11、VGG13 和VGG16建立稀土元素组分含量预测模型。
3)将本文采集数据集中的训练集与预测集待测样本从RGB 颜色空间转换到HSI 颜色空间,提取每张图片的H、S 特征分量一阶矩,用于构建基于LSSVM的稀土元素组分含量预测模型。
4)采用测试集中20 个不同Pr 元素组分含量的稀土混合溶液图像样本对本文方法与上述所有方法进行测试,将预测值与对应样本真实值分别按照式(14)、式(11)和式(15)所示的平均相对误差(MRE)、相对误差绝对值(RE)、和均方根误差(RMSE)公式进行计算,可得到如图8 所示的相对误差绝对值对比图,如表4 所列的MRE、最大相对误差绝对值(REmax)和RMSE测试性能指标值。
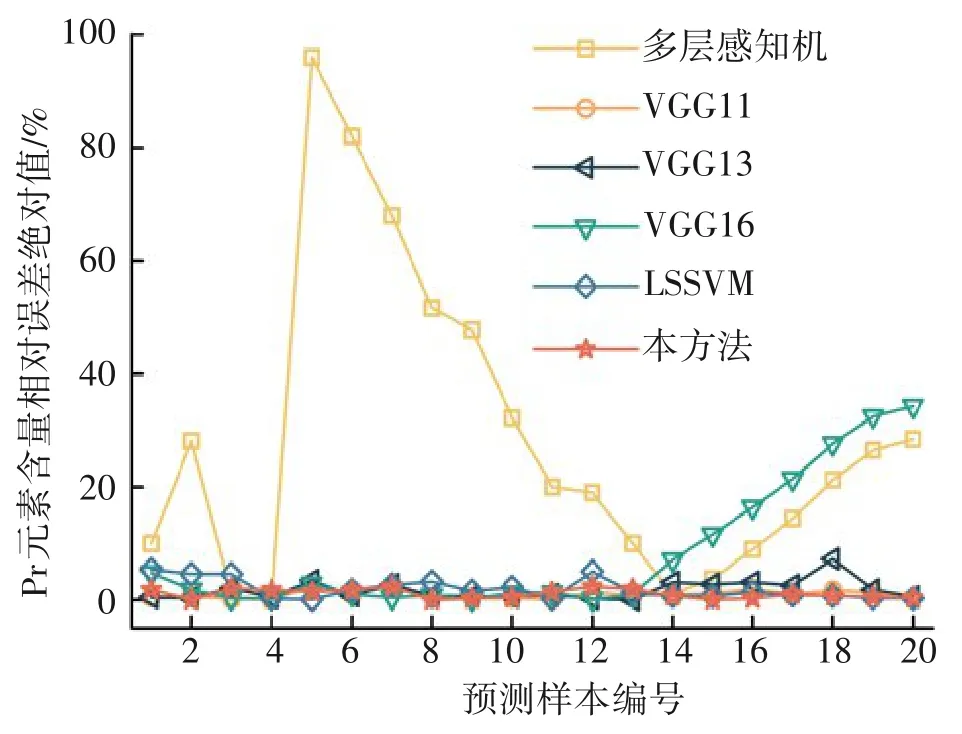
图8 6种模型测试时Pr元素含量的相对误差绝对值Fig.8 Absolute value of relative error of Pr element content in 6 models test
式(16)、式(17)中:i(i∈n)为第i个待测样本,yi为模型预测值,ŷi为待测样本对应的真实标签值,n为所预测样本总个数。
由图8和表4可以看出:
1)多层感知机各项性能指标的误差值远高于其他VGG 模型,说明一般的全连接神经网络无法有效捕捉到稀土混合溶液图像中的特征,而VGG 模型中的卷积和池化等操作能充分捕捉到稀土混合溶液图像中的内部差异。
2)比较VGG11、VGG13 和VGG16 3 种模型对稀土元素含量预测的测试结果,可知,VGG11 模型的3 个测试性能指标值MRE、MAXRE和RMSE远优于其他2个模型,说明卷积和池化操作相对更少的VGG模型更适合稀土混合溶液图像中的元素含量预测。
3)本方法是基于VGG11 模型进行的改进,减少了卷积操作次数、卷积核和全连接层节点的个数。将本方法与VGG11 模型进行比较可以发现,前者的最大相对误差及均方根误差更低,说明本方法能在一定程度上提升模型预测的精度和稳定性,并减少了计算量,更适用于稀土元素含量预测。
4)将本方法与LSSVM 进行比较,本方法MRE下降了0.981 1%、MAXRE下降了3.010 3%、RMSE下降了0.004 0,各项性能指标都优于LSSVM,且LSSVM最大相对误差绝对值高于5%,超出了稀土萃取分离中元素含量检测最大相对误差的要求范围。
在本文所采集数据集规模下,采用LSSVM 对稀土元素含量进行预测,精度不及本方法,且本方法免去了人工筛选和提取图像特征的复杂过程。
为验证本方法对稀土元素含量预测的准确性与稳定性,采用十折交叉验证法将数据集分成10 份,轮流将其中9 份作为训练数据,1 份作为测试数据(其中,验证集与预测集各占50%),循环进行10 组实验。将每组测试样本的Pr元素含量的预测值与真实值分别按照式(14)、式(11)和式(15)式计算得到平均相对误差(MRE)、最大相对误差绝对值(REmax)、和均方根误差(RMSE)如表5 所列,以衡量模型性能。
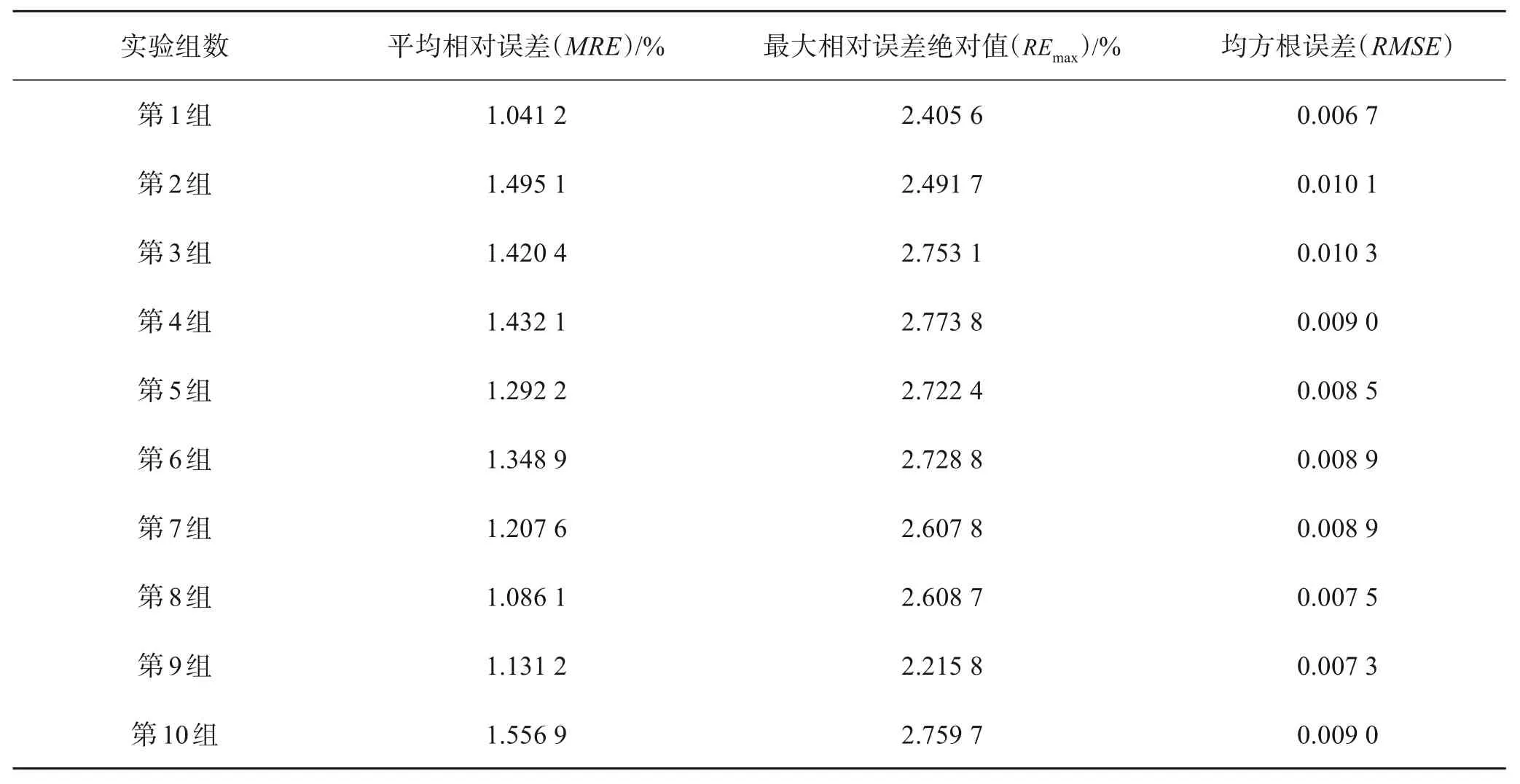
表5 十折交叉验证法每组的性能指标值Table 5 Performance index values for each group of the ten-fold cross-validation method
由表5可得10组中最大平均相对误差为1.556 9%、最大相对误差绝对值为2.773 8%、最大均方根误差为0.010 3。说明模型整体精度和稳定性都较高,满足稀土萃取分离过程中元素含量检测最大相对误差在±5%范围内的要求,而单个样本的预测耗时少于2.8 s,预测时间成本满足稀土萃取生产实时检测的要求。
5 结 论
针对稀土萃取的复杂性和结果多样性导致对稀土元素含量的分析难度比较高,人工进行稀土元素含量预测费时费力,且需要使用昂贵且并不高效的仪器装置,存在检测延时大、有放射性、结构复杂和维护成本高等问题。本文根据深度学习方法中CNN模型结构,建立轻量化VGG 模型,同时采用L1Loss损失函数构建深度神经网络回归模型,提出相对误差评价指标在验证集预测值与真实值之间相对误差绝对值下降时保存网络权值,用于稀土混合溶液图像中的元素含量预测。经多组实验得出以下结论:
1)本文所提轻量化VGG 模型能充分捕捉具备离子颜色特征的稀土混合溶液图像抽象表征,相对误差评价机制能有效降低测试样本预测值与真实值之间的相对误差。
2)对比实验中表明,在本文采集数据规模上,本方法对稀土元素含量预测精度高于传统机器视觉方法,此外,本文法免去了繁琐的人工筛选及提取特征的过程,减少了人工开支。
3)十折交叉法证明本方法对稀土元素含量预测稳定性高、泛化力强,最大相对误差为2.773 8%,满足稀土萃取分离过程中对元素组分含量检测最大相对误差在±5%范围内的要求。单个样本预测耗时少于2.8 s,时间成本满足实际萃取生产中对组分含量检测所需,在稀土萃取生产方面是有意义的。

