经历数学发现过程 建构有效数学课堂

陆颖

［摘  要］ 在数学教学中，教师可以引导学生切实体验发现、探究、验证、建构、再发现、再探究、再验证、再建构的完整过程，这样的探究经历可以促进有效数学课堂的建构。研究者以“钉子板上的多边形”专题活动课为例，提出以动手操作为载体，提升专题活动的有效性；以探究性问题为驱动，彰显数学探究的思维性；以循序渐进的活动设计为指引，体现数学发现的递进性。

［关键词］ 数学发现；动手操作；问题；建构

一、问题的提出

数学发展史的进程中，数学家们发现任何一个定理或公式都需要经历一个很长的过程，不仅需要在不完全归纳法后以大量事实进行验证，还需要利用严格的数学证明来确认其正确性。倘若在数学教学中，教师可以引导学生像科学家一样经历发现和验证的过程，切实体验发现、探究、验证、建构、再发现、再探究、再验证、再建构的完整过程，想必这样的探究经历对学生而言会印象深刻，更是弥足珍贵的。

教材中“钉子板上的多边形”是一节专题活动课，这一内容主要是为了让学生通过数学探究获得新的发现。教学时教师要通过合理利用教材，结合具体的学情进行斟酌，给予学生经历一次完整的数学发现的真实体验，实现智慧的碰撞。基于以上思考，笔者与教研组的同事进行商讨，经历了2次教学尝试，以进行有效数学课堂的建构。

二、教学尝试与思考

（一）初次尝试

1. 初步感知，发现规律

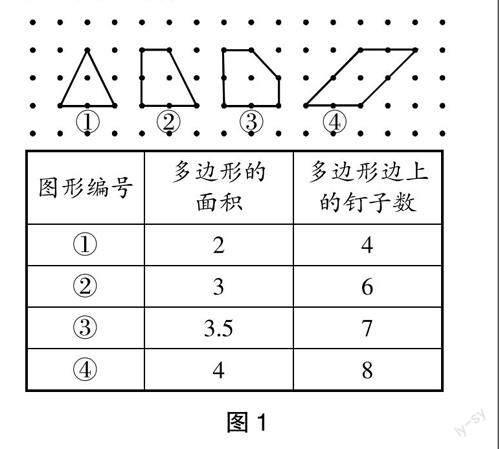
问题：如图1，请观察图形，并独立填写表格。

师：经过刚才的独立思考，你们一定有了自己的想法和认识，下面分小组讨论从表格中能发现什么？（学生展开了热烈讨论，思维不断碰撞，很快有了统一的想法）

生：多边形的面积即为多边形边上的钉子数的一半。

师：非常好。如果用字母b表示钉子数，S表示多边形的面积，可以得出什么公式？

生：S=b÷2。（教师板书）

师：观察了表格，我们再来仔细观察这组图形，你能发现它有什么特征？（学生仔细观察）

生：在图形的内部都仅有1颗钉子。

师：真是观察仔细的好孩子，如果用字母a表示图形内部的钉子数，则可以将图形规律表示为：当a=1时，则S=b÷2。

2. 变化方法，建构规律

师（拾级而上）：下面再请大家试着在钉子板上任意围出3个不同的多边形，使其内部有2颗钉子，并填写表1。

（教师提出问题后，学生自主地开展小组合作学习，在观察、比较、辨析、讨论、争辩之后有了发现）

师：经过一段时间的探究，想必你们都有了自己的发现，下面每个小组派一个代表进行分享。（不少组别的学生都有了发现，争先恐后地想要表达自己的观点）

生1：多边形的面积不等于边上钉子数的一半，比一半多1。

生2：与我们组的发现相同。（其他两个组也纷纷表示有了相同的发现）

师：没有发表观点的小组有没有其他想法呢？愿意同我们说一说吗？

生3：其实我们组也有相同的发现，只是没有汇报。

生4：我们组在操作的时候画错了一个图形，里面围了3颗钉子。

师：那另外两个符合要求的图形可以得出这个规律吗？

生4：可以。

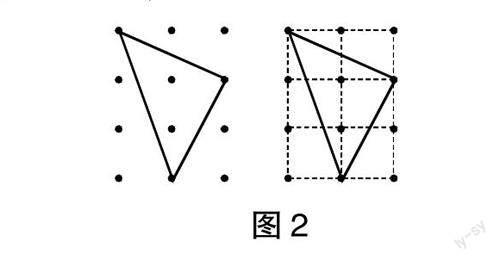
生5：我们小组在围图形的时候，将图形不满整格视为半格数计算，得出面积是3，然后感觉错了。

师：那我们就一起来看看他们小组围成的图形面积究竟应该是多少。（出示图2）

……

课堂教学推进到此时，笔者发现已经与教学设计出现了较大的偏差。之后笔者依旧“循规蹈矩”地组织了规律的完善与验证环节，并完成了教学任务。但是这一节课结束后，笔者深感疲惫，整节课没有达到预期的教学效果，同时课堂中专题活动的氛围并没有很好地体现出来，学生也没有发挥出自身的主体地位，使得教学效果不尽如人意。

（二）初次教学尝试的反思

笔者的初次教学尝试中反映出来的“误区”主要体现在以下方面：

首先，在初步探究中，引导学生观察图形并得出“内部有1颗钉子”的活动设计不当。不当之处主要体现在所有的思维活动没有在实践操作中开展，学生没有产生主动探究的意愿，一切观察和探究活动都是出于教师与教材的要求。

其次，在学生动手操作围图形中，由于操作过程的偏颇得出了特殊的图形，直接将学生的探究关注点引向了它处，形成了探究障碍；同时，倘若去掉探究过程，只安排之后的观察和分析活动，学生一样也可以探寻到其中的规律，因此这样的教学设计是否合理有待斟酌。

事实上，就整节课而言，并没有让学生感受和体验数学发现的过程，学生也没有在“从1到2，再从2到3，直至无限”的规律发现中不断进取，感受数学发现的喜悦。

（三）反思后的行为跟进——第二次尝试

基于以上诸多想法和思考，笔者在反思和提炼之后拾级而上，进行了第二次教学尝试。

1. 初次感知，有所认识

探究活动1.在钉子板上任意围出一个图形，并用自己的方法求一求图形面积。

（学生在自主探究之后进行汇报和展示，气氛热烈）

生1：我用数方格的方法计算得出这个图形的面积。

生2：我是用公式计算的。

师：那就让我们一起来看一看你们所围的图形，大家仔细观察，说一说这些图形有何特征，其面积大小与什么有关。（学生展开了热烈的讨论，很快有了发现）

师：根据你们的发现得出所有图形的顶点都在钉子上，一般来说我们将这样的图形称为“钉子板上的多边形”。（出示课题）这些多边形面积与内部的钉子数及边上的钉子数相关。

師：在研究中，我们一般通过先确定其中一个数量大小，然后研究其余两个数量的关系来研究三个数量间的关系。比如，这里大家围出的图形中内部钉子数都是1，那就让我们从这种内部有1颗钉子的图形开始今天的探究之旅。

2. 初步探究，发现规律

探究活动2.

第一步：独立在钉子板上任意围出一个多边形（要求：多边形的内部仅有1颗钉子）；

第二步：数出该多边形边上有多少颗钉子，并通过自己擅长的方法计算该多边形面积；

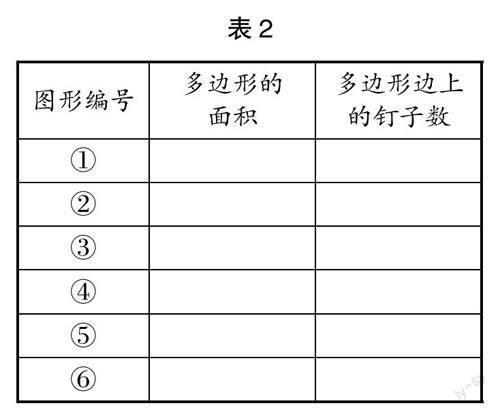
第三步：组内所有学生的结果汇总，填写统计表2；

第四步：小组合作学习并观察表内数据，你能发现什么？请在组内畅所欲言，大家相互分享自己的发现。

（学生在活动的引导下，循序渐进地进行数学探究，在观察、思考、探索、交流中有了很多发现）

最终汇总得出：内部钉子数是1时，多边形面积＝边上钉子数÷2。

师（提炼总结）：如果用字母S表示多边形的面积，a表示内部钉子数，b表示钉子数，则可以用“当a=1时，S=b÷2”来阐述此时它们的关系。

3. 深入探究，完善建构

师：那么，在刚才研究的基础上，如果边上的钉子数不改变，内部钉子数发生变化，结果会怎么样呢？下面请大家观察刚才自己围出的图形，并思考：基于原题，如何保证边上的钉子数不变，迅速将内部的钉子数变成2？（此问题具有很强的探究性，学生自主地开展独立操作，很快有了自己的想法，并在小组内进行了互动交流）

生：只需将多边形的一条边向外拉动。

师：非常好，让我们继续进一步的研究。

探究活动3.

第一步：学生独立改造和变化之前的图形，使得边上的钉子数不变，且得出一个内部有2颗钉子的新图形；

第二步：观察新图形，并思考新图形的面积是多少，相较于之前多了多少；

第三步：小组合作学习，相互分享各自的发现。

学生又一次积极地进行探究，在师生的共同提炼下得出：当内部的钉子数a=2时，可得S=b÷2+1。

4. 變化图形，建构规律

师：当内部的钉子数是3或4，或是更多时，面积S会如何变化呢？请大家进一步研究。

探究活动4.

第一步：变化图形内部的钉子数，由3到4，或者更多，保证边上的钉子数不变，将得出的面积与内部钉子数为1时相比较，得到什么发现；

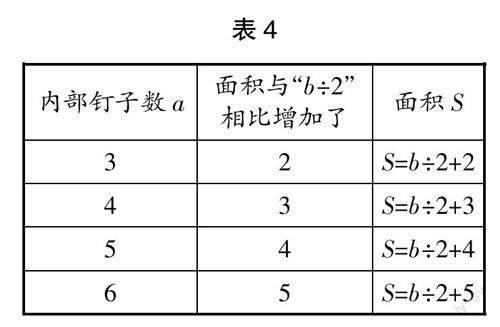
第二步：全组有序汇总组内所有成员的发现，填写表3；

第三步：一起观察表3中的数据，你能发现什么？

学生在共同努力下，生成了表4所示的研究成果，并在分析与交流之后得出：S=b÷2+a-1。

5. 操作验证，有所生成

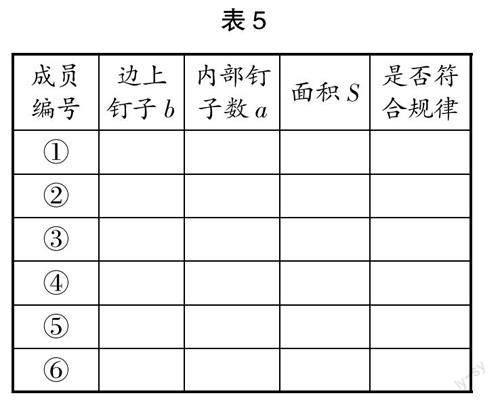
探究活动5. 上述规律，是否只要是钉子板上的多边形都适用呢？请学生独立思考和操作，在钉子板上围一围看有何发现，然后小组内成员汇总相关数据，并填写表5，以验证规律是否正确。

在深度探究和合作交流之后，学生交流了一种特殊情况，即（内部无钉子数的情形），并获得了新的认识。

6. 总结归纳，深化认识

师：本节课我们一起研究了“钉子板上的多边形面积”，回忆整个研究过程，我们先从内部1颗钉子开始，直到多颗钉子，运用从特殊到一般的方法去研究和发现规律，再以自己的方式去验证规律是否正确。事实上，这种方法也是数学家在发现规律时采用的方法，你们有了像科学家一般的研究经历。希望今天的探究经历让你们记忆犹新，并能够应用到之后的学习和研究中去。今天你们的发现也正是著名数学家皮克发现的皮克定理，《格点与面积》这本书着重介绍了与之相关的知识，对其感兴趣的学生可以利用课余时间去进一步了解。

三、教学反思和感悟

（一）以动手操作为载体，提升专题活动的有效性

手与脑存在着千丝万缕的联系，这些联系可以相互促进，让手变得更加富有创造性，让脑变得更加聪明。那么教师就需赋予学生更多的操作性活动，让学生在“做数学”的过程中获取知识、发展能力、生成智慧。比如，本节课在初次尝试中可以明显看出学生的动手操作活动无序、无力、无效。基于此，笔者在第二次尝试中设计的5次探究活动都离不开动手操作，让有序、高频的动手操作贯穿整节课，让学生“动”起来，在动手操作与数学思维的紧密联系中高效完成教学目标，提高了专题活动的有效性，促进了学生规律的发现和思维的发展。

（二）以探究性问题为驱动，彰显数学探究的思维性

数学规律是抽象静止的，而小学生都是生动活泼的生命个体。如果教师将抽象静止的数学规律直接“抛”给学生，让学生通过应用来深化认识，势必会导致学生思维的僵化。学生往往只能简单地套用规律，一旦涉及灵活运用则常常思维卡壳。规律的教学需要着重关注发现的过程，每一个探究活动都需以问题为驱动，让问题引领整个数学探究历程，这样才能充分展现数学探究的思维性。

比如，在本课的第二次教学尝试中，笔者设计的5次探究活动无一例外都是以问题延伸开来的，为学生搭建好平台，让学生积极主动去观察、分析、发现、思考、验证，让学生的思维更具开放性，让数学课堂时时迸发出思维的火花。

（三）以循序渐进的活动设计为指引，体现数学发现的递进性

想要体现数学发现的递进性，就需要为学生设计层层递进的数学探究活动，让学生触及数学本质，真正意义上感受和体验新规律的发现和构建过程。本课中，教师设计了循序渐进的5次探究活动，从特殊到一般地指引学生进行数学研究，使其感受数学探究的愉悦、数学发现的递进、数学知识的魅力，从而实现高效建构。

四、结语

总之，教与学相辅相成，数学课堂不仅需要教师尽心地教，也离不开学生积极主动地学，需要学生认真观察、细心思考、主动发现、自主探究和合作学习。提高课堂实效的方法与途径很多，需要教师以先进的教学理念来指导自身的教学实践，精心设计教学过程，通过课堂实践的磨砺来创造真实、开放、有效的数学课堂，才能让自身的教学风格得到塑造，让每个学生在课堂中有所得、有所获，让学生在数学发现中全面和谐发展，最终建构高效数学课堂。只有这样精心构造，才能让教师的专业素养快速发展起来，真正跟上新课程改革的脚步。