基于星地协同的降水数据插值方法及其适用性*
徐 勇,郭振东,盘钰春,郑志威
基于星地协同的降水数据插值方法及其适用性*
徐 勇,郭振东,盘钰春,郑志威
(桂林理工大学测绘地理信息学院,桂林 541006)
以长江中下游地区为研究区,协同地面气象站点降水数据和TRMM以及GPM卫星降水数据,利用六种Anusplin插值模型,基于验证站点实测降水数据对比分析星地协同降水数据插值结果与单一的TRMM和GPM降水数据、TRMM和GPM降尺度降水数据,以及基于地面气象站点插值降水数据的优劣,进而为获取地面气象站稀缺地域的高精度、高分辨率以及优良的空间细节性降水数据提供理论支撑。结果表明:(1)2001−2019年长江中下游地区TRMM(R2=0.81,BIAS=0.06,RMSE=171.1mm)和GPM星地协同插值方案(R2=0.81,BIAS=0.07,RMSE=172.8mm)各模型结果多年平均精度优于地面气象站点(R2=0.66,BIAS=0.02,RMSE=198.66mm)插值方案各模型、TRMM降尺度(R2=0.79,BIAS=0.06,RMSE=174.8mm)和GPM降尺度(R2=0.81,BIAS=0.09,RMSE=192.4mm)多年平均精度。(2)星地协同插值结果在降水数据空间细节表达、图像完整性以及模型稳定性上具有明显的优势,TRMM星地协同插值方案模型五插值效果最优。(3)Anusplin插值模型的变量、样条次数对地面气象站点插值结果精度影响显著,但对星地协同插值结果的影响微弱。(4)降尺度模型受辅助变量影响,会对降尺度结果造成一定的精度损失和图像残缺。
长江中下游地区;星地协同;TRMM;GPM;降尺度;Anusplin插值模型
降水是地球物质交换和生态循环的重要载体[1−3],与区域生态环境质量[4]、气象水文条件[5]、植被生长状况[6]等息息相关。因此,获取高精度、高分辨率的降水数据对农业生产和区域生态环境保护等具有重要意义。目前,降水数据主要通过降雨雷达、地面气象站点和卫星测雨三种方式获取[7]。其中,降雨雷达受环境影响较大,实际应用中适用性相对较低[8]。地面气象站数据精度较高,应用最为广泛,往往采用空间插值法来反映降水的时空分布特征,其中,平滑样条法(Anusplin插值法)相较于其它插值方法优势明显[9−11]。Anusplin插值法是一种平滑样条函数对多变量数据进行分析插值的工具,既考虑地形对降水量的影响,还考虑了气象站点分布及数量对降水插值的影响[9]。Tan等[10]研究结果表明,相较于反距离插值法(Inverse Distance Weight, IDW)、混合逻辑回归(Mixed Logistic Regression, MLR)和随机森林(Random Forests, RF)模型,Anusplin模型对中国降水和气温插值结果误差更小。Guo等[12]使用Anusplin对中国降水数据进行了插值,结果表明旱季降水插值结果的平均误差、平均绝对误差和均方根误差都小于湿季。徐翔等[13]通过Anusplin插值模型对康滇区多年月平均降水进行插值,且与IDW和普通克里金(Ordinary Kriging,OK)插值法进行对比,得出Anusplin更加适合山地地形的空间插值。谭剑波等[14]采用Anusplin插值法和克里金插值法对青藏高原东南缘年累计降水进行插值,得出Anusplin的插值效果优于克里金空间插值法。以上研究都证明了Anusplin插值法相较于其他插值方法具有一定的优越性,但插值精度受点位密度和空间分布等影响较大,具有一定的局限性。
卫星数据具有覆盖范围广、空间连续性强、所受地形制约小等特点,是降水信息获取的重要途径[15−18],其中,热带降水观测计划(Tropical Rainfall Measuring Mission,TRMM)卫星和全球降水观测计划(Global Precipitation Measurement,GPM)提供的遥感数据是目前最常用的两种遥感降水数据源[19−21]。但是TRMM和GPM降水数据空间分辨率较低,分别为0.25°×0.25°和0.1°×0.1°,因此,国内外学者对以上两种数据进行了降尺度研究,以提高其空间分辨率。Zhang等[22]在考虑植被NDVI和高程的基础上对三江源地区TRMM降水数据进行了降尺度研究,结果表明,降尺度后的结果空间分辨率上有显著提高,且降尺度结果与实测数据的相关性也得到了一定提升。Wang等[23]对祁连山地区GPM数据进行了降尺度,得出降尺度降水数据的精度高于原始数据,但高纬度地区降尺度结果精度明显低于区域平均值。崔路明等[20]对黄河流域、长江流域和珠江流域的TRMM和GPM降水数据进行降尺度,得出两种卫星数据的空间分辨率在降尺度后得到显著提升,但是其精度对原始数据依赖大,没有显著提升。以上研究结果表明,TRMM和GPM降尺度能够有效提升数据空间分辨率和空间细节性,但地形、纬度以及辅助变量的差异对于降尺度的结果也存在较大影响。
综上可知,无论是基于气象站点的空间插值还是卫星降水数据的降尺度,都具有得天独厚的优势以及各自的弊端。然而,已有研究大多局限于使用同一数据源生成更高空间分辨率的降水数据,少有研究将地面气象站点与卫星数据相结合,生成高精度、高分辨率的降水数据。因此,本文以长江中下游地区为研究区,基于Anusplin插值模型,融合地面气象站点与卫星降水数据,获得更高空间分辨率的降水数据,并分别与TRMM和GPM降水数据、TRMM和GPM降尺度数据以及单一的地面气象站点插值结果进行精度对比和适用性分析,以期为地面气象站稀缺地域的环境保护、经济建设以及预防洪涝灾害等提供数据支撑。
1 资料与方法
1.1 研究区概况
长江中下游地区包括湖北、安徽、江苏、湖南、江西、浙江和上海7个省(市),地理位置为24°39′N− 35°7′N,108°22′E−122°56′E,地形总体呈现“西南高、东北低”的空间分布格局,海拔最低处为–70m,最高处可达2944m(图1)。长江中下游地区是中国经济最发达的地区之一,该地区受季风气候影响,降水丰沛,气候温暖湿润,且地势平坦,区域内河道纵横交错,湖泊星罗棋布,地表水和地下水资源丰富。受西太平洋副热带高气压等因素影响,该地区旱涝灾害频发[24]。
1.2 数据类型及其来源
1.2.1 地面气象站观测降水数据
基于站点的降水数据源于国家气象科学数据中心(http://data.cma.cn/site/index.html)提供的2001−2019年逐日降水量数据,并基于逐日降水数据合成2001−2019年各年年均降水量数据。研究区内共有无缺测值站点148个,选取84个随机分布的站点作为插值站点,其余64个作为精度验证站点,其如图1所示。
1.2.2 卫星降水数据
采用由NASA(https://search. earthdata.nasa.gov/)发布的2001−2019年TRMM 3B43(0.25°×0.25°)和GPM IMERG月降水数据(0.1°×0.1°)。经过格式转换、重采样、栅格投影、裁剪等操作,获得2001−2019年逐月TRMM和GPM卫星降水数据。
1.2.3 其余数据
降尺度所需要的辅助变量数据包括2001−2019年逐月归一化植被指数(Nominalized difference vegetation index, NDVI)和数字高程模型(Digital elevation model, DEM)数据。辅助变量数据均来源于中国科学院资源与环境科学数据中心(http:// www.resdc.cn /)。其中,植被NDVI数据的空间分辨率为1km×1km,时间分辨率为1个月,来源于Terra卫星MODIS传感器的植被指数数据MOD13A3。DEM数据来源于美国奋进号航天飞机的雷达地形测绘数据,经过重采样后,空间分辨率为1km×1km。
1.3 模型和实验方案
1.3.1 降尺度模型及方法
地理加权回归模型(Geographically Weighted Regression,GWR)是Brunsdon等[25]提出的一种用于研究空间异质性的局部参数预测方法,GWR模型在遵循地理学第一定律的前提下,依据数据的地理位置信息计算衰减函数,从而得出局部回归方程的各项权重。通过估算每一地理位置的自变量和因变量参数建立回归模型[7],对数据进行降尺度计算。其基本公式为


以植被NDVI、高程和坡向作为GWR模型的辅助变量,以TRMM降水数据降尺度为例,同理可得GPM降尺度数据。具体步骤为,(1)将植被NDVI、高程、坡向、经度和纬度数据分别提取至与TRMM(0.25°×0.25°)相同的分辨率;(2)通过栅格转点和多值提取至点等操作将上述数据分别提取至TRMM的点矢量图上;(3)运用地理加权回归工具,将TRMM作为因变量,用植被NDVI、高程、坡向、经度和纬度作为自变量,选取自适应法(ADAPTIVE)作为核函数,内核带宽为交叉验证(CV),从而得到常数项、植被NDVI、高程、坡向、经度和纬度各自对应系数和残差项;(4)对常数项、对应系数和残差项运用反距离权重法(IDW)插值,并进行投影栅格操作,将其分辨率采样至1km×1km;(5)利用栅格计算器对分辨率为1km×1km的植被NDVI、高程、坡向、经度和纬度数据和重采样后的常数项、系数、残差进行回代,得到降尺度的TRMM数据。基于GWR模型的TRMM和GPM降尺度方案,如表1所示。

表1 地理加权回归模型(GWR)降尺度方案
1.3.2 Anusplin插值模型
利用Anusplin插值模型对单一的地面气象站点数据以及星地协同降水数据进行插值。Anusplin是基于普通薄盘函数以及局部薄盘样条函数插值理论,最早由澳大利亚学者Hutchinson等研发[26],其原理是采用平面平滑样条函数对多变量数据进行插值。局部薄盘光滑样条插值是对于其前身薄盘光滑样条的改进,除可以引入自变量外,还可以引入高程等线性协变量,即

式中,zi为空间第i点因变量,xi为d维样条独立变量,函数f(xi)是对xi进行估算的光滑函数,yi是p维的独立协变量,其系数为b,ei是均值等于零的自变量随机误差。
Anusplin插值模型允许引入多元线性因子模型,对时间序列的插值尤为适用。本文设计了基于地面站点的气象数据、TRMM星地协同数据和GPM星地协同数据下的三种插值方案,如表2所示。其中,Anusplin插值方案的设计是基于大量有关Anusplin插值研究中常见的变量组合(经度、纬度为自变量,高程为协变量/经度、纬度、高程为自变量)和样条次数(2、3、4)[27−28]以及三种不同的插值数据(单一的地面气象站点数据、地面气象站点数据协同TRMM卫星降水数据、地面气象站点数据协同GPM降水数据)的排列组合。其中,地面气象站点插值方案的插值数据是研究区内随机选取的84个插值地面气象站按照所设计的模型进行插值。TRMM和GPM星地协同插值方案的数据由上述84个用于插值的气象站点分别融合TRMM和GPM数据栅格,转点后随机选取900个TRMM数据点和900个GPM数据点,即如图2中的遥感卫星数据点,其中,TRMM数据点与GPM数据点位一致,最后分别形成984个TRMM和GPM星地协同数据点(图2)。
具体步骤如下:(1)将插值数据(xls文件)导入SPSS,导出dat批处理文件。(2)将dat文件放置于Anusplin插件文件夹中,依据模型修改sp.txt中的样条次数、自变量与协变量等参数设置。(3)运行run.cmd,进行Anusplin插值。(4)对生成的grd文件进行格式转换、异常值处理等相关操作,得到最终结果。
1.3.3 模型模拟结果检验指标
选用决定系数(R2)、偏差(BIAS)和均方根误差(Root mean square error, RMSE)检验降尺度和插值方案下结果的精度[29],即


(5)


表2 地面气象站点数据、TRMM星地协同和GPM星地协同数据的Anusplin插值模型设计
注:方案I即地面气象站点插值方案,以研究区内随机选取的84个地面气象站点2001−2019年各年平均降水量为插值数据;方案II和方案III分别为TRMM和GPM星地协同插值方案,以984个TRMM和GPM星地协同数据点(84个地面气象站点与900个遥感卫星数据点融合)的2001−2019年各年平均降水为插值数据的方案;模型一、模型二和模型三代表以经度、纬度为自变量,高程为协变量,样条次数分别为2、3、4的插值模型。模型四、模型五和模型六代表以经度、纬度和高程为自变量,样条次数分别为2、3、4的插值模型。TVTPS2、TVTPS3和TVTPS4均为三变量薄盘光滑样条函数。
Note: Scheme I is the interpolation scheme of in situ meteorological stations. The average annual precipitation of 84 randomly selected in situ meteorological stations in the study area from 2001 to 2019 is taken as the interpolation data; Scheme II and Scheme III are the TRMM and GPM satellite ground cooperative interpolation schemes, respectively. The scheme uses the average precipitation of 984 TRMM and GPM satellite ground cooperative data points (84 ground meteorological stations and 900 remote sensing satellite data points are fused) in 2001−2019 as the interpolation data; Model 1, Model 2, and Model 3 represent interpolation models with longitude and latitude as independent variables, elevation as covariates, and spline times of 2, 3, and 4, respectively. Model 4, Model 5, and Model 6 represent interpolation models with longitude(LO), latitude(LA), and elevation(EL) as independent variables and spline degree of 2, 3, and 4, respectively. TVTPS2,TVTPS3 and TVTPS4 are three variable thin disk smooth spline function.

图2 星地协同点位空间分布
2 结果与分析
2.1 星地协同插值方案的精度评价和对比
2.1.1 地面气象站点插值
以2001−2019年各年地面气象站降水数据为插值数据,利用表2中地面气象站点插值方案中六种Anusplin插值模型分别进行处理,并以站点实测值对其进行精度验证,将所得结果的决定系数(R2)、偏差(BIAS)和均方根误差(RMSE)分别取多年平均值,结果见图3。由图中可见,六种方案的R2、BIAS和RMSE平均值分别为0.66、0.02和198.66mm,与地面气象站点实测数据整体拟合程度较高,其中,模型四的插值结果拟合程度最高,且稳定性最强,R2达到了0.72,BIAS和RMSE分别为0mm和168.43mm,模型六的插值结果拟合程度最低,且稳定性最差,R2为0.53,BIAS和RMSE分别为0.02和278.89mm。从样条次数上对比,模型一(样条次数为2)的整体精度明显优于模型二(样条次数为3)和模型三(样条次数为4),模型四(样条次数为2)的整体精度优于模型五(样条次数为3)和模型六(样条次数为4)。从变量方式上对比,模型一、模型二、模型三(以经度、纬度为自变量,高程为协变量)和模型四、模型五、模型六(以经度、纬度和高程为自变量)的精度差距较小。综上可知,基于地面气象站点的六种模型插值结果精度差距较大,总体上模型四的插值结果精度最高,模型六的插值结果精度最低,变量方式对插值精度整体影响较小,样条次数对插值精度有着较为明显的影响,在地面气象站点插值方案中,样条次数为2的插值模型精度更高。模型四的平均降水量的空间分布见图4。

图3 方案I(站点插值方案)中六种模型对84个地面气象站点年降水量(2001−2019年平均值)的插值结果与实测数据对比
2.1.2 TRMM星地协同插值
以2001−2019年各年TRMM星地协同降水数据为插值数据,利用表2中TRMM星地协同插值方案下六种Anusplin插值模型分别进行处理,并以站点实测值对其进行精度验证,所得结果的R2、BIAS和RMSE分别取多年平均值。如图5所示,2001−2019年TRMM星地协同六种模型间插值结果差距较小,2001−2019年TRMM星地协同插值方案下R2、BIAS和RMSE六种方案平均值分别为0.81、0.06和171.1mm,与气象站点实测数据整体拟合程度较高且稳定性较好。其中,模型五的插值精度最高,R2达0.81,BIAS和RMSE分别为0.06mm和170.03mm,模型五的平均降水量的空间分布见图6。由于六种模型间精度差距较小,因此,样条次数和变量方式对TRMM星地协同插值方案结果的精度影响并不明显。由上可知,基于TRMM星地协同数据的六种模型插值结果的精度差距较小,其中,模型五插值精度最高且精度年际变化稳定,适用性优良,样条次数和变量方式对该方案影响微小。

图4 方案I中模型四对2001−2019年年降水量平均值的插值结果

图5 方案II(TRMM星地协同)六种插值模型对984个数据点降水量(2001−2019年平均值)插值结果与实测数据对比
注:984个数据点包括84个地面气象站点和900个TRMM卫星数据点。图7同。
Note: 984data points include 84 ground meteorological stations and 900 TRMM satellite data points. The same as Fig.7.
2.1.3 GPM星地协同插值
以2001−2019年各年GPM星地协同降水数据为插值数据,利用表2中GPM星地协同插值方案下六种Anusplin插值模型分别进行处理,并以站点实测值对其进行精度验证,所得结果的R2、BIAS和RMSE分别取多年平均值。如图7所示,2001−2019年GPM星地协同六种模型间插值结果差距较小,2001−2019年GPM星地协同插值方案下R2、BIAS和RMSE六种方案平均值分别为0.81、0.07和172.8mm,与气象站点实测数据整体拟合程度较高且稳定性较好。其中,模型六的插值精度最高,R2达到0.81,BIAS和RMSE分别为0.07和171.68mm,模型六的平均降水量的空间分布见图8。GPM星地协同模型五2001−2019年R²、BIAS和RMSE的变化均较小,说明年际精度变化平稳,模型稳定性较强。由于六种模型间精度差距较小,因此样条次数和变量方式对GPM星地协同插值方案结果的精度影响并不明显。由上可知,基于GPM星地协同数据的六种模型插值结果的精度差距较小,其中,模型五插值精度最高且精度年际变化稳定,适用性优良,样条次数和变量方式对该方案影响微小。

图6 方案II中模型五对2001−2019年年降水量平均值的插值结果

图7 方案III(GPM星地协同)六种插值模型对984个数据点降水量(2001−2019年平均值)插值结果与实测数据对比
2.1.4 星地协同与地面气象站点插值方案结果精度对比
TRMM与GPM星地协同插值结果精度差距较小,TRMM星地协同各模型中,模型五插值结果最好,GPM星地协同各模型中,模型六插值结果最好,但TRMM星地协同模型五插值结果整体精度略优于GPM星地协同模型六插值结果。相较于地面气象站点插值方案,星地协同方案与实测数据的R2得到了显著提升,并且TRMM与GPM星地协同方案下的六种模型间插值结果精度差距微小,模型间的精度稳定性有了明显的优化和提升。钱永兰等[30]研究表明,增加站点数量可以进一步提高Anusplin插值结果的精度。因此,融合气象站点和遥感数据后,星地协同方案的数据量得到了大幅增加,进而极大地提升了插值结果精度。星地协同方案下的BIAS相较于气象站点插值方案有轻微上升,这是由于BIAS是用来表示数据与真值的偏离程度,而星地协同方案融入了遥感数据,与完全采用实测数据进行插值的气象站点插值方案相比,偏差会相对较大,但是变化幅度十分微小,依然可以满足精度的需要。星地协同方案模型一、模型四、模型五下结果的RMSE与气象站点插值方案接近,而星地协同方案模型二、模型三、模型六下结果的RMSE明显优于气象站点插值方案。从整体上看,星地协同方案相较于气象站点插值方案对RMSE有着更强的适应性。

图8 方案III中模型六对2001−2019年年降水量平均值的插值结果
不论是星地协同插值方案还是地面气象站点插值方案,其插值结果的精度年际变化较小,这体现出Anusplin插值随时间变异的稳定性较强。同时,样条次数和变量方式对星地协同插值方案的影响十分微弱,体现出星地协同插值方案受Anusplin插值参数影响较小,使用容错率较高,适用性较强。
综上所述,星地协同方案插值结果的精度明显优于气象站点插值方案,并且星地协同在精度稳定性、模型使用容错率等方面均有着不错的体现,TRMM和GPM星地协同方案下的所有模型中,TRMM星地协同方案模型五的整体精度最高。
2.2 星地协同插值方案与降尺度方案精度对比
2.2.1 TRMM和GPM降水数据精度评价
为了检验TRMM和GPM数据在研究区内的适用性,以站点实测值对其进行精度验证,并计算2001−2019年R2、BIAS和RMSE多年平均值。由图9可知,TRMM和GPM降水数据的R2分别为0.80和0.82,与气象站点实测数据整体拟合程度较高,但存在一定的偏差,BIAS分别为0.07和0.09,RMSE范围为180.4~186.1mm,存在一定的高估现象。TRMM和GPM降水数据的R2、BIAS和RMSE的年际变化均较小。综上所述,TRMM数据与GPM数据整体精度差距较小,GPM数据的R2更高,与实测数据的相关性更强,但TRMM数据的BIAS和RMSE更低,在数据的稳定性上更胜一筹。TRMM和GPM整体精度年际变化均较小。
2.2.2 TRMM和GPM降尺度方案精度评价
为比较TRMM与GPM降尺度结果在研究区内的准确性,以站点实测值对其进行精度验证,并计算2001−2019年R2、BIAS和RMSE多年平均值。由图10可知,TRMM和GPM降尺度结果的R2分别为0.79和0.81,与气象站点实测数据整体拟合程度较高,但存在一定的偏差,BIAS分别为0.06和0.09。RMSE分别为174.8mm和192.4mm,存在一定的高估现象。TRMM和GPM降尺度结果的R2、BIAS和RMSE的年际变化均较小。综上所述,TRMM降尺度结果与GPM降尺度结果精度差距较小,GPM降尺度结果的R2更高,与实测数据的相关性更强,但TRMM降尺度结果的BIAS和RMSE更低,在数据的稳定性上更胜一筹。TRMM降尺度结果和GPM降尺度结果整体精度年际变化较小,TRMM和GPM及其降尺度结果平均降水量的空间分布见图11。
2.2.3 星地协同插值方案与降尺度方案精度对比
相较于TRMM遥感数据(0.25°×0.25°)和GPM遥感数据(0.1°×0.1°),星地协同插值和降尺度结果空间分辨率均为1km×1km,数据在空间细节性上有了极大的改进,但星地协同插值结果的精度整体上优于降尺度结果的精度。其中,TRMM星地协同插值结果的R2相较于TRMM降尺度结果提升了2%,相关性得到了一定的提升。GPM星地协同插值结果的BIAS和RMSE相较于GPM降尺度结果分别降低了2%和10%,稳定性得到了一定的提升。以上结果表明,在同等空间分辨率下,TRMM和GPM星地协同方案结果的精度优于降尺度方案的结果。相较于TRMM数据和GPM数据,星地协同方案结果的BIAS和RMSE均有了一定程度的改进,说明在融合地面气象站点后进行插值可以有效提升遥感数据的稳定性。

图9 2001−2019年TRMM和GPM数据平均值与实测数据散点图
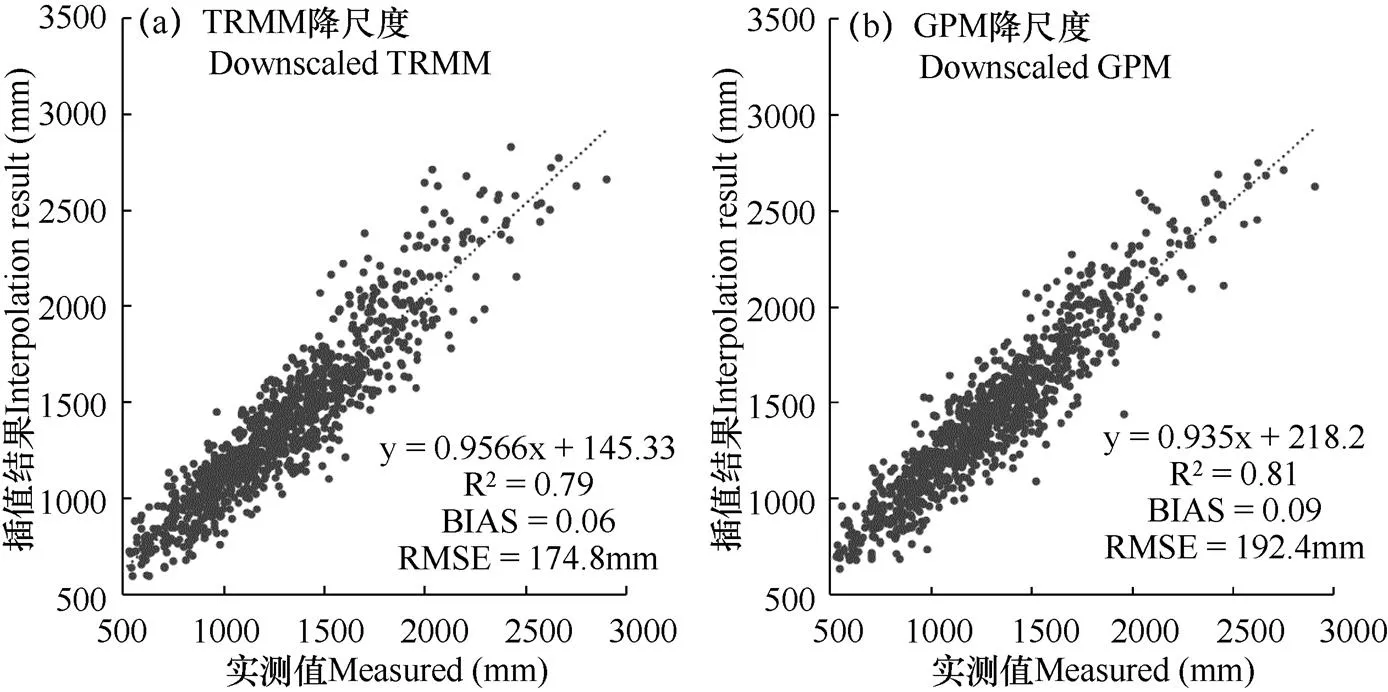
图10 2001−2019年TRMM和GPM降尺度平均值与实测数据散点图

图11 2001−2019年TRMM和GPM及其降尺度结果平均降水量的空间分布
3 结论与讨论
3.1 讨论
3.1.1 地面气象站点插值方案
气象站点插值方案的最优模型是以经度、纬度、高程为变量,样条次数为2的三变量薄盘光滑样条函数TVTPS2函数(模型四)。变量方式对地面气象站点插值方案的结果精度影响较小,但样条次数对结果精度的影响较为显著。这可能是由于长江地区地势相对平坦,区域内大部分为平原、丘陵地形[31],进而使得高程对Anusplin插值的影响显著性较低。气象站点插值方案对于偏差(BIAS)有着极强的适应性。但是对于不同的插值模型,其R2、BIAS和RMSE参差不齐且波动较大,这也体现出气象站点插值的精度十分依赖模型选择。其原因可能是因为参与插值的地面气象站点总量仅84个,较为稀疏,使得插值精度受到影响,这与孟清等[32]的结论基本一致。气象站点插值结果具有高分辨率(1km×1km)和优良的空间细节性。而降水空间分布往往具有一定的局域性,由陈金明等[33]的研究可知,长江流域降水具有一定的局域性和聚集度,但气象站点插值结果的降水空间分布细节上与高程空间分布细节具有较高的一致性。这可能是因为地面气象站点数据较少使得DEM数据在Anusplin插值中比重较大的缘故。这也说明在气象站点稀疏的情况下,Anusplin的插值结果会十分依赖DEM数据,导致其降水局域性特征不够明显。
3.1.2 TRMM和GPM降水数据及其降尺度方案
GPM数据在研究区内的R2优于TRMM数据,但BIAS和RMSE均大于TRMM数据。总体上,两种降水数据与真实值均存在较大的相关性,且GPM数据与实测数据的相关性优于TRMM数据,但是从数据的稳定性上来说,TRMM数据要优于GPM数据。金晓龙等[34]的研究中提到GPM使用了双频雷达观测系统(DPR)并利用站点数据进行矫正,这可能是GPM数据与实测数据相关性较强的原因,而GPM原始数据进行地面站点矫正后,其数据稳定性可能会受到一定的影响,从而使得其BIAS和RMSE相对较大。
GPM降尺度结果在研究区内的R2优于TRMM降尺度结果,但其BIAS和RMSE均大于TRMM降尺度方案结果,这与降尺度前的TRMM数据与GPM数据在R2、BIAS和RMSE的适应性上具有一致性。总体上,GPM降尺度结果与实测数据的相关性优于TRMM降尺度结果,但是从数据稳定性上来说,TRMM降尺度结果要更胜一筹。TRMM降尺度结果的R2相较于TRMM数据降低了1%,但是BIAS和RMSE均有了不同程度的改进。而对于GPM降尺度结果,R2相较于GPM数据同样降低了1%,但是BIAS和RMSE并未得到改进。TRMM降尺度结果与实测数据的相关性有所下降,但是稳定性有所提升,而GPM降尺度结果相关性和稳定性都有所下降。但无论是TRMM降尺度结果还是GPM降尺度结果,其R2、BIAS和RMSE均与未经过降尺度处理的TRMM和GPM数据相近,说明在研究区内降尺度所带来的精度损失是很小的。
在经过降尺度处理后,遥感影像分辨率由原来0.25°×0.25°和0.1°×0.1°提升至1km×1km,获得了更多的降水空间细节,说明对TRMM和GPM降水数据进行降尺度操作是可行的。值得一提的是,不论TRMM降尺度还是GPM降尺度,其结果均出现了残缺的情况,这可能是因为缺失部分为城镇、湖泊等无植被覆盖区域[31],植被NDVI值为0,导致了相应区域降尺度图像的缺失。同时,由白淑英等[35]的研究可知,植被NDVI存在一定的时滞效应,因此,在未考虑滞后期的前提下使用植被NDVI作为降尺度辅助变量,可能会对降尺度结果的精度产生一定影响。这也体现出降尺度模型在使用过程中需要考虑辅助变量的精度与适用性。
3.1.3 TRMM和GPM星地协同插值方案
TRMM星地协同最优插值模型是以经度、纬度、高程为变量,样条次数为3的三变量薄盘光滑样条函数TVTPS3函数(模型五),GPM星地协同最优插值模型是以经度、纬度和高程为变量,样条次数为4的三变量薄盘光滑样条函数TVTPS4函数(模型六)。TRMM星地协同最优插值结果的整体精度优于GPM星地协同最优插值结果。
同时,星地协同插值结果与实测数据的拟合程度、数据稳定性、时间变异性以及空间细节性上均有着不错的体现,继承了卫星数据的高拟合度和Anusplin插值的高稳定性、优良空间细节性的优点,符合预期期望。这可能是由于星地协同方案数据点量(984个)远大于地面气象站点数据量(84个),使得星地协同数据降水空间分布上兼顾了降水局域性和变化的渐进性,图像完整无残缺。在不同插值模型下,星地协同插值结果的精度较为稳定,方案使用的容错率较高,弥补了地面气象站点插值和降尺度模型各自的缺点。综上所述,星地协同插值结果具有高精度、高稳定性、高分辨率、高空间细节性以及使用高容错率等特点,不仅继承了卫星数据和Anusplin插值的天然优势,同时弥补了地面气象站点插值和降尺度模型的缺点,研究区内最适宜的星地协同插值模型为TRMM星地协同插值方案模型五。
3.2 结论
(1)星地协同插值结果的精度、图像完整性、空间细节表达以及模型使用的稳定性上均优于气象站点插值结果和降尺度结果,星地协同插值方案在长江中下游流域有着较强的适应性。
(2)地面气象站点插值方案结果的精度受插值模型的影响较大,尤其是受样条次数的影响较为显著,方案使用容错率较低,且图像呈现与DEM图像有较高的相似度,缺乏降水的局域性特征。
(3)研究区内TRMM和GPM降水数据与降尺度方案的结果均有较高的精度,但降尺度模型受辅助变量影响,会对遥感数据造成一定的精度损失和图像残缺。
(4)TRMM星地协同插值方案下的最优模型是以经度、纬度、高程为变量,样条次数为3的三变量薄盘光滑样条函数TVTPS3函数(模型五),GPM星地协同插值方案下的最优模型是以经度、纬度和高程为变量,样条次数为4的三变量薄盘光滑样条函数TVTPS4函数(模型六),TRMM星地协同最优模型插值结果的整体精度优于GPM星地协同最优模型,研究区内最适用模型为TRMM星地协同插值方案模型五。
[1] Zhang L,Schlaepfer D R,Chen Z,et al.Precipitation and evapotranspiration partitioning on the Three-River Source Region:a comparison between water balance and energy balance models[J].Journal of Hydrology:Regional Studies, 2021,38:100936.
[2] Qi W,Liu J,Xia J,et al.Divergent sensitivity of surface water and energy variables to precipitation product uncertainty in the Tibetan Plateau[J].Journal of Hydrology,2020,581:124338.
[3] Chu X,Han G,Wei S,et al.Seasonal not annual precipitation drives 8-year variability of interannual net CO2exchange in a salt marsh[J].Agricultural and Forest Meteorology, 2021,308:108557.
[4] Cheng Y,Zhan H,Yang W,et al.ISWCR 346:redistribution process of precipitation in ecological restoration activity of Pinus sylvestris var.mongolica in Mu Us Sandy Land, China[J].International Soil and Water Conservation Research,2022. doi:10.1016/j.iswcr.2022.03.008.
[5] 周芷菱,张利平,王惠筠,等.基于CMIP6的莱茵河流域极端水文事件变化特征研究[J].武汉大学学报(工学版), 2022,55(4):328-338.
Zhou Z L,Zhang L P,Wang H J,et al.Change characteristics of extreme hydrological events in the Rhine river basin based on CMIP6[J].Engineering Journal of Wuhan University, 2022,55(4):328-338.(in Chinese)
[6] Guerschman J P,Hill M J,Leys J,et al.Vegetation cover dependence on accumulated antecedent precipitation in Australia:Relationships with photosynthetic and non-photosynthetic vegetation fractions[J].Remote Sensing of Environment,2020,240:111670.
[7] 窦世卿,张寒博,徐勇,等.TRMM降水数据在长江流域的降尺度分析与校正[J].中国农业气象,2021,42(5):377-389.
Dou S Q,Zhang H B,Xu Y,et al.Research on downscaling and correction of TRMM data in the Yangtze river basin[J].Chinese Journal of Agrometeorology,2021,42(5): 377-389.(in Chinese)
[8] 冯克鹏,田军仓,洪阳,等.TRMM/GPM和Stage IV降水产品在小流域水文模拟效用评估[J].排灌机械工程学报,2021,39(4):397-403.
Feng K P,Tian J C,Hong Y,et al.Assessment of accuracy and runoff simulation of TRMM/GPM and stage Ⅳ precipitation products in small watershed[J].Journal of Drainage and Irrigation Machinery Engineering,2021, 39(4):397-403.(in Chinese)
[9] Zhao J,Li C,Yang T,et al.Estimation of high spatiotemporal resolution actual evapotranspiration by combining the SWH model with the METRIC model[J].Journal of Hydrology,2020,586:124883.
[10] Tan J,Xie X,Zuo J,et al.Coupling random forest and inverse distance weighting to generate climate surfaces of precipitation and temperature with multiple-covariates[J]. Journal of Hydrology,2021,598:126270.
[11] 张善红,白红英,齐贵增,等.基于多元线性回归模型和Anusplin的秦巴山区≥10℃积温空间模拟比较[J].水土保持研究,2022,29(1):184-189.
Zhang S H,Bai H Y,Qi G Z,et al.Spatial simulation of active accumulated temperature ≥10℃ in Qinling-Daba mountains based on Anusplin and Multiple linear regression model[J].Research of Soil and Water Conservation,2022, 29(1):184-189.(in Chinese)
[12] Guo B,Zhang J,Meng X,et al.Long-term spatio-temporal precipitation variations in China with precipitation surface interpolated by ANUSPLIN[J].Scientific Reports,2020, 10(1):1-17.
[13] 徐翔,许瑶,孙青青,等.复杂山地环境下气候要素的空间插值方法比较研究[J].华中师范大学学报(自然科学版),2018,52(1):122-129.
Xu X,Xu Y,Sun Q Q,et al.Comparision study on meteorological spatial interpolation approaches in Kangdian region of China[J].Journal of Central China Normal University, 2018,52(1):122-129. (in Chinese)
[14] 谭剑波,李爱农,雷光斌.青藏高原东南缘气象要素Anusplin和Cokriging空间插值对比分析[J].高原气象, 2016,35(4):875-886.
Tan J B,Li A N,Lei G B.Contrast on Anusplin and Cokriging meteorological spatial interpolation in southeastern margin of Qinghai-Xizang plateau[J].Plateau Meteorology,2016,35(4):875-886. (in Chinese)
[15] 玉院和,王金亮.TRMM 3B43降水数据在云南地区的降尺度适用性评价[J].中国农业气象,2020,41(9):575-586.
Yu Y H,Wang J L.Applicability evaluation of TRMM 3B43 precipitation data for downscaling in Yunnan province[J]. Chinese Journal of Agrometeorology,2020,41(9):575-586. (in Chinese)
[16] Zhang Y,Wu C,Yeh P J F,et al.Evaluation and comparison of precipitation estimates and hydrologic utility of CHIRPS,TRMM 3B42 V7 and PERSIANN-CDR products in various climate regimes[J].Atmospheric Research,2022, 265:105881.
[17] Shen Z,Yong B,Yi L,et al.From TRMM to GPM,how do improvements of post/near-real-time satellite precipitation estimates manifest[J].Atmospheric Research,2022:106029.
[18] Arshad M,Ma X,Yin J,et al.Evaluation of GPM-IMERG and TRMM-3B42 precipitation products over Pakistan[J]. Atmospheric Research,2021,249:105341.
[19] Lin Q,Peng T,Wu Z,et al.Performance evaluation,error decomposition and tree:based Machine Learning error correction of GPM IMERG and TRMM 3B42 products in the Three Gorges Reservoir area[J].Atmospheric Research, 2022,268:105988.
[20] 崔路明,王思梦,刘轶欣,等.TRMM和GPM卫星降水数据在中国三大流域的降尺度对比研究[J].长江流域资源与环境,2021,30(6):1317-1328.
Cui L M,Wang S M,Liu Y X,et al.Comparative study on downscaling of TRMM and GPM satellite precipitation data in three major river basins in China[J].Resources and Environment in the Yangtze Basin,2021,30(6):1317-1328. (in Chinese)
[21] 宁珊,张正勇,刘琳,等.TRMM偏最小二乘降尺度降水模型在新疆不同地貌的适应性[J].农业工程学报,2020, 36(12):99-109.
Ning S,Zhang Z Y,Liu L,et al.Adaptability of precipitation estimation method based on TRMM data combined with partial least squares downscaling in different landforms of Xinjiang,China[J].Transactions of the Chinese Society of Agricultural Engineering,2020,36(12):99-109.(in Chinese)
[22] Zhang T,Li B,Yuan Y,et al.Spatial downscaling of TRMM precipitation data considering the impacts of macro- geographical factors and local elevation in the Three-River Headwaters region[J].Remote Sensing of Environment, 2018,215:109-127.
[23] Wang H,Zang F,Zhao C,et al.A GWR downscaling method to reconstruct high-resolution precipitation dataset based on GSMaP-Gauge data:a case study in the Qilian Mountains, Northwest China[J].Science of the Total Environment, 2022,810:152066.
[24] 王小杰,夏军强,李启杰,等.长江中下游地区洪涝灾情时空变化及影响因素[J/OL].水资源保护, http://kns.cnki. net/kcms/detail/32.1356.TV.20220520.1357.012.html,2022-05-24.
Wang X J,Xia J Q,Li Q J,el al.Spatio-temporal distribution of flood disasters and influencing factors in the Middle and Lower Yangtze River Zone[J/OL].Water Resources Protection, http://kns.cnki.net/kcms/detail/32.1356.TV.20220520.1357.012.html,2022-05-24.(in Chinese)
[25] Brunsdon C,Fotheringham S,Charlton M.Geographically weighted local statistics applied to binary data[C]// International Conference on Geographic Information Science.Springer,Berlin,Heidelberg,2002:38-50.
[26] Hutchinson M F,Xu T.Anusplin version 4.2 user guide[J].Canberra:Centre for Resource and Environmental Studies,2004.
[27] 梅晓丹,李丹,王强,等.基于ANUSPLIN的小兴安岭地区降水格点数据空间插值[J].测绘与空间地理信息, 2021,44(12):7-10.
Mei X D,Li D,Wang Q,et al.Spatial interpolation of precipitation grid data in Xiaoxing′anling region based on ANUSPLIN[J].Geomatics & Spatial Information Technology, 2021,44(12):7-10.(in Chinese)
[28] 李任君,高懋芳,李强,等.基于ANUSPLIN的降水空间插值方法研究[J].中国农业信息,2019,31(1):48-57.
Li R J,Gao M F,Li Q,et al.Research on rainfall spatial interpolation method based on ANUSPLIN[J].China Agricultural Informatics,2019,31 (1):48-57.(in Chinese)
[29] 张寒博,窦世卿,温颖,等.遥感降水数据空间降尺度及干旱时空监测[J].水土保持学报,2022,36(1):153-160.
Zhang H B,Dou S Q,Wen Y,et al.Spatial downscaling of remote sensing precipitation data and spatiotemporal monitoring of drought[J].Journal of Soil and Water Conservation,2022,36(1):153-160.(in Chinese)
[30] 钱永兰,吕厚荃,张艳红.基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J].气象与环境学报,2010, 26(2):7-15.
Qian Y L,Lv H Q,Zhang Y H,et al.Application and assessment of spatial interpolation method on daily meteorological elements based on ANUSPLIN software[J]. Journal of Meteorology and Environment,2010,26(2): 7-15.(in Chinese)
[31] 刘文茹,居辉,陈国庆,等.典型浓度路径(RCP)情景下长江中下游地区气温变化预估[J].中国农业气象,2017,38(2): 65-75
Liu W R,Ju H,Chen G Q,et al.Prediction on the possible air temperature change over the middle and lower Yangtze River basin under the RCP scenarios[J].Chinese Journal of Agrometeorology,2017,38(2):65-75.(in Chinese)
[32] 孟清,白红英,郭少壮,等.基于Anusplin秦岭地区近50多年来的降水时空变化[J].水土保持研究,2020,27(2):207- 212.
Meng Q,Bai H Y,Guo S Z,el al.Spatial-temporal variation of precipitation in Qinling area in recent 50 years based on Anusplin[J].Reaserch of Soil and Water Conservation, 2020,27(2):207-212.(in Chinese)
[33] 陈金明,陆桂华,吴志勇,等.长江流域极端降水过程事件的年内分布特征[J].长江流域资源与环境,2014(4): 588-594.
Chen J M,Lu G H,Wu Z Y,et al.Inner-annual distribution characteristics of the extreme precipitation processes events over the Yangtze river basin.[J].Resources and Environment in the Yangtze Basin,2014(4):588-594.(in Chinese)
[34] 金晓龙,邵华,张弛,等.GPM卫星降水数据在天山山区的适用性分析[J].自然资源学报,2016,31(12):2075-2085.
Jin X L,Shao H,Zhang C,et al.The applicability evaluation of three satellite products in Tianshan Mountains[J].Journal of Natural Resources,2016,31(12):2075-2085.(in Chinese)
[35] 白淑英,王莉,史建桥.长江流域 NDVI 对气候变化响应的时滞效应[J].中国农业气象,2012,33(4) :579-586.
Bai S Y,Wang L,Shi J Q.Time lag effect of NDVI response to climatic change in Yangtze river basin[J].Chinese Journal of Agrometeorology,2012,33(4) :579-586.(in Chinese)
Interpolation Method of Satellite-ground Collaborative Precipitation and Its Applicability
XU Yong, GUO Zhen-dong, PAN Yu-chun, ZHENG Zhi-wei
(College of Geomatics and Geoinformation, Guilin University of Technology, Guilin 541006, China)
Changes in precipitation have great impacts on regional terrestrial ecosystems and water cycles. In this study, the middle and lower reaches of the Yangtze River Basin is considered to be the study area. The satellite-ground collaborative precipitation derived from in situ meteorological station, TRMM and GPM from 2001 to 2019 were collected. The interpolation results of satellite-ground collaborative precipitation against six Anusplin interpolation models were compared with the TRMM and GPM precipitation, TRMM and GPM downscaling precipitation, and interpolation precipitation based on the measured precipitation of verification stations. The research result can provide theoretical support for obtaining the precipitation with high accuracy, high resolution and excellent spatial details in the areas with sparse meteorological station. The results show that:(1)both the multi-year average accuracy of the results of the TRMM (R2=0.81, BIAS=0.06, RMSE=171.1mm)and GPM satellite-ground collaborative interpolation models(R2=0.81, BIAS=0.07, RMSE=172.8mm) in the middle and lower reaches of the Yangtze River Basin from 2001 to 2019 were superior to the multi-year average accuracy of interpolation precipitation of in situ meteorological stations(R2=0.66, BIAS=0.02, RMSE=198.66mm), TRMM downscaling precipitation(R2=0.79, BIAS=0.06, RMSE=174.8mm), and GPM downscaling precipitation(R2=0.81, BIAS=0.09, RMSE=192.4mm).(2)The satellite-ground collaborative interpolation precipitation has obvious advantages in the spatial detail expression, image integrity, and model stability. The interpolation result of TRMM satellite-ground collaborative interpolation model 5 has the best accuracy.(3)The variable and spline number of Anusplin interpolation model have a stronger impact on the accuracy of the interpolation result based on in situ meteorological station, but a weaker impact on the interpolation result based on satellite-ground collaborative interpolation precipitation.(4)The result of the downscaling model is closely related to auxiliary variables, which may cause a certain loss of accuracy and image deformity to downscaling precipitation data.
Satellite-ground collaborative; TRMM; GPM; Downscaling; Anusplin interpolation model
10.3969/j.issn.1000-6362.2023.08.007
徐勇,郭振东,盘钰春,等.基于星地协同的降水数据插值方法及其适用性[J].中国农业气象,2023,44(8):721-734
2022−09−26
广西自然科学基金项目(2020GXNSFBA297160);广西科技基地和人才专项(桂科AD21220133);国家自然科学基金项目(42061059;42161028);广西空间信息与测绘重点实验室项目(191851016);桂林理工大学大学生创新创业训练计划项目(202210596388)
徐勇,博士,副教授,主要研究方向为气候变化和植被覆盖反演,E-mail:yongxu@glut.edu.cn

