岩体渗透性变化对输水隧洞受力变形的影响

肖逸飞

(新疆额尔齐斯河投资开发(集团)有限公司,乌鲁木齐 830000)

1 概 述

在特殊地质条件及地形复杂地区修建输水隧洞,常常伴随高外水压力、高地应力等问题,严重影响输水隧洞的施工安全。针对深埋输水隧洞施工问题,许多学者通过理论法、试验法、监测法、数值法等不同手段开展了一系列研究。赵大洲等[1]以南水北调西线工程深埋长隧洞为研究对象,利用MIDAS有限元软件,建立含衬砌的输水隧洞模型,分析隧洞施工过程中衬砌管片的受力特征,评估了深埋隧洞施工过程的安全性。基于流-固耦合理论,纪佑军等[2]利用数值模拟手段模拟隧道开挖过程,对比考虑渗流和不考虑渗流下隧洞受力变形。贾善坡等[3]以深埋黏土岩隧道过程为例,基于渗流-应力耦合理论,分析了盾构隧道施工过程中衬砌管片受力变形的动态行为,进一步获得了围岩渗透压力分布特征。陈卫忠等[4]基于渗流耦合理论模型,通过ABAQUS二次开发,将渗流耦合模型考虑其中,计算分析了压力隧洞施工过程中围岩变形规律。王克忠等[5]以沭水东调引水隧洞为研究对象,通过数值模拟软件,对比渗流作用对隧道施工过程的影响,分析了围岩渗流场演变规律。周亚峰等[6]模拟计算了深埋TBM隧洞施工过程,研究了隧洞渗流动态演化规律。

本文以新疆某输水隧洞为研究对象,利用有限元软件,建立考虑渗透系数变化和不考虑渗透系数变化两种工况,分析隧洞排水和充水后不同工况下输水隧洞位移、孔隙水压力、塑性区的变化规律。

2 工程概况

新疆某输水隧洞包括支洞和主洞,支洞进口地面高程约799.451m,与主洞交点高程605.882m,长度1 543.215m;纵断面设计为:200m长12.9%的陡坡+20m长3%的缓坡,综合纵坡11.70%;支洞断面型式为城门洞型,断面尺寸6.7m×6.8m。主洞全长8.347km,隧洞纵坡1/2 583,起点底板顶高程607.565m,末点底板顶高程604.333m。地形地貌属于ALT山南坡WLGH河谷区和WLGH南岸剥蚀丘陵区,地势总体南高北低,海拔高程790～816m,河谷区地形平缓开阔,为河漫滩及河流阶地;南岸剥蚀丘陵区地形起伏较小,山顶多呈浑圆状,山体坡度较缓,一般高差10～30m,基岩大多裸露,主要为荒漠地貌。

3 有限元模型

根据输水隧洞的设计方案,建立宽度460m、高度640m的有限元模型,隧洞建在模型中间位置,见图1。

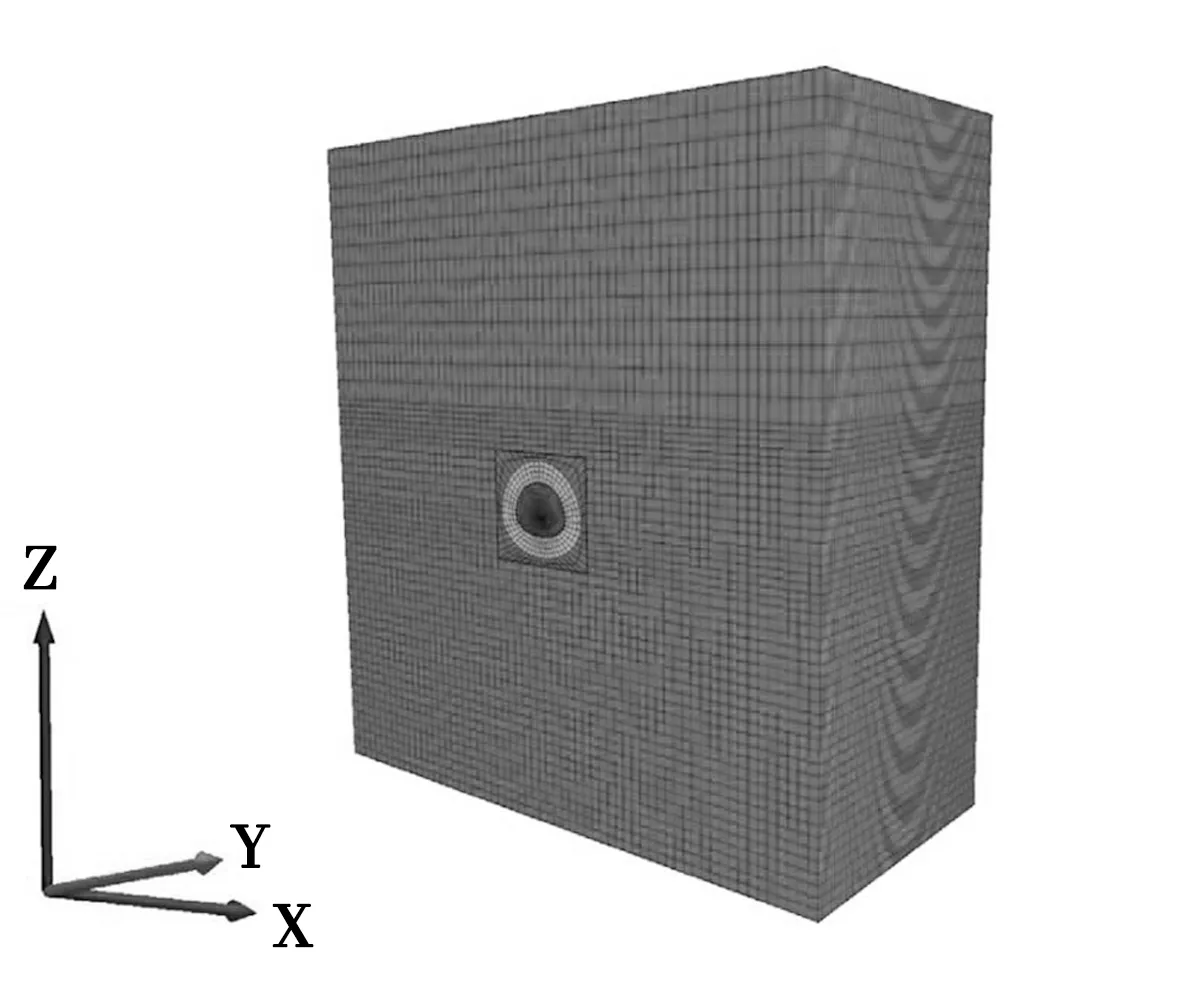
图1 有限元模型

所建模型位于地下水下方,因此模型中围岩为饱和状态。模型中,用四边形实体单元划分隧洞衬砌结构和围岩,模型顶部设置44.8MPa的自重应力,模型两侧和底部设为固定边界。此外,模型顶部和底部分别施加300和760m水头,水压在模型两侧呈梯形。参考现场地应力监测结果,输水隧洞的初始应力主要为自重应力,侧压力系数为0.88。根据地勘报告,衬砌和围岩物理力学参数见表1。

表1 衬砌和围岩物理力学参数

为研究围岩渗透系数演化对输水隧洞整体影响规律,建立考虑渗透系数变化和不考虑渗透系数变化两种工况:工况一设定渗透系数为恒定值;工况二设定渗透系数为基于体积应变的变化。

4 数值结果与监测结果对比

4.1 渗透系数变化规律

输水隧洞掘进后,对于工况二(考虑围岩渗透系数变化),渗透系数沿隧洞拱底和拱顶到围岩内部深处的变化曲线见图2。从图2可以看出,围岩渗透系数在输水隧洞掘进边界变化显著,在隧洞边界处拱底和拱顶渗透系数分别为1.0×10-3和3.3×10-3cm/s,沿着围岩深处先迅速降低随后缓慢降低直至趋于稳定。渗透系数相对于围岩初始渗透系数增大3个数量级,这个规律与实际工况相吻合,即围岩因地应力释放产生松动并衍生较多裂缝,从而导致围岩渗透性增大。

图2 渗透系数变化曲线

4.2 围岩位移变化

为保证深埋输水隧洞掘进过程的安全性,当隧道掘进后,通过钻孔在TI隧洞掌子面后方的拱顶和右拱腰位置布设深15m的位移计,监测隧道继续掘进掌子面后方变形。隧洞拱顶和右拱腰围岩变形监测值与数值模拟两种工况对比图见图3。

图3 围岩变形监测值与数值模拟两种工况对比图

从图3可以看出,在15m深度处,围岩位移监测值略小于数值模拟两种工况结果,其余位置的围岩位移监测值大于工况一结果,但小于工况二结果。在输水隧洞边界处(即距离为0m),围岩拱顶位移监测值比工况二结果小2.6cm,比工况一结果大2.7cm;围岩右拱腰位移监测值比工况二结果小4.1cm,比工况一结果大2.4m。由此可见,不考虑渗透系数变化的工况一数值结果偏小,且位移计只能监测隧洞开挖后的部分位移。因此,考虑到可靠性和安全性,考虑渗透系数变化的工况二更符合实际工况,结果更为合理、准确。

5 渗透性演化对隧洞稳定性影响分析

基于上一节验证的考虑渗透系数变化模型的合理性,本节分析运营期输水隧洞在排水和充水后,围岩渗透系数变化对围岩变形、孔隙水压力以及塑性应变的影响。仍然考虑渗透系数变化和不考虑渗透系数变化两种工况,模拟过程共5个步骤:

步骤1:设定初始地应力平衡,模型顶部和底部分别施加300和760m水头。

步骤2:隧道开始掘进,施工时长100h,隧道水压力迅速减小至0。

步骤3:激活隧洞衬砌,施工时长48h。

步骤4:设置输水隧洞内水压力水头100m,充水时长120h。

步骤5:设置输水隧洞进行4h的排水。

运营期输水隧洞在排水和充水后,其外水压力会发生变化,尤其当隧洞排水后,围岩外水压力会逐渐减小。图4(a)为充水后隧道拱顶孔隙水压力沿围岩深处方向的变化曲线。由图4(a)可知,两种工况拱顶孔隙水压力的变化规律略有差异。其中,工况一的围岩孔隙水压力沿围岩深处方向逐渐增大;而工况二的围岩孔隙水压力沿围岩深处方向先缓慢减小直至距隧洞3m处,随后缓慢增大。图4(b)为排水后隧道拱顶孔隙水压力沿围岩深处方向的变化曲线。由图4(b)可知,两种工况拱顶孔隙水压力的变化规律与隧洞充水情况相似。其中,工况一的围岩孔隙水压力持续增大;工况二的围岩孔隙水压力在隧洞3m范围内变化较小,随后持续增大。对比两图可以看出,工况一的孔隙水压力略大于工况二的孔隙水压力。

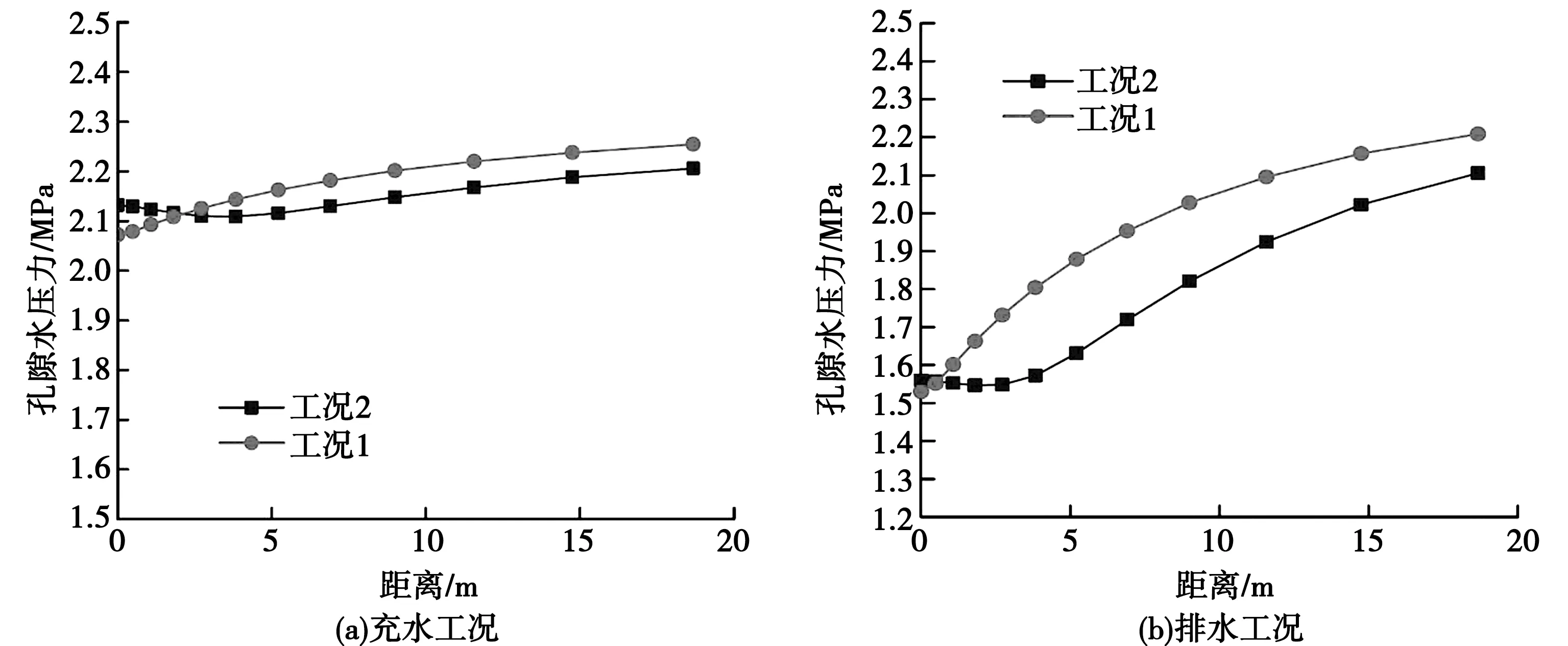
图4 孔隙水压力沿围岩深处方向的变化曲线

运营期输水隧洞在排水和充水后,其围岩位移也会发生变化。图5为隧道拱底和拱顶处围岩位移不同计算步骤下变化曲线。从图5可以看出,隧洞充水后,其拱顶位移略有减小;隧洞排水后,由于压力释放,拱顶位移略有增大;隧洞充水和排水后,拱底位移均略有增大,位移变化规律大致相同。对比两种工况的隧洞位移可知,工况二下隧洞拱底和拱顶位移均远大于工况一下围岩位移,即工况二下拱顶位移接近工况一下拱顶位移的两倍,工况二下拱底位移接近工况一下拱底位移的3倍。这是因为考虑隧洞周边围岩渗透系数迅速增大,从而引起隧洞附近围岩增大。数值计算结果与监测结果对比可知,隧道拱底和拱顶位移监测值介于数值计算两种工况之间,并且隧道拱底和拱顶位移监测结果的变化规律与数值计算两种工况基本相同,表明所建输水隧洞模型的正确性。

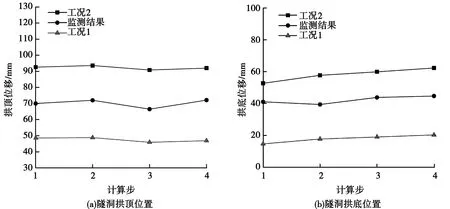
图5 围岩位移不同计算步骤下变化曲线

运营期输水隧洞在排水和充水后,其围岩塑性变形也会发生变化。隧道排水后右拱腰塑性应变变化曲线见图6。从图6可以看出,在隧洞洞壁位置,工况一和工况二塑性应变均到达峰值,分别为7.1×10-3和2.4×10-2。可见,因为考虑围岩渗透系数的变化,工况二下隧洞周边围岩塑性屈服程度更大。进一步观察图6可知,在输水隧洞右拱腰位置,工况一和工况二的塑性区范围分别为4.0和7.5m。而根据位移计监测结果可知,右拱腰松弛深度范围为6.0～7.0m。因此,从塑性区角度出发,考虑围岩渗透系数的变化更接近实际工况。

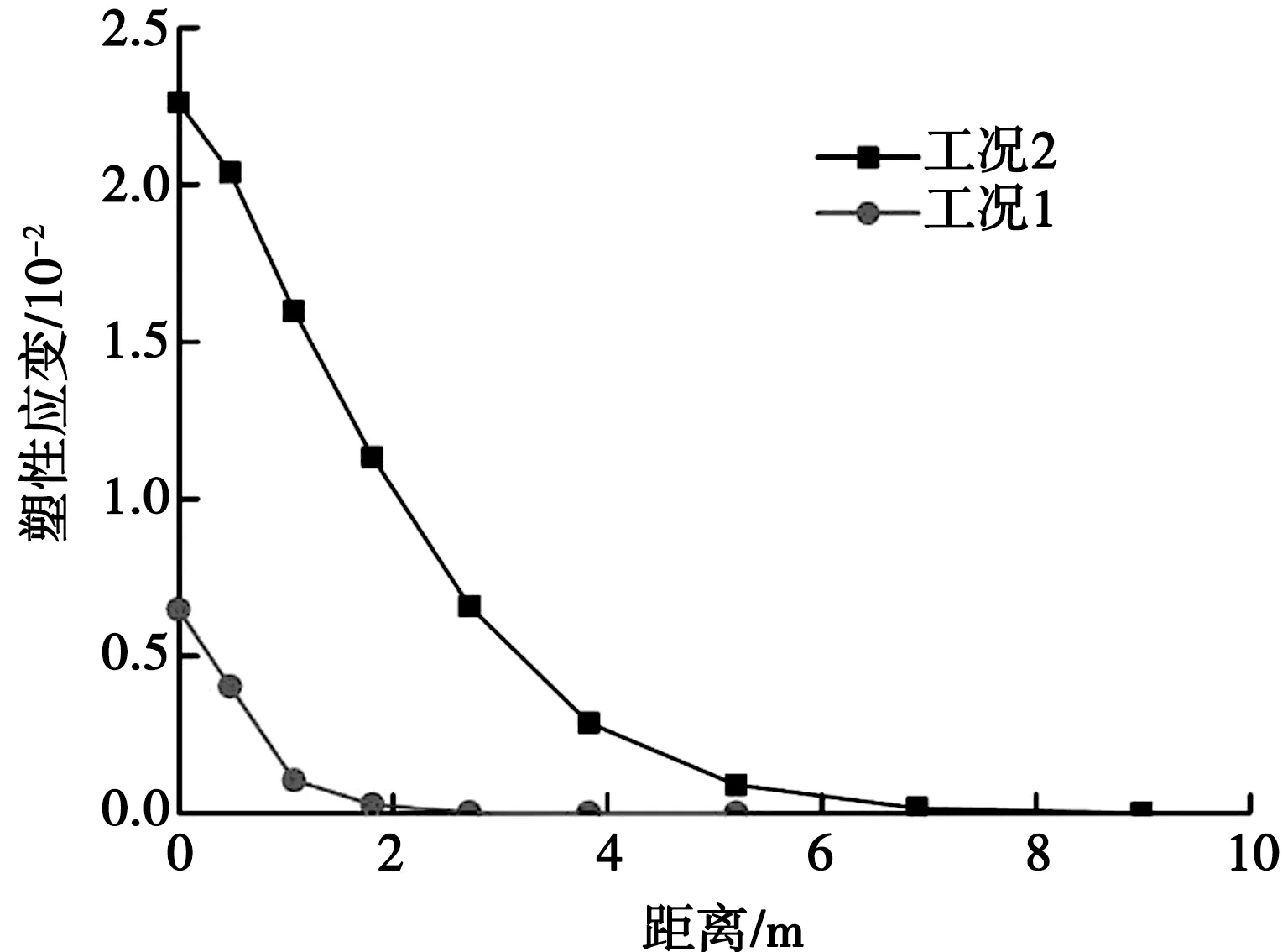
图6 隧道排水后右拱腰塑性应变变化曲线

图7为隧洞拱底和拱顶处塑性应变在不同计算步骤下变化曲线。

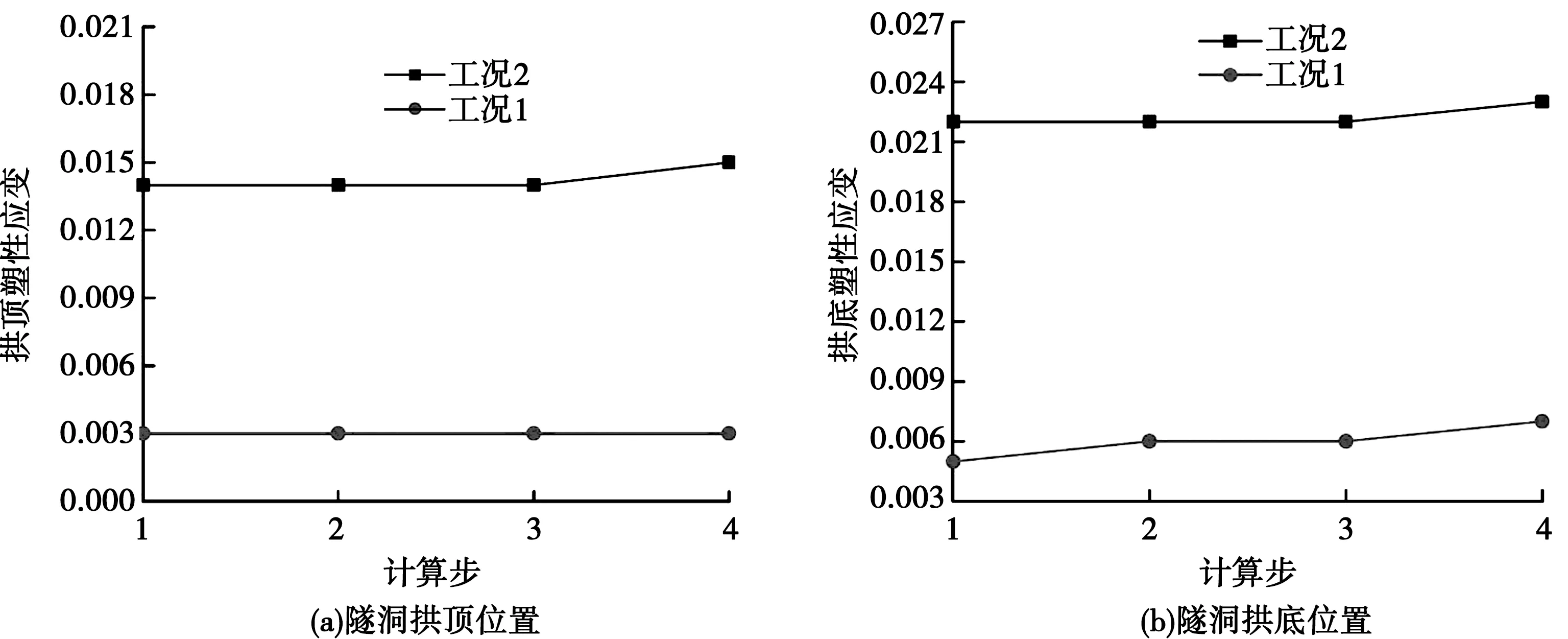
图7 隧洞拱底和拱顶处塑性应变在不同计算步骤下变化曲线

从图7可以看出,隧洞在充水和排水后,围岩塑性应变均随计算步而缓慢增大。在隧洞拱顶位置,工况一塑性区在隧洞充水和排水后变化较小,工况二塑性区在隧洞排水后增大。在隧洞拱底位置,隧洞充水和排水后,两种工况下隧洞塑性区范围均有所增大。

6 结 论

以新疆某输水隧洞为研究对象,利用有限元软件,建立了考虑渗透系数变化和不考虑渗透系数变化两种工况,分析了隧洞排水和充水后不同工况下输水隧洞位移、孔隙水压力、塑性区的变化规律。结论如下:

1)围岩渗透系数在输水隧洞掘进边界变化显著,在隧洞边界处拱底和拱顶均达到峰值,沿着围岩深处先迅速降低随后缓慢降低直至趋于稳定。

2)工况一的围岩孔隙水压力沿围岩深处方向逐渐增大,而工况二的围岩孔隙水压力沿围岩深处方向先缓慢减小直至距隧洞3m处,随后缓慢增大;考虑隧洞周边围岩渗透系数迅速增大,工况二下拱顶位移接近工况一下拱顶位移的两倍,而工况二下拱底位移接近工况一下拱底位移的3倍。

3)隧洞在充水和排水后,围岩塑性应变均随计算步而缓慢增大。在隧洞拱顶位置,工况一塑性区在隧洞充水和排水后变化较小,工况二塑性区在隧洞排水后增大。在隧洞拱底位置,隧洞充水和排水后,两种工况下隧洞塑性区范围均有所增大。

4)通过数值结果与监测结果对比,考虑渗透系数变化的工况二更符合实际工况,结果更为合理、准确。