分层拉丁超立方体抽样方法及应用
张艳,杨金语
(1.天津财经大学珠江学院数据工程学院,天津 301811;2.南开大学统计与数据科学学院,天津 300071)
0 引言
在经济、工程等领域的实际应用中,常需要估计某个指标的均值;在统计、数学等领域中,常需要估计某个复杂的定积分。然而,这些问题常常难以直接计算,此时可以借助蒙特卡罗方法模拟实现[1—3],其主要思想是通过计算机软件来模拟实践中的随机抽样[2]。常用的蒙特卡罗方法有随机投点法与平均值法,在相同的抽样方法以及样本容量(或试验次数)下,平均值法得到的估计量的方差小于等于随机投点法得到的估计量的方差[1],即平均值法得到的估计量精度更高。以一维情形为例,简述平均值法的主要过程如下:
设X~U(0,1),且:
由式(1)知,可以用数学期望的估计值作为式(1)的积分的估计值。从(0,1)上的均匀分布中抽取独立样本x1,x2,…,xn,利用样本均值估计μ的值,μ的估计值为:
其中,μ̂是μ的无偏估计量,̂的方差为:
当重复获取m个样本进行如上估计时,可得到估计量,则式(3)的方差可用式(4)进行估计:
为了获得μ的精度较高的估计量,方差缩减技术得到了广泛研究。常见的方差缩减技术主要包括对偶变量法、条件期望法、分层抽样法、控制变量法、重要性抽样法等[2]。这些方法的技巧主要分为以下四类:(1)只改变概率分布,比如重要性抽样法是把概率分布改为重要概率分布,而分层抽样是把整层概率分布改为分层概率分布;(2)只改变统计量,比如控制变量法与对偶变量法;(3)同时改变概率分布和统计量,比如条件期望法;(4)只改变统计特性,比如系统抽样和拟蒙特卡罗方法是把随机数改变为非随机数。这些方法均得到了广泛的研究与应用[3—6]。事实上,单个技巧降低方差的效果往往有限,因此可以使用组合技巧[3]。
综上所述,目前关于提高蒙特卡罗模拟估计精度的研究主要集中在方差缩减技术方面,而其中基于抽样方法角度研究蒙特卡罗模拟估计精度的文献较少。从式(2)至式(4)不难发现,样本点x1,x2,…,xn的质量直接决定着估计量方差的大小,即决定着估计量的精度,而这n个样本点质量的优劣又受到抽样方法的影响。此外,现有研究大多采用经典的抽样方法,比如简单随机抽样(Simple random sampling,SRS)、分层随机抽样(Stratified random sampling,STRS)、重要性抽样等[1—7],且将不同抽样方法进一步结合起来的更少。本文将基于抽样方法视角,借助试验设计思想,将分层抽样方法与拉丁超立方体抽样方法[8]相结合,提出一种新的抽样方法,以实现方差缩减,从而提高蒙特卡罗模拟的估计精度。
1 分层拉丁超立方体抽样
1.1 拉丁超立方体抽样的定义
在试验设计中,一个设计可用一个矩阵表示,称为设计阵。设计阵每一行对应一次试验,每一列对应一个试验因子,故设计阵的行数即为试验次数,列数即为试验包含因子的个数。拉丁超立方体抽样(Latin Hypercube Sampling,LHS)是McKay等(1979)[8]提出的一种估计响应函数总体均值的抽样方法,在计算机试验中应用广泛。与LHS对应的概念是拉丁超立方体设计(Latin Hypercube Design,LHD),LHS可由LHD变换而来。为此先介绍LHD的定义。
定义1:对于一个有n次试验、q个因子的设计阵,若其每一列均是1,2,…,n的随机排列,且各列是独立生成的,则称此设计为拉丁超立方体设计,记为LHD(n,q)。
由定义1可知,LHD中每个因子的水平数(因子取值的个数)均与试验次数相同,这使得LHD能更好地适应计算机试验不存在试验误差的特点,较大的水平数使其更具探索因子与响应之间复杂曲面关系的潜力。定义2说明了如何由一个LHD得到LHS。
定义2:给定一个LHD(n,q),不妨记为A=(aij)n×q,令:
其中,uij是[0,1)上的均匀分布随机数,则称B=(bij)n×q为有q个因子、样本容量为n的拉丁超立方体抽样,记为LHS(n,q)。
由定义2知,第j个因子的第i个水平经过式(5)的变换,由{1,2,…,n}标准化到区间(0,1]内,从而由一个LHD(n,q)得到空间(0,1]q中的拉丁超立方体抽样,即LHS(n,q)。相当于将空间(0,1]q等分成nq个小的超立方体,然后根据A=(aij)n×q的n行选出n个小的超立方体,再由第i行的q个均匀随机数ui1,ui2,…,uiq决定样本点在n个小的超立方体中的具体位置。这n个样本点满足如下性质:若把每一维区间(0,1]等分成n个小区间(0,1/n],(1/n,2/n],…,((n-1)/n,1],则将n个样本点向任一维度上投影时,每个小区间中包含且仅包含一个样本点。第j个因子的第i个水平决定了在第j个维度上投影点落在哪个区间中,而随机数uij决定了投影点的具体位置。下面给出一个例子,演示如何由一个LHD变换为相应的LHS。
例1:随机生成一个包含2个因子、8次试验的拉丁超立方体设计LHD(8,2),并通过式(5)将其变成一个LHS(8,2)。
将此LHS(8,2)的样本点标记在图1中,其中(0,1]2被等分成8×8=64个小正方形。从图1可知,LHS(8,2)的8个样本点所在的小正方形由LHD(8,2)的行决定,而在小正方形中的具体位置则受随机数uij(i=1,2,…,8;j=1,2)的影响。当把8个样本点向两个维度上投影时,每个维度上的8个等分区间(0,1/8],(1/8,2/8],…,(7/8,1]中均包含且只包含一个点。为了对比,随机生成一个包含8个样本点、2个变量的简单随机抽样,记为SRS(8,2),其散点图如图2所示。易见,在两个维度上的8个等分区间(0,1/8],(1/8,2/8],…,(7/8,1]中,有的区间中没有点,而有的区间中却有多个点。显然,在一维投影均匀性方面,LHS(n,q)要优于SRS(n,q)。

图1 LHS(8,2)的散点图
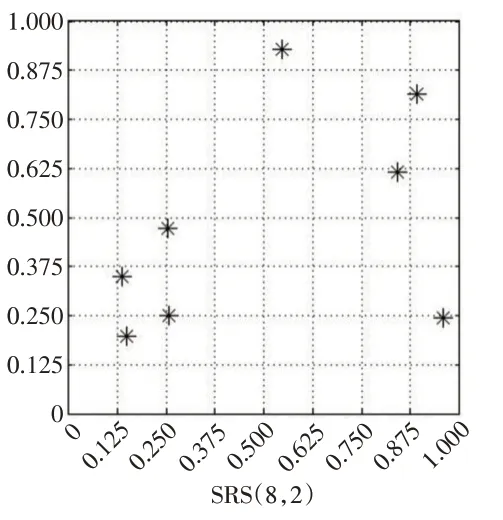
图2 SRS(8,2)的散点图
1.2 分层拉丁超立方体抽样的定义
不妨记有n个样本点、s个层,每层样本点数分别为t1,t2,…,ts的STRS为STRS(n,s;t1,t2,…,ts),其中n=t1+t2+…+ts。下面结合STRS与LHS的定义,给出分层拉丁超立方体抽样的定义。
定义3:在分层抽样的基础上,如果各层抽样是按拉丁超立方体抽样独立地进行的,那么这种抽样称为分层拉丁超立方体抽样(Stratified Latin Hypercube Sampling,STLHS)。记有n个样本点、s个层,每层样本点数分别为t1,t2,…,ts的STLHS为STLHS(n,s;t1,t2,…,ts),其中n=t1+t2+…+ts。
由定义3可知,STLHS与STRS的区别在于每层中的抽样方式不同。对于STRS,每层中的抽样是按简单随机抽样进行的;而对于STLHS,每层中的抽样是按LHS进行的。下面给出STLHS(n,s;t1,t2,…,ts)的抽样算法。
1.3 分层拉丁超立方体抽样的算法
本文将给出一维STLHS(n,s;t1,t2,…,ts)的两种算法。
(1)算法1
步骤1:给定分层个数s,将区间(0,1]等分为s个小区间(0,1/s],(1/s,2/s],…,((s-1)/s,1]。
步骤2:将第i层((i-1)/s,i/s]等分为ti个小区间,i=1,2,…,s,即:
步骤3:在式(6)中的每个小区间中,随机抽取一个样本点,得到第i层的ti个样本点,并将ti个样本点的顺序随机化。
步骤4:将各层样本点组合得到最终的总样本。
由算法1的步骤2以及定义2可知,第i层产生的样本点组成一个LHS(ti,1),i=1,2,…,s。再由定义3可知,所得抽样结果为一个分层拉丁超立方体抽样,具体为STLHS(n,s;t1,t2,…,ts)。
(2)算法2
步骤1:给定分层个数s,将区间(0,1]等分为s个小区间(0,1/s],(1/s,2/s],…,((s-1)/s,1]。
步骤2:对于第i层,随机生成一个LHS(ti,1),i=1,2,…,s。
步骤3:将第i层的LHS(ti,1)按式(7)进行变换:
步骤4:将各层样本点组合得到最终的总样本。
基于LHS,算法2更易实现,但算法2和算法1所得的抽样结果等价。
下面用例2对以上算法的结果进行展示。
例2:考虑随机生成一个STLHS(10,2;4,6),记为A,易见s=2,t1=4,t2=6。
先利用算法1生成。根据步骤1,将区间(0,1]等分为2个区间(0,1/2],(1/2,1];由步骤2,将(0,1/2]等分为4个区间(0,0.125],(0.125,0.250],(0.250,0.375],(0.375,0.500],将(1/2,1]等分为6个区间(0.500,0.583],(0.583,0.667],(0.667,0.750],(0.750,0.833],(0.833,0.917],(0.917,1];根据步骤3,在以上10个小区间中分别抽取一个样本点;最后,由步骤4将所有样本点合在一起即可得到STLHS(10,2;4,6)。
再根据算法2生成。根据步骤1,将区间(0,1]等分为2个区间(0,1/2],(1/2,1];根据步骤2,在两层区间(0,1/2]和(1/2,1]中分别生成LHS(4,1)和LHS(6,1);根据步骤3,将LHS(4,1)变换为[LHS(4,1)+1-1)]/2,将LHS(6,1)变换为[LHS(6,1)+2-1)]/2;最后,由步骤4将所有样本点合在一起即可得到STLHS(10,2;4,6)。
为了展示STLHS的均匀性,现随机生成一个STRS(10,2;4,6),记为B。两种方法下的抽样结果A与B如下所示:
为了更清晰地了解两种抽样的区别,现绘制A与B的散点图,分别如图3与图4所示。

图3 STLHS(10,2;4,6)样本点的分布图

图4 STRS(10,2;4,6)样本点的分布图
从图3可以看出,对于本文新提出的分层拉丁超立方体抽样STLHS(10,2;4,6)来说,第一层(0,0.5]的4个样本点分别分布在4个等距区间(0,0.125],(0.125,0.25],(0.25,0.375],(0.375,0.5]中,而第二层(0.5,1]的6个样本点分别分布在(0.5,0.583],(0.583,0.667],(0.667,0.75],(0.75,0.833],(0.833,0.917],(0.917,1]中,即在每一层中都实现最大程度的分层均匀性。从图4可以看出,对于分层随机抽样STRS(10,2;4,6)来说,在某些小区间中没有样本点(比如(0,0.125]),而在某些小区间中有多个样本点(比如(0.375,0.500]中有2个,(0.750,0.833]中有3个),即每层的样本点都无法保证达到最大程度的分层均匀性。
1.4 分层拉丁超立方体抽样的性质
为讨论抽样方法的性质,给出如下抽样方法优劣的定义。
定义4:若在抽样方法甲下比在抽样方法乙下得到的μ的估计量方差更小,则称抽样方法甲优于抽样方法乙。
比如,STRS优于SRS[9],即与SRS相比,基于STRS得到的μ的估计量的方差更小。本文将从理论上阐述STLHS相较于STRS在估计μ时所带来的改进。
假设分层随机抽样中的层数与分层拉丁超立方体抽样中的层数是相同的,记为s,设第c层积分值为μc,且利用式(2)得到的μc的估计量为̂c,则μ的估计量为:
其中,0<λc<1为权重,且=1。关于权重λc的选择,可采用等比例分配、最优分配、奈曼最优分配等原则确定。特别地,如果将每层样本看作同等重要,那么也可以令λ1=λ2=…=λs=1/s。若分别采用STRS和STLHS两种方法获取样本点来估计μ的值,有以下结论:
定理1:记̂STLHS为采用STLHS方法获取样本点对μ的估计量,则̂STLHS是μ的无偏估计量。
由于利用分层抽样得到的μ的估计量是无偏的[9],因此定理1的证明是显然的。为了给出进一步的结论,先介绍引理[10]。
引理1:若函数f()x在每一维变量xj(j=1,2,…,q)上均具有单调性,则LHS优于SRS,即VLHS(̂)≤VSRS(̂),其中,VLHS(̂)与VSRS(̂)分别表示在LHS与SRS下得到的μ̂的方差。
在引理1的基础上,有如下结论:
定理2:若每一层中对应的响应函数fc(x)(c=1,2,…,s)关于x均具有单调性,则利用式(8)估计μ时,STLHS优于STRS。
证明:根据STRS与STLHS的定义可知,STRS中每一层的样本是采用SRS得到的,而STLHS中每一层的抽样方法属于LHS。因此,基于引理1的结论,在定理2的条件下,利用第c层中的样本估计时,LHS优于SRS,即:
由式(8)可知:
即STLHS优于STRS。
2 数值模拟
本文通过一个例子对定理2的结论进行数值模拟验证。为了比较方便,不妨假设各层具有相同的样本量n,且λ1=λ2=…=λs=1/s。
例3:设f(x)=lnx为定义在区间(0,1]上的响应函数,X为在(0,1]上均匀分布的随机变量,计算f(x)在(0,]1的积分值为:
下面分别采用STLHS与STRS两种抽样方法获取样本对μ进行估计,以验证定理2的结论。为了简便,只比较层数s为2,每层样本量n均为5、10、20与50的四种组合下的情况。在每种组合下,重复抽样10000次,每次得到样本后均利用式(8)计算μ的估计量,其中,,模拟结果在表1中给出。

表1 两种抽样方法的估计量及其估计方差
从表1不难看出,在四种参数组合下,STLHS下得到的估计方差总是小于STRS下得到的估计方差,即STLHS优于STRS,这就验证了定理2的结论。此外,在两种抽样方法下,随着样本量的增加,估计方差都有下降的趋势,这也与常识相符。
3 结束语
本文基于拉丁超立方体抽样在估计总体均值时优于简单随机抽样的事实,对分层随机抽样进行了改进,提出了分层拉丁超立方体抽样的概念,给出了两种抽样算法。此外,不仅从理论上证明了在估计总体均值方面,若被积函数满足单调性时,则分层拉丁超立方体抽样优于分层随机抽样,还利用数值模拟对理论结果进行了验证。本文的结果为蒙特卡罗方法估计高难度积分提供了很好的抽样方法。值得指出的是,本文仅针对一维情形给出了抽样算法,即只有一个分层变量情形。对于包含两个或两个以上分层变量的情形,若每一维的分层变量是独立的,则可以基于本文的算法1或算法2在每一维进行独立抽样,从而获得所需样本;而对于分层变量不独立的情形,并不能基于一维结果进行简单推广,这也是接下来值得研究的问题。此外,式(8)中权重λc的选择也是值得探索的问题。

