蔬菜移栽机斜齿轮-非圆齿轮行星轮系取苗机构研究

周海丽 刘建刚 俞高红 齐 鹏 王 磊 郑 剑

(1.浙江理工大学机械工程学院, 杭州 310018; 2.浙江省种植装备技术重点实验室, 杭州 310018;3.武夷学院机电工程学院, 南平 354300; 4.杭州杭氧透平机械有限公司, 杭州 310011)

0 引言

取苗机构是移栽机械实现自动移栽的关键核心零部件,国内外学者在取苗机构的研究方面取得了一定的进展,主要采用各种杆结构或PLC控制取苗的方式实现自动移栽取苗。相比各种杆机构,轮系取苗机构工作平稳,其对称旋转式分布旋转一周可以实现两次取苗和推苗动作,取苗效率高,学者也开展了大量研究[1-18]。

这些研究中,轮系取苗机构主要采用不完全的非圆齿轮实现间隙传动,而不完全的非圆齿轮传动不可避免存在一定冲击;部分机构采用完全非圆齿轮连续传动提高传动平稳性,但其推苗角还可进一步优化(增大推苗角可提高推苗时秧苗的直立度,提高成功率)。因此,设计一种完全非圆齿轮行星轮系取苗机构且进一步优化推苗角是轮系取苗机构提高取苗效率行之有效的方法。

非圆齿轮行星轮系取苗机构的运动特性取决于总传动比曲线和中心距。根据课题组前期的研究[19-23],传动比满足二次不等幅传动,可更好地调整和设计较优取苗轨迹。然而,前期提出的传动比曲线多采用样条函数对原始传动比数据进行拟合,这种拟合方法没有具体的传动比数学模型,无法获得传动比曲线设计参数对取苗机构取苗轨迹、取苗特性和传动比曲线的变化关系。

本文根据蔬菜自动移栽机取苗要求,提出一种新型行星轮系取苗机构,即一级传动采用完全非圆齿轮、二级传动采用斜齿轮(传动比1∶1,增大重合度的方法);利用傅里叶函数初步设计机构二次不等幅传动比曲线,分析傅里叶函数系数(对应不同传动比曲线)对取苗机构取苗轨迹、传动特性、取苗角和推苗角影响的变化规律;基于人机交互设计方法获得满足取苗工作要求的傅里叶系数组合,由此设计一种具有较大推苗角的取苗机构,最后通过取苗试验验证该取苗机构设计的可行性。

1 取苗机构设计

1.1 取苗机构设计要求

根据蔬菜自动移栽机取苗要求,提出一种非圆齿轮行星轮系取苗机构,其设计目标为:取苗臂秧针为了能与秧箱配合,取苗角一般为35°～50°;为保持钵苗能直立下落到投苗位置,推苗角一般为60°～90°;为保证全程取苗臂之间不会发生干涉,取苗臂间距一般大于5 mm;为保证取出的钵苗基质的完整性,尖嘴宽度一般小于10 mm;入钵角过小或过大,易出现与钵盘或钵苗叶子及主体发生干涉,伤害钵苗,入钵角度一般为10°～30°;出钵角过大,秧针夹紧钵苗后在钵盘内向上运动,导致钵苗基质与钵盘碰撞挤压,伤害钵苗根系以及钵盘,出钵角度一般小于55°;取苗深度为35 mm。

1.2 基于傅里叶函数的传动比曲线初步拟合设计

设计较大推苗角可以改善推苗效果,从而提高取苗机构的推苗成功率。同时,秧针取苗入钵和出钵时尽量保持直进直出,更有利于秧针入钵取苗。因此,设计取苗轨迹,应同时考虑推苗角和取苗角,从而综合提高取苗效果。

非圆齿轮行星轮系取苗机构传动比需满足二次不等幅传动[23]。利用傅里叶函数,初步设计一条如图1所示的二次不等幅传动比曲线[24],实现传动比曲线设计参数的量化表达。通过调整傅里叶函数系数(傅里叶系数)改变传动比曲线,并分析不同系数下的取苗轨迹以及从动轮和秧针的运动特性,进而实现取苗轨迹、取苗角和推苗角的合理设计。傅里叶函数公式为

图1 传动比曲线Fig.1 Transmission ratio curve

(1)

式中an、bn、c0、w——傅里叶函数系数

θ——主动轮角位移

从动轮角位移θc计算公式为

(2)

1.3 取苗机构设计方案

根据图1传动比曲线,设计如图2所示的行星轮系取苗机构,一级传动采用非圆齿轮,二级传动采用标准斜齿轮传动(传动比为1∶1)。非圆的太阳轮固定在机架上与第1级中间非圆齿轮啮合,第2级中间标准斜齿轮与斜齿轮行星轮啮合,中间非圆齿轮和中间斜齿轮相互固定,取苗臂与二级行星轮固定,取苗臂秧针实现所需的取苗轨迹。行星架围绕旋转中心点O顺时针旋转,带动第1和第2级中间轮与行星轮在啮合传动的同时分别围绕旋转中心O1、O2进行自转。在1个周期内,2个取苗臂沿取苗轨迹共取苗2次。钵盘一般45°放置。在轨迹A-B-C段,取苗臂完成取苗过程;在轨迹C-D段,取苗臂完成持苗过程;在轨迹D-E段,取苗臂完成推苗过程;在取苗轨迹E-A段,取苗臂完成一个周期的取苗过程,回程准备下一周期的取苗。取苗角和推苗角分别如图2中δ和ζ所示。

图2 取苗机构简图Fig.2 Schematic of seedling picking mechanism1.太阳轮 2.行星架 3.中间斜齿轮 4.行星斜齿轮轮 5.取苗臂 6.非圆中间轮 7.取苗轨迹 8.钵盘

2 取苗机构运动学分析

行星轮系取苗机构设计方案和传动原理如图2所示,对各回转中心的坐标和速度等运动学参数进行理论计算。

中间轮旋转中心O1位移方程为

(3)

式中L1——第1级齿轮中心距,mm

φ0——行星架初始安装角位移,rad

φ1——行星架角位移,rad

行星轮旋转中心O2位移方程为

(4)

式中L2——第2级齿轮中心距,mm

δ0——第2级齿轮中心线相对于第1级齿轮中心线的角位移,rad

取苗臂秧针尖点Q位移方程为

(5)

其中

式中S——行星轮旋转中心到秧针尖点距离,mm

φ2——行星轮相对行星架角位移 (由于2级传动为斜齿轮等比传动),rad

β0——取苗臂相对于行星架的初始安装角位移,rad

取苗臂秧针尖点Q速度方程为

(6)

3 傅里叶函数系数对取苗机构运动特性影响分析

根据取苗机构的设计目标及给定的初始传动比曲线,给定中心距L1=L2=60 mm。

开发人机交互式软件,调节取苗机构设计目标的参数直至获得一组适合蔬菜取苗的取苗轨迹非劣解,并开展取苗机构结构设计。如图3所示为软件开发流程图,设计的软件界面如图4所示。

图3 软件开发流程图Fig.3 Software development flowchart

图4 取苗机构设计软件界面Fig.4 Software interface for seedling picking mechanism design

通过分析可知,随系数i的增大,傅里叶系数ai和bi(i=1,2,…,8)对取苗轨迹的影响逐渐降低。本文仅列举分析前3组系数对取苗轨迹及取苗机构传动特性的变化关系,分别分析传动比曲线的傅里叶系数c0、a1、b1、a2、b2、a3、b3及w对取苗轨迹、传动比曲线、从动轮角位移、角速度(从动轮角位移和角速度影响非圆齿轮传动的平稳性)及秧针尖点的速度(秧针尖点的速度影响秧针取苗和推苗的稳定性)传动特性,如图5～14所示。

图5 系数c0对取苗机构运动特性参数影响的变化规律Fig.5 Variation law of c0 coefficient on motion characteristic parameters of seedling picking mechanism

傅里叶系数c0、w对取苗机构运动特性的影响如图5、6所示。由图5可知,随着系数c0的增大,传动比的2个波峰下降,且传动比曲线与横坐标轴的面积减小(小于2π);取苗轨迹的环扣由大变小至消失,并出现反向增大的环扣;从动轮角位移存在变小的趋势;从动轮角速度减小;秧针尖点x方向的速度整体减小;秧针尖点y方向的速度整体增大。由图6可知,随着系数w的增大,传动比的2个波峰提前向左移动出现,取苗轨迹变小,从动轮角位移呈现变小的趋势,从动轮角速度向左偏移,秧针尖点x方向的速度整体减小,秧针尖点y方向的速度整体增大。

图6 系数w对取苗机构运动特性参数影响的变化规律Fig.6 Variation law of w coefficient on motion characteristic parameters of seedling picking mechanism

傅里叶系数a1、b1对取苗机构运动特性的影响如图7、8所示。由图7可知,随a1的增大,传动比曲线第1波峰先增大后减小,第2波峰整体减小;取苗轨迹变化很大;从动轮角位移减小;从动轮角速度增大;秧针尖点x方向速度减小;秧针尖点y方向速度增大。在取苗机构设计时,对传动比曲线的设计,应合理调试系数a1,避免对取苗轨迹产生较大的变化。由图8可知,随系数b1的增大,传动比曲线第1波峰值整体增大,第2波峰值整体减小;取苗轨迹整体变小;从动轮角位移减小;从动轮角速度减小;秧针尖点x方向速度减小;秧针尖点y方向速度增大。

图7 系数a1对取苗机构运动特性参数影响的变化规律Fig.7 Variation law of a1 coefficient on motion characteristic parameters of seedling picking mechanism

图8 系数b1对取苗机构运动特性参数影响的变化规律Fig.8 Variation law of b1 coefficient on motion characteristic parameters of seedling picking mechanism

傅里叶系数a2、b2对取苗机构运动特性的影响如图9、10所示。由图9可知,随a2系数增大,取苗轨迹及其取苗机构特性变化较为明显;传动比曲线的第1波峰出现先增大后减小,第2波峰增大;取苗轨迹影响较大;从动轮角位移减小明显;从动轮角速度前半个周期有明显波动,后半个周期变化不明显;秧针尖点x方向速度减小;秧针尖点y方向速度增大。在取苗机构设计时,对传动比曲线的设计,应合理调试系数a2,避免对取苗轨迹产生较大的变化。由图10可知,随系数b2的增大,传动比曲线的第1个波峰出现先增大后减小,第2波峰增大;取苗轨迹变大;从动轮角位移前半个周期变化明显,呈现减小趋势,后半个周期变化不明显;从动轮角速度增大;秧针尖点x方向速度前部分减小明显;秧针尖点y方向速度增大。

图9 系数a2对取苗机构运动特性参数影响的变化规律Fig.9 Variation law of a2 coefficient on motion characteristic parameters of seedling picking mechanism

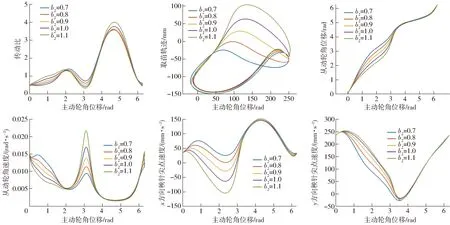
图10 系数b2对取苗机构运动特性参数影响的变化规律Fig.10 Variation law of b2 coefficient on motion characteristic parameters of seedling picking mechanism

傅里叶系数a3、b3对取苗机构运动特性的影响如图11、12所示。由图11可知,随系数a3变化,取苗轨迹、取苗机构特性、从动轮角位移、从动轮角速度变化不明显;在传动比曲线及取苗机构的设计时,系数a3适合用于对取苗轨迹进行微调。

图11 系数a3对取苗机构运动特性参数影响的变化规律Fig.11 Variation law of a3 coefficient on motion characteristic parameters of seedling picking mechanism

由图12可知,随系数b3的增大,传动比曲线整体减小;取苗轨迹环扣先减小后增大;从动轮角位移和角速度前半个周期波动较大,后半个周期变化不明显;取苗臂秧针尖点x方向的速度前半周期变化明显,后半周期变化整体增大;秧针尖点y方向速度变化不明显。

图12 系数b3对取苗机构运动特性参数影响的变化规律Fig.12 Variation law of b3 coefficient on motion characteristic parameters of seedling picking mechanism

4 傅里叶函数系数对取苗和推苗角影响分析

取苗角和推苗角是取苗机构设计的关键因素,其大小影响取苗机构取苗成功率,增大推苗角可以提高推苗时秧苗的直立度,使其能够顺利落入植苗机构,从而提高推苗效果。因此,有必要研究传动比曲线设计的傅里叶系数对取苗机构的取苗角和推苗角的影响。

傅里叶系数对取苗角和推苗角的变化规律如图13、14所示。由图13可知,系数b1和b3与取苗角呈负相关;随b2增大,取苗角出现最小值31.06°;取苗角随其余参数的增大而增大。由图14可知,随傅里叶系数(w、c0、b2、b3)的增大,推苗角会出现拐点,其中w和c0出现最大值90°,b2和b3出现最小值分别为78.5°和78.4°,推苗角随其余参数的增大而减小。

图14 傅里叶系数对推苗角的影响Fig.14 Effect of Fourier coefficient on seedling pushing angle

通过人机交互的设计方法获得一条满足取苗工作要求的取苗轨迹对应的傅里叶系数:c0=1.209,a1=-1.094,b1=-0.282 1,a2=0.142 8,b2=0.934 9,a3=0.062 85,b3=-0.432 1,a4=0.055 52,b4=0.186,a5=0.005 833,b5=0.053 68,a6=0.070 99,b6=-0.027 09,a7=0.005 129,b7=-0.037 21,a8=0.001 705,b8=-0.011 66,w=0.786 3。最终设计的取苗机构主要参数为:S=152 mm,φ0=64°,β0=11°,δ0=62°,L1=L2=60 mm。设计的取苗机构三维图如图15a所示。利用虚拟仿真软件对取苗机构进行三维仿真,仿真轨迹和理论轨迹对比如图15b所示。

对取苗机构进行运动学计算,对比取苗臂秧针尖点Q的位移和速度曲线理论和仿真结果的一致性。由图16可知,秧针尖点Q的x、y方向位置坐标仿真值与理论值一致,x、y方向速度仿真值和理论值基本一致。可见秧针尖点Q的运动学参数仿真值与理论值吻合,证明了该取苗机构的设计是可行的。

图16 点Q运动学参数Fig.16 Kinematics parameters of Q point

5 取苗机构试验

5.1 取苗机构空转试验

根据取苗机构设计参数,制造并装配取苗机构,实物装配如图17a所示,取苗机构安装试验台进行空转试验如图17b所示。利用高速摄像技术描绘取苗轨迹如图17b所示,对比理论和仿真轨迹如图17c所示。由图17可知,取苗轨迹试验值与理论和仿真值基本一致,证明了该取苗机构设计的可行性。

图17 取苗机构实物装配图Fig.17 Physical assembly drawings of seedling picking mechanism

图18为行星轮系取苗机构的取苗角和推苗角的测量试验,利用倾角测量仪测量取苗机构在取苗和推苗时的角度,该取苗机构的取苗角和推苗角分别为45.5°、81.2°。取苗角和推苗角理论值和测试值的对比如表1所示,误差小于1.2%。

表1 取苗角和推苗角理论值和试验值对比Tab.1 Comparison between theoretical and experimental values of seedling angle and pushing angle

图18 取苗机构取苗角和推苗角测试试验Fig.18 Test experiment on seedling picking angle and pushing angle of seedling picking mechanism

5.2 取苗机构台架取苗试验

为了验证非圆齿轮行星轮系取苗机构取苗效果,利用西兰花钵苗开展取苗机构取苗试验,如图19所示,试验参数为:每一盘穴盘含西兰花钵苗100株,开展取苗机构不同转速(40～60 r/min)的取苗试验,取苗结果如表2所示。

表2 取苗试验结果Tab.2 Seedling extraction experiment

图19 取苗机构取苗试验Fig.19 Seedling picking test of seedling picking mechanism

由图19和表2可知,该取苗机构取苗成功率较好,在转速40、50、60 r/min时取苗成功率分别为94%、90%、88%。取苗失败的主要原因是钵苗叶子的杂序生长,导致在取苗夹紧阶段,钵苗叶子卡进推苗爪和取苗臂壳体的缝隙中,发生夹带和茎叶相互缠绕。取苗试验进一步验证了取苗机构设计的可行性。

6 结论

(1)基于傅里叶函数设计了一种二次不等幅传动比曲线,分析了傅里叶函数系数对传动比曲线、取苗轨迹、从动轮和秧针尖点速度特性及推苗角和取苗角的影响规律。

(2)根据传动关系,采用人机交互设计了一种具有较大推苗角的非圆齿轮行星轮系取苗机构,并采用虚拟仿真对取苗机构进行了运动学分析,证明了机构设计的可行性。

(3)制造和装配取苗机构,通过取苗轨迹、推苗角、取苗角对比验证了试验结果与理论结果的一致性。对取苗机构进行转速40、50、60 r/min的台架取苗试验,得出取苗机构的取苗成功率分别为94%、90%、88%。