隧道爆破振动在地层中的传播规律分析
1 引言
隧道施工中掌子面爆破会对邻近地表既有建筑物和已有的地下交通建筑物结构产生不利影响, 为有效控制爆破振动的影响,许多学者对爆破振动传播规律进行研究。罗阳等[1]利用ANSYS 进行小净距隧道爆破振动的数值模拟,得出振速不仅随着净距的增大而增大,而且跟装药量成正比。 陈沛等[2]依托武汉地铁5 号线爆破项目, 利用ANSYS-Lsdyna 平台对地铁隧道掏槽眼延时爆破进行模拟, 得出随着掏槽眼延时时间的增加爆破对既有建筑物的振动逐渐减小。吴波等[3]通过FLAC 3D 模拟隧道爆破对既有建筑物的影响, 得出迎爆侧衬砌拱腰处的振动速度最大。宋战平等[4]通过数值模拟和非线性模糊层次分析相结合的方法, 得出邻近既有建筑物时隧道爆破方案优化的新方法。 王秋懿[5]通过Lsdyna 模拟交叉隧道掌子面爆破的振动, 研究隧道支护结构在受到邻近隧道施工爆破影响下的振动规律。于建新等[6]对大断面隧道爆破监测数据进行分析,研究不同爆炸设计参数下的振动规律。 单仁亮等[7]基于现场爆破监测数据,研究不同炮眼的爆破振动传播规律。季相臣等[8]基于贵阳某隧道项目,研究大断面小净距隧道爆破时掌子面前方振动传播规律。张业伟[9]通过现场爆破试验对施工阶段爆破振动的控制技术进行研究。
从以上学者的研究可以看出, 目前对隧道爆破邻近既有建筑物方面的振动规律的研究较少, 本文依托安六高铁地宗隧道进行爆破试验,对爆破振动的传播进行研究,基于回归分析确定爆破参数,得出爆破振动衰减公式,并将该公式用于地宗隧道爆破方案的设计,优化了爆破参数。
2 工程概况
地宗隧道进口里程桩号为DK41+720, 出口里程桩号为DK44+765,全长3 045 m,最小埋深约12 m,地表居民密集,隧道爆破施工引起的地震效应过大会影响居民的安全生活和建筑物的安全使用。 隧道与建筑物位置关系示意图如图1 所示。
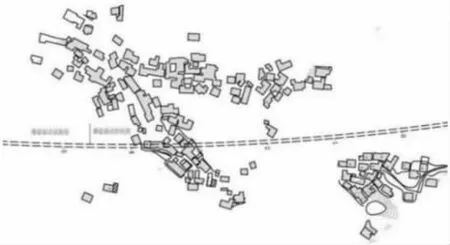
图1 隧道与建筑物位置关系示意图
隧道位于六枝向斜南翼,自然坡度20°~60°,局部陡立。隧址区穿越构造低中山区,相对高差290 m。 隧道纵断面图如图2 所示。
3 爆破试验方案
3.1 试验监测仪器
爆破测振仪应具备以下功能:可靠的自动触发装置;可以设置负延时记录;可以收集垂向、径向、纬向的振速和频率;采样频率要远高于测试信号;基于以上要求,选取TC-4850 爆破测振仪。
3.2 试验测点布置
试验测点布置的合理性对爆破振动监测结果的准确性起到很重要的作用,本文主要研究爆破振动的传播规律,测点应针对研究对象在关键位置进行布点,因此,选取DK42+430 为爆破试验掌子面,在距离爆心30 m、33 m、37 m、53 m、67 m 布置监测仪器,测点布置如图3 所示。
3.3 试验爆破方案
隧道采取两台阶法施工, 上台阶单循环开挖进尺2.4 m,基于现场的地质条件,隧道爆破采用光面爆破,周边眼间距为60 cm,掏槽眼竖向间距为20 cm,底板眼间距为100 cm,炮孔布置如图4 所示。
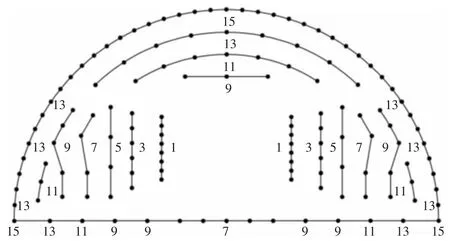
图4 炮孔布置图(单位:cm)
3.4 爆破试验结果
试验段共布置5 个测点, 对两次爆破在地层中引起的垂直方向(垂向)、隧道轴向(径向)、水平切向(切向)的振速和频率进行监测,监测数据如表1 所示。 为了准确地呈现爆破振动在地层的传播规律, 将两次监测数据的平均值作为该测点的数据进行分析。
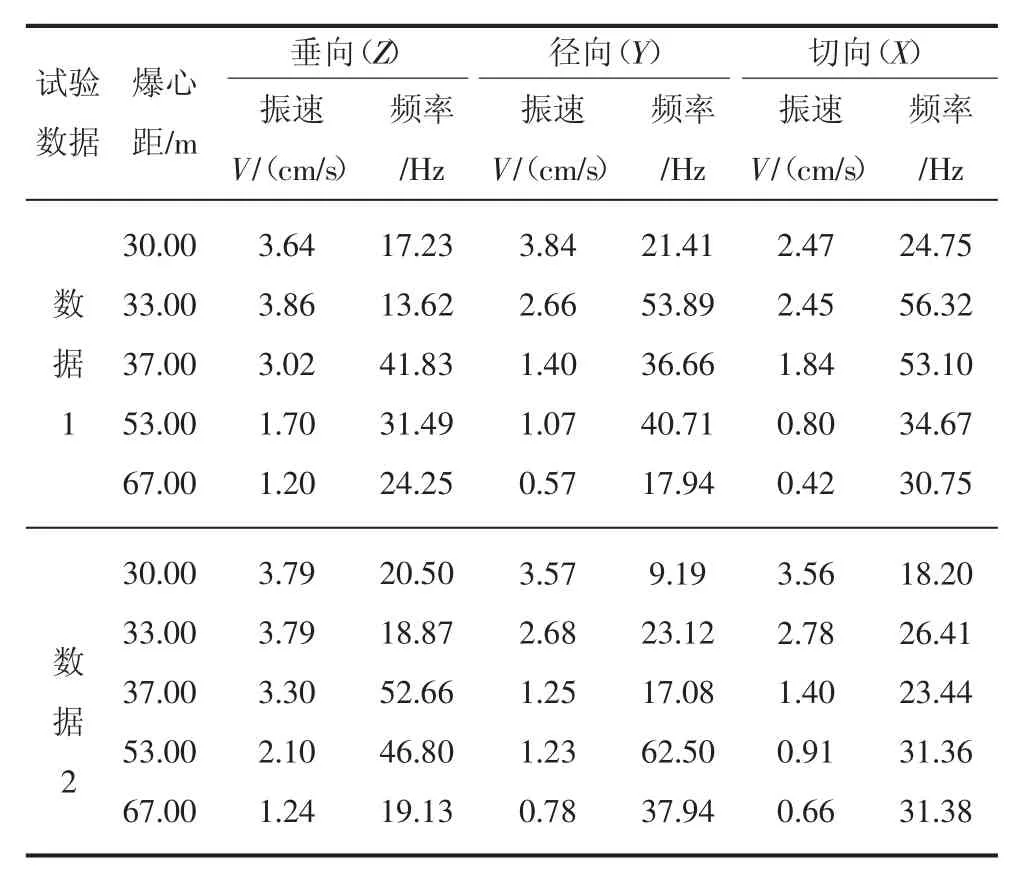
表1 爆破试验监测数据
4 试验数据分析
4.1 振动速度分析
图5 是地层中不同方向的爆破振动速度曲线, 从图5 可以看出, 振速在3 个方向上均呈现出随着爆心距的增大而逐渐减小,同时可以发现3 个方向振速中垂向最大。 振速变化曲线在爆破近区测点与测点间的斜率大于爆破远区, 这表明在爆破近区振速降低的速度大于爆破远区, 符合现场实际的爆破传播规律。
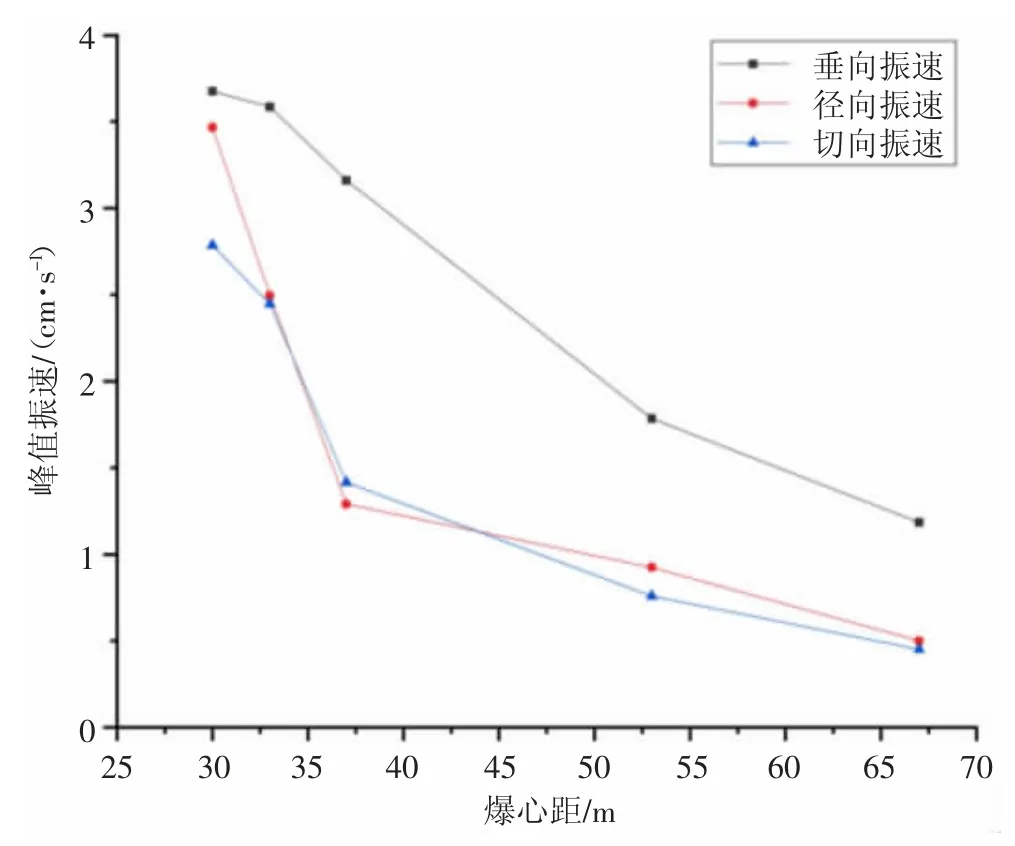
图5 爆破振速曲线
4.2 振动频率分析
图6 是测点振动频率随爆心距变化曲线图,由图6 可知,爆破振动频率在地层中3 个方向上均表现为“单峰”状态,即频率迅速增加然后逐渐减小的变化规律, 但与振速曲线相对比, 振动频率并没有表现出随着爆心距的增加严格衰减的趋势。
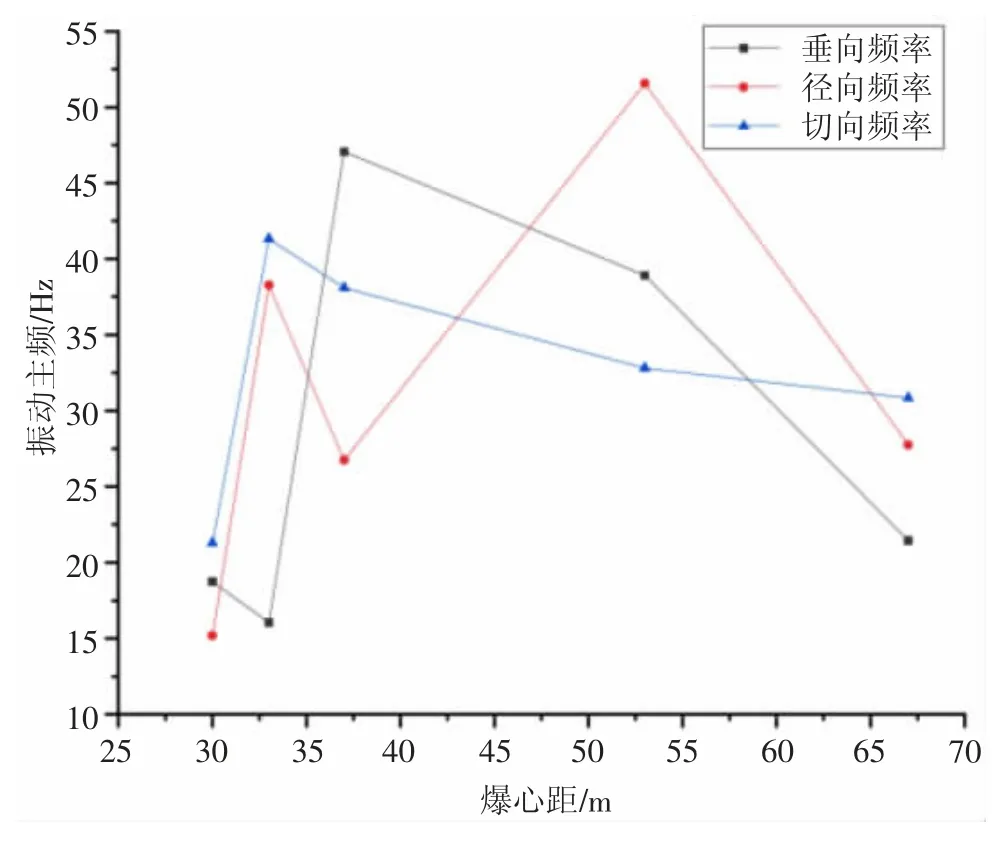
图6 爆破振动频率曲线
4.3 振速波形分析
图7 是测点振速时程图,VZ、VY、VX分别代表垂直方向、隧道轴向、水平切向3 个方向的振动速度。 从图7 可以发现,随着时间的变化测点振速呈现出迅速增大逐渐衰减的变化规律。 由图7 可知,由于0~200 ms 内隧道爆破装药量大,爆炸时临空面少,因此,该时间段爆破振速最大。在200~500 ms 段VZ方向振幅较小。 由于其余两个方向在传播途中有临空面,因此在3 个方向中VZ最大。
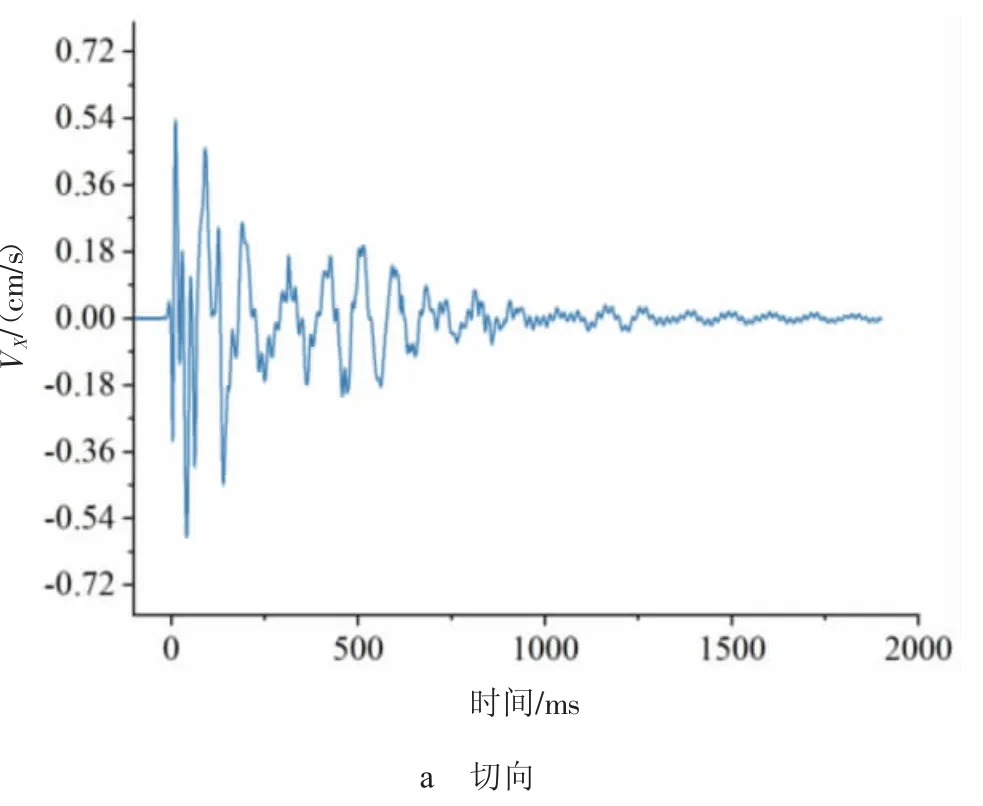
图7 振速时程曲线图
5 回归分析
由于不同围岩岩性差别很大, 采取经验参数确定的萨氏振动衰减公式,不能准确反映振动传播规律,对于计算爆破控振设计存在一定的误差。 因此,有必要基于现场的监测数据,进行回归分析,确定该场地段的K、α 值,从而得出该场地段的振动衰减公式。 最小二乘法时是一种非常有效且广泛使用的回归分析方法,其分析方法如下。
设监测获得数据:(x1,y1),(x2,y2),(x3,y3), …,(xn,yn),将监测数据采用一元线性回归方程进行拟合分析,方程如下:
因此,需采用最小二乘法确定k 和b 的值。
剩余误差的平方和ξ 最小是最小二乘法确定k 和b 的最终条件。
根据高等数学极限定理, 要使得ξ 最小必须满足以下条件:
其中:。
将振动衰减公式(7)转化为线性方程(8),根据现场爆破监测数据,基于最小二乘法,拟合得出场地相关系数k、α。 得出k 值为212.5,α 值为1.6471,其回归曲线如图8 所示。

图8 爆破数据最小二乘法回归曲线图
式中,V 为建筑物最大安全质点振速,cm/s;Q 为爆破最大单段药量,kg;R 爆破振动安全允许距离,m;k、α 为与场地条件有关的系数。
从图8 可以看出,得出的回归曲线具有较好的拟合效果,利用拟合推导爆破振动衰减公式是可行的, 将上述k、α 值代入式(7)获得该场地段的爆破振动衰减公式为:


图9 不同最大允许振速下的最大单段炸药量与爆心距关系图
6 结论
论文依托安六高铁地宗隧道项目,进行现场爆破试验。 对两次爆破在地层中引起的垂直方向(垂向)、隧道轴向(径向)、水平切向(切向)的振速和频率进行监测,基于试验数据进行爆破振动在地层中的传播规律研究。 得到以下结论:
1)通过振速、频率曲线图可以发现,振速在地层中不同方向呈现出随着爆心距的增大而逐渐减小, 同时可以发现3 个方向振速中垂向最大。 爆破振动频率在3 个方向上均表现为“单峰”状态,即频率迅速增加然后逐渐减小的变化规律。
2)通过测点振速时程图得出测点振速随着时间逐渐减小最终振动速度降为0, 同时发现垂向振速 (VZ) 比径向振速(VY)、切向振速(VX)衰减更快。
3)对监测数据采用最小二乘法进行回归分析,获得了试

